一维线性Klein-Gordon方程Neumann边值问题的高阶差分格式

盛秀兰郝宗艳吴宏伟

(1.东南大学数学学院,江苏南京 210096)

(2.江苏开放大学通识教育学院,江苏南京 210036)

1 引言

本文研究如下一维非线性Klein-Gordon方程Neumann的边值问题的数值解

其中α>0为常数,f(x,t),g(u)为满足相容性条件的光滑函数.

Klein-Gordon方程是相对论量子力学和量子场论中用于描述零自旋粒子的自由运动方程,关于它的数值解法已有不少研究结果.文献[1]基于样条基函数提出了一个数值格式;四阶紧格式在文献[2]中进行了研究;基于变分迭代法的数值格式及边界元方法可参见文献[3,4];在文献[5]中导出了以三层样条差分格式逼近非线性Klein-Gordon方程;无界域上的问题的数值研究可参见文献[6];文献[7]中提出了一个基于有限差分和匹配法的新的数值格式;而文献[8]提出了微分积分法.所有这些文献中的研究都是针对Dirichlet边界条件,对于Neumann边界条件下的高阶差分格式还没有很好的结果.近年来,具有Neumann边界条件的热方程的高阶差分格式已有一些研究结果如文献[9–11].文献[12]研究了Cahn-Hilliard方程Neumann边界条件下的三层线性化紧格式;文献[13]中建立了哈密尔顿非线性波方程Neumann边界条件下的高阶显格式,该方法空间方向基于紧格式,时间方向基于Runge-Kutta-Nystrom方法.通过分析以上文献,了解到Klein-Gordon方程Neumann边值问题的无条件稳定的高阶差分格式,目前还没有这方面的结果,其主要困难是边界点的处理.本文利用Klein-Gordon方程及边界条件可得到在边界处的三阶导数和五阶导数的函数值,从而建立边界点和内点处的两点和三点紧差分格式,构造一个紧格式,并证明差分格式关于时间2阶收敛,关于空间4阶收敛.

2 记号及引理

设问题(1.1)–(1.3)存在光滑解u,记Ω=[a,b]×[0,T],本文假设

H1:u∈C(4,3)(Ω),且存在常数C0,使∀(x,t)∈(Ω)有

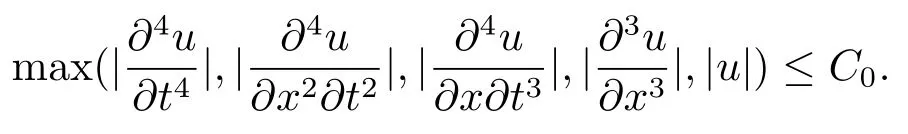
H2:函数g一阶可导,且存在正常数C,使得当|s|≤C0+1时,有

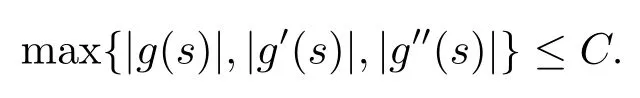
H3:∀(x,t)∈Ω,且存在常数C1,使.

由(1.1)式中的方程可得

将(2.1)式两边关于x的k(k=3,4,5)阶导数,且由边界条件(1.3)可得

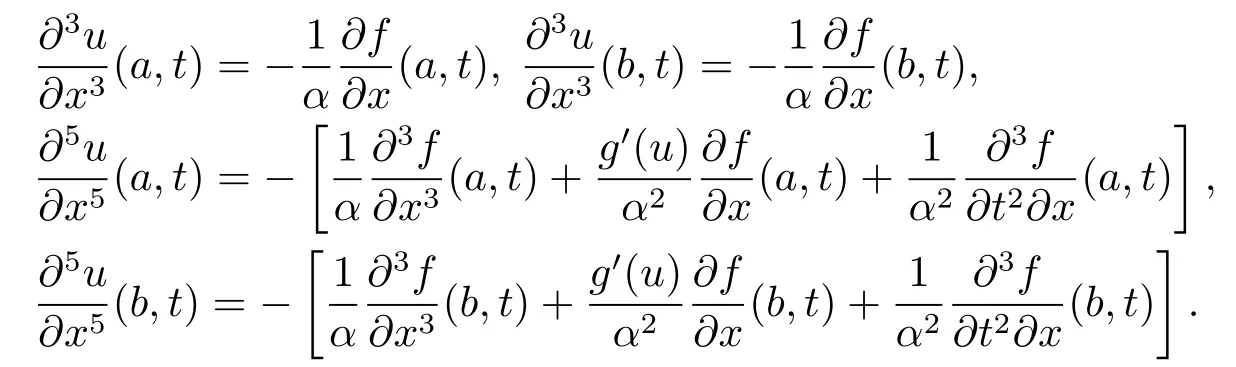
取正整数m,n,记空间和时间步长分别为,记x=a+ih,0≤i≤m,itk=kτ,0≤k≤n.定义

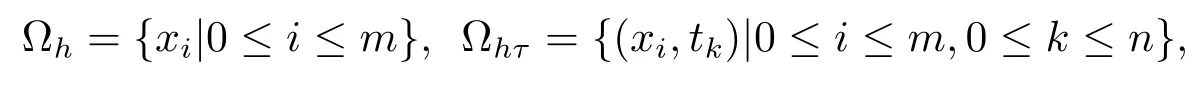
称(xi,tk)为节点,并设为Ωhτ上的网格函数,引进下面的记号

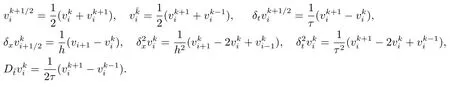
记Vh={v|v={vi|0≤i≤m}为Ωh上的网格函数},设v∈Vh,引进下列网格函数的模与半模

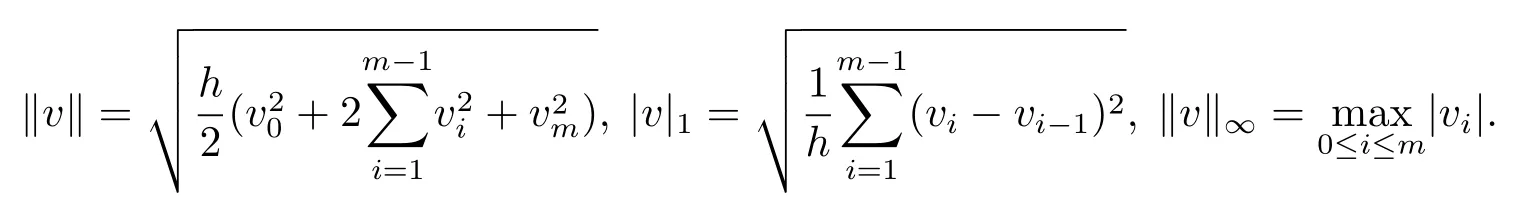
引理2.1[3]记ζ(s)=(1−s)3[5−3(1−s)2],s∈[0,1].

(1)若g(x)∈C6[x0,x1],则有

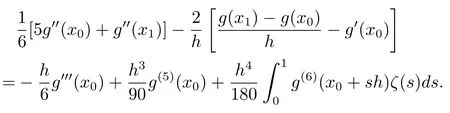
(2)若g(x)∈C6[xm−1,xm],则有

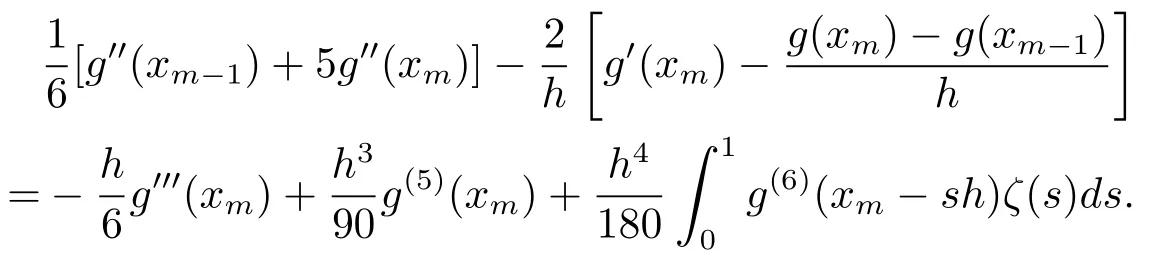
(3)若g(x)∈C6[xi−1,xi+1],1≤i≤m−1,则有

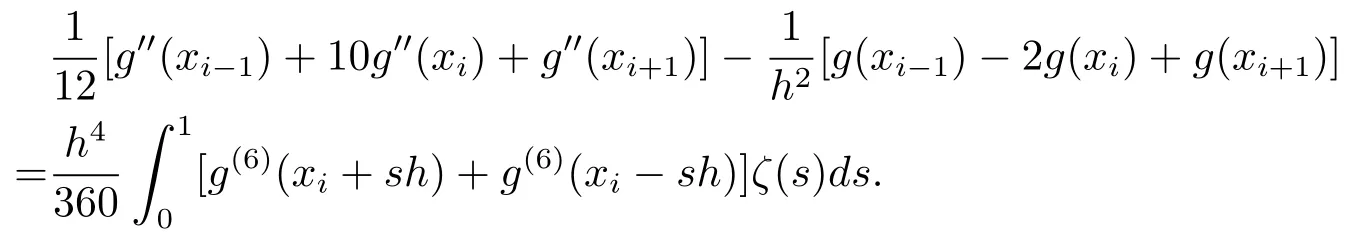
引理2.2[5]设v∈Vh,则有,且对任意ε>0,有

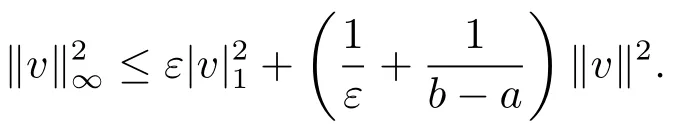
引理2.3[14]设h和c为两个常数,且h>0,若g(x)∈C2[c−h,c+h],则有

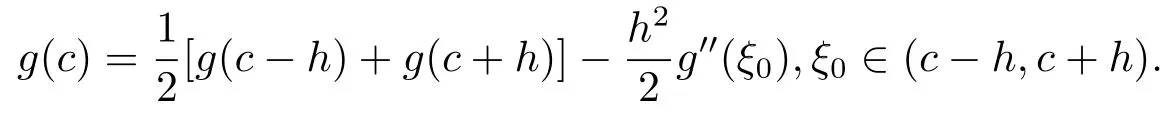
引理2.4[15]设为Ωhτ上的网格函数,则

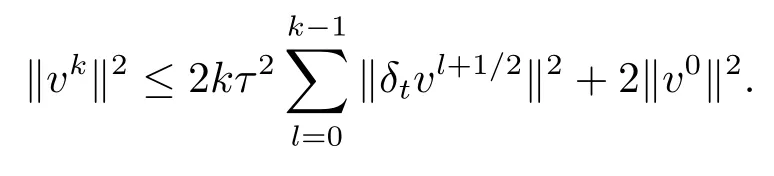
引理2.5设为Ωhτ上的网格函数,记

则当0≤k≤n−1时,有

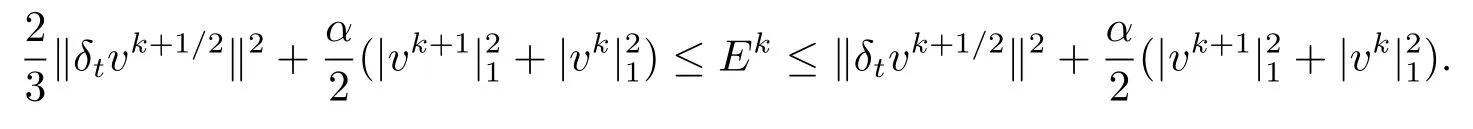
证由不等式

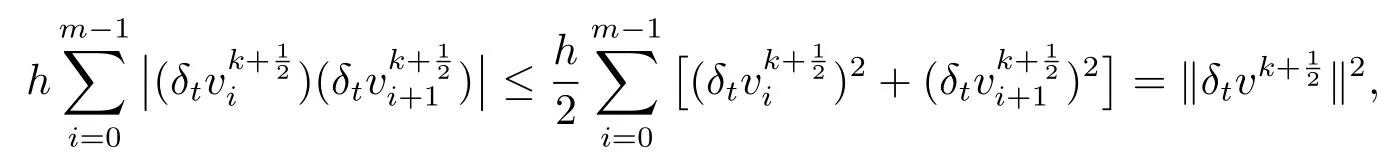
易得引理2.5.

3 差分格式的建立

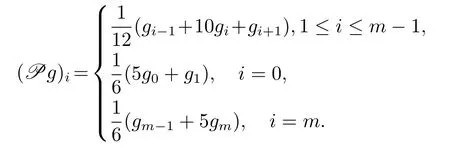
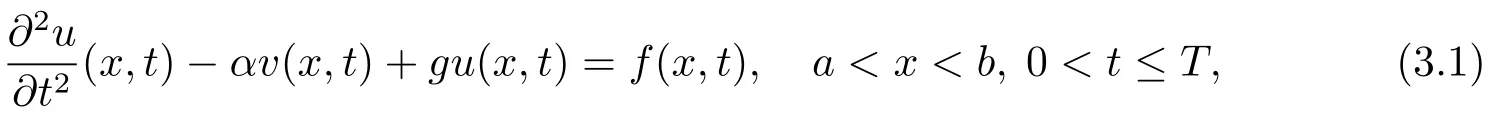
在结点(xi,tk)处考虑方程(3.1),并对两边作用算子P,且1≤i≤m−1,0≤k≤n−1,可得

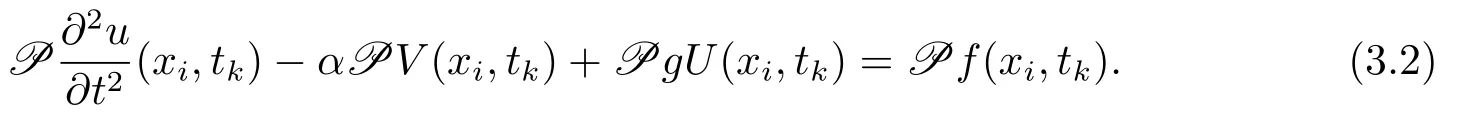
根据引理2.1,边界条件及作用算子P可得

由Taylor展开知

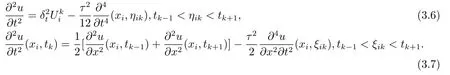
将(3.6)–(3.7)式带入到(3.2)式,且0≤i≤m−1,0≤k≤n−1,得到

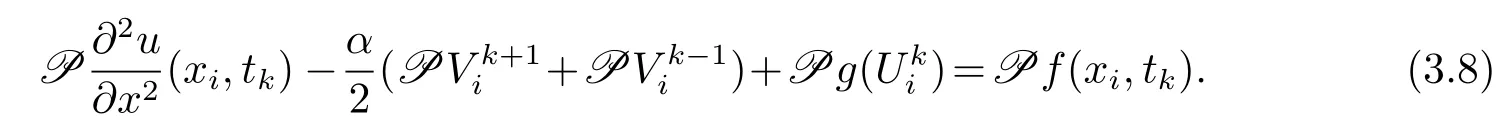
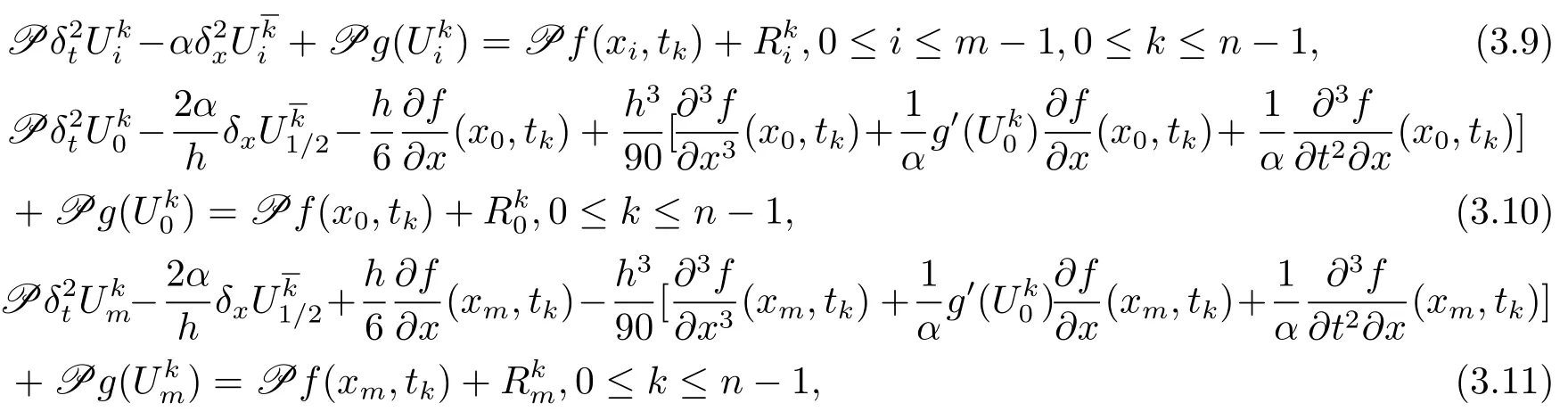
其中

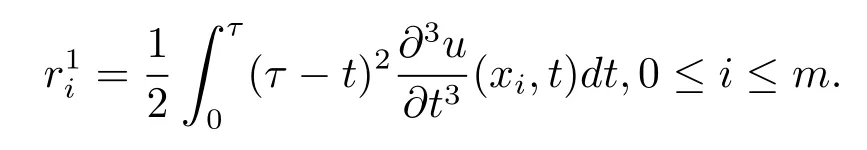
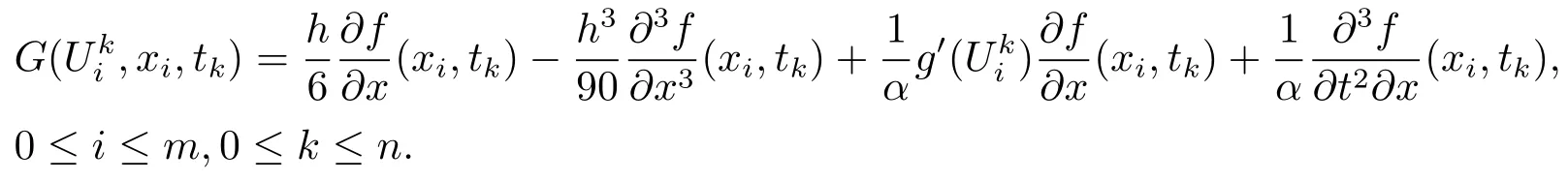
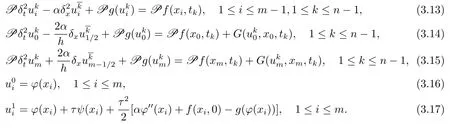
4 差分格式的收敛性

定理1设u(xi,tk)是问题(1.1)–(1.3)式的解,是差分格式的解(3.13)–(3.17)的解,记,则当时,有

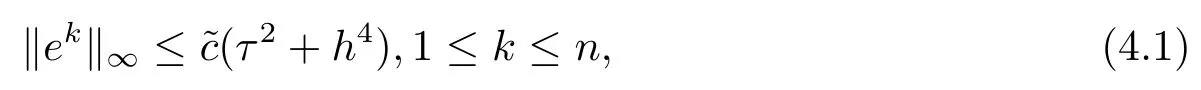
其中

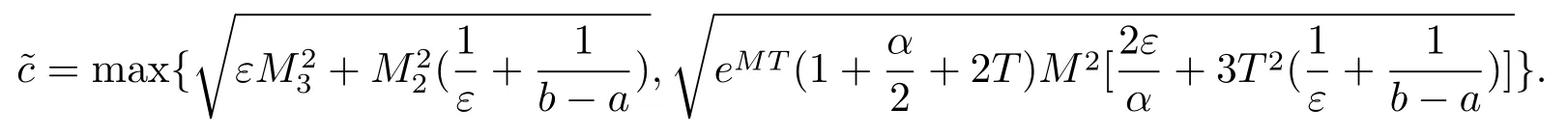
证将(3.9)–(3.12)式分别与(3.13)–(3.17)式相减,且1≤k≤n−1,得到误差方程

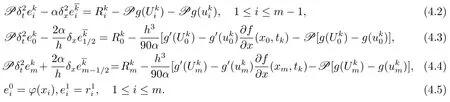
令

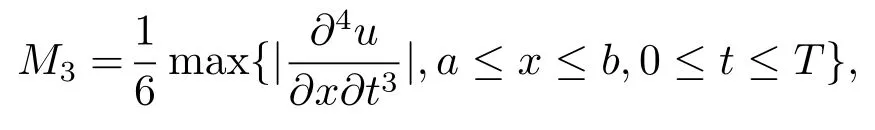
则有

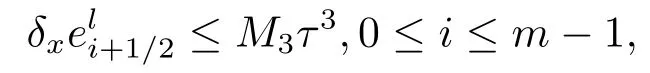
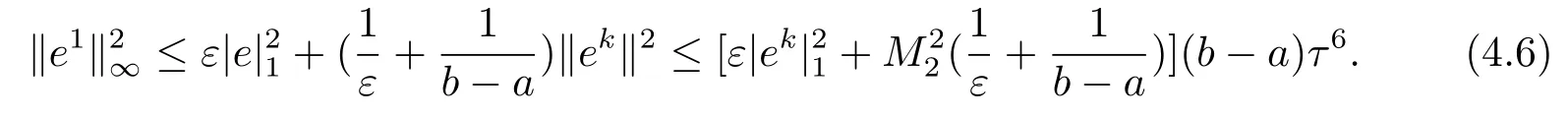
显然,(4.1)式对于k=1成立,现假设(4.1)式对于1≤k≤l成立,其中1≤l≤n−1.下面证明(4.2)式对k=l+1也成立,用,分别乘方程(4.2)–(4.4)三式,并关于i从1到m−1求和,且将三式相加可得J1+J2=J3,其中

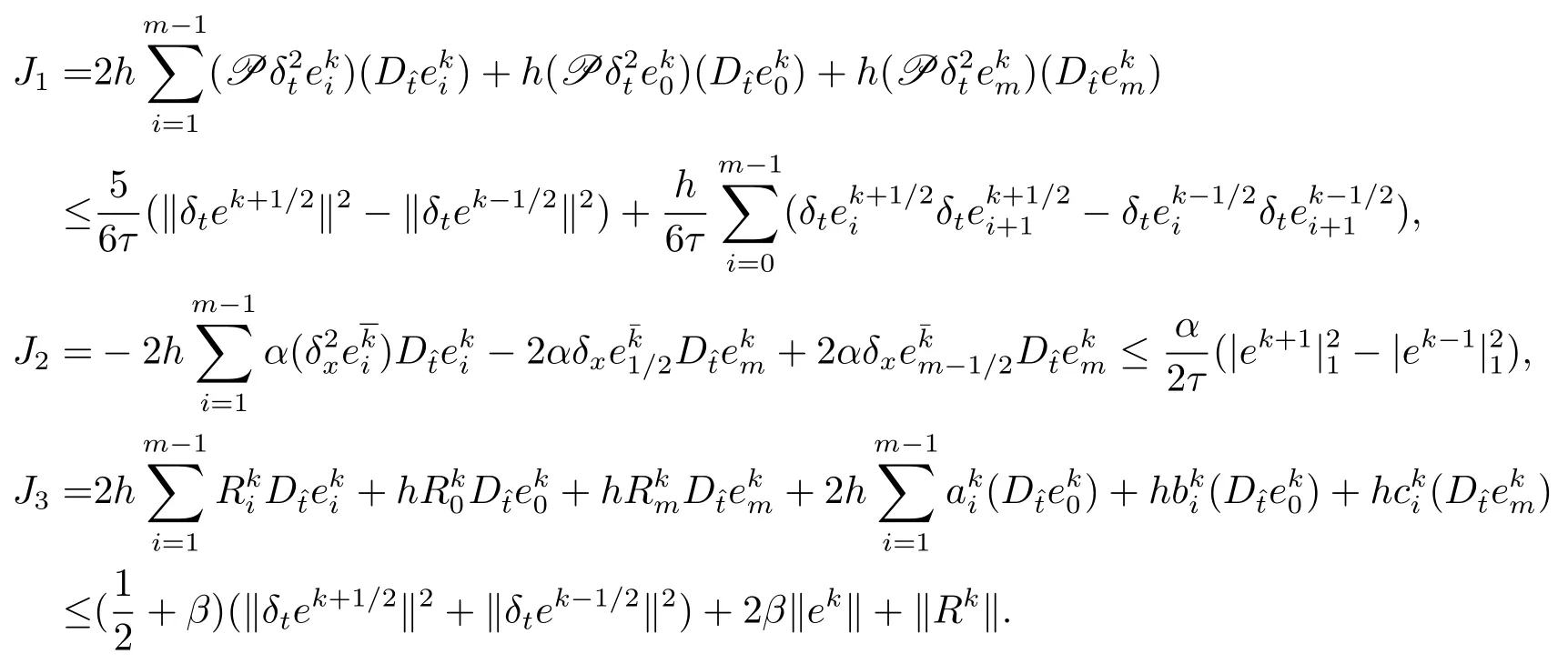
上述β为常数,其中如下

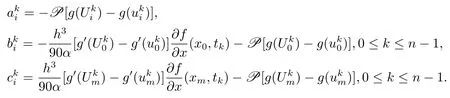
令

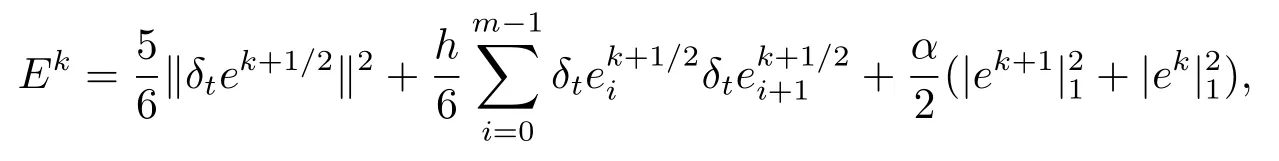
则J1+J2=J3可写为

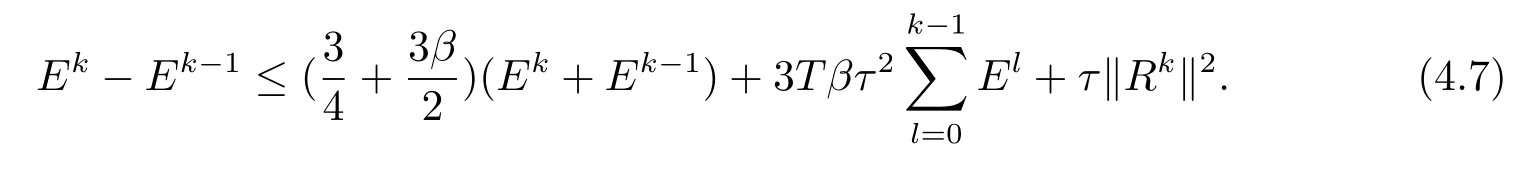
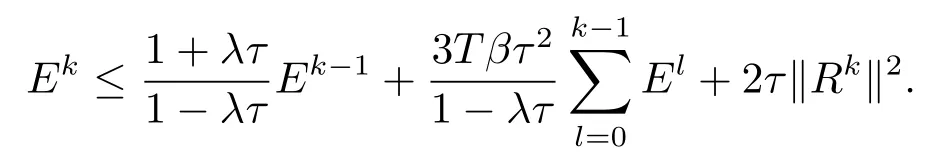
令Fk=max(Ek,Ek−1,Ek−2,···,E1,E0),则有

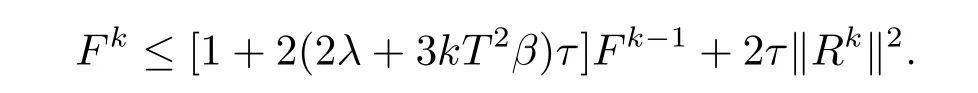
记M4=2(2λ+3kT2β),M4为正整数,故Fk≤(1+M4τ)Fk−1+2τkRkk2,由 Granwall不等式可得到

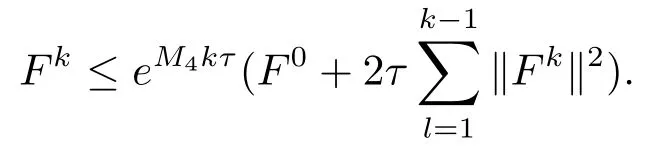
由Fk的定义可知F0=E0,则有

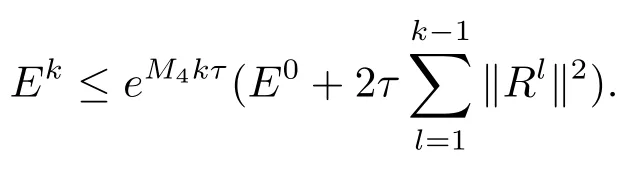
取M=max(M1,M2,M3,M4),并由引理2.5可得

由此可得

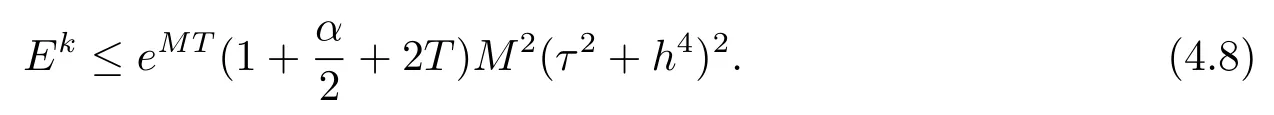
由引理2.4和引理2.5可知

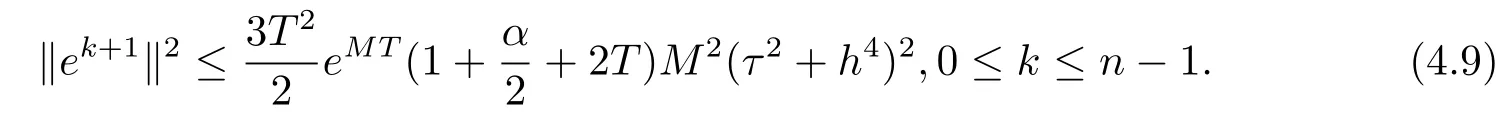
由(4.8)–(4.9)两式和引理2.2可知,对于任意的ε>0,有

5 差分格式的稳定性

类似讨论差分格式的收敛性可以得到差分格式(3.13)–(3.17)式关于初值的稳定性.

定理2设分别是差分格式(3.13)–(3.17)的解,记,假设条件H1,H2,H3成立,则当h,τ充分小时,且 1≤k≤n−1时,有

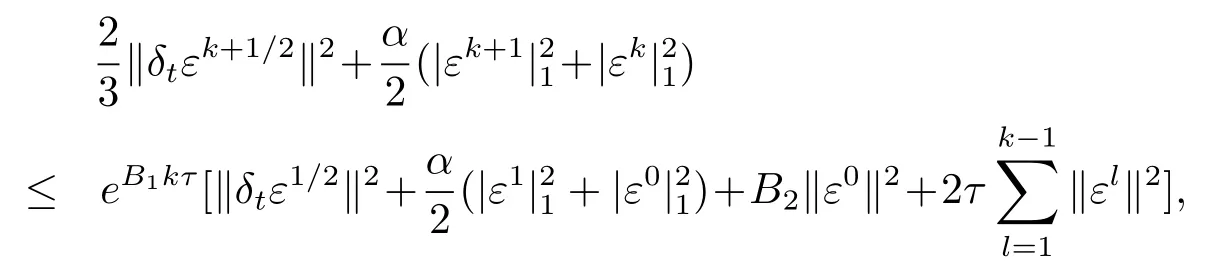
且B1,B2是与h,τ无关的正的常数,证明略.

6 数值试验

本节利用构造的差分格式(3.13)–(3.17)计算下面的定解问题

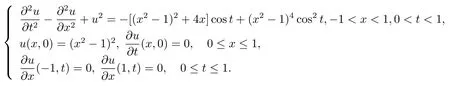
该问题的精确解为u(x,t)=(x2−1)2cost.计算结果见表6.1和表6.2.表6.1给出了在不同步长时某些节点处的误差,表6.2给出了不同步长时数值解的最大误差和误差比,其中

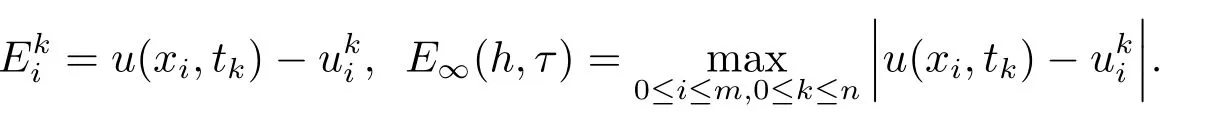
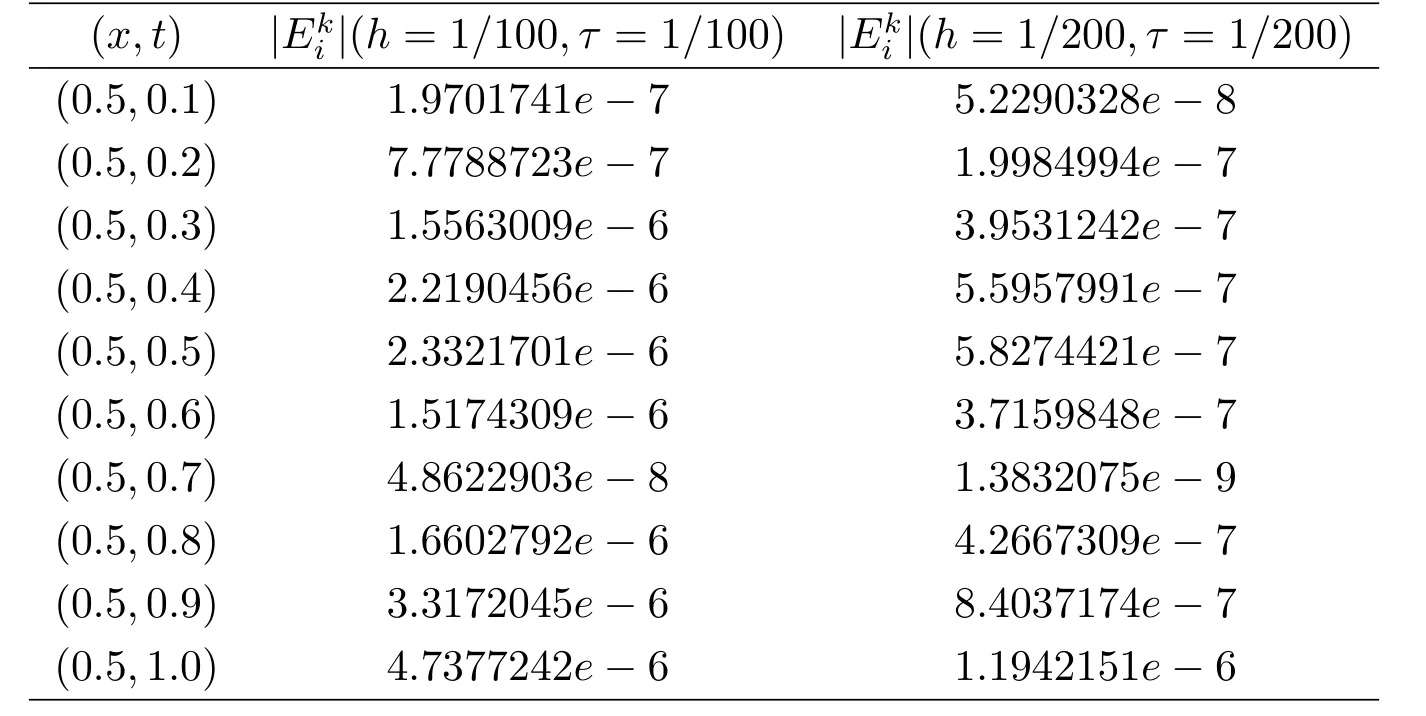
表6.1:部分结点处数值解的误差

表6.2:不同步长时数值解的最大误差和误差比

由表6.2可以看出,差分格式在无穷范数下的收敛阶为O(τ2+h4),这和理论分析结果一致.