温度变化对固支FGM输流管道横向振动的影响

郭 静，王忠民

(西安理工大学土木建筑工程学院，陕西西安710048)

管道是现代工业中最重要的一种载流装置，常见的管道系统有城市供水的长距离管线、大规模集中供暖系统、油田的长距离输油管线、核电站中的水循环系统等，这些管道系统对国民经济以及人民生活起着十分重要的作用。由于输流管道内的流体流动方式以及两端支撑条件的多样性，会导致管道产生横向复杂的动力学行为。流体流速越大，引起管道的振动越明显，甚至当流速超过某一临界值时，管道会发生屈曲失稳。同时，振动也是造成设备损坏、结构失稳、寿命减少等的主要原因，所以，为了提高管道系统的稳定性与安全性，输流管道动力学问题的研究得到越来越多学者的广泛关注。

2004年，Sarkar和Paidoussis[1]分析了悬臂梁、两端支撑的输流直管的流固耦合的振动机理。李宝辉[2]研究了管道固有频率、临界速度、临界压力与流体压力、流速、管道固支长度之间的关系。He[3]等利用线性和非线性热弹性理论分析了热载荷作用下简支输流管道的振动稳定性问题。宋日新[4]基于复合材料的细观力学方法，采用等应变理论，对功能梯度圆筒进行了受热荷载下和受内压下的弹性理论和数值分析。Kadoli[5]和Haddadpour[6]研究了特定温度边界条件下的功能梯度圆柱壳热屈曲和自由振动特性，给出了不同结构边界条件下，温度改变对壳体最小自振频率的影响。叶曦[7]基于经典壳体理论，推导了温度场作用下功能梯度材料圆柱壳自由振动方程，研究了沿厚度方向不同温度分布对功能梯度壳体频散特性的影响。Wu[8]等采用 Donnell壳理论，对热弹性圆柱壳的稳定性进行了研究。周军帅[9]将哈密顿体系引入到圆柱壳的热屈曲和热-机械载荷耦合的动态屈曲中，研究圆柱壳在热-机械载荷耦合作用下的动态屈曲特性，分析讨论了影响圆柱壳动态屈曲的主要因素。Wang等[10]用辛方法分析了等温条件下FGM输流管道的稳定性问题。综合上述文献，在输流管道横向振动问题中，采用辛方法分析温度影响下FGM输流管道的动力特性还比较少见。

本文基于Hamilton原理，引入无量纲量，推导了温度变化影响下的两端固支约束FGM输流管道的运动微分方程。通过引入对偶变量建立对偶体系，在辛空间中描述正则方程和对应的边界条件，将问题转化为哈密顿体系下的热本征值和本征解的问题。通过数值计算，讨论了管道的一阶、二阶临界流速以及在不超过临界流速的前提下温度轴力和流速对FGM输流管道无量纲复频率和挠度响应的影响。

1 运动微分方程

两端固支的FGM输流管道及其坐标系oxyz如图1所示，轴线方向为x轴，横向方向为z轴，与xz平面垂直的方向为y轴。假定管道长度为L，平均半径为R(中环线处的半径)，厚度为e，挠度为w0x,t，x方向位移为ux，输流管道内部流体速度为v0，液体的单位长度质量为ρf。将输流管道系统置于温度变化为ΔT的均匀温度场中。

图1 两端固支的FGM输流管道Fig.1 FGM pipe conveying fluid with both ends clamped

FGM输流管道材料由陶瓷和金属两种组分材料复合而成，材料成分由管道内表面的纯陶瓷(径向坐标n=-e/2)沿管道厚度方向按照幂率规律变化到管道外表面的纯金属(n=e/2)。材料属性Q(泛指弹性模量E、热膨胀系数α、热传导系数K以及管道质量密度ρ)与径向坐标n满足关系式[6]：

(1)

式中,下标c、m、eff分别表示陶瓷、金属材料以及中间的过渡材料；k∈[0,)为体积分数指数，k=0时为纯陶瓷材料，k→为纯金属材料。

材料的本构方程为：

(2)

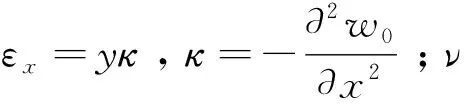
管道弯矩值和轴力值的表达式为：

(3)

(4)

式中，A为管道截面面积；

输流管道的应变能密度为：

(5)

其中，温度轴力值为：

(6)

输流管道的应变能为：

(7)

输流管道的动能表达式为：

(8)

式中，

变质量系统的Hamilton原理[11]为：

(9)

式中，t1和t2分别为任意时间段的始末时刻。

将式(7)、(8)代入式(9)，得到热环境下的FGM输流管道的运动微分方程：

(10)

引入无量纲量:

代入式(10)，得到无量纲量表示的运动微分方程：

(11)

2 辛方法求解

两端固支FGM输流管道的边界条件为：

(12)

(13)

(14)

式中，r1=4.730,r2=7.853。

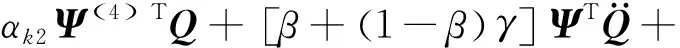
(15)

式(15)两边左乘Ψ并从0到1积分，得：

(16)

式中:

拉格朗日函数为：

(17)

引入对偶变量：

(18)

哈密顿密度函数为：

(19)

通过哈密顿正则变换，哈密顿正则方程为：

(20)

令Vτ=q1q2p1p2T，哈密顿正则方程为：

(21)

其中:

(22)

式中，

易验证H为哈密顿矩阵。

用分离变量法寻求式(21)的解，设

Vτ=ξτΦ

(23)

其中，Φ是4维向量，ξτ是τ的函数，与Φ任意分量无关。

将式(23)代入式(21)，可得

(24)

即

(25)

式中，ω为常量；i=1,2,3,4；φi为向量Φ的第i行的元素。由式(25)得：

ξτ=eωτ

(26)

HΦ=ωΦ

(27)

要使Φ向量有非零解，则式(27)的系数行列式H-ωI=0，则特征方程为：

ω4+4a2+λ12+λ22ω2+λ12λ22=0

(28)

辛本征值ω为：

ω1=

(29)

ω2=

(30)

ω3=

(31)

ω4=

(32)

求本征值对应的本征向量，设φ4=1，则本征值ωjj=1,2,3,4相对应的本征向量Φωj的各元素为：

(33)

不同本征值对应的全状态向量为：

(34)

3 计算结果分析

通过算例来分析功能梯度材料的体积分数和无量纲温度轴力对输流管道复频率、临界流速和挠度响应的影响。算例中的管道以不锈钢(SUS304)-氮化硅为材料，内表面为陶瓷，外表面为金属。并采用以下几何和物理参数：泊松比ν=0.3，内外材料密度比n1=0.29，管道壁厚e与平均半径R之比n2=0.16，弹性模量比n3=1.733，热膨胀系数比n4=0.174。

3.1 等温下均质材料输流管道的无量纲复频率

图2为材料体积分数k=0，质量比β=0.245，管道无量纲温度轴力值NT=0时，两端固支FGM输流管道第一、二阶无量纲复频率ω的虚部、实部与无量纲流速的关系曲线。

图2 固支管道无量纲复频率与无量纲流速的变化曲线Fig.2 The dimensionless complex frequencies of the clamped pipe versus the dimensionless fluid velocity

从图2(a)的纵坐标可以看出，当流速为零时，输流管道的一阶无量纲固有频率为22.37，二阶无量纲固有频率为61.67，这与文献[10]中所得结果非常接近。图2(b)中当无量纲流速为零时，ω为虚数，随着流速的增加，无量纲复频率虚部减少，实部保持为零，当流速增加到6.39时，即第一阶无量纲临界速度Ucd1=6.39时，管道运动开始处于发散失稳状态。随着流速进一步增大，第一阶模态复频率虚部一直为零，直到流速增加到9.09时，管道运动以第二阶模态形态发散，此时第二阶无量纲临界速度Ucf2=9.09，流速超过第二阶临界速度后，第一阶与第二阶复频率轨迹重合，管道耦合模态颤振产生。

上文中得到的一阶、二阶无量纲临界流速6.39、9.09与文献[12]中的一阶、二阶无量纲临界流速6.28、8.99非常接近。以某输水管道为例，管道长度L=8 m，平均半径R=0.05 m，单位长度水的质量ρf=6.647 6 kg，得到一阶、二阶有量纲临界流速252.56 m/s、359.28 m/s，该值符合工程实际。

3.2 温度影响下FGM输流管道无量纲复频率

图3为k=5和β=0.245时，两端固支FGM输流管道在不同无量纲温度轴力下，无量纲复频率的虚部、实部与无量纲流速的关系曲线。

从图3可看出以下几点：

1) 不同无量纲温度轴力下，在FGM输流管道无量纲复频率虚部中，随着无量纲温度轴力的增大，其第一阶和第二阶的无量纲临界流速都相应减小；

2) 在同一流速下，无量纲温度轴力越高，对应的复频率虚部越小；

3) 相同温度中，无量纲复频率虚部与无量纲流速的关系仍服从均质管道在无温度影响的环境中的变化规律。随后，两阶模态的复频率轨迹于虚轴结合在一起，并沿着虚轴远离原点，且温度越低远离越快。

图4与图5为k=5，β=0.245时，无量纲流速低于无量纲临界流速，不同流速情况下，FGM输流管道第一阶、第二阶无量纲复频率与无量纲温度轴力的关系曲线。不同温度环境中的FGM输流管道前两阶复频率虚部随着管道无量纲温度轴力的增大而减小；同时，在第一次达到临界流速之前，同一无量纲温度轴力情况下，随着流速的增加，FGM输流管道前两阶复频率虚部不断减少。

图3 不同无量纲温度轴力下固支管道无量纲复频率与无量纲流速的变化曲线Fig.3 The dimensionless complex frequencies of the clamped pipe versus the dimensionless fluid velocity under different dimensionless thermal axial forces

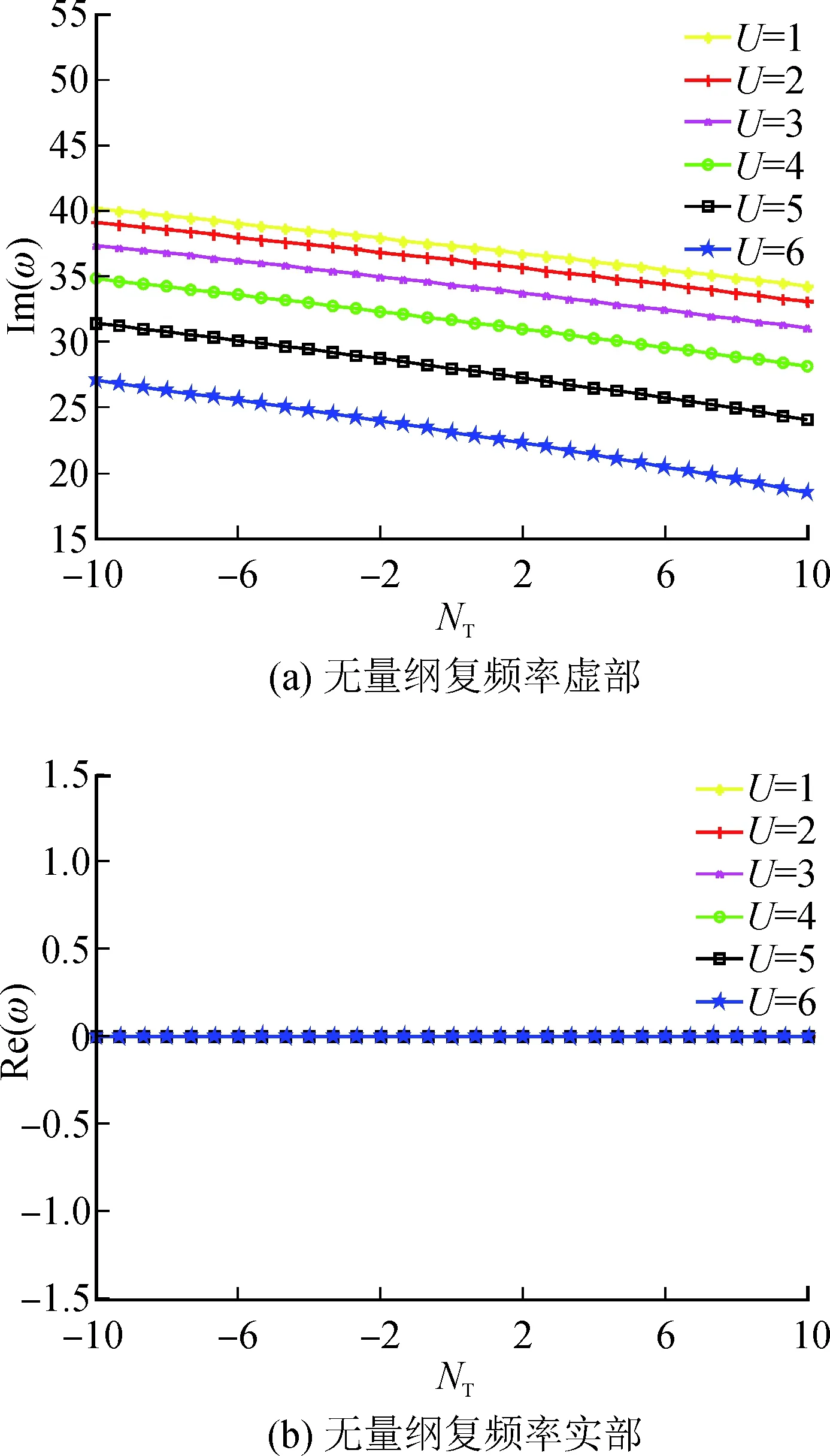
图4 固支管道第一阶复频率与无量纲温度轴力的变化曲线Fig.4 The first dimensionless complex frequencies of the clamped pipe versus the dimensionless thermal axial force

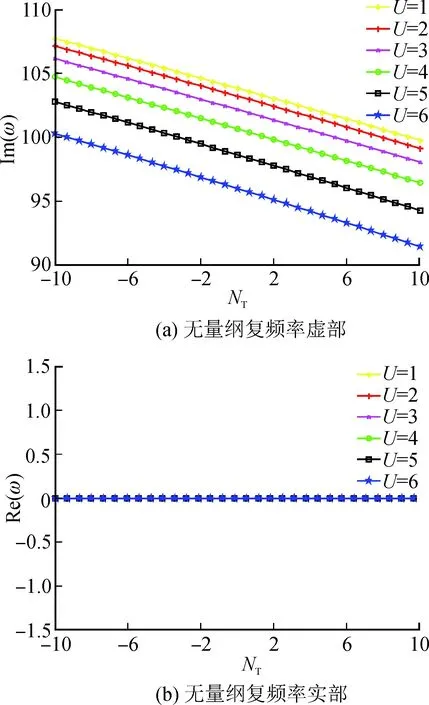
图5 固支管道第二阶复频率与无量纲温度轴力的变化曲线Fig.5 The second dimensionless complex frequencies of the clamped pipe versus the dimensionless thermal axial force

3.3 不同无量纲温度轴力下FGM输流管道的挠度响应

图6 不同无量纲温度轴力下在=0.5处固支管道无量纲挠度响应随时间的变化情况Fig.6 The dimensionless deflection response of the clamped supported pipe versus the dimensionless time under different dimensionless thermal axial forces at=0.5

图7 不同无量纲温度轴力下在=0.75处固支管道无量纲挠度响应随时间的变化情况Fig.7 The dimensionless deflection response of the clamped supported pipe versus the dimensionless time under different dimensionless thermal axial forces at =0.75

4 结 论

在温度变化的影响下，固支FGM输流管道横向振动的数值计算结果表明：

1) 在不超过第一临界速度的情况下，体积分数相同且不考虑温度的影响或同一温度时，管道固有频率随着流速的增加而减小，超过第一临界速度后，输流管道运动开始发散，超过第二临界速度后管道耦合模态颤振发生；

2) 在相同体积分数和同一流速情况下，两端固支边界条件下输流管道的固有频率随着无量纲温度轴力的增加而减小；

3) 挠度响应幅值随着无量纲温度轴力的增加而缓慢增加，挠度响应周期随着无量纲温度轴力的增加而增大。