钢桁结合梁桥约束阻尼层减振降噪方法研究

刘全民, 李小珍, 张 迅, 刘林芽

(1. 华东交通大学铁路环境振动与噪声教育部工程研究中心, 江西南昌 330013; 2. 西南交通大学土木工程学院, 四川成都 610031)

截至2017年底，我国高速铁路运营里程已超过2.5万km，同时还有大量轨道交通项目正在建设中，轨道交通带来的振动与噪声困扰日益严重。列车在钢桥和结合梁桥上运行时产生的总声压级比路基区段高5～14 dB[1]，原因之一是增加了一种声源——桥梁结构噪声。桥梁声源位置较高，辐射噪声影响范围广，且结构噪声在传播过程中不易衰减，近年来频繁遭到沿线居民的投诉，因此有必要对其进行降噪处理。从作用原理来看，在汽车、船舶、航空领域得到广泛应用的约束阻尼层(CLD)比较适合用于对钢梁的减振降噪处理。

既有研究主要通过现场试验来验证CLD对铁路桥梁的减振降噪效果[2-3]。已有的CLD结构理论分析主要集中在梁、板等简单结构，且一般只关心结构的前几阶模态损耗因子[4-5]，难以实现实际CLD桥梁车致噪声的理论分析。黏弹性阻尼材料的剪切模量是随频率变化的复模量，直接求解较困难，已有的CLD结构动力分析多将其当作不随频率变化的常数。振动与噪声响应发生在一个较宽的频率范围，黏弹性阻尼材料的弹性模量和阻尼在频域内变化较大，如果不考虑其频变特性，将导致理论计算结果出现较大的偏差。目前缺乏CLD桥梁振动与噪声的理论分析方法，对CLD用于桥梁的减振降噪机理和规律认识不足，导致将CLD用于桥梁减振降噪具有一定的盲目性，制约了铁路结合梁桥结构噪声的有效控制。

对桥梁结构进行减振降噪处理时，会限制附加CLD的质量。如果CLD的利用效率不高，也会造成材料和资金的浪费。文献[6]对桥梁腹板粘贴CLD(1.0 mm树脂层+0.3 mm金属层)后进行了现场试验，结果表明该CLD仅能降噪0～1.5 dB。由于所选的CLD厚度太小，实测的降噪效果并不明显。CLD敷设位置、几何和物理参数的选取，将明显影响其减振降噪能力，研究降噪效果随CLD参数的变化规律可以使有限材料的阻尼最大化，因此，开展用于桥梁的CLD敷设位置和结构参数的优化研究很有必要。

国内外学者就CLD敷设方式和参数对结构动力响应的影响进行了相关研究。文献[7-13]对比CLD不同参数对其用于梁、板等的减振降噪效果，而桥梁结构与梁、板明显不同，目前还少有针对CLD用于桥梁减振降噪的参数优化分析见诸报道。已有研究针对不同的研究对象对比了CLD参数对模态损耗因子或振动响应的影响，得到一些非常有价值的结果，但由于各自选择的研究对象和评价指标不同，没有形成统一的结论，有的结论甚至还是相互矛盾的。本文结合模态应变能法和统计能量分析，提出CLD桥梁的振动与噪声计算方法，为铁路桥梁的CLD减振降噪设计提供分析手段，并探讨CLD敷设位置和结构参数对高速铁路钢桁结合梁桥的车致振动与噪声的影响规律，为该类铁路桥梁的CLD减振降噪提供理论指导和应用参考。

1 理论分析方法与验证

为了计算CLD结构的振动与噪声，必须考虑千赫兹以上的高阶模态损耗因子。由于高阶模态非常密集，传统的分析方法不适用。本文拟建立新的CLD桥梁车致结构噪声的理论模型。将模态应变能分析得到的CLD子系统阻尼损耗因子代入统计能量分析功率平衡方程，同时将车-线-桥耦合振动计算的桥面板振动响应也代入统计能量方程。通过求解该方程得到桥梁各处的振动响应，最后计算桥梁在场点的结构噪声。计算流程如图1所示。

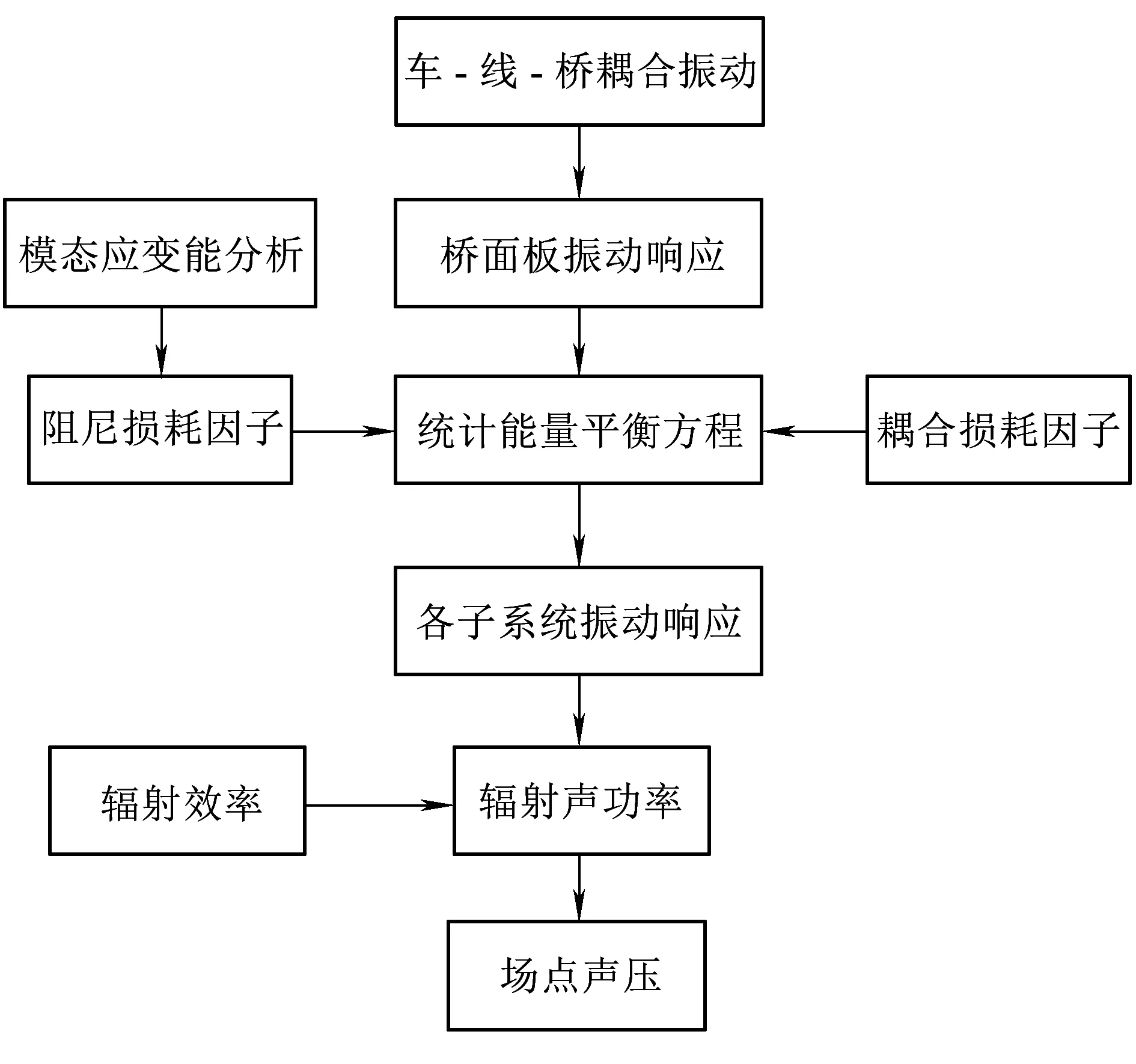
图1 计算流程

车-线-桥耦合振动计算理论参考文献[14-16]，本文不再赘述。CLD仅影响桥梁钢板的局部振动和噪声辐射，且桥梁敷设的CLD较少，对结构固有频率的改变可以忽略。假定约束阻尼桥梁的输入能量不变，仍由车-线-桥耦合振动计算统计能量分析的输入能量。

1.1 模态损耗因子计算方法

表面敷设CLD会明显提高结构的阻尼，本文根据模态应变能法计算CLD结构模态损耗因子。假定阻尼层刚度矩阵是复数，即

( 1 )

式中：KvR为阻尼层刚度矩阵实部；KvI为阻尼层刚度矩阵虚部。

ηv=KvI/KvR

( 2 )

当结构中有黏弹性阻尼材料时，结构刚度矩阵K*为复数矩阵。

K*=Ke+KvR+iKvI

( 3 )

式中：Ke为弹性层刚度矩阵。

CLD结构自由振动运动方程为

(4)

假设式(4)第j阶响应解的形式为

(5)

(K*-ω*2M)Φ*=0

(6)

假设第j阶复特征值为

(7)

式中：ηj为第j阶模态损耗因子。直接求解式(6)为复特征值问题，其计算效率较低，不利于大型模型求解。

(8)

将式(8)中的复特征向量Φj由实特征向量ΦjR代替，可得复特征值的近似值

(9)

将式(7)和式(9)的实部与虚部分别比较可得

(10)

将CLD结构由模态应变能法得到的模态损耗因子变换为1/3倍频程的阻尼损耗因子，代入统计能量方程求解可得桥梁的振动和结构噪声。

1.2 基于统计能量分析的结构噪声预测模型

对于每个子结构均为薄板的大型结构，结构之间通过铆、焊、栓的方式连接，在低频时也有大量的模态数，符合统计能量分析假设。将桥梁划分成n个子系统，可建立如下的功率平衡方程[18]

ωηE=P

(11)

式中：

(12)

(13)

(14)

其中：ω为圆频率；ηk为阻尼损耗因子；ηki为从子系统k到i的耦合损耗因子；Ek为子系统k的振动能量；Pk为子系统k的外部输入功率。

(15)

式中：ρ0为空气密度，取1.21kg/m3；c为声音在空气中的传播速度，取343m/s；σi、Si分别为板i的辐射效率和表面积。利用叠加原理计算全桥的声功率。

1.3 CLD结构噪声理论方法验证

为验证本文提出的CLD结构噪声理论分析方法，在半消声室内开展CLD工字形钢梁噪声测试试验。工字梁长2.5m，高0.5m，翼缘宽0.225m。CLD由2mm阻尼层+3mm约束层组成。表1列出了本文选用的黏弹性阻尼材料在25℃时的物理参数[19]。钢梁两端悬挂支撑，在上翼缘中心采用力锤进行激振。噪声测点S位于工字梁跨中断面，与工字梁水平距离1.5m，高度与工字梁中心一致。

表1 25 ℃时本文阻尼材料特性

理论计算首先由模态应变能法得到各板的模态损耗因子，在频带内平均转化为1/3倍频程阻尼损耗因子，将阻尼损耗因子与外部输入功率代入统计能量模型，求解可得CLD工字梁产生的噪声。图2为CLD工字梁模态损耗因子计算模型，蓝色部分为结构层，黄色部分为粘贴的CLD。

图2 CLD工字梁计算模型

CLD工字梁在力锤激励下的输入功率为

(16)

式中：Y为工字梁导纳；F为激励力。

对场点S的声压级进行对比。实测CLD工字梁在场点S的声压级为55.6 dB(A)，理论计算结果为56.8 dB(A)。从图3可以看出，两者的声压级频谱也大致相同，说明本文的CLD结构噪声计算方法是可靠的。

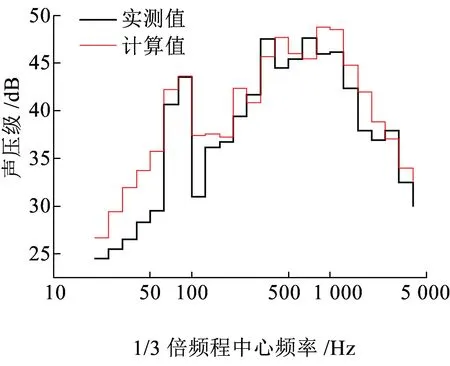
图3 实测与计算声压级

2 CLD敷设位置

2.1 桥梁概况

简支钢桁结合梁桥在石太、合宁、遂渝等多条线路使用较广泛，因此本文以某有砟64 m双线简支钢桁结合梁桥为研究背景。该桥设计行车速度250 km/h，线间距4.6 m。主桁为Warren桁架，高12.3 m，中心距11 m。桥面系采用钢纵横梁加混凝土桥面板的结构形式，纵梁4片，横梁布置在下弦节点及节间中部。端横梁截面为箱形，其他纵、横梁截面均为工字形。通过纵梁及主桁下弦上翼缘的栓钉实现组合结构的连接。线路中心处桥面板厚度为23 cm，栓钉连接处桥面板厚度为28～34.6 cm。图4为该桥主桁立面和桥面系平面图。

图4 试验桥梁结构示意(单位：mm)

2.2 桥梁结构噪声

在车-线-桥耦合振动计算中，桥面板采用板单元，桥梁其余构件采用梁单元。理论计算中列车采用CRH3型动车组，编组构成为4动4拖，计算车速250 km/h。轨道不平顺在3～80 m波长范围采用德国低干扰谱[20]。由于短波不平顺对桥梁辐射结构噪声有重要影响[21]，因此在高低不平顺中再叠加文献[22]推荐的波长为0.016～3 m的粗糙度谱。当车速为250 km/h时，激励频率可达到4 340 Hz。计算时，时间积分步长取0.000 1 s。

本文确定的噪声考察点M位于桥梁跨中断面，与线路水平距离25 m，竖向高于轨面3.5 m。由于该桥构件较多，将其按纵梁、横梁、近主桁、远主桁、桥面板、上平纵联分为6部分，计算各部分在场点M处的声压级，列入表2。从表2可以看出，对声压级的贡献从大到小依次是近主桁、纵梁、远主桁、横梁、桥面板、上平纵联。计算结果还表明，该桥在场点M处的A声级较大，高于70 dB(A)，故有必要对高速铁路上的此类桥梁进行降噪处理。

表2 桥梁各部分声贡献量 dB(A)

2.3 CLD敷设杆件

桥面板振动先引起纵横梁振动，纵横梁通过下弦将振动能量传递至整个主桁，故本文选取声贡献量最大的4个部分，在纵、横梁和主桁上安装CLD。

组成钢桁梁的板件较多，采用本文提出的理论计算方法分析纵、横梁和主桁的每一块板件在场点M处产生的结构噪声，选取声贡献大的板件粘贴CLD。纵梁各板在场点M处产生的噪声为39.2～50.1 dB(A)，横梁各板在场点M处产生的噪声为35.1～44.7 dB(A)，近主桁各板在场点M处产生的噪声为38.2～51.3 dB(A)。根据噪声控制原理，对最高声压级向下5 dB(A)范围内的板进行噪声控制，最终确定在全部纵梁、主桁下弦及中部7根横梁的腹板粘贴CLD。

3 CLD结构参数优化

采用本文提出的理论分析方法探讨桥梁结构噪声降低量随CLD结构参数的变化规律。首先，通过对比单块板件敷设不同面积比的CLD时场点M处的降噪量来确定CLD在单块板上的敷设面积比。经调研初步选用的CLD参数见表3。

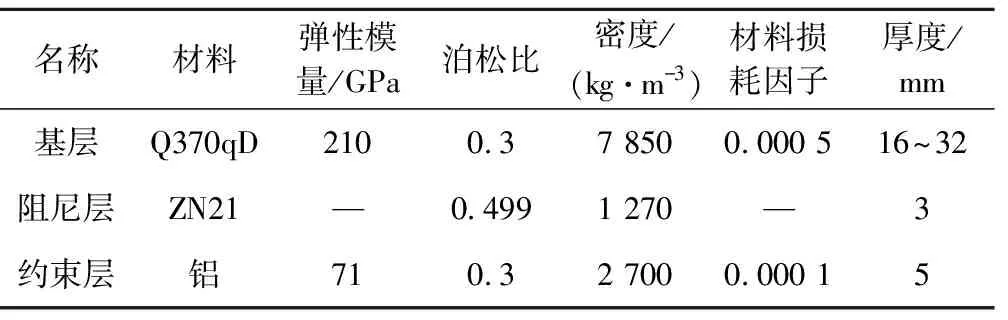
表3 初始参数

计算结果表明，在纵、横梁腹板上分别粘贴30%的CLD可使其在场点M产生的结构噪声减小8.5 dB(A)、11.3 dB(A)，在下弦腹板布置50%的CLD可使其在场点M的结构噪声减小3.7 dB(A)。可见，单块构件的降噪效果已经较明显，所以确定CLD在纵、横梁腹板粘贴面积比为30%，在下弦腹板粘贴面积比为50%。

在设计CLD控制振动与噪声时，应选用阻尼大、密度小的CLD。本文针对纵梁腹板，探讨阻尼层、约束层模量和阻尼层、约束层厚度对CLD降噪能力的影响规律。

3.1 阻尼层剪切模量

设表1中的阻尼材料剪切模量为1.0G，当阻尼材料剪切模量各自取0.1G、0.5G、1.0G和10G时CLD的降噪效果对比如图5所示。由图5可见，阻尼层剪切模量对其降噪效果影响明显，阻尼层剪切模量增大对高频降噪有利，对中低频段噪声的控制并不是简单的正反比关系；安装CLD使结构噪声峰值频率略向低频变化。计算结果表明分析工况中，阻尼层剪切模量为1.0G时的CLD对纵梁腹板的降噪效果最佳，达到8.5 dB(A)。

图5 阻尼层不同剪切模量下的声压级

3.2 约束层材料

纵梁腹板分别粘贴铝、钢CLD时噪声对比如图6所示。在其他参数相同的条件下，与铝约束层CLD相比，钢约束层CLD在全频段内的降噪能力更强，对中低频段的结构噪声降噪效果更明显。虽然与钢约束层相比，铝约束层CLD对纵梁腹板降噪量少1.3 dB(A)，但已经能达到8.5 dB(A)的降噪效果。铝材具有密度小、不易生锈、易于加工成型等钢材不具备的优点，因此下文分析中仍采用铝约束层。

图6 铝、钢约束层工况下的声压级

3.3 阻尼层厚度

纵梁腹板表面单侧粘贴30%的CLD，铝约束层厚度设为5 mm，阻尼层厚度分别取1、2、3、5 mm共4种工况进行分析。由图7可知，4种工况的CLD均能明显减小纵梁腹板在场点M产生的噪声，即降噪量对1～5 mm范围内的阻尼层厚度参数不敏感。阻尼层厚度增加不利于高频降噪，但对低频降噪有利。从计算结果来看，2 mm厚的CLD阻尼层对纵梁腹板的降噪效果比1、3、5 mm工况稍好。

图7 不同阻尼层厚度下的声压级

3.4 约束层厚度

当纵梁腹板表面单侧粘贴30%的CLD时，阻尼层厚度取3 mm，铝约束层厚度分别为1、2、3、5 mm的4种CLD敷设工况与不敷设工况对比如图8所示。图8表明噪声降低值对约束层厚度较敏感。约束层越厚，整个频段内的噪声降低值均越大，在低频段降噪效果更明显。约束层厚度为5 mm时，纵梁腹板在场点M处产生的噪声减小8.5 dB(A)。

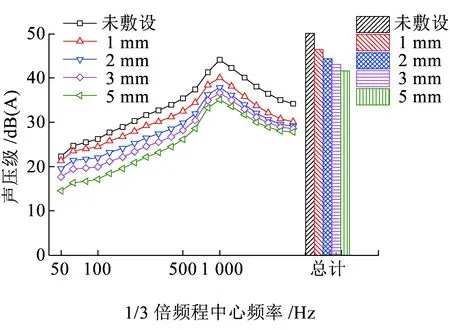
图8 不同约束层厚度下的声压级

4 CLD桥梁减振降噪评估

对该64 m钢桁结合梁桥采用以上优化参数的CLD进行减振降噪效果分析。阻尼层材料不变，厚度取2 mm；约束层采用铝质材料，厚度取5 mm。共安装CLD 254.5 m2，附加质量4.1 t，占全桥恒载的0.15%，可忽略其对桥梁恒载的影响。

该桥安装CLD前后跨中纵梁腹板振动速度频谱如图9所示。从图9可见，纵梁腹板振动速度在整个分析频率范围内都有明显降低。敷设CLD后，纵梁、横梁和下弦杆腹板的振动速度级分别降低15.6、15.5和6.2 dB，可见CLD可大幅减小钢梁的振动响应。纵梁和中横梁的腹板厚16 mm，下弦腹板厚28、32 mm，纵横梁腹板比下弦腹板薄得多，故纵横梁振动降低较下弦更明显。相同的CLD构造对厚度越小的基层，减振能力越强。

图9 纵梁腹板振动速度频谱

安装CLD前后该桥在场点M处产生噪声的频谱如图10所示。粘贴CLD使全频段结构噪声大幅减小，说明敷设CLD能够有效控制钢梁的结构噪声，且高频降噪效果优于低频。另外，敷设CLD后噪声峰值频率降低。

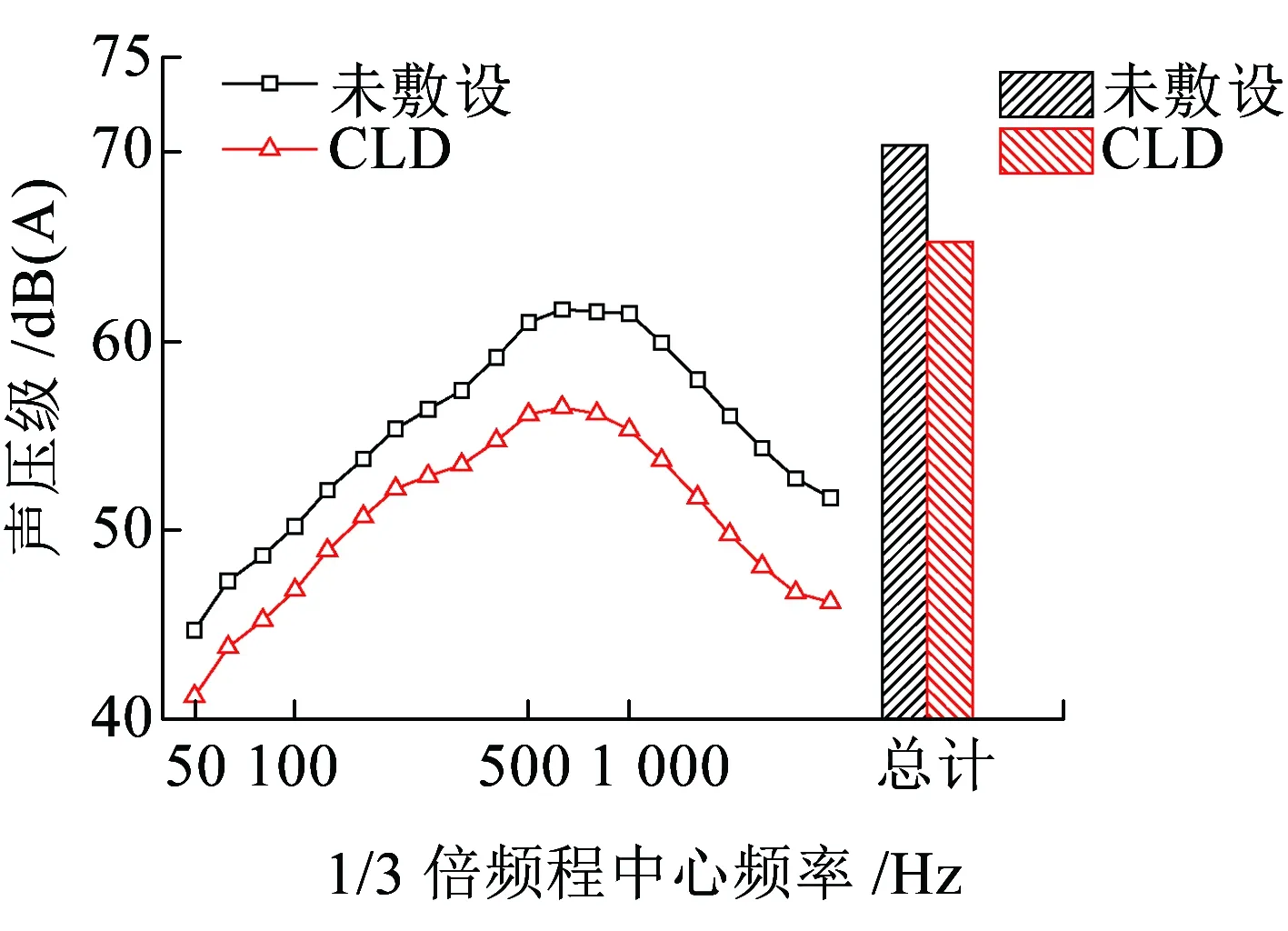
图10 场点M噪声频谱图

安装CLD前后桥梁各构件在场点M处产生的声压级见表4，该处总结构噪声减小5.1 dB(A)，其中近主桁、纵梁、远主桁、横梁、上平纵联和桥面板产生的噪声依次减小6.2、6.7、6.3、3.0、3.1、0 dB(A)。混凝土桥面板处于振动传递路径前端，钢桁梁安装CLD对其响应几乎无影响。另外，上平纵联未粘贴CLD，但其辐射噪声也有降低，是由于对振动传递路径前端的构件安装CLD消耗振动能量，传递到路径后端构件的振动减小，因此声辐射也减小。

表4 场点M声压级 dB(A)

5 结论

本文结合模态应变能法和统计能量分析，建立CLD桥梁车致振动与噪声的理论计算模型，模型中采用更精确的频变阻尼材料特性，通过CLD工字梁噪声试验验证了该模型的正确性，最后分析了桥梁结构噪声降低值随CLD参数的变化规律。结论如下：

(1)阻尼层剪切模量增大对高频降噪有利，对中低频段噪声的控制并不是简单的正反比关系。与铝约束层CLD相比，钢约束层CLD在全频段内的降噪能力更强。

(2)CLD的噪声降低值对1～5 mm范围内的阻尼层厚度参数不敏感，对约束层厚度较敏感。约束层厚度增加，整个频段内的噪声降低值均增大，且在低频段降噪效果更明显。

(3)本文在全部纵梁、主桁下弦及中部7根横梁的腹板安装CLD。纵、横梁腹板CLD安装面积比为30%，下弦腹板CLD安装面积比为50%。共安装CLD254.5 m2，附加质量4.1 t，占全桥恒载0.15%。安装CLD后，该桥纵梁、横梁和下弦杆腹板的振动速度级分别降低15.6、15.5和6.2 dB；安装CLD使全频段结构噪声大幅减小，场点M处声压级降低5.1 dB(A)，具有较好的减振降噪效果。