基于参数化轨迹的TAEM段在线制导方法

樊朋飞，刘蛟龙，凡永华，闫杰

1. 西北工业大学 航天学院，西安 710072 2. 北京航天自动控制研究所，北京 100854

末端区域能量管理(TAEM)段连接再入段与着陆段，将可重复使用运载器(RLV)从再入段后的高能量状态消耗至安全着陆所需的低能量水平，同时通过地面轨迹的控制将RLV导引至跑道前方合适的位置并将航向角对准跑道方向，是实现无动力水平着陆的关键环节[1-3]。基于预先规划飞行剖面的TAEM段制导技术成熟可靠，在航天飞机数十年的使用中得到了验证[4]，但对于较大初始状态散布、气动偏差和执行机构故障等极端条件适应能力较差，并且不适用于没有阻力控制装置的无动力飞行器(等同于航天飞机减速板故障)[5]。

基于未来RLV对安全性、可靠性和低运营费用的更高要求，研究具备自主决策、在线轨迹生成/轨迹重构、自适应制导与容错控制等功能的先进制导控制技术(AG&C)成为新的趋势[6-10]。针对TAEM段在线轨迹生成和制导问题，Kluever[11]研究了一种快速轨迹生成算法，通过在线生成的动压剖面和迭代两个地面轨迹几何学参数迅速生成符合约束条件的参考轨迹。Hull等[12]将TAEM段和进场着陆段视为整体，通过6个关键参数对参考轨迹进行完全描述，闭环积分运动方程获得着陆点状态偏差，连续更新轨迹参数逐渐使参考轨迹满足着陆约束条件。Horneman[13]研究了适于低能量再入飞行器的TAEM段改进制导方法。王宏伦等[14-15]分别采用轨迹优化和剖面规划的方法研究了无动力飞行器应急着陆的轨迹生成问题。Lan等[16]设计了在线可调的动压剖面以增加设计的自由度，在轨迹重塑中能同时更新纵向和侧向参数，使RLV具有更强的航程控制能力。现阶段，以数值积分为核心的TAEM在线制导技术在应用中仍面临一些困难。首先，反复积分运动方程需占用较多弹上计算资源，效率低下且对硬件要求高；其次，积分运动方程依赖对气动、环境参数的精确在线辨识，这在技术上仍具有较大难度。

在提高TAEM段在线制导效率、保证实时性方面，较普遍的方法是消去运动方程中的时间变量以降低方程的维度，以高度或能量为自变量、采用大积分步长进行快速积分预测[2-3,8,11-12]的思路。在此基础上，周敏等[17]则通过在航向调整段(HAC)前增加一段可获得轨迹解析解的直线预测捕获段(PASL)的方式，在解析解可覆盖的时间段内以PASL的末状态为起始点规划高度、速度剖面。该方法避免了需要在TAEM起始阶段完成轨迹规划的问题，其缺点是只能进行一次在线规划，灵活性较差。Liang等[18]通过提高轨迹参数搜索和迭代效率的方式提高在线规划效率，采用随高度分段线性变化的航迹倾角剖面描述纵向轨迹，在飞行航程确定后，末端速度与剖面的唯一参数呈单调关系，经过2～3次迭代便可获得满足要求的参考轨迹，在台式计算机上的用时不超过1 s。Kluever和Neal[19]、Mu等[20]研究了具有明显效率优势的查表预测法在TAEM段制导中的应用问题。其中，Kluever和Neal以“准平衡滑翔”假设为基础，离线生成了随滑翔效率变化的高度-动压剖面并计算得到滑翔效率、能量高度与飞行航程的关系表，通过查表实现对飞行器航程的高精度预测，然而该方法只针对直线飞行状态，不需考虑侧向机动造成航程损失的问题，且当模型参数发生变化后，基准剖面表需要重新计算，这对于在线制导是不可接受的。Mu则离线规划了一系列由多项式构成的高度-动压剖面，沿剖面求解纵向运动方程获得各剖面的高度、轨迹倾角、攻角等变量与待飞航程的关系表。在初始阶段，根据估算的地面航程选择相应参考剖面，并对该剖面的高度、速度信息分别进行跟踪。这种方法同样没有在规划中考虑飞行器转弯造成的轨迹偏差，文中因转弯和模型偏差引起的速度误差通过飞行器的减速板消除，仿真中末端速度的较大散布则说明了方法效果的有限性。同时，由于剖面初始状态固定，该方法也无法覆盖初始能量出现偏差的情况。

动力学模型中的气动、大气等主要参数由于建模误差、控制面故障和飞行环境等因素影响，在实际飞行中具有不确定性。针对这一问题在制导算法中的研究比较少，在大多数研究[12,16,18-19]中，通常假定模型各项偏差可通过在线辨识的方式准确获得，从而作为已知量在制导算法中使用，这种假设忽略了模型在线辨识的技术难度，实际上是避开了模型不确定性问题。少量文献[17,20]则认为可通过减速板的速度控制能力抵消未知偏差的影响，这使得算法具有一定局限性，即需减速板的控制能力充足且工作状态良好，对于不含减速板的飞行器或发生故障的情况则不适用。

本文基于实用化的思路研究了可重复使用再入飞行器末端能量管理段的在线制导问题。综合考虑算法对于计算效率的需求和获取信息(模型参数)的限制，着重研究了基于高度-动压的飞行剖面生成和轨迹在侧向机动和模型偏差影响下的航程精确预测问题，以及约束条件下多轨迹参数的更新策略。首先，研究了动压包线的规划和参考剖面的生成问题。不同于只针对固定初始和末端状态规划动压剖面的方式[16,20]，本文在参考剖面的规划中考虑了初始状态不确定因素，除可飞动压的上、下边界外，增加了最大能量边界，使得动压剖面不需从固定的初始点生成，而只要求初始高度、动压不超出3条边界形成的闭合包线。动压剖面采用参数化描述，之后分别沿各剖面计算出航程与剖面参数、倾侧角和能量高度的对应关系，将其存为三维数表。侧向轨迹由大小和位置可变的校正圆柱确定，其各分段航迹信息根据当前状态计算。随后，为使待飞航程的预测更加精确，本文在预测中加入了文献[19，20]中未考虑的侧向机动和模型偏差因素。先根据已计算的地面航迹信息，采用分段查表的方式分别求取RLV两次侧向机动的额外能量损耗，以此对直线飞行状态下的航程预测值进行第1步修正；在未获得故障信息和模型各项偏差辨识结果的情况下，通过在线估计的航程修正系数对待飞航程进行二次修正。最后，研究了纵向、侧向轨迹参数更新问题。多轨迹参数在提高了轨迹调整能力的同时，带来了多轨迹参数的协调更新问题，不同于文献[16]中纵向和侧向轨迹参数更新只与航程偏差相关的处理方式，本文综合考虑了纵向参数余量和侧向转弯性能，通过增加类死区形式的更新约束和合理的更新权重设计，提高了轨迹参数的匹配性。通过数值仿真对制导算法进行了验证，结果表明：该方法对于初始散布具有较强的鲁棒性以及较高的制导精度，对于突发故障具有快速的响应能力和适应性，并且具有较高的在线制导计算效率。

1 运动学建模

将飞行区域的地面视为惯性平面，以进场着陆窗口(ALI)处的地表为坐标原点，沿跑道中线方向为X轴建立三自由度质点运动方程：

(1)

(2)

(3)

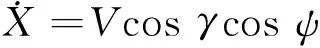
(4)

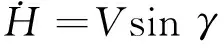
(5)

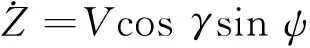
(6)

式中：状态量V、γ、ψ、X、H和Z分别为飞行器的速度、航迹倾角、航向角、纵向位置、高度和侧向位置；μ为倾侧角；m为质量；g为重力加速度常量。升力L和阻力D的表达式为

(7)

(8)

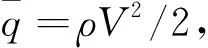
(9)

式中：零升阻力系数CD0和诱导阻力系数KCL为Ma的函数，不同马赫数下CD随CL变化的关系如图1所示，飞行器质量m=61 462 kg，参考面积Sref=220.2 m2。

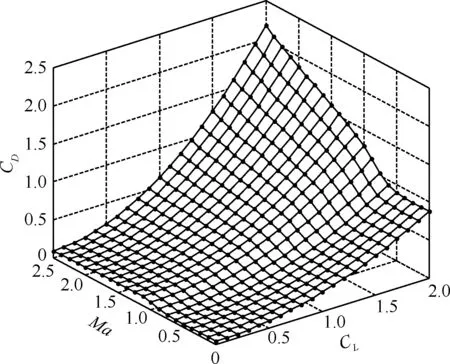
图1 阻力系数与升力系数和马赫数关系图Fig.1 Variations of drag coefficients with lift coefficients and Mach number

2 TAEM段在线制导算法

TAEM段在线制导算法的结构如图2所示，算法主要包括参考指令生成、制导律、轨迹预测和轨迹参数更新4个部分。由参考指令生成算法根据当前轨迹参数和飞行状态计算动压和航向角指令。制导律采用反步法设计，生成升力系数和倾侧角指令以实现对参考指令的精确跟踪。轨迹预测算法则根据当前能量状态和轨迹参数对轨迹信息进行估计，包括待飞航程、地面航程、校正转弯倾侧角等。参数更新算法根据当前航程偏差和相关约束条件实现对轨迹参数的修正。

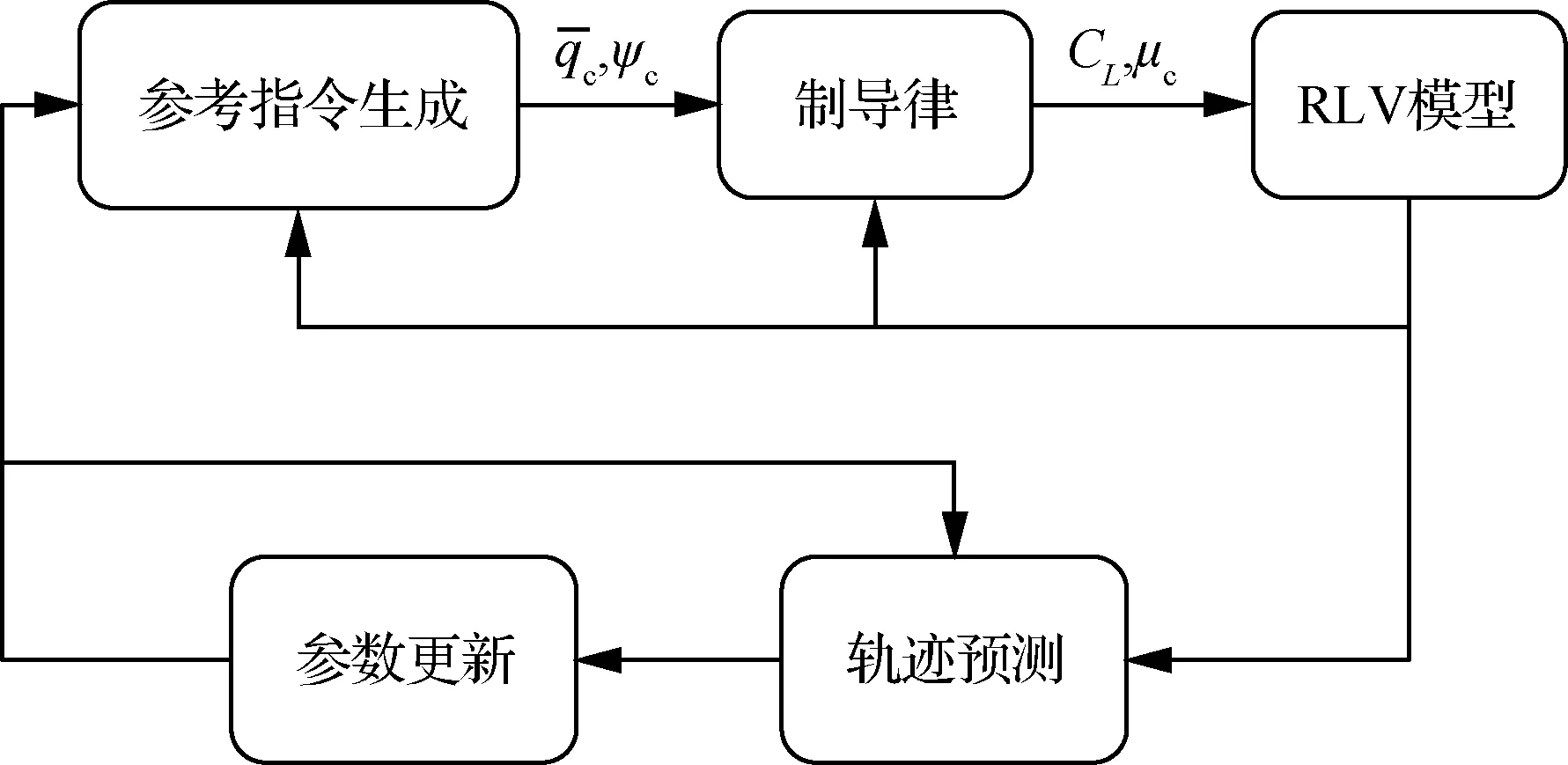
图2 TAEM段在线制导算法结构图Fig.2 Architecture of in-flight guidance algorithm in TAEM phase

2.1 纵向指令生成

将动压作为参考剖面具有诸多优点，因而在TAEM段制导技术的研究中被广泛采用[11-12,16,21]。本文的参考动压剖面在动压包线内生成。动压包线主要由最大动压约束和最大升阻比滑翔动压确定。实际飞行中要求尽快减速以便进行航向校正转弯，因此并不希望动压长时间停留在较高值，且尽可能使飞行器以平衡滑翔状态飞至着陆窗口，即末端的动压变化率不宜过大。综合TAEM末端约束条件，给出动压边界的描述如图3所示。

完整动压包线包括动压上下边界和最大能量高度边界，动压上下边界和参考剖面可统一用式(10)描述：

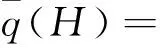
(10)

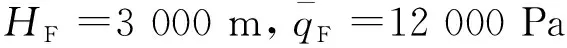
(11)

它表示飞行器单位重量具有的动能和势能总和，这里设定飞行器初始点最大能量高度不超过47 763 m。由式(11)可知初始高度确定后，上下边界的初始动压按式(12)计算：

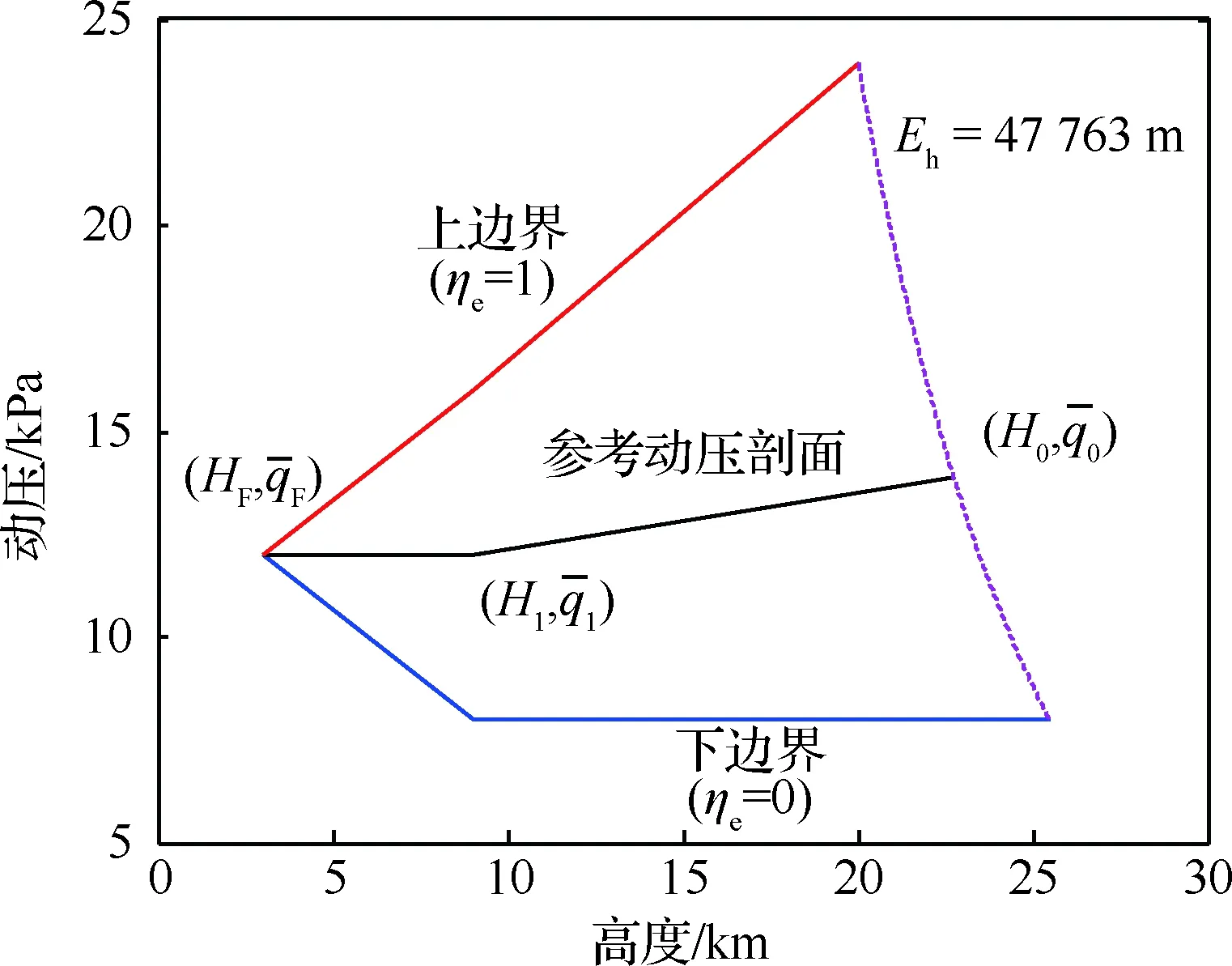
图3 动压边界与高度-动压剖面图Fig.3 Profile of dynamic pressure boundary and height-dynamic pressure

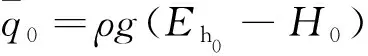
(12)

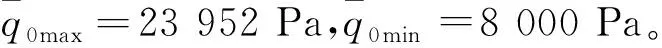
(13)

H0=H0maxηe+H0min(1-ηe)

(14)

则当ηe从0变化至1时，动压剖面由下界过渡至上界，图3中的黑色曲线为ηe=0.5时的动压剖面。将Eh对时间求导，可得

(15)

可知，当以较大动压剖面飞行时，相同高度下阻力和速度更大，能量消耗快。ηe不仅表示了参考动压剖面在动压包线内的位置，也代表了沿该条参考剖面飞行时的能量消耗速率，因此将其称作能量因子。

(16)

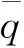
(17)

(18)

注意这里由于β随H变化极小，故忽略了两者之间的导数项。式(17)给出了跟踪参考动压剖面时D与γ之间的关系。

又有离散状态下：

(19)

定义ηm=cosμ，利用上述方法依次计算不同ηe、ηm时的Eh-R关系，将其存为三维数表，其结果如图4和图5所示。这样，已知当前能量高度Eh、ηe和ηm，便可由数表插值获得由当前状态

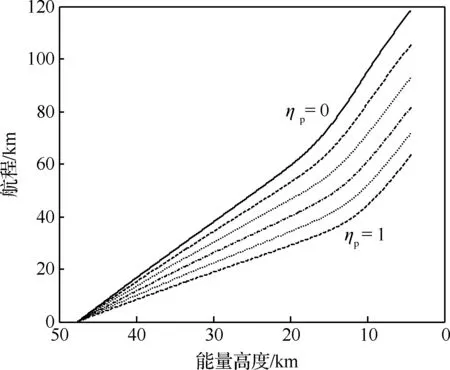
图4 ηm=1时航程随能量因子和 能量高度的变化曲线Fig.4 Variation of range with energy factor and energy height at ηm=1

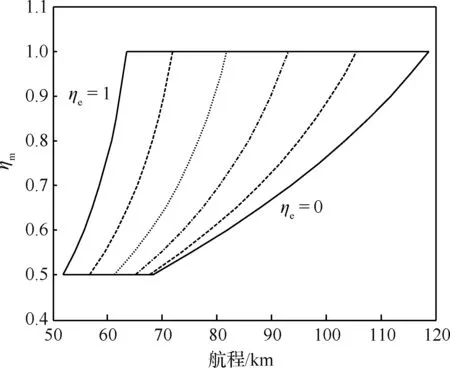
图5 航程随能量因子和ηm变化曲线Fig.5 Variations of range with energy factor and ηm

至目标能量高度Etar时的待飞航程：

Rtogo=R(ηm,ηe,Etar)-R(ηm,ηe,Eh)

(20)

2.2 地面航程计算与航迹指令生成

TAEM段的地面航迹如图6所示，根据飞行阶段不同，地面航迹分为3段：捕获段、航向校准段和进场前飞行段。描述地面航迹的参数为校正圆的位置xHAC和半径最终值RF以及校准转弯模式。已知上述参数情况下，可计算从当前位置到ALI的地面航程。地面航迹一般由两个曲线段和两个直线段组成：

sTAEM=sAT+sStr+sHAC+sPF

(21)

式中：sAT和sStr分别为捕获段转弯长度和转弯结

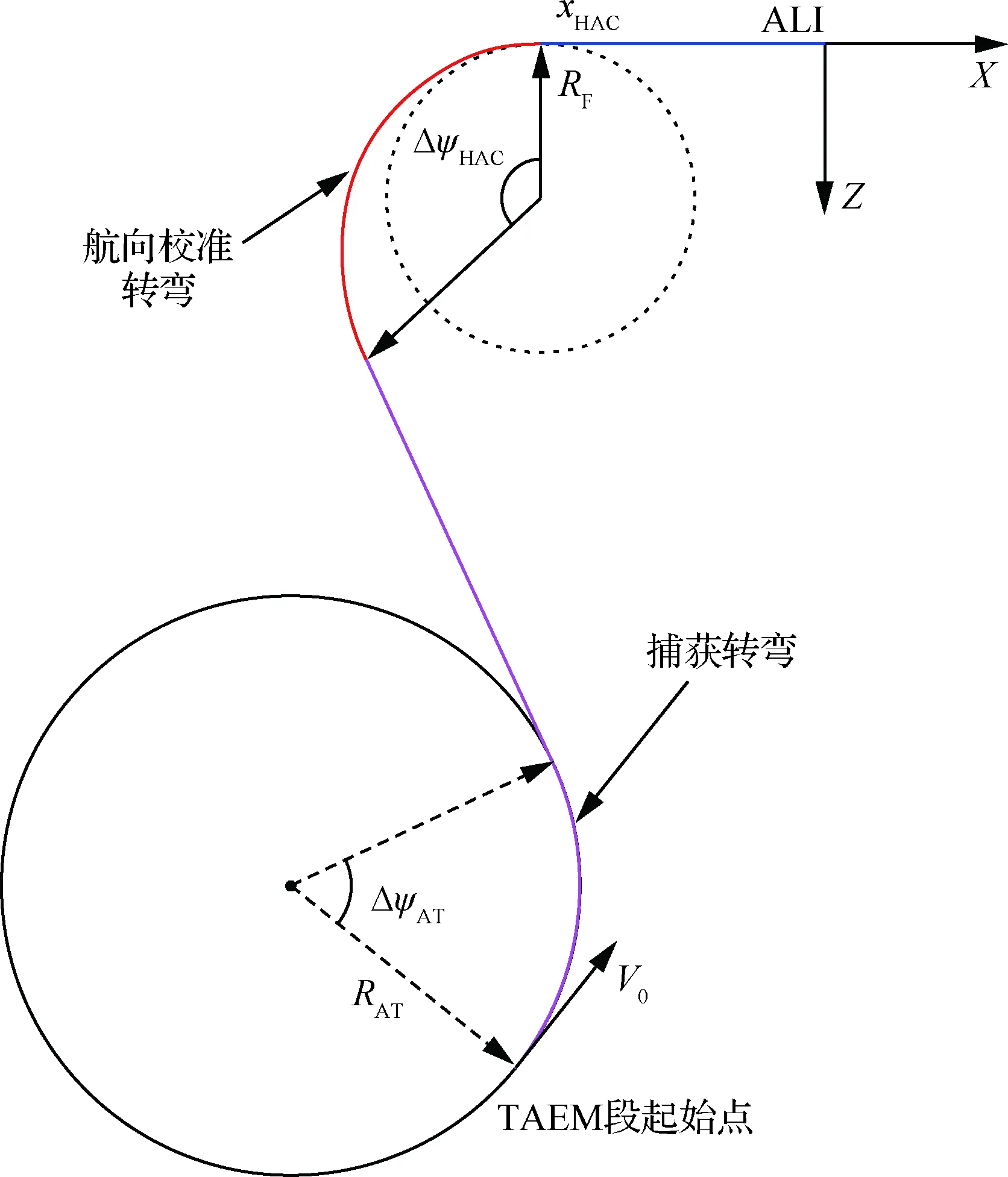
图6 TAEM地面航迹Fig.6 Ground track of TAEM

束后的直线段长度；sHAC、sPF为航向校正转弯和进场前飞行段的长度。

捕获段转弯(Acquisition Turn)的时间通常较短，可将其视为一段圆弧，圆弧的长度为

sAT=RAT|ΔψAT|

(22)

式中：RAT为圆弧的半径；ΔψAT为当前速度矢量与航向校正圆柱切点的方向偏差。RAT可用式(23)近似计算：

(23)

式中：μAT为捕获段转弯的倾侧角估值，这里取其约束值μAT=50° 。

航向校准转弯(HAC Turn)的转弯半径为转弯角度ΔψHAC的二次函数：

(24)

这样，随着剩余转弯角度的减小，HAC转弯的半径逐渐缩小至最终值RF，R2为常值系数，取R2=300 m/rad2。将式(24)对ΔψHAC求积分，可得航向校准段的长度：

(25)

sPF的长度通过校正圆的位置参数xHAC计算。对于ΔψAT、ΔψHAC以及sStr的求取方法详见文献[4，20]。

计算出上述参数后，各飞行阶段的航向角指令ψc便可给出。在捕获段，飞行器需要将航向对准校正圆柱的切点，此时指令为

ψc1=ψ+ΔψAT

(26)

进入航向校准段之后，飞行器的跟踪轨迹为与X轴相切的螺旋线。如图7所示，飞行器瞬时水平速度Vh，航向角为ψ，与校正圆柱圆心距离r，则其与螺旋线切点的距离为

Δr=RHAC-r

(27)

ra为螺旋线切点处的方向矢量，与X轴夹角为ψa，可由螺旋线切点处的斜率计算出，则Vh与ra的夹角为ψa-ψ，则Δr的变化率为

(28)

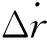
(29)

进场前飞行段采用侧向位置控制：

ψc3=-KzZ

(30)

2.3 轨迹预测算法

飞行中需要预测的轨迹信息包括待飞航程Rtogo和航向校准转弯开始时的需用倾侧角μHAC0。μHAC0作为待约束量，用于避免转弯时倾侧角需用量超出限制。待飞航程的初步估计可根据式(20)计算，能量因子ηe确定时，可先假定飞行器沿直线飞行，即ηm=1，则待飞航程为

(31)

式中：Eend为能量高度的末端值。然而实际飞行中由于飞行器转弯(捕获转弯、航向校准转弯)和模型偏差等因素影响，飞行器的实际飞行距离与该估计值存在较大偏差，因此需对其进行修正。

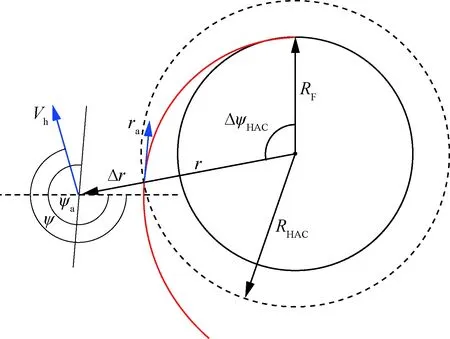
图7 航向校准转弯轨迹跟踪Fig.7 Ground track of HAC turn

2.3.1 侧向机动航程损失估计

侧向机动的航程损失是由机动时额外的能量消耗造成的。为简化叙述，仅以捕获转弯为例进行分析和计算，航向校准转弯的航程损失计算方法与之类似。

eAT=s2-s1-sAT

(32)

同理，可计算得到航向校准转弯开始时的能量高度Eh3。由于航向校准转弯阶段的倾侧角通常不是常值，这里取其平均值：

(33)

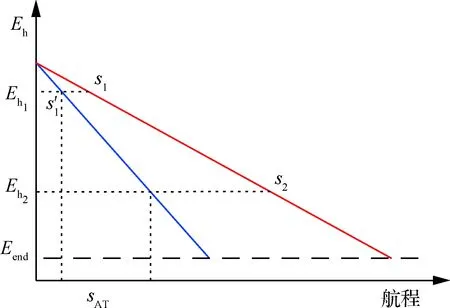
图8 捕获转弯的航程损失Fig.8 Range loss in acquisition turn

(34)

2.3.2 模型偏差航程误差估计

模型偏差主要包括气动参数和大气密度偏差。在偏差情况下，飞行器跟踪相同参考动压剖面时的航程会发生变化，通过在线估计气动参数和大气密度的偏差，并计算出偏差条件下的准确航程是十分困难的。积分式(16)可得

(35)

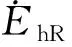
对式(17)进一步整理可得

(36)

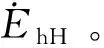
(37)

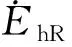
(38)

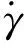
(39)

联立式(37)～式(39)有如下关系：

(40)

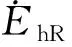
(41)

最终的航程预测值Rtogo为

(42)

需要说明的是，轨迹预测所需动压值均由当前高度下的标准大气计算，不依赖实际大气信息，而升力、阻力信息则通过惯性器件测量获得，避免了模型偏差的直接估计问题。

2.4 轨迹参数更新算法

轨迹参数更新的目的在于消除待飞航程和地面航程之间的偏差，同时要求轨迹满足一定的约束，即航向校准转弯时的倾侧角不超过60°。飞行轨迹的参数包括纵向参数ηe，地面轨迹参数xHAC、RF以及航向校准转弯模式。其中航向校准转弯模式需在TAEM开始时进行确定，轨迹参数则在每个制导周期内更新。

轨迹参数的更新可分为2个阶段：第1阶段为TAEM开始至航向校准转弯之前，此阶段上述3个轨迹参数均可进行更新，需对每个参数的更新权重进行分配；第2阶段为校准转弯开始之后至TAEM段结束，此时可调整参数仅为ηe。为减少第1阶段的参数更新数目，考虑到xHAC和RF存在对应关系，即圆柱离ALI较远时RF的取值也应较大以生成更远的地面航程或适应较大的转弯速度，令xHAC与RF满足如下关系：

(43)

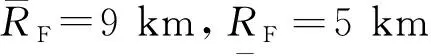
(44)

给出第k+1制导周期的轨迹参数更新方程为

(45)

式中：

K为系数矩阵；Δdk为偏差向量。偏差项Δs=sTAEM-Rtogo为地面航程与待飞航程之差，

(46)

为校正转弯倾侧角余弦值与约束值的偏差。

可以看出，除航程偏差Δs外，其他偏差项均只在超出约束限制时对轨迹参数更新起约束作用。一般地，飞行器纵向位置位于校正圆柱中心右侧时，增加飞行距离有利于减小倾侧角，K13取正号，位于左侧时则情况相反。需要说明，更新方程中的约束关系并非硬约束，且不同约束可能出现竞争关系，尽管如此，通过合理选择更新矩阵中的权重系数，能够满足绝大多数情况的要求。根据经验，矩阵K中系数取K11=0.004，K12=-160，|K13|=200，K21为Eh的线性函数，其值由最大能量高度时的-0.2×10-8递减至末端能量高度的-0.1×10-6。

2.5 轨迹跟踪制导律

考虑到动压变量的强非线性特征，本文采用具有反步法结构的动态逆控制方法[12]对制导指令进行跟踪。这里做适当改进，且略去设计过程，仅给出控制指令的计算公式。

1) 动压控制

首先由动压偏差得到航迹倾角指令：

(47)

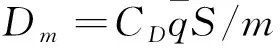
(48)

考虑过载指令的响应，得到升力系数输入：

(49)

式中：Kqp=0.3，Kqi=0.03，Kγ=1.5，Kny=6，过载指令限幅Nylim=[0.5，2.5]。

2) 航向角控制

倾侧角指令根据航向偏差计算：

(50)

同样考虑倾侧角指令的响应过程

(51)

式中：Kψ=0.5，Kμ=6。倾侧角指令限幅：捕获段±50°，航向校准段±60°。

3 仿真分析

为了验证本文TAEM在线制导算法的有效性，基于MATLAB的SIMULINK仿真环境构建了数字仿真模型，编写实现了上述算法，仿真采用定步长ODE4龙格-库塔法，仿真步长5 ms，轨迹参数的更新周期为20 ms，仿真结束条件为H≤3 km。仿真分为3个部分，分别验证本文算法对3类因素的适应能力：① 初始位置和航向散布；② 初始能量状态散布；③ 突发故障。其中，3.3节的后半部分则对算法的计算效率进行了分析对比。

3.1 初始位置、航向散布

仿真取初始条件H0=22 736 m、V0=700.4 m/s、γ0=-6.6°，该状态对应能量高度Eh0=47 763，ηe0=0.5。初始位置、航向条件取表1所示5组数据。可以看出轨迹1～4的起始点位于航向校正圆柱可取最近值(-10 000 m)的右侧，距离ALI的直线距离依次递减，航向角依次增大，曲线5则位于校正圆柱左侧。

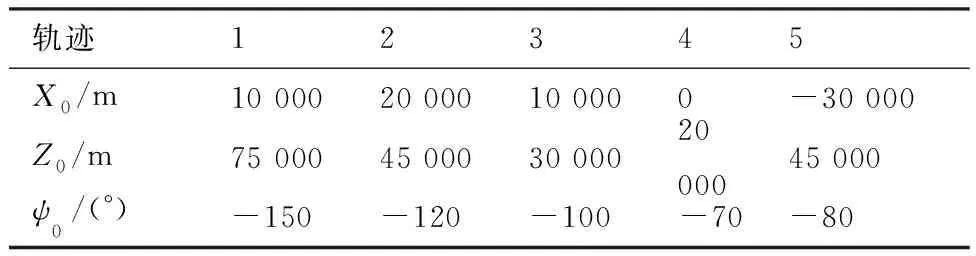
表1 初始位置、航向条件Table 1 Initial position and heading angle

图9为地面航迹，图10分别为动压、能量因子和航迹倾角曲线，表2为地面轨迹最终参数和主要终点状态。从中可以看出，不同位置的轨迹都到达了着陆窗口。轨迹1由于飞行航程接近95.5 km，校正圆柱的位置参数xHAC调整至最近值，同时能量因子ηe由0.5迅速调整稳定至0.22左右，以应对飞行距离的增加。轨迹2相比1航程缩短了约13 km，整个飞行过程ηe保持在0.51附近，与初始值相当，位置参数xHAC调整至-14 984 m 以适应更近的初始位置，从该条轨迹的参数选择可以看出，在不受其他因素约束的情况下，轨迹参数的更新以调整地面航程为主，这有益于尽快完成校正圆柱捕获，保证纵向剖面的平缓。

随着距离进一步减小，轨迹3和4采用了跨越式转弯模式以适应初始位置的变化，在其飞行航程相当的情况下，轨迹4的参数ηe整体比3小0.4，这是由于轨迹4的初始方向偏差比3大30°，捕获转弯消耗了更多能量所致。轨迹5航程仅为71 km，在3条直接式转弯轨迹中最短，其xHAC最终更新至-21 597 m，ηe增加至0.87。对比轨迹2发现，在xHAC仍有更新空间的情况下，轨迹5的纵向参数展现了更大的更新幅度，因为初始位置在圆柱左侧时，参数更新策略需对xHAC幅值的增加起抑制作用，ηe需大幅增加以减小航程。

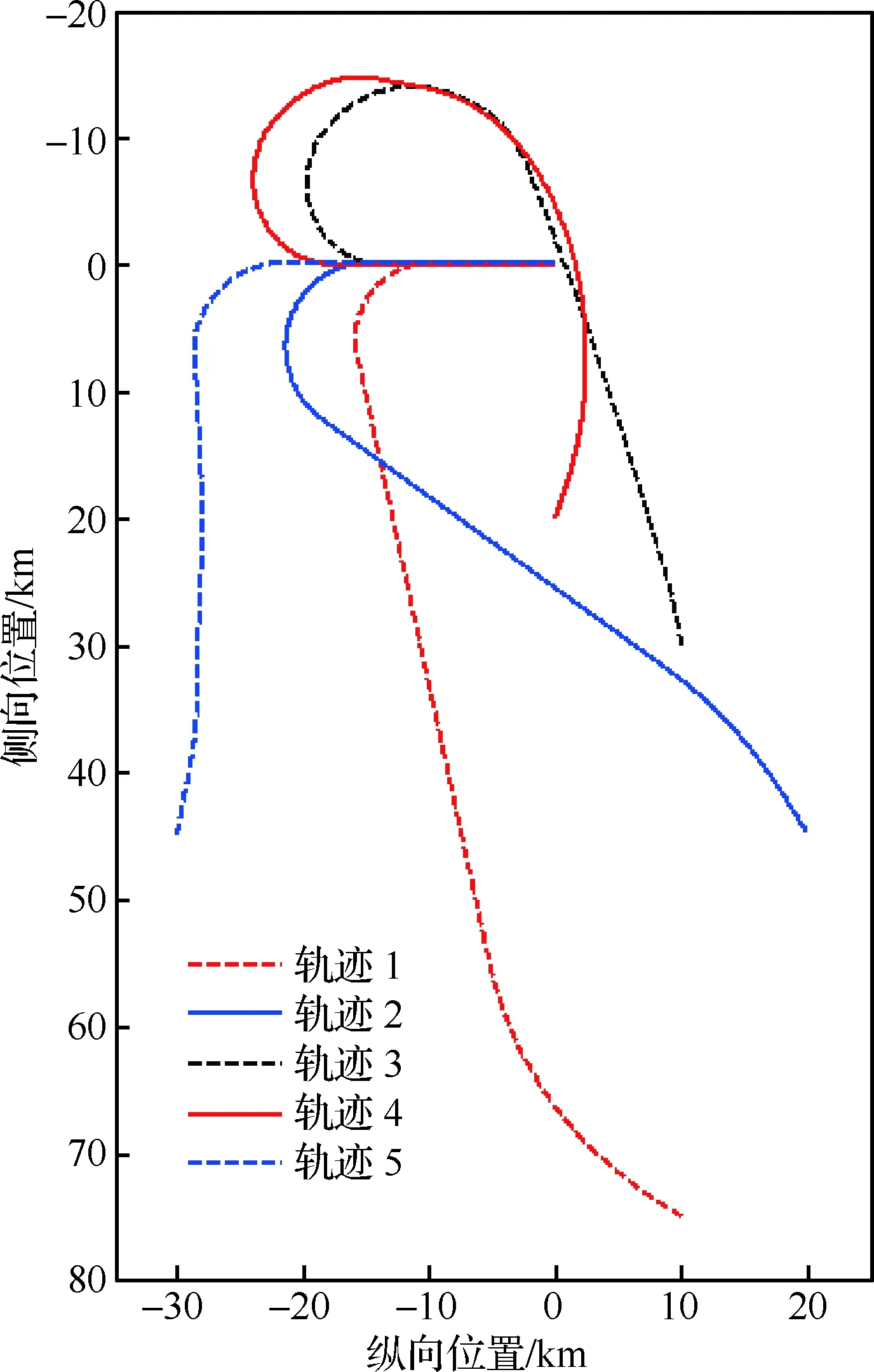
图9 位置、航向散布下的地面航迹图Fig.9 Results of ground track in position and heading angle dispersion condition

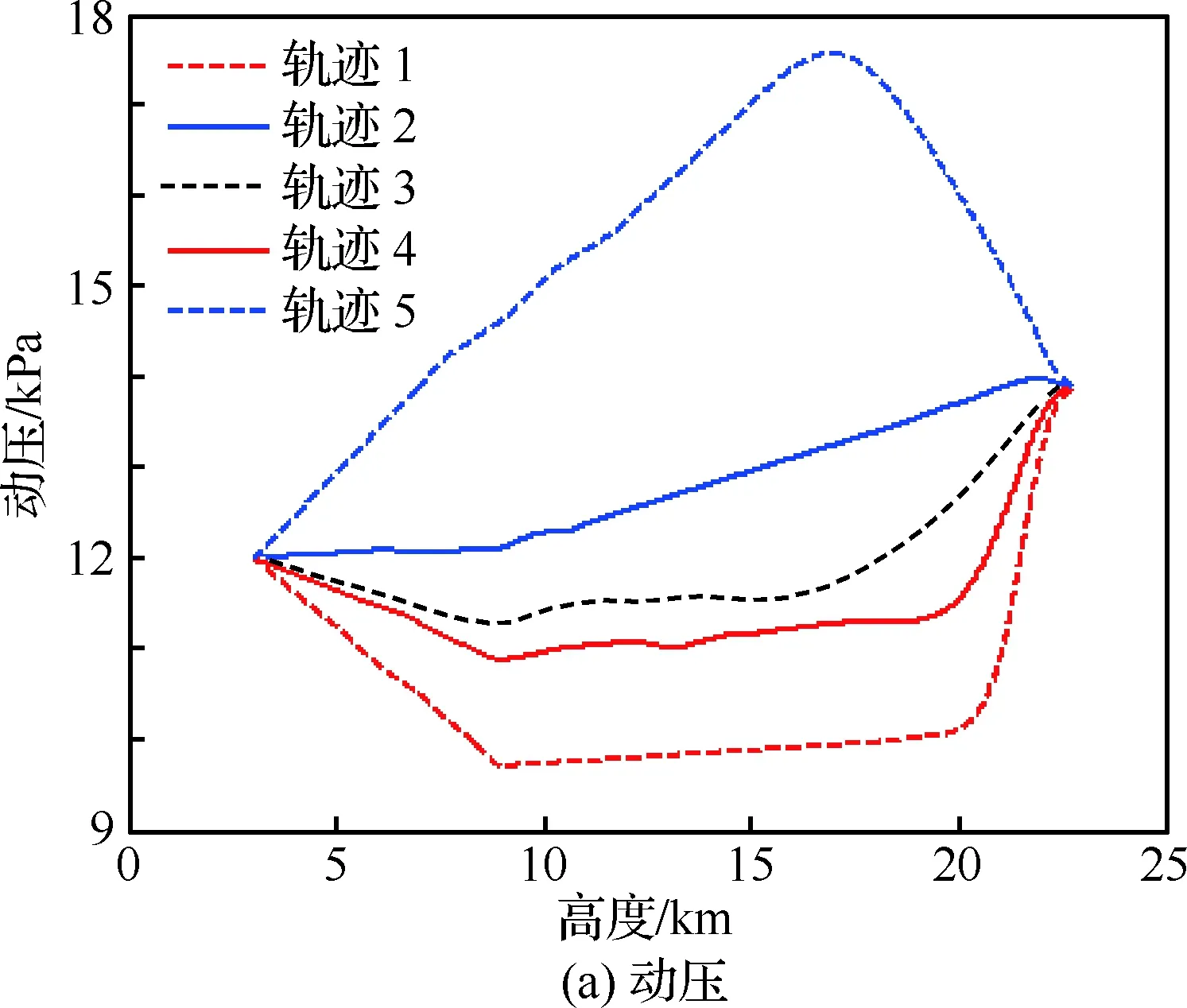
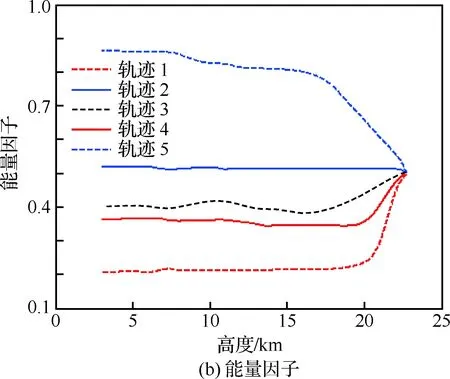
图10 位置、航向散布下的轨迹状态和参数信息Fig.10 Trajectory states and parameters in position and heading angle dispersion condition

由图10可以看出，动压的中间状态几乎覆盖动压包线，表明了制导算法较强的航程调整能力；ηe的更新过程连续光滑，保证了动压指令的平滑性；由轨迹倾角曲线可以看出，整体而言能量因子大的轨迹，其轨迹倾角更陡，以提高能量消耗率、缩短航程。同时由表2轨迹倾角的终端状态可以看出，尽管没有对其进行约束，但飞行器的轨迹倾角散布较小，在1°左右。终端纵向位置XF的偏差在1.5m以内，速度偏差小于0.01m/s。

表2位置、航向散步下的最终轨迹参数和状态

Table2Partialparametersandstatesoffinaltrajectoryinpositionandheadingangledispersioncondition

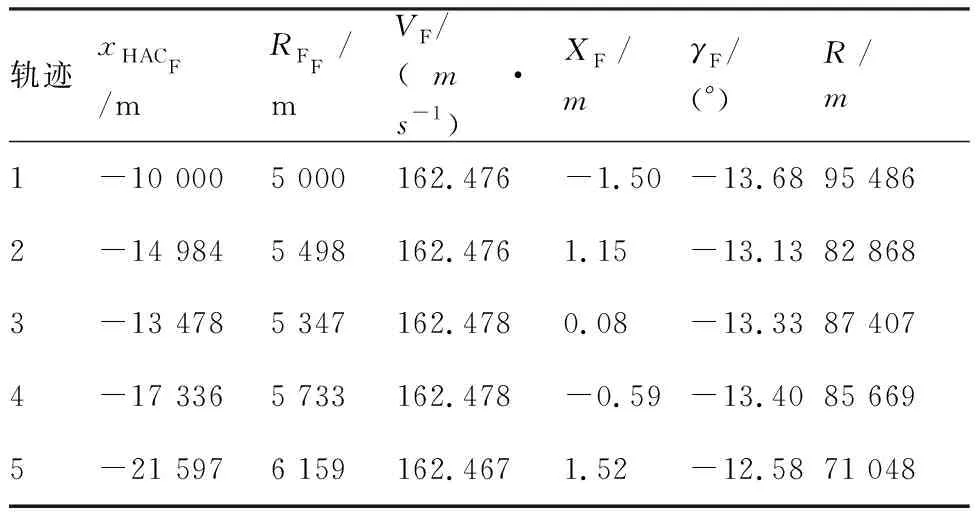
轨迹xHACF/mRFF/mVF/(m·s-1)XF/mγF/(°)R/m1-10 0005 000162.476-1.50-13.6895 4862-14 9845 498162.4761.15-13.1382 8683-13 4785 347162.4780.08-13.3387 4074-17 3365 733162.478-0.59-13.4085 6695-21 5976 159162.4671.52-12.5871 048

3.2 能量状态散布

初始条件取航向角初值ψ0=-115°，轨迹1～3 取相同初始位置X0=10 000m，Z0=30 000m， 轨迹4和5初始位置取X0=-5 000m，Z0=45 000m，其他初始条件如表3所示，可以看出轨迹1～3初始能量因子相同，而能量依次递减，轨迹4和5具有相同的初始位置和能量，仅初始能量因子不同。其他条件根据相应能量状态时的平衡滑翔条件计算。

由图11和图12可以看出，在初始位置、航向相同的情况下，不同初始能量和能量因子均对轨迹的参数产生影响。轨迹1由于初始能量取最大值47 763m，以跨越方式转弯。轨迹3能量只为最大值的1/2，这使得在同样位置条件下，不仅校正圆柱的位置调整至最近，而且能量因子由初始时的0.5调整至不足0.3以增大飞行距离。轨迹4和5由于初始能量因子不同，造成了初始高度、速度等条件的较大差异。其中，轨迹4中ηe的初值为0.2，对应了更强的飞行能力，因此其航程达到了68.8 km，xHAC调整至-161 36 m，ηe由初始值调整增加至0.3以保证校正转弯开始后轨迹具有足够的调整空间。轨迹5由于初始能量因子较大为0.8，飞行距离缩短至59.9 km，xHAC调整至最近，同时ηe大幅减小至约0.46，这使得飞行器的动压迅速减小至低能量消耗状态。

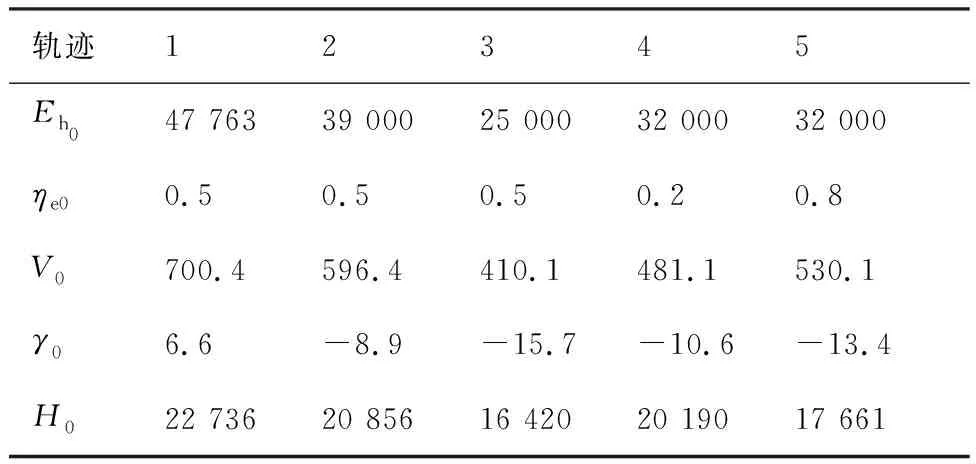
表3 初始能量条件Table 3 Initial energy conditions

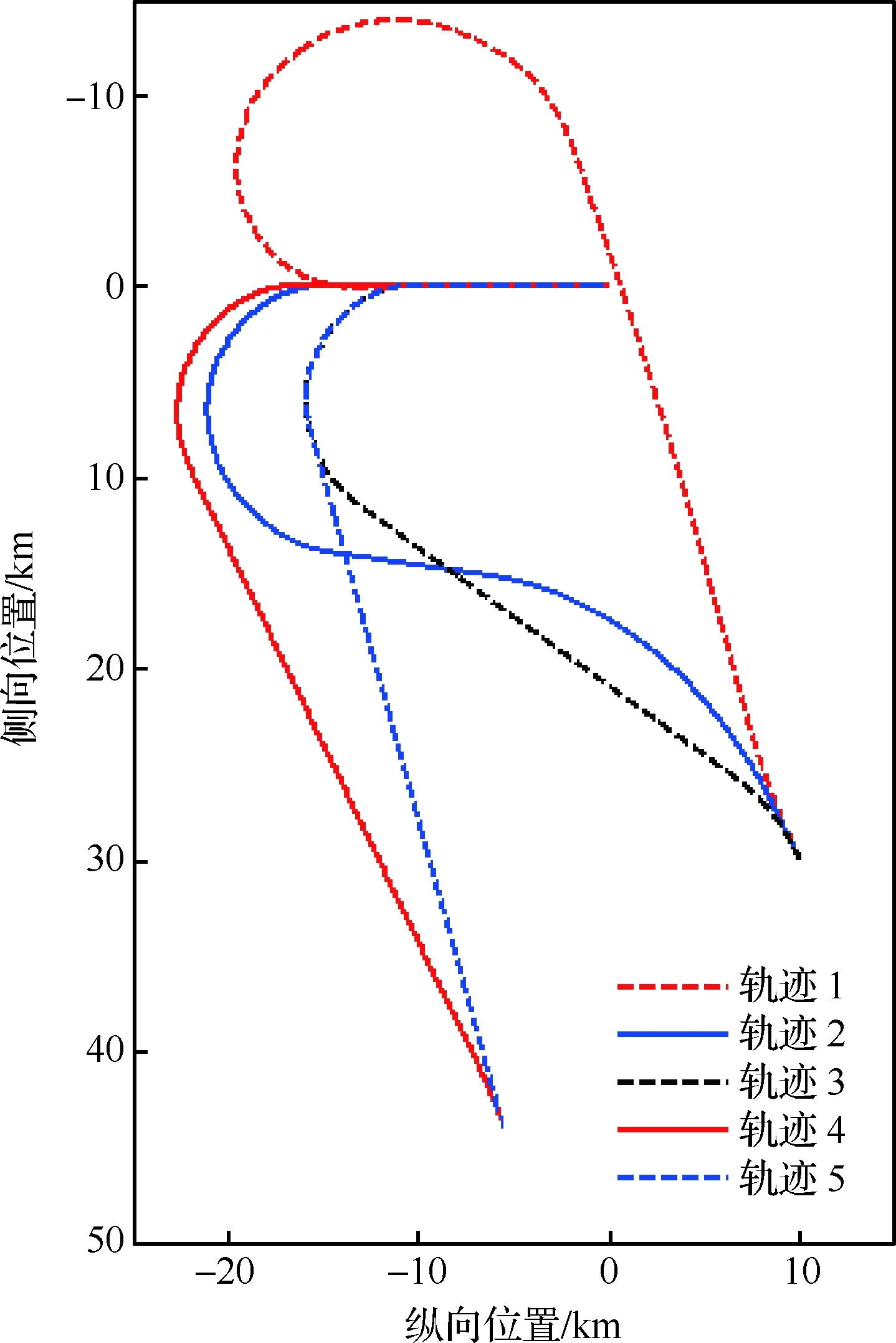
图11 能量状态散布下的地面航迹图Fig.11 Results of ground track in energy status dispersion condition

由倾侧角变化曲线可看出除曲线1因校正转弯开始时的航向偏差稍大造成倾侧角饱和外，转弯时的倾侧角用量整体小于50°，满足约束条件的要求。表4为地面轨迹最终参数和终点状态，从中可看出，相比3.1节的结果，纵向位置误差在初始能量摄动的影响下仍然保持在了米级。结合第一部分的仿真内容，将其与文献[19,21]不考虑模型偏差情况下的仿真结果对比发现，该情况下制导算法都表现出了量级相当的位置、速度精度。

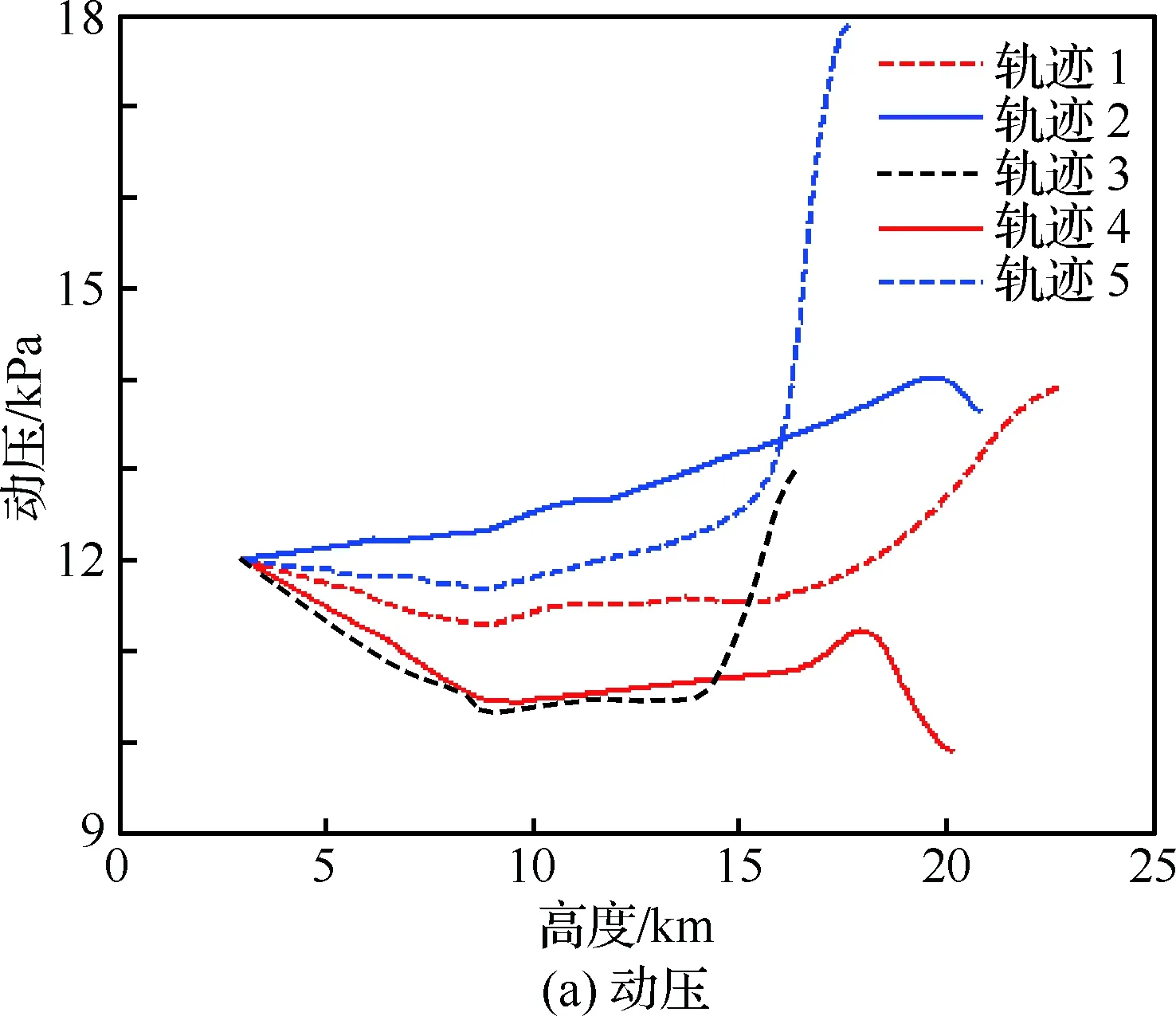
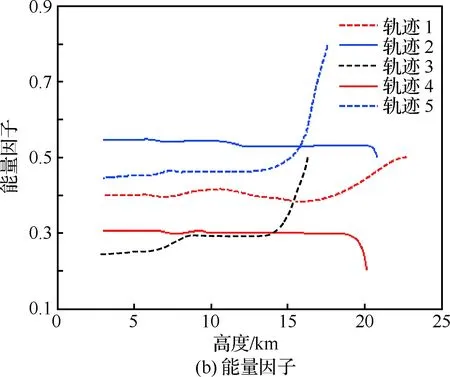
图12 能量状态散布下的轨迹状态和参数信息Fig.12 Trajectory states and parameters in energy status dispersion condition

表4 能量状态散布下的最终轨迹参数和状态

Table 4 Partial parameters and states of final trajectoryin energy status dispersion condition

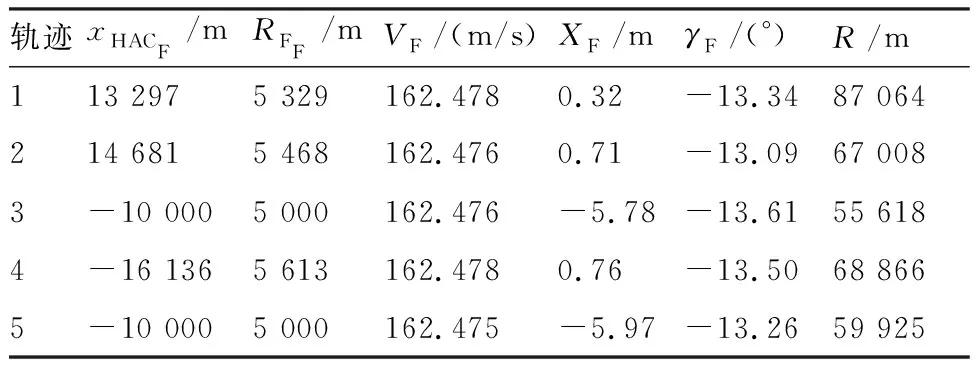
轨迹xHACF/mRFF/mVF/(m/s)XF/mγF/(°)R/m113 2975 329162.4780.32-13.3487 064214 6815 468162.4760.71-13.0967 0083-10 0005 000162.476-5.78-13.6155 6184-16 1365 613162.4780.76-13.5068 8665-10 0005 000162.475-5.97-13.2659 925

3.3 突发故障测试和计算效率分析

为综合验证制导算法的高效性和对于突发故障的适应能力，本小节对2种典型的故障模式进行了测试，并将故障状态的轨迹与标称条件下的结果进行了对比。随后，对上述3条轨迹的仿真时长和实际耗时进行了统计，进而估算出单次轨迹预测的实际用时，将其与数值积分预测的效率进行了比较。

仿真的初始条件与3.1节中轨迹2相同。为使对故障状态的描述具有一般性，这里并不详述故障形成的原因，而只给出故障产生后气动模型的外部变化(升力、阻力改变)。两种故障模式的详细信息如表5所示。表中，tb和tr分别表示故障发生和恢复的时刻，表格第3列则给出了故障发生后的模型偏差量。从表中可以看出，故障的发生引起了阻力系数的大幅增大和升力系数的损失，两种故障模式的区别在于模式1的故障发生的时间较早，且于50 s后从故障状态恢复，模式2则发生在轨迹的中末段，并且持续至飞行结束。为增加故障模式的真实性，同时测试制导算法对于大气偏差影响下的性能，该组仿真采用了某试验场地3月份实测大气模型。

表5 两种故障模式的参数Table 5 Parameters of two failure modes

故障模式与标称轨迹的结果对比如图13和图14 所示。其中，图13为3种情形的地面航迹图。可以看出，制导算法针对模式1的故障进行了两次地面航迹的较大调整以适应模型参数的变化；模式2的故障发生于校准转弯过程中，此时地面航迹无法进行调整，因此具有与标称状态具有几乎相同的航迹。图14则分别反映了不同故障模式下动压、航迹倾角、纵向和侧向轨迹参数的调整过程。从中可以看出，开始阶段，制导算法迅速调整轨迹参数以消除初始的航程偏差，此时3种情况具有相同的飞行状态。高度为19.7 km时，模式1的故障发生，造成飞行能力下降，制导算法快速感知模型变化，将ηe小幅减小至0.48，而xHAC则大幅移动至-11.7 km处以缩短地面航迹，这使得此后飞行动压相比较标称动压平均减少约0.5 kPa，航迹倾角则由于模型的变化而逐渐变陡。高度降至14 km时，模式1的故障消除，此后制导算法进行了第2次较大幅度的参数调整，将ηe增大至0.53，xHAC增大至-13.7 km，此时动压持续上升，并在之后的过程中始终大于动压标称值。模式2的故障发生在高度11 km时，由xHAC的更新历程可以看出，此时侧向参数已停止更新，航程的调整只能通过减小ηe实现。由ηe的变化曲线可以看出，由于高度接近末端状态，动压可调整空间逐渐缩小，ηe更新幅度显著增大，其值由0.51大幅降至0.15后又持续减小直至在末端达到极限最小值。ηe的大幅更新同样引起了动压和航迹倾角的剧烈变化，其中动压由12.3 kPa急速降低至9 kPa，后在末端动压约束下逐渐收敛至12 kPa，期间则造成了航迹倾角约8°左右的波动。

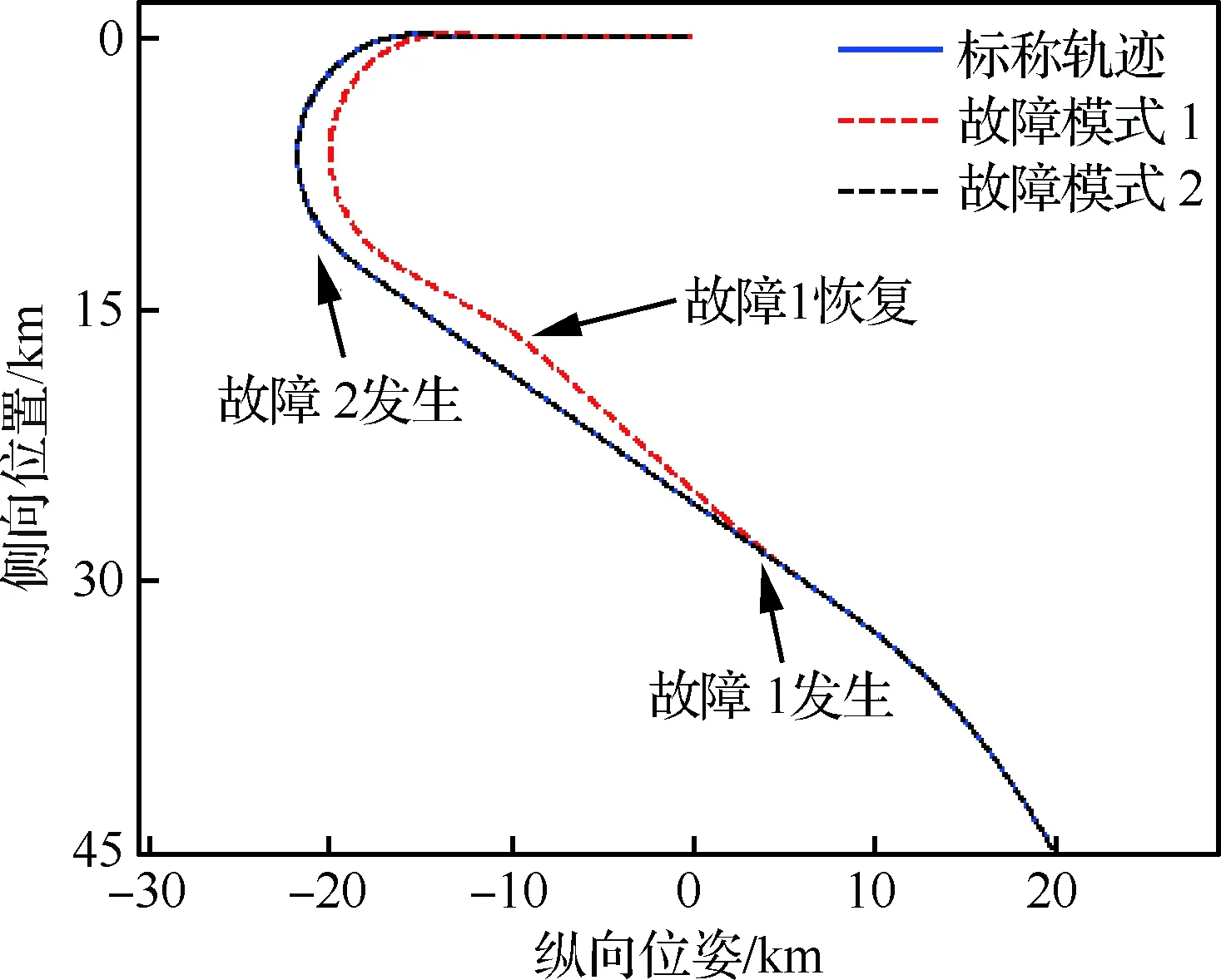
图13 故障模式下的地面航迹图Fig.13 Results of ground track of failure mode

表6给出3条轨迹的末端主要状态、仿真时长与实际耗时的结果。其中，由末端位置的结果可以看出，故障模式1对末端位置精度几乎未造成影响，其与标称状态的位置偏差都在-12 m左右，该偏差是由大气模型偏差造成的。而故障模式2由于条件更恶劣末端位置偏差达到-85.5 m，末端航迹倾角γF则与标称状态相差2.7°，这是由三项模型偏差累积且轨迹参数达到极限造成。在文献[4]经典的航天飞机制导中，要求末端位置偏差绝对值小于30 m，高度偏差小于100 m，速度偏差小于15 m。可以看出，考虑仿真结束条件不同的因素，即使对于条件最恶劣的故障模式2，其综合性能仍大幅高出经典方法的精度指标。同时，由该部分仿真结果可以看出，本文的在线制导算法能够在未获得故障信息和模型参数各项偏差的情况下，及时对突发故障(或故障恢复)后的飞行器轨迹进行在线调整，这种能力是传统制导方法所不具备的。

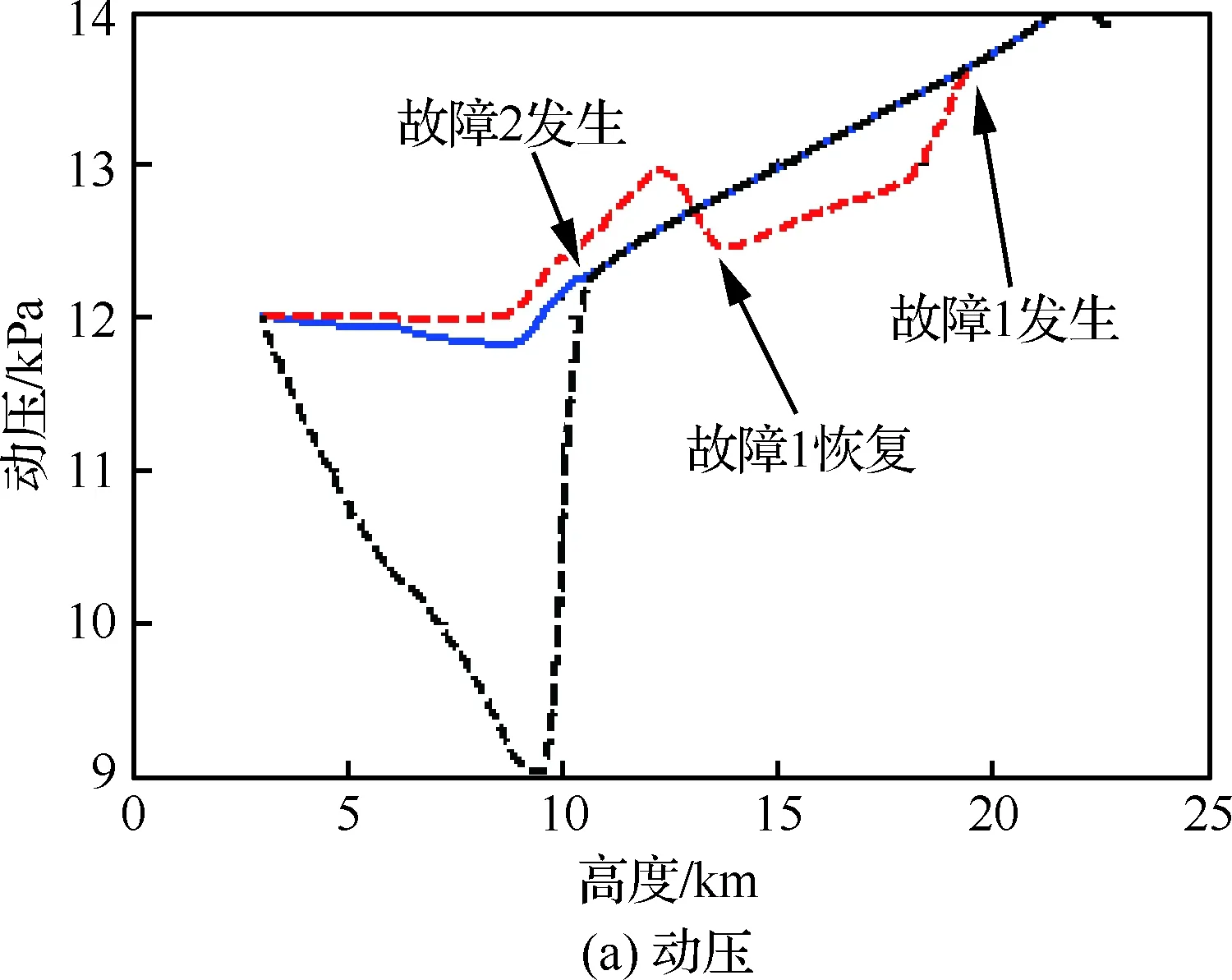
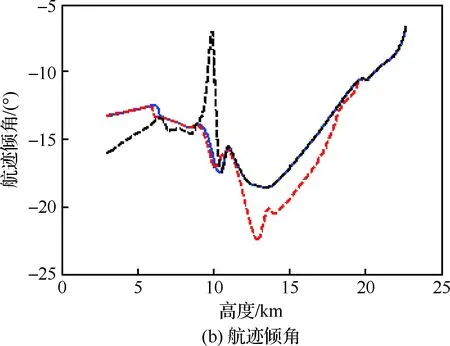
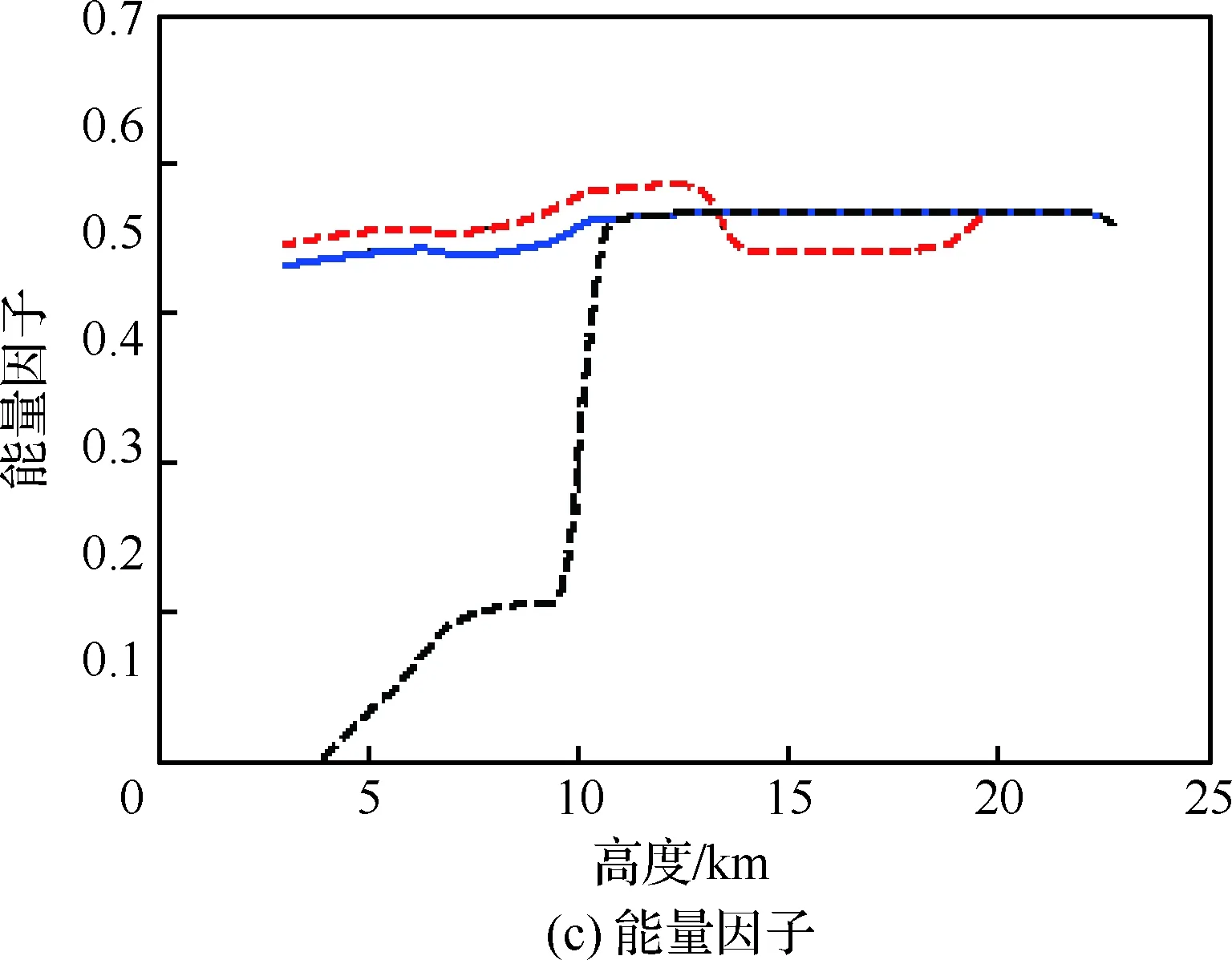
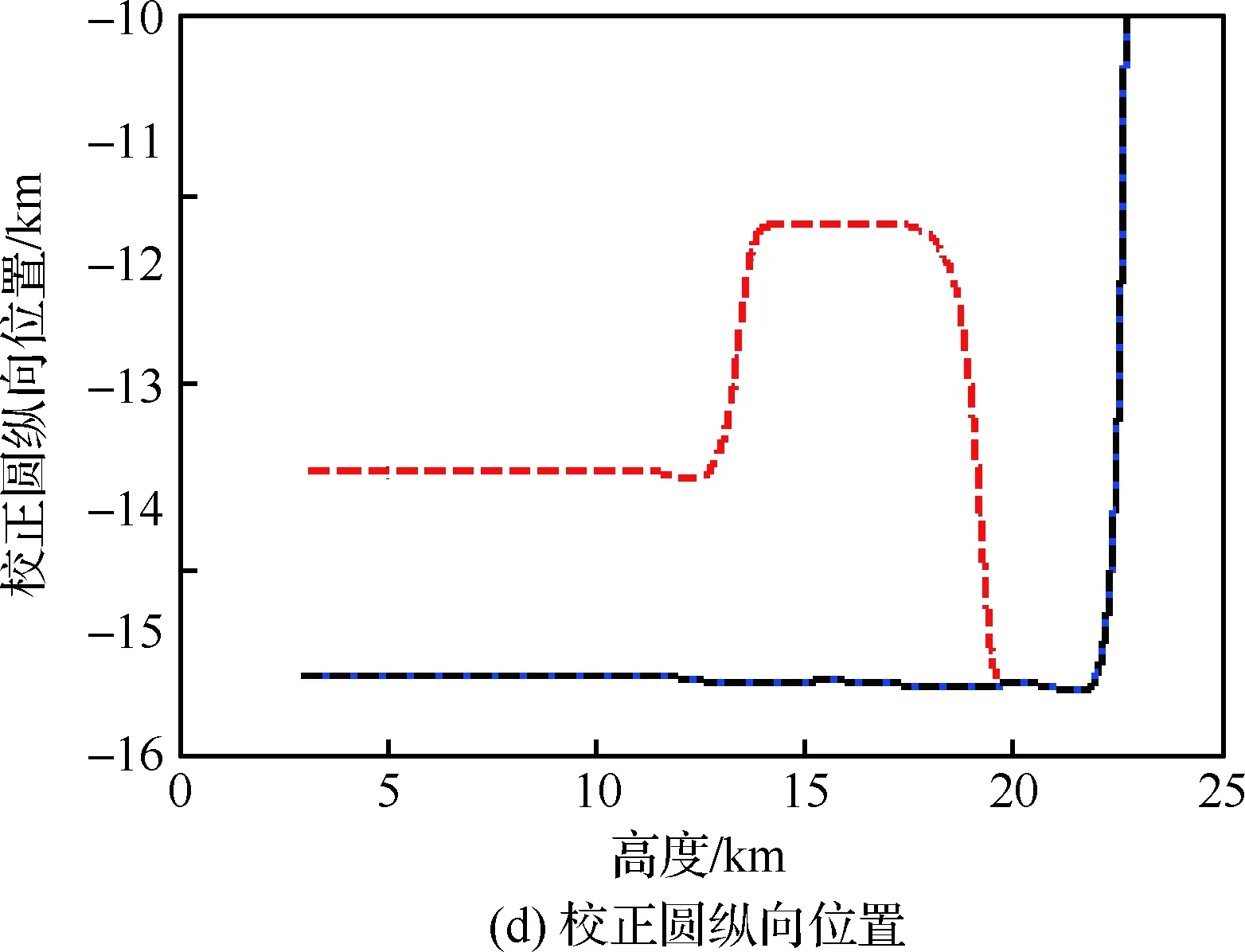
图14 故障模式下的轨迹状态和参数信息Fig.14 Trajectory states and parameters of failure mode

制导算法的预测效率是评价算法性能的重要指标。由于本文制导算法与运动模型整体构建于SIMULINK仿真平台中，单次轨迹预测-更新的用时难以直接获得，这里通过如下公式进行估算：

tpre=Tutcsm/tsim

(52)

式中：tpre为单次轨迹预测-更新的计算用时；tcsm为仿真实际耗时；tsim为仿真时长；Tu=0.02 s为文中设定的参数更新周期。将表6中的数据代入式(52)，可知3条轨迹的tpre均在2.3 ms左右。对比采用在线数值积分预测方法且在计算效能分析中使用了与本文性能相似的仿真计算机的文献[18]，其完成一次轨迹预测的平均用时为0.55 s， 最大时长为0.95 s，本文的计算效率相比其高出两个数量级，这为本文通过连续预测消除航程偏差和快速应对突发故障提供了性能支撑。

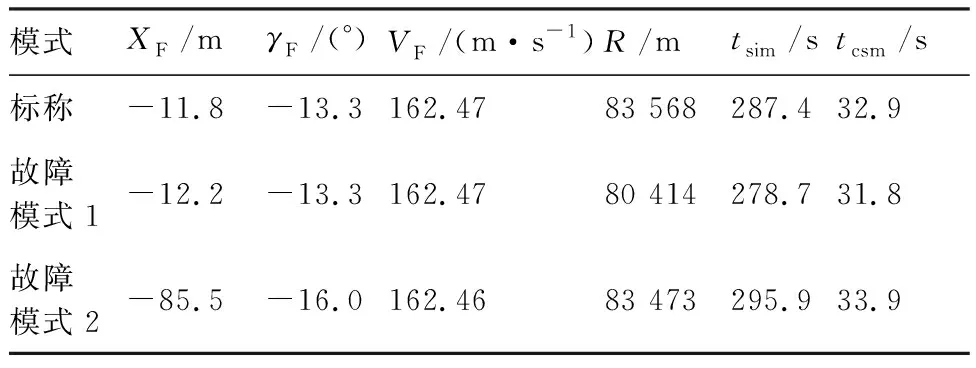
表6 故障模式的最终状态和计算效率

4 结 论

1) 本文提出的基于分段查表预测与在线观测修正相结合的在线制导算法在轨迹预测的速度上相较数值积分预测方法高出一个数量级以上，轨迹预测的效率得到了大幅提升。

2) 由于考虑了侧向机动的额外能量消耗和通过在线观测对模型偏差引起的航程变化进行了修正，使得查表预测的精度大幅提高，对初始位置、航向和能量的大幅变化不敏感，对突发故障具有较快的反应速度和适应能力。

3) 提出的约束条件下多轨迹参数更新策略解决了更新参数的匹配问题，在增强了轨迹调整能力的同时保证了参数更新的余量和轨迹的适宜性。其不足之处在于权重的选取依赖于经验，基于优化方法的参数更新算法是下一步研究的内容。

4) 由于没有对末端航迹倾角进行约束，在模型偏差情况下该状态量出现了较大散布，且本文算法末端轨迹调整能力减弱，造成轨迹参数更新在极端故障模式下出现饱和，航程偏差不能持续消除。该问题将在今后的研究中通过一体化的能量管理段和着陆段轨迹生成与制导方法解决。