GH4169合金蠕变疲劳行为的有限元模拟及寿命预测

姚萍，王润梓，郭素娟，张显程

华东理工大学 承压系统与安全教育部重点实验室，上海 200237

涡轮盘等航空发动机关键部件，在服役过程中，不仅承受着飞机起落和飞行速度波动造成的循环载荷，也承受着伴随发动机稳态运行而产生恒定应力、温度载荷，其损伤来源于疲劳、蠕变及两者间的交互作用[1-4]。研究表明，材料在蠕变-疲劳交互作用下的寿命远低于其在单一蠕变或疲劳机制下的寿命[5-6]。因此，实现对涡轮盘组成材料在蠕变-疲劳共同作用下准确的寿命预测十分必要。

在实际应用中，加载历史对部件及材料寿命的影响至关重要，因此通过有限元方法，获取构件材料在蠕变-疲劳服役过程中的实时应力、应变状态，继而结合合理的损伤预测模型，监测涡轮盘组成材料在每一周次的蠕变-疲劳损伤响应，是获取其当前状态和剩余寿命的有效手段之一[7-8]。这一过程的实现，主要依赖于能合理描述材料在蠕变-疲劳交互作用下的循环变形行为的本构模型和基于逐次损伤的概念的蠕变-疲劳损伤预测模型。在本构模型方面，目前国内外大量的研究表明：组合非线性随动强化演化准则(如Chaboche模型等)和各向同性强化演化准则的循环弹塑性本构模型可以合理描述构件材料在蠕变-疲劳服役过程中加/卸载阶段的循环变形行为[9-10]；基于时间强化和应变强化的蠕变本构模型，可以对构件材料在应力/应变保载阶段的蠕变行为和应力松弛行为得到较好的描述[11]。在蠕变-疲劳寿命预测模型的研究方面，Robinson[12]提出的时间分数法提供了以应力和时间作为蠕变损伤的度量，Hales等[13-14]基于时间分数法发展出了延性耗散模型，上述模型结合线性累积损伤准则已在机械、船舶等行业的蠕变-疲劳寿命评估中得到了较为广泛的应用。近期，Skelton[15]和Takahashi[16]以应变能密度耗散率和失效应变能密度为参量，Wang和Zhang[17]则在此基础上纳入平均应力效应和Jeong等[18]提出的应力松弛经验公式，提出和发展了新的应变能密度耗散模型，进一步提高了蠕变-疲劳寿命预测的整体精度。然而，上述模型均建立在材料半寿命或稳态循环周次的应力、应变状态之上，并没有考虑损伤参量随循环周次的演化过程。目前，基于逐次损伤的概念对部件及材料进行蠕变-疲劳寿命预测的相关研究非常少见[19]。

针对上述研究背景和现状，本文选取航空涡轮盘常用材料GH4169镍基合金为研究对象，基于ABAQUS有限元软件和已有实验结果[19]，首先采用组合Chaboche随动强化准则[10]和Voce各向同性硬化准则[20]的循环塑性模型，叠加应变强化蠕变模型，实现了对该合金蠕变-疲劳过程中应力、应变状态的准确描述。后将Wang和Zhang[19]提出的基于逐周次概念的应变能密度耗散模型进行了有限元实现，基于有限元模拟所得的循环应力、应变状态，对GH4169合金每个周次的蠕变-疲劳损伤进行实时监测，进而预测了其蠕变-疲劳寿命，并与实验结果相比较验证了预测结果的准确性。研究结果为进一步实现对涡轮盘等关键部件精确的蠕变-疲劳寿命预测奠定了坚实的基础。

1 本构模型和寿命预测模型介绍

1.1 本构模型

研究表明，Chaboche非线性随动强化演化方程可以合理描述材料在循环变形过程中的内应力的非线性演化过程[10]，而Voce非线性各向同性演化方程则可实现对循环软/硬化过程的描述[20]。因此，本文通过ABAQUS大型有限元软件模拟GH4169合金蠕变-疲劳载荷下的循环变形行为时，采用组合Chaboche非线性随动强化演化方程[10]和Voce非线性各向同性强化演化方程[20]的弹塑性循环本构模型，叠加能够合理描述该类材料应变保载下的非线性应力松弛行为的应变强化蠕变模型[21]来实现。本文主要描述GH4169合金在650 ℃下的蠕变-疲劳行为，因此本构模型中并未考虑温度参数，而是采用基于该温度实验所确定的参数来反映温度相关性。具体本构方程介绍如下：

1.1.1 弹塑性循环本构模型

为了合理描述GH4169合金在蠕变-疲劳加载条件下加/卸载过程中的循环软化行为[19]，弹塑性循环本构方程选用组合非线性随动强化和各向同性强化的形式，其中Chaboche非线性随动强化演化方程为[10]

(1)

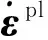
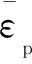
(2)

式中：Q0为初始屈服应力；Q∞为屈服面尺寸改变的极限值；b为屈服面的尺寸随塑性应变增加的变化率。Q∞小于零表示为循环软化材料。

1.1.2 应变强化蠕变本构模型

为了描述GH4169合金在应变峰值保载阶段的非线性应力松弛行为，在循环变形的基础上叠加了应变强化的蠕变本构模型。经过验证，应变强化的蠕变本构模型能够合理描述该类材料第一阶段和第二阶段的蠕变和松弛行为，相关蠕变应变率可表示为[11]

(3)

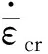
1.2 寿命预测模型

对构件的蠕变-疲劳寿命预测主要是基于对其蠕变-疲劳损伤的预测，本文在进行蠕变-疲劳寿命预测时采用了Wang和Zhang[19]提出的基于逐周次概念的应变能密度耗散损伤模型。该模型将蠕变-疲劳损伤分解为疲劳损伤和蠕变损伤两部分进行预测，现将具体疲劳损伤和蠕变损伤的计算方法简述如下：

1.2.1 疲劳损伤

疲劳损伤的计算采用的是Ostergren[21]提出的基于净拉伸滞后能参数的损伤模型，该损伤模型借助应变能耗散的概念，考虑了平均应力效应的影响。同时，模型通过对单个周次疲劳损伤的逐次引入，考虑了疲劳失效过程中疲劳损伤的逐周次累积，其损伤方程为

(4)

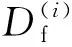
1.2.2 蠕变损伤

在蠕变损伤的计算方面，Wang和Zhang模型[19]通过引入平均应力[22]，并结合Jeong等[18]提出的把应力松弛与塑性应变范围和保载时间相关联的概念，对Takahashi提出的应变能密度耗散模型[16]进行了进一步修正，同时还将逐周次计算损伤[14]的概念考虑在内，最终得到的基于逐周次概念的蠕变损伤方程为

(5)

其中：

(6)

(7)

(8)

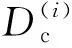
2 GH4169合金蠕变-疲劳载荷下循环变形行为的有限元模拟

GH4169合金是一种沉淀强化的镍基高温合金，该材料具有良好的综合性能，特别是在高温下有较强的强度和组织稳定性，主要用于涡轮盘等航空发动机部件。文献[19]采用圆棒试样对GH4169合金开展了应变控制的蠕变-疲劳实验研究。实验过程中应变比R=-1，加/卸载阶段的应变速率为0.4% s-1，实验温度650 ℃。本节主要采用大型有限元软件ABAQUS，在650 ℃高温下，对GH4169合金在蠕变-疲劳载荷下的循环变形行为进行合理的有限元模拟，为后文基于逐周次概念的蠕变-疲劳寿命预测提供逐周次的应力、应变状态。

2.1 加载工况和有限元模型介绍

根据实验加载工况[19]，采用图1所示的蠕变-疲劳加载波形，分别取应变范围为2.0%，1.6%和1.4%，保载时间为60、120、300和1 800 s等情况开展GH4169合金蠕变-疲劳行为的有限元模拟。由于实验过程中载荷谱通过引伸计控制试样工作段的应变来施加，为了更方便的确定载荷和边界条件，有限元模拟仅针对圆棒试样的工作段进行建模。考虑到圆棒试样的轴对称特性，建立如图2所示的1/4轴对称有限元模型，模型选用四边形轴对称单元进行网格划分。具体的边界条件和加载方式为：在沿模型的中心轴AB的所有节点上施加X方向的对称约束；在沿AD端面的所有节点上施加Y方向上的对称约束。BC端为加载端，将循环应变转换为相应的Y方向的循环位移进行施加。

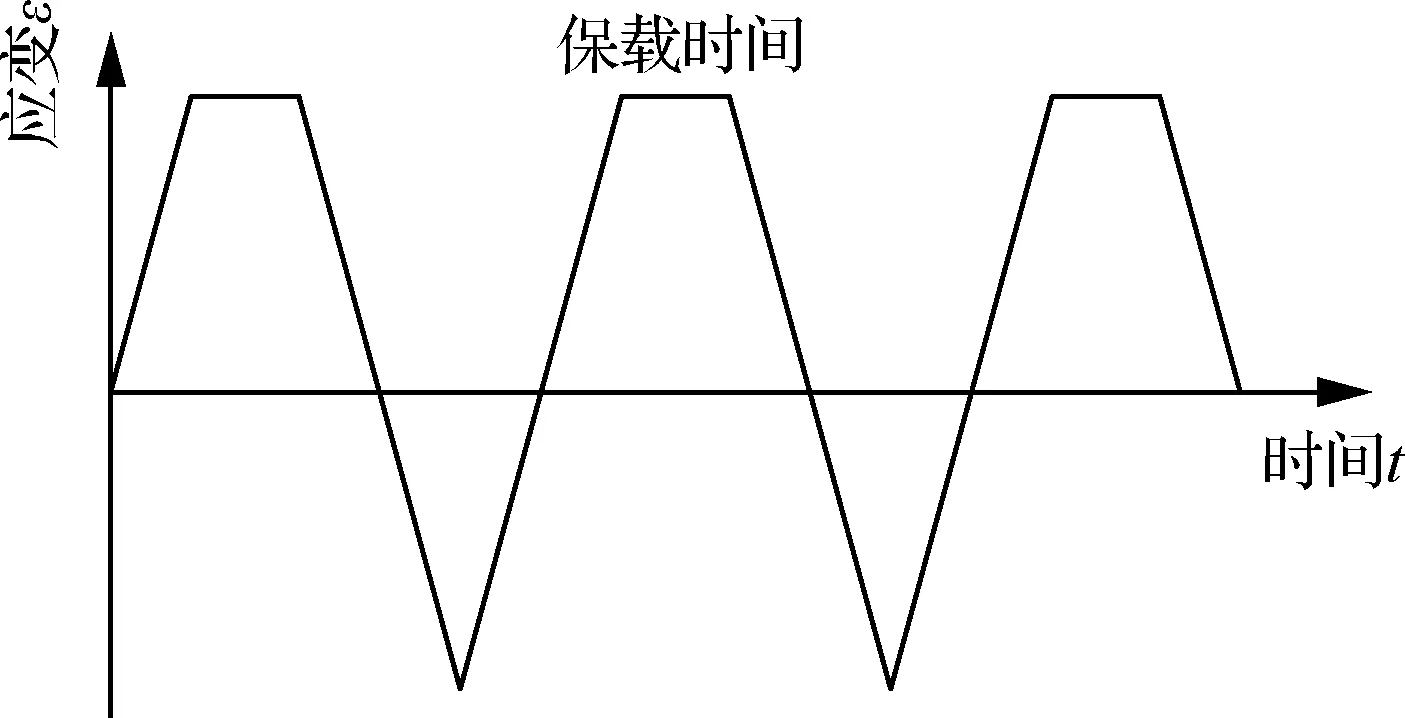
图1 蠕变-疲劳载荷谱Fig.1 Creep-fatigue loading spectrum

图2 蠕变-疲劳试样工作段的有限元网格Fig.2 Finite element mesh of working section of creep-fatigue specimens

2.2 材料参数确定

2.2.1 Chaboche模型参数确定

实验测得GH4169合金在650 ℃高温下的弹性模量为171 GPa，泊松比0.3，初始屈服强度Q0为835 MPa[19]。Chaboche非线性随动强化演化方程的相关参数可根据文献[10]的方法，通过GH4169合金的高温单轴拉伸应力-应变曲线确定，可得：C1=408 590 MPa，γ1=2 000，C2=11 000 MPa，γ2=50，C3=30 MPa，γ3=1。采用上述参数模拟GH4169合金单轴拉伸应力-应变曲线，模拟结果与实验结果[19]如图3所示，可见二者符合得非常好。

此外，为了更明确地显示模拟结果与实验结果的接近程度，在模拟GH4169合金的单轴拉伸、应力松弛和蠕变-疲劳行为时，将引入统计学相关系数R进行相关性比较。相关系数R是用以反映两组数据之间相关关系密切程度的统计指标，当R=1时，表明两组数据完全相关，而R越接近1，两组数据的相关程度越大，其计算公式为

(9)

式中：X和Y分别表示各工况模拟和实验曲线中各数据点的值；N表示数据点个数。计算可得GH4169合金的单轴拉伸应力-应变曲线的模拟结果与实验结果相关性系数为R=0.999 8。

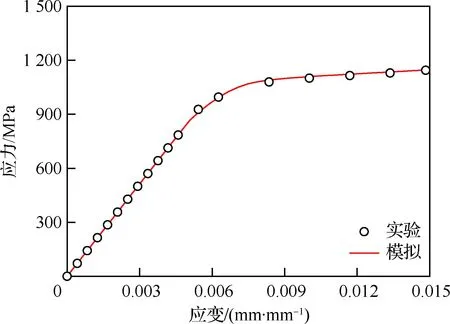
图3 GH4169合金的单轴拉伸应力-应变曲线 Fig.3 Uniaxial tensile stress-strain curve of GH4169 alloy

2.2.2 应变强化蠕变模型的相关材料常数确定

应变强化蠕变本构模型相关参数，主要包括ψ、n和m。采用图2的有限元网格，模拟GH4169合金在应变保载值Δεt=2.0%，保持时间为1 800 s时应力松弛行为，同时采用逐步优化的方法，最终确定ψ、n和m的值。首先，分析ψ值对应力松弛曲线的影响，此处暂时随机选取n=5.84，m=-0.62。图4(a)为模拟所得的应力松弛曲线与实验曲线[19]的比较，从图4(a)中可以看出，ψ的改变对应力松弛初期的松弛速率有较大影响，当ψ=5.823 1×10-23时，模拟所得初期应力松弛速率与实验最为一致。然后，为了进一步获取合理的n值，取ψ=5.823 1×10-23，m=-0.62，针对不同的n值对GH4169合金的应力松弛行为进行有限元模拟，所得模拟结果如图4(b)所示，从图中可以看出，当n=5.77时，模拟应力松弛曲线在前400 s与实验最为接近，故取n=5.77。最后，通过优化m值，实现对材料应力松弛行为更进一步的合理描述，模拟结果如图4(c)所示。从图中可以看出当m=-0.72时，模拟结果与实验结果符合得很好，其相关性系数R=0.995 1。综上，最终可得ψ=5.823 1×10-23、n=5.77和m=-0.72。

由于上述参数仅仅是根据一种实验工况(应变范围为2%)确定的，为了验证参数针对不同载荷工况的有效性，基于上述参数值和图2所示的有限元模型，模拟GH4169合金分别在应变范围为2.0%、1.6%和1.4%的蠕变-疲劳载荷下，第一周峰值应变保载过程中的应力松弛曲线(保载时间分别为1 800 s和300 s)，模拟结果和实验结果[19]的比较如图5所示。可见模拟结果与实验结果符合得非常好，根据式(9)计算可得应变范围为2.0%、1.6%和1.4%的相关性系数R分别为0.994 0、0.946 1和0.899 6，相关性较高，说明采用应变强化的蠕变本构模型和上述参数值，可以合理的描述GH4169合金峰值应变保载过程中的应力松弛现象。

艺术家的“文化人”身份首先意味着艺术家是了解和掌握了哲学、宗教、科学、技术、文学、社会心理、民间风俗相关知识和信息的人。哲学、宗教、文学和民俗风情等启迪艺术家的创作；艺术创作中又体现着哲学、宗教、文学和民俗风情。

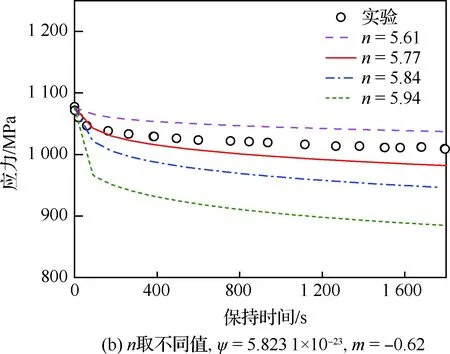
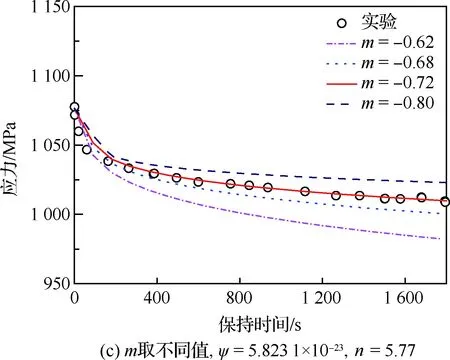
图4 第一周峰值应变保载过程中的应力松弛演化曲线(Δεt=2.0%)Fig.4 Evolution curves of stress relaxation process during peak strain hold period in the first cycle (Δεt=2.0%)

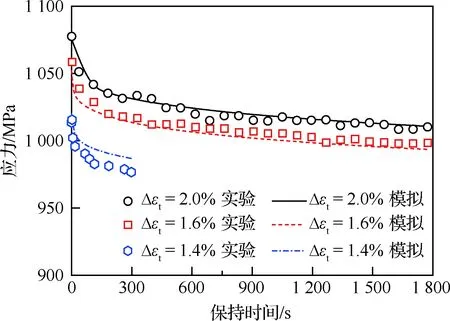
图5 第一周峰值应变保载过程中的应力松弛演化曲线Fig.5 Evolution curves of stress relaxation process during peak strain hold period in the first cycle

2.2.3 Voce非线性各向同性演化方程的参数确定

GH4169合金的循环软化过程主要受到循环软化程度和软化速率两个因素的控制。Voce非线性各向同性演化方程的相关参数包括Q∞和b，其中，Q∞反映循环软化过程中的循环软化程度，b则反映循环软化速率。针对上述参数意义，采用图2所示的有限元网格，2.2.1和2.2.2小节所确定的Chaboche随动强化演化方程和应变强化蠕变模型的相关材料参数，模拟GH4169合金的循环软化过程，同时结合参数优化法，确定最终的参数Q∞和b。模拟时选取应变范围为2.0%，保持时间为1 800 s，应变比R=-1的蠕变-疲劳工况。首先，通过优化获取合理的Q∞值，实现对材料蠕变-疲劳过程中循环软化程度的合理描述。由于b的值只影响循环软化速率，对循环软化幅度没有影响，此处随机暂取b=1.6。图6(a)给出了b=1.6时，采用不同的Q∞值对GH4169合金的蠕变-疲劳过程进行有限元模拟，所得的最大应力随循环周次的演化曲线及其实验值[19]。图6(a)表明，b不变的情况下，Q∞越大，模拟所得的GH4169合金软化幅度越大，当Q∞取-210 MPa时，模拟所得的循环软化幅度与实验基本一致，故取Q∞=-210 MPa。此外，图6(a)中还可以看出，尽管Q∞取-210 MPa时实现了对GH4169合金循环软化程度的合理描述，但是在软化初期，随机选取的b=1.6，无法合理描述材料软化速率，模拟所得的循环软化速率低于实验值。对此，选定Q∞=-210 MPa，采用不同的b值(0.6～4.6)进行有限元模拟，所得的GH4169合金蠕变-疲劳过程中最大应力随循环周次的演化曲线与实验曲线的对比如图6(b)所示。从图6(b)可以看出，当Q∞保持不变时，b值越大模拟所得的材料循环软化速度越快，当b=2.6时，模拟结果与实验结果[19]符合得比较好，通过式(9)计算可得相关性系数R=0.978 4。根据上述分析过程和比较结果可确定，取Q∞=-210 MPa和b=2.6时，模型对GH4169合金循环软化的描述最为合理。

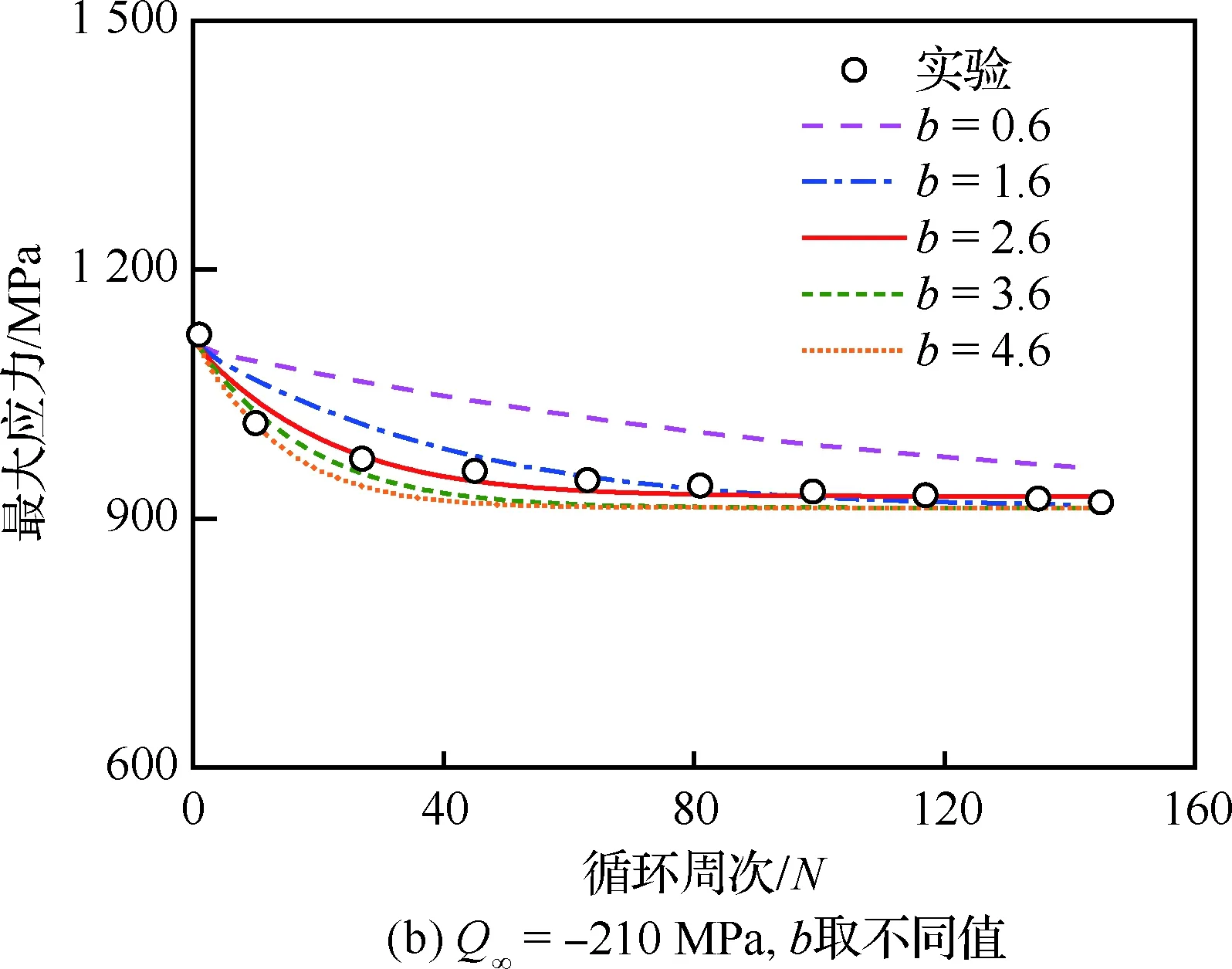
图6 最大应力随循环周次的演化曲线(Δεt=2.0%)Fig.6 Curves of evolution of the maximum stress with cyclic number(Δεt=2.0%)

2.3 模拟结果与讨论

根据应变范围为2.0%，保持时间为1 800 s，应变比R=-1的蠕变-疲劳工况，确定了本文所采用的循环本构模型涉及到的所有参数。为了进一步验证本构模型和参数对不同载荷工况的有效性，本节分别取应变范围为2.0%、1.6%和1.4%，保载时间为1 800 s和300 s，模拟GH4169合金的蠕变-疲劳过程。图7给出了不同载荷水平和保持时间下，GH4169合金蠕变-疲劳第一周次的应力-应变滞回曲线的有限元模拟结果和实验结果[19]。从图中可以看出，应变水平越低，GH4169合金的蠕变-疲劳滞回曲线越窄，且有限元模拟结果与实验结果符合得非常好。计算可得应变范围为2.0%、1.6%和1.4%的相关性系数R分别为0.940 2，0.946 1和0.991 5，说明叠加1.1节所介绍的弹塑性循环本构模型和应变强化本构模型，采用2.2节所确定的材料参数，可以合理描述GH4169合金在不同应变水平和保载时间下的应力-应变滞回曲线。

在应变控制的蠕变-疲劳载荷下，是否能准确描述最大应力随循环周次的演化是检验本构模型合理性的重要标准。由于图6在进行参数确定时，已经验证了采用最终确定的所有参数，有限元方法模拟应变范围为2.0%，保载时间为1 800 s的加载条件所得的GH4169合金最大应力-循环周次的演化曲线的合理性。为了进一步验证本文选取的本构模型和针对本构模型所确定参数的在描述GH4169合金蠕变-疲劳行为方面的有效性，本文将继续给出模型对应变范围为1.6%和1.4%，保载时间为1 800 s和300 s两种载荷工况下最大应力-循环周次的演化曲线的模拟结果，如图8所示。从图8可见，随着循环周次的增加，GH4169合金的最大应力均呈下降趋势，与相应的实验结果[19]相比，计算所得应变范围1.6%和应变范围1.4%的相关性系数R分别为0.953 7和0.891 6，本文所选取的本构模型，可以合理描述GH4169合金在不同应变范围，不同保载时间的蠕变-疲劳载荷下的循环软化行为。

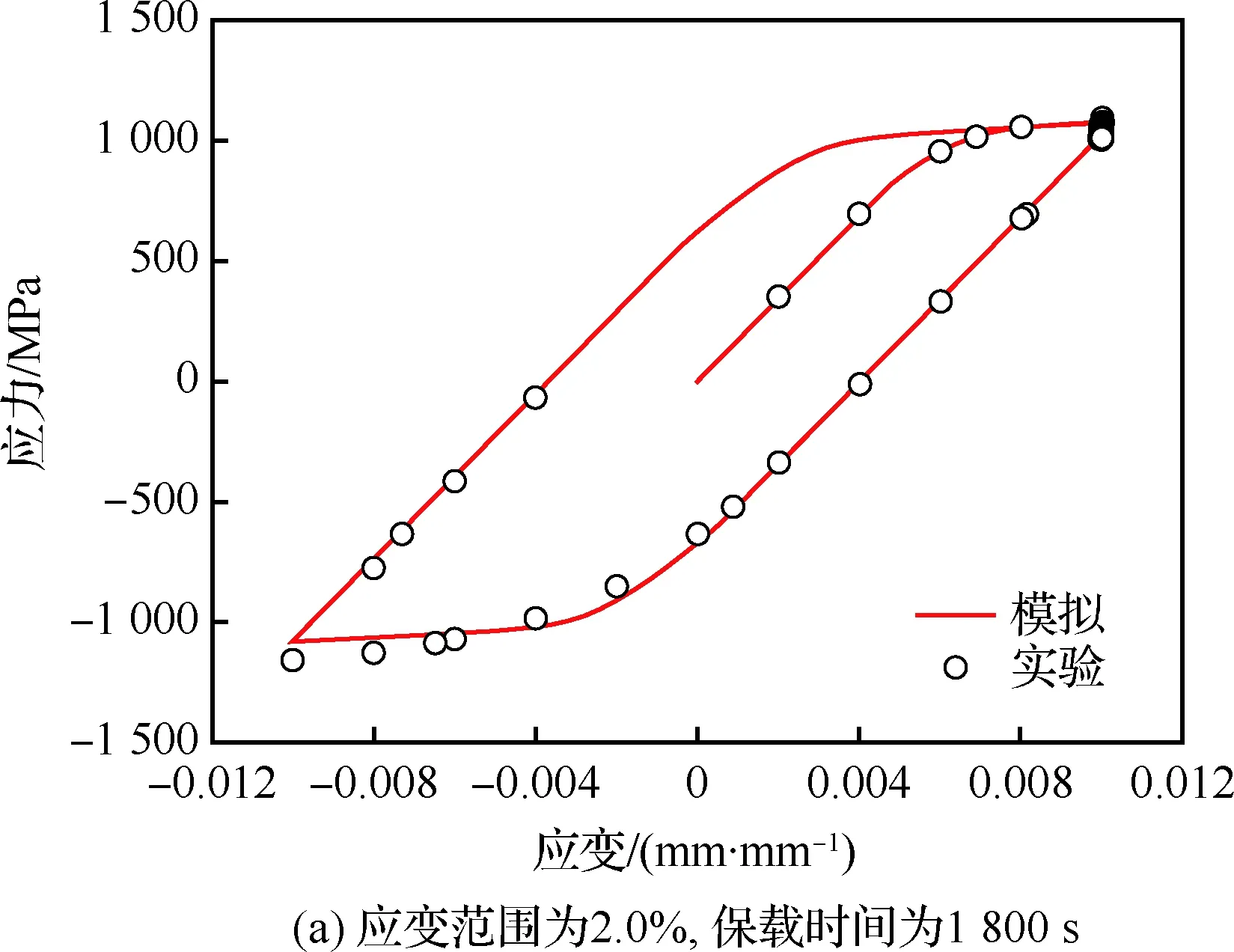
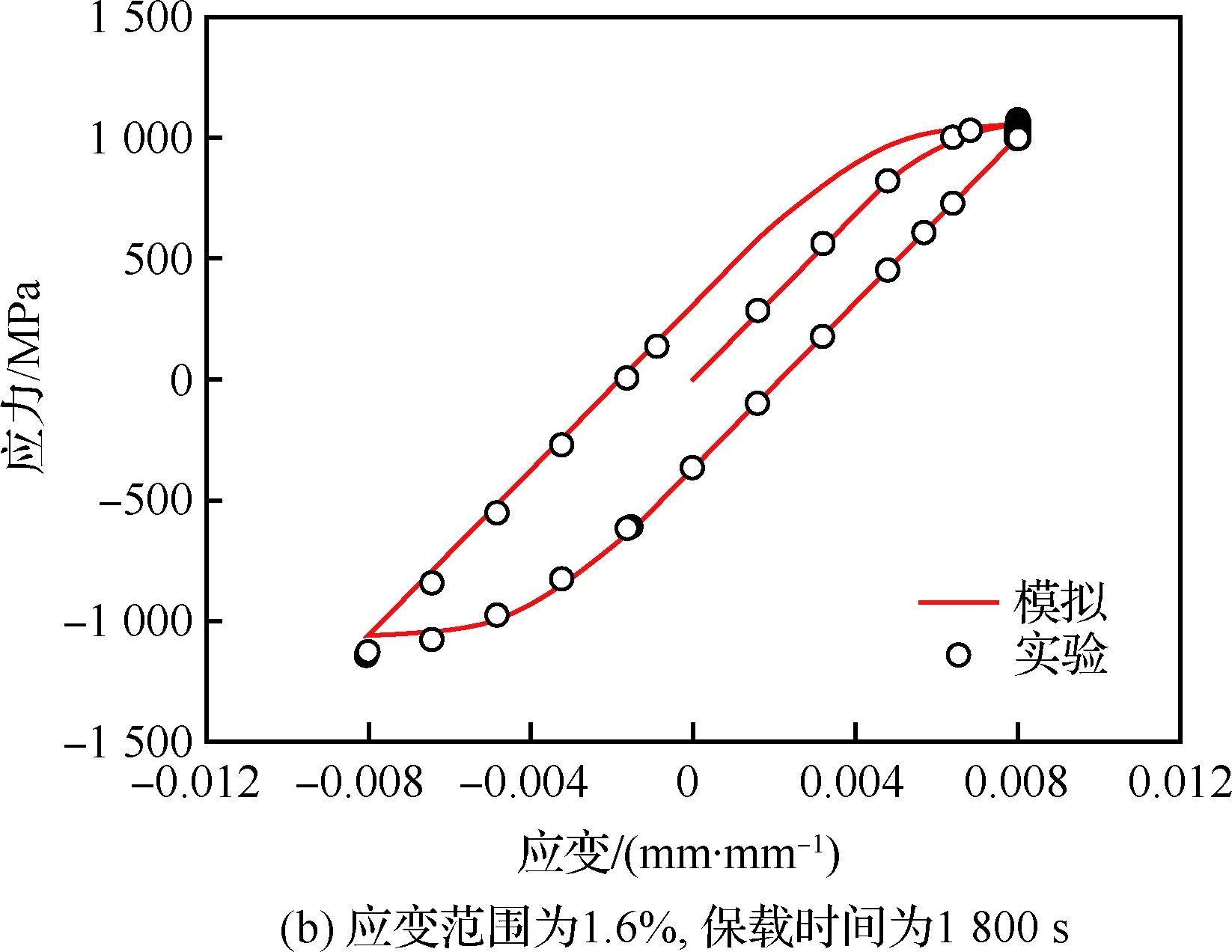
图7 不同应变水平和保载时间下的蠕变-疲劳滞回曲线Fig.7 Hysteresis loops for creep-fatigue at different strain levels and hold time

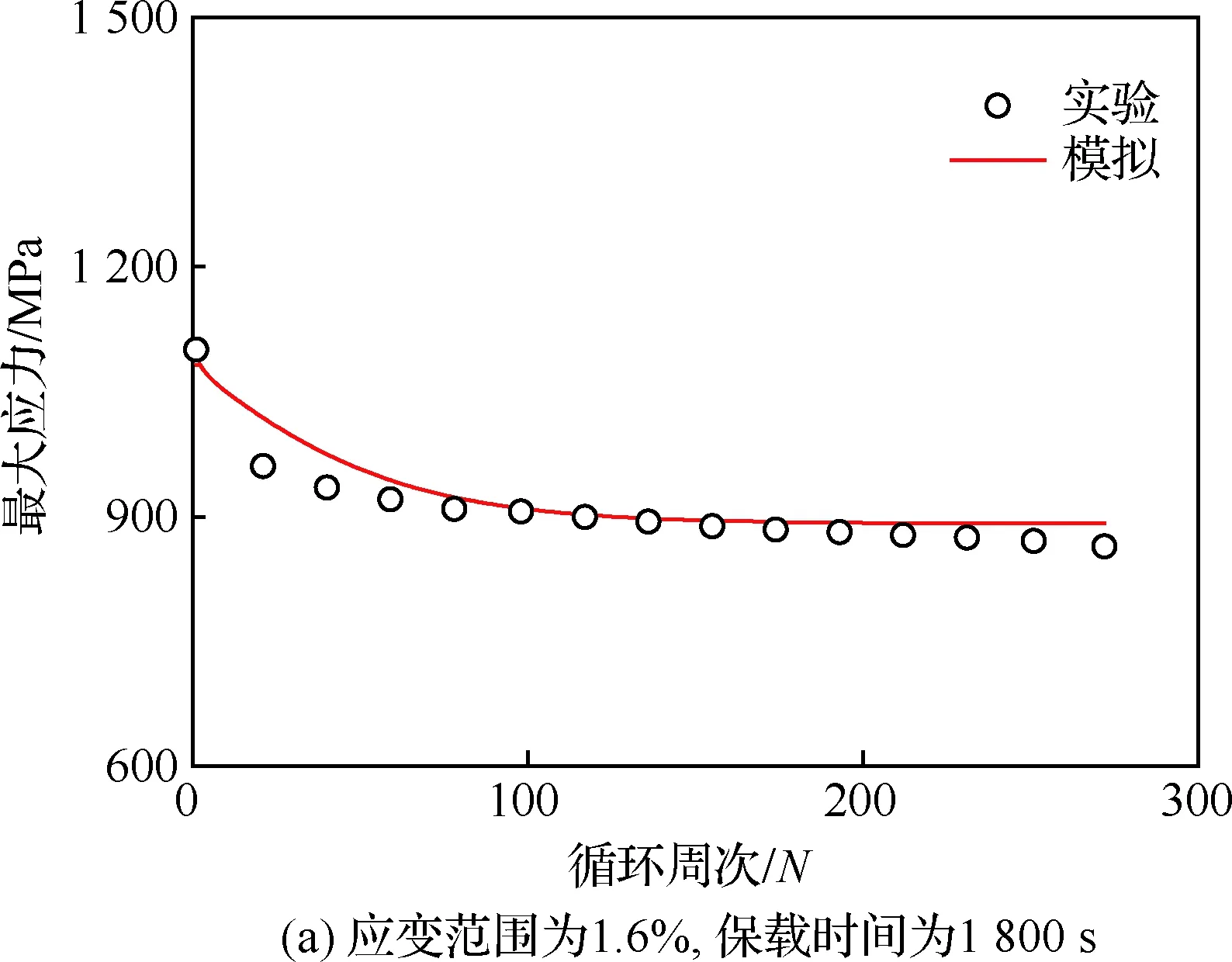
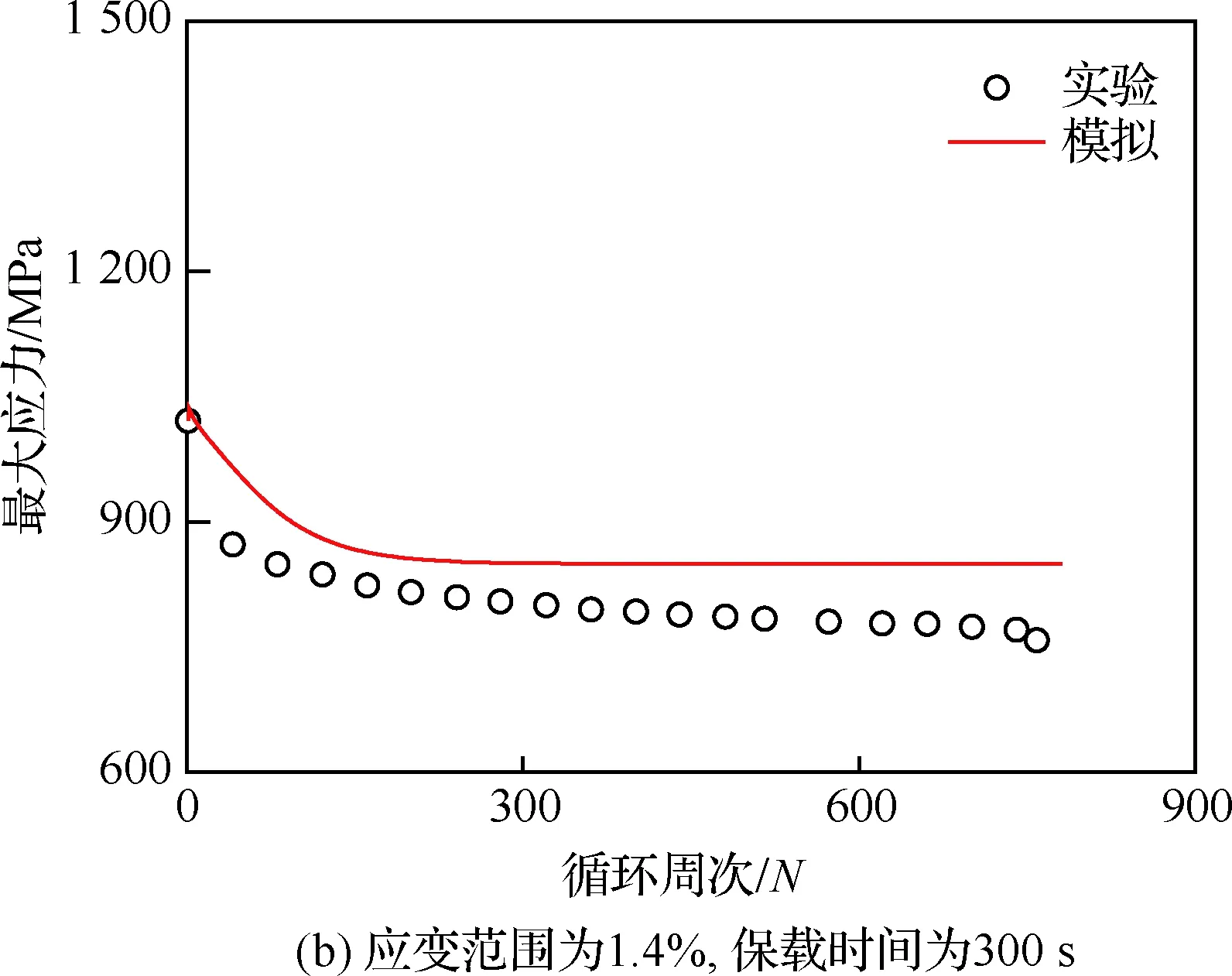
图8 不同应变水平和保载时间下的最大 应力-循环周次演化曲线Fig.8 Curves of evolution of the maximum stress with cycle number at different strain levels and hold time

3 GH4169合金蠕变-疲劳寿命预测及讨论

基于上述所需参数以及寿命预测过程，图9给出了基于ABAQUS模拟应变范围分别为2.0%、1.6%和1.4%，保载时间分别为1 800、300、120和60 s，应变比R=-1的蠕变-疲劳工况所得的GH4169合金的蠕变-疲劳寿命预测值与实验值[19]之间的对比结果。图中，两条平行的虚线表示±2倍的误差带范围。

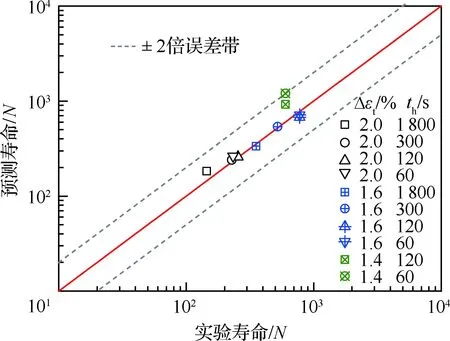
图9 蠕变-疲劳寿命预测值与实验值对比Fig.9 Comparison between creep-fatigue prediction life and experimental life

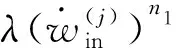
表1 基于逐周次概念的蠕变-疲劳寿命预测模型参数[19]Table 1 Parameters used in creep-fatigue life predictionmodel based on cycle-by-cycle concept[19]

4 结 论

1) 采用所选取的本构模型，结合合理的参数确定方法，可以精确描述GH4169合金在具有不同应变水平、不同保载时间的蠕变-疲劳载荷下循环第一周的应力-应变滞回环曲线，峰值保载阶段的应力松弛行为和最大应力-循环周次演化曲线。

2) 采用基于逐周次概念的应变能密度耗散的寿命预测模型，针对GH4169合金在不同载荷水平和保载时间下的蠕变-疲劳寿命得到了较好的预测，计算寿命均落在±2倍的误差带范围之内。

3) 采用的寿命预测方法，对载荷水平、保载时间等因素对GH4169合金蠕变-疲劳寿命的影响也得到了较好的描述和预测。