基于复杂网络的无人机飞行冲突解脱算法

黄洋，汤俊，老松杨

国防科技大学 系统工程学院，长沙 410000

近年来无人机系统被广泛运用到战争环境和城市环境中。由于执行任务环境和任务本身逐渐变得复杂，多无人机的集群作业变得越来越有研究价值。无人机之间能够实现自主防撞是无人机集群控制的前提，包括无人机群内部的防撞和无人机群之间的防撞，解决无人机群防撞问题对当前无人机集群作业具有重大意义。

无人机的动力学模型较为复杂，面临的威胁也有高度不确定性。因此在无人机遇到威胁时依赖飞控计算机进行路径生成，会影响无人机群执行任务的效率，同时也可能造成连锁碰撞[1]。考虑到无人机的集群防撞面临着空中威胁数量多、运动速度大等特点，通过对无人机群构建复杂网络，分析在受威胁状态下网络的性质以确定合适的避撞策略，使得无人机群在性能约束的条件下具备防撞能力，可大大提高无人机集群防撞的实时性、准确性和适用性。无人机避撞有很多算法，文献[2-3]对抽象的各种算法进行广泛和细致地调查并且总结了用于避免无人机之间碰撞的原型系统的概念。蒙特卡罗算法[4]在传统空中防撞系统(Traffic Collision Avoidance System，TCAS)算法上性能有所提升，但是主要解决一对无人机之间的防撞问题，没有考虑到全局空域的无人机状态。人工势场法[5]的优势在于应答时间很短、计算量小，因此具备实时性，但是通常不能准确到达目标而且产生的轨迹往往不适用于固定翼无人机，因此不能很好地解决大规模无人机防撞问题。蚁群算法[6]可以很好地解决多无人机的路径规划问题，但是考虑的防撞问题主要是固定的障碍物，在无人机集群防撞方面很难实现，并且需要大量迭代计算，所以不能满足无人机集群飞行时的防撞问题。遗传算法[7]也是仿生优化算法，与蚁群算法存在相似的问题，无法解决无人机群的实时防撞问题。共生模拟[8]本质上还是优化算法，优势在于产生的全局路径规划更加平滑，但是仍旧存在计算耗时长的特点，无法实时解决无人机群冲突解脱问题。几何优化算法[9]能解决无人机群的冲突解脱问题，但是由于仍然是优化问题，计算量比较大。概率算法[10]需要进行持续计算，很难满足实时性的需求。着色Petri网[11]主要应用在民航领域，主要考虑4架以下飞机之间的冲突，对大规模的集群运算无能为力。共识算法[12]解决了多个无人机交汇的问题，无人机对其将要到达交汇点的预计到达时间达成共识来解决冲突，但是也没能解决大规模条件下的无人机防撞问题。卡尔曼滤波算法[13]研究了射频信号在无人机位置估计和碰撞避免中的应用，提出了一种有色噪声模型，并将其应用于扩展卡尔曼滤波器中以进行距离估计，该算法解决了当全球定位系统不可用时的碰撞避免方案，但是没能对全局的无人机进行协调控制，局限于最后时刻的防撞。马尔科夫决策过程法[14]被创新地用于无人机追踪目标上，其防撞的策略是提前告知威胁无人机的实时位置，以此控制无人机在安全距离范围上。基于Dubins曲线算法[15]主要是通过判断不同路径的优劣来选择出避撞的路径，没有办法满足无人机群之间的防撞问题。预测控制算法[16]可以解决基本的一对无人机之间的防撞，并且文章是对直升无人机做的仿真实验。基于可达集的算法[17]对民航飞机防撞作了优化，可达集可以提升避撞的成功率，但是仍然无法解决无人机群的防撞问题。各种算法之间常常结合在一起使用。但这些算法主要是考虑成对无人机防撞，没考虑复杂多机态势下的集群防撞问题，同时存在迭代次数多、计算复杂、实时性不好等缺点，无法适用于无人机技术高速发展背景下的无人机集群防撞需求。当无人机数量增多时，需要适应于大规模的无人机防撞算法。文献[18-19]提供了多无人机情况下的冲突解脱方案，但都存在效率较低的问题。文献[20]设计了基于Skinner操作条件反射理论框架(GA-OCPA)的学习系统以达到对威胁的规避，这可以借鉴到多无人机条件下冲突解脱策略的算法中。

复杂网络理论认为关键节点有十分重要的性质[21-23]，对整个复杂网络系统的影响程度最大。本文提出的基于复杂网络的无人机避撞算法具有简洁、高效、实用等特点，最重要的是考虑了每一时刻无人机群系统的安全性指标使得整个飞行过程整体的安全性达到最大，这样的特性对于无人机群而言是非常有利的。该防撞系统由2个关键步骤组成：关键节点选择和避撞方向选择。本文算法将无人机群之间的威胁用复杂网络来表达，根据飞行速度、飞行角度、安全区域3个参数的变化建立无人机网络模型，通过网络的鲁棒性迅速减小来达到网络尽快溃散的目的，实现无人机群之间的威胁尽快消除。本文将全局空域分为很多小块，无人机分布在不同的子空间中。假设两群互相合作的无人机群朝着相反的方向飞行，在有实时通信的环境下所有的无人机朝着既定的目标进行飞行同时需要执行避撞操作。每一架无人机都配备有飞行轨迹控制单元，避撞系统计算出的避撞策略通过实时数据链接与周边的无人机进行信息交互。

1 模型构建

本节描述的是无人机集群的模型构建。首先，对冲突进行检测，定义了无人机的属性用以刻画无人机的各种状态，构建了无人机的邻域集以及冲突发生的条件。然后，说明了关键节点选择以及避撞方向选择策略，其中对一种意外入侵的特殊情况进行说明并提供解决方案。最后，对无人机的安全性定义了安全性分析指标。

1.1 冲突检测

将无人机用节点表示，无人机的状态被系统实时监控，其属性表示为{UAV, Velocity, Position, Angle,t, State, Sense, Strength, Approaching time, Time cost, Key node}。其中：UAV表示无人机编号；Velocity表示无人机速度；Position表示无人机当前位置；Angle表示无人机飞行角度；t表示无人机当前所处时刻；State表示无人机飞行状态(处于避撞路径上或原路径上)；Sense表示无人机避撞方向选择；Strength表示无人机方向改变程度；Approaching time表示无人机到达最近接近点(Closest Point of Approach, CPA)剩余的时间；Time cost表示在整个飞行过程中无人机消耗的时间；Key node表示无人机是否被选择为关键节点。

无人机有6种状态，分别是：状态1，正常的巡航状态；状态2，由防撞系统检测到刚好遇到威胁的状态；状态3，防撞系统检测到有威胁后开始执行避撞程序正在改变的轨迹上飞行的过程；状态4，在执行避撞的时间达到预计的位置时，按照原有巡航状态进行飞行的过程；状态5，在状态4结束后开始按照与防撞轨迹相反的角度进行返航回到原有轨道上；状态6，在返航过程结束后按照原有巡航的角度进行巡航。

为了检测冲突的目的，无人机在笛卡尔系统中被识别。每个无人机在相应时刻的位置表示为

(1)

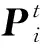
定义最大爬升(俯仰)角，该角度由无人机的性能决定，其限制了无人机在执行避撞任务时的航迹在垂直平面内的上升和下滑的最大角度，设最大俯仰角为φmax，约束可以表达为

(2)

对无人机进行邻域集的构建，无人机遇到威胁的坐标设为(x,y,z)，最小的邻域距离为lmin，最大的邻域距离为lmax，最低飞行高度为hmin，则无人机在飞行中的邻域点s的集合为

S(i)={s∈V-{i}|lmin≤d(i,s)≤lmax;

(3)

式中：d(i,s)为i和s之间在一个仿真步长的欧式距离；V-{i}为除无人机i当前位置之外的所有可能到达位置的集合。

定义最大偏航角为Φmax，其到达目标的后向邻域为A(i)，预计的到达角度为θgoal。

A(i)={s∈V∧s≠g|lmin≤d(i,g)≤lmax;

(4)

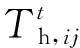
(5)

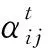
(6)

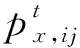
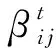
(7)

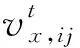
(8)

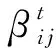
(9)

这表示左右两个条件只要一个被满足，TA事件即被触发。用T1来表示第1对无人机触发TA警报的时刻。从那一刻起，构建一个网络，每个无人机都被表示为一个节点。如果一对节点发生冲突，则节点将建立连接。在时刻T1，系统中的所有节点将检查无人机是否正在接近，如果无人机正在彼此接近，则连接两个节点，判断条件为

(10)

这表示左右两个条件只要一个被满足就代表2个节点在相互靠近。在一对无人机情况下，按照以下原则进行避撞。无人机防撞示意图如图1所示，UAV1从右侧至左侧进行巡航，UAV2和UAV3从左侧向右侧进行巡航，此时UAV1被选择为关键节点，可以根据此时的场景进行避撞方向选择，其中向上爬升和向下爬升预计CPA时刻的目标点与UAV2和UAV3需保持最小安全距离ALIM(Altitude LIMitation)。具体的关键节点选择和方向选择策略由后文论述。

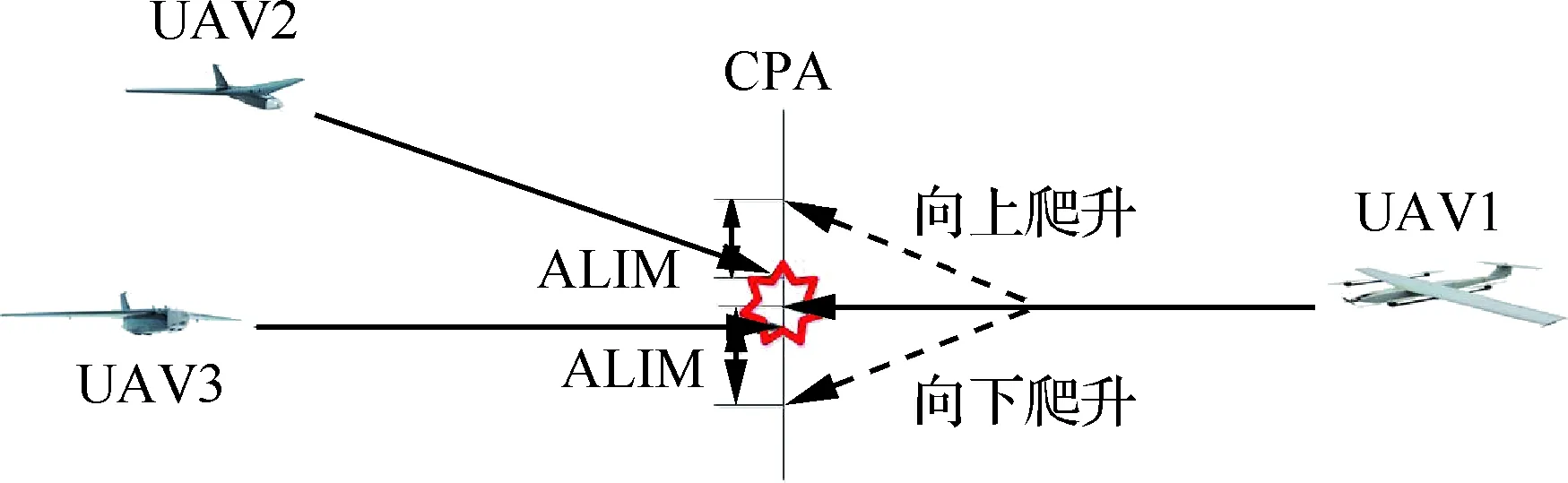
图1 无人机防撞示意图Fig.1 Sketch of collision avoidance of UAVs

1.2 关键节点选择策略

定义碰撞空间，在系统检测到一对无人机有碰撞风险时，系统通过全域数据分析得到所有的未来可能撞击的无人机编号并获取对应无人机的状态。由这些无人机组成的空域被称作碰撞空间。其中对有碰撞风险的无人机之间进行连线，形成网络进行分析。用邻接矩阵记录无人机之间的状态。用节点N代表无人机，用边E代表无人机之间的关系。定义一个集合Ω以包含满足条件的节点。本文以2组无人机在2个不同的垂直平面上的情景为例阐述概念。如图2所示，2组节点分布在相应的垂直平面上。图中：红色节点和蓝色节点表示两组相向而飞的无人机；节点之间的连线表示节点之间存在威胁关系；1 n mile=1 852 m，1 ft=0.304 8 m。网络建成后，制定网络描述规则来描述多无人机系统的内部特征。网络中的节点在不同的无人机群中具有不同的属性。

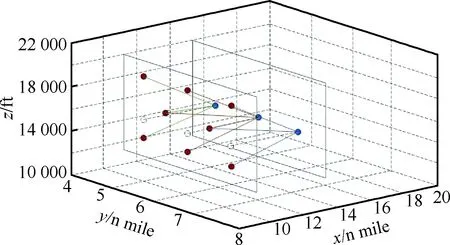
图2 无人机群复杂网络概念图Fig.2 Conceptual framework of complex network for UAVs

为了使网络更加接近于真实场景，只使用边数是不够的。边应该有额外的属性来监视无人机的真实关系。该关系包含无人机之间的相对距离和相对速度。一对无人机接近对方的速度越快，就越危险。所以每条边的权重取决于无人机之间的相对距离和相对速度，从而定义无人机i与无人机j之间的边缘权重ωij为

(11)

式中：υij为矢量方向的相对速度；dij为无人机i和无人机j之间的距离。这就意味着2架无人机接近的速度越快，无人机之间的边的权重就越大。关键节点选择的公式为

(12)

计算每架无人机的边缘权重之和，边缘权重之和最大的节点被定义为关键节点。即选出使得边缘权重之和最大的无人机序号ikey。

1.3 避撞方向选择策略

在这个新冲突模型情况下，尽可能地降低鲁棒性和完整性至关重要。将网络的鲁棒性定义为

(13)

(14)

式中：I为网络中被剔除的节点数量；M为网络子图中最大的链接数量。

这个新模型的目标是尽可能快地分解网络。这意味着在关键节点被清除之后，网络的鲁棒性和网络的组件数量应该尽可能低。也意味着无人机相互离开，坠毁的风险越来越小。在仿真步骤中，新模型找出关键节点并评估连接的鲁棒性或连接的组件数目。关键节点将选择变化的航向，在下一个仿真步骤中形成一个新的网络，新的模型将再次选择关键节点。该模型将监测多无人机系统，以确定是否发布TA警报，如果模型停止查找关键节点，多无人机系统将被认为是安全的。

如图3所示，该场景描述的是在一个特殊的垂直面碰撞空间内的无人机关联情况。每个节点代表不同的无人机，红色节点和蓝色节点分别表示2个飞行朝向的无人机群，虚线框表示系统认为的蓝色节点受威胁区域，在受威胁区域内的红色节点被认为是对蓝色节点产生威胁的节点。由于在该场景下，红色节点的受威胁区域内包含的蓝色节点数最多为2个，而蓝色节点的受威胁区域内包含的红色节点个数都至少是2个，因此在该场景下，按照图示顺序先后由中间的蓝色节点、左侧蓝色节点、右侧蓝色节点作为关键节点，由鲁棒性最小原则可得这些节点的避撞方向均为下降的方向。

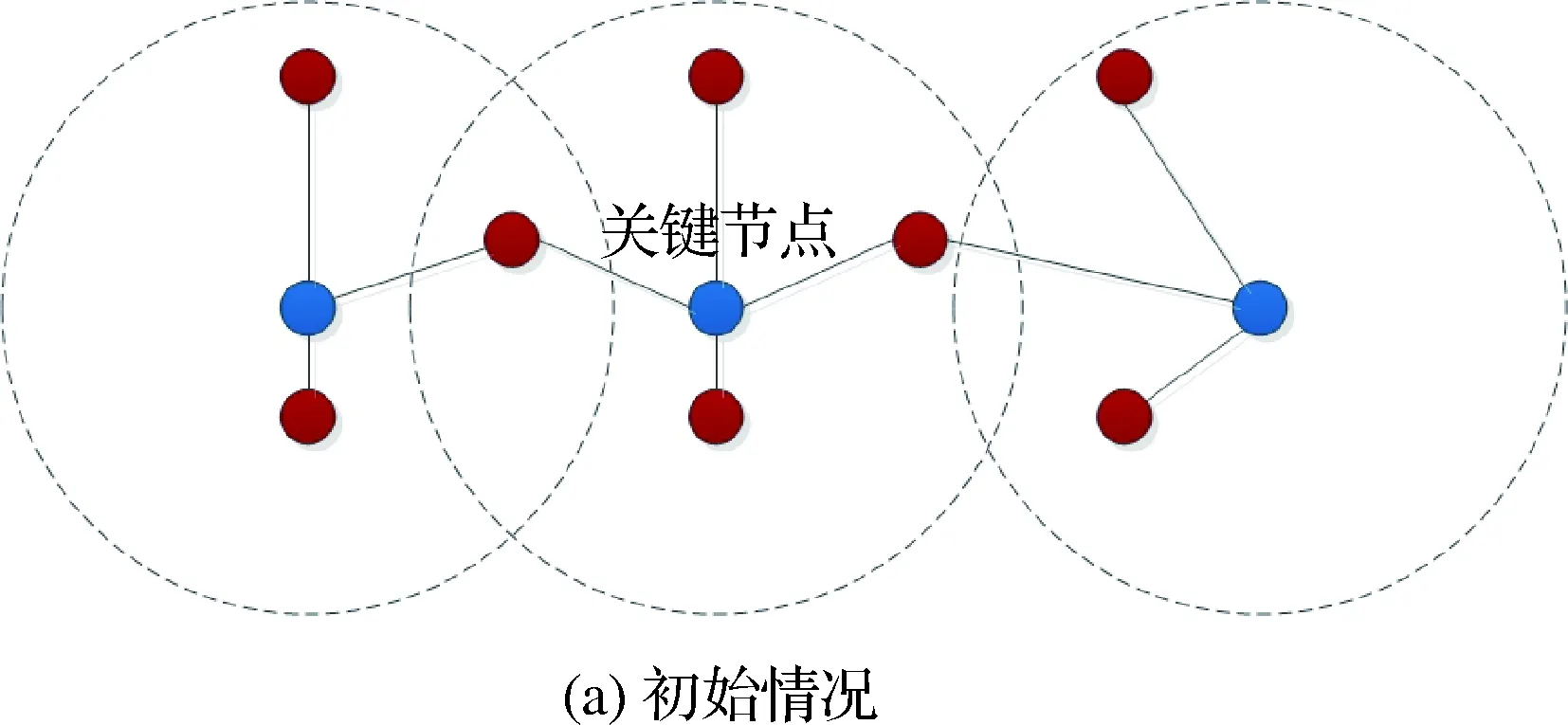
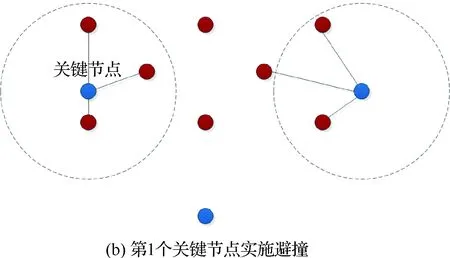
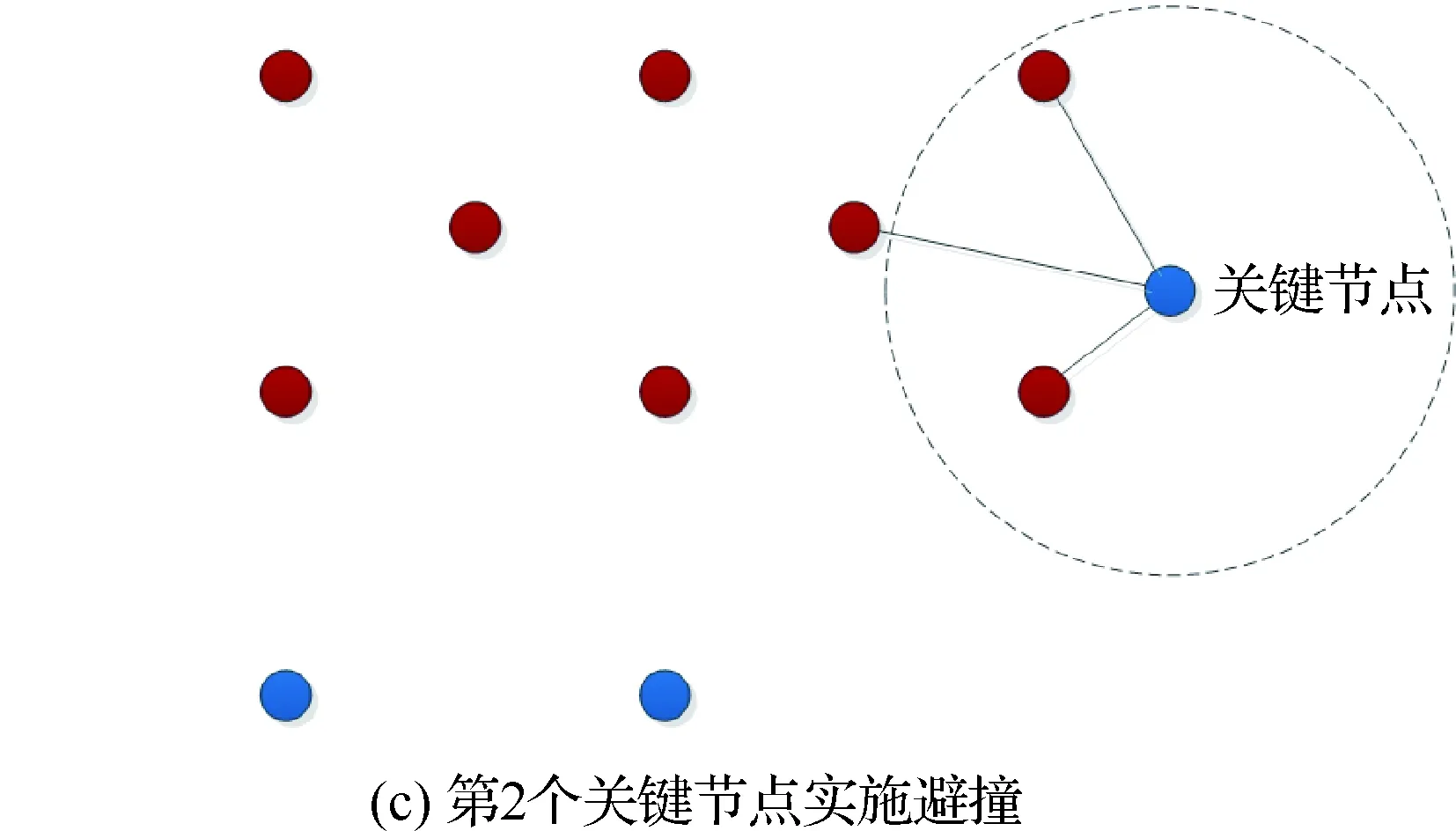
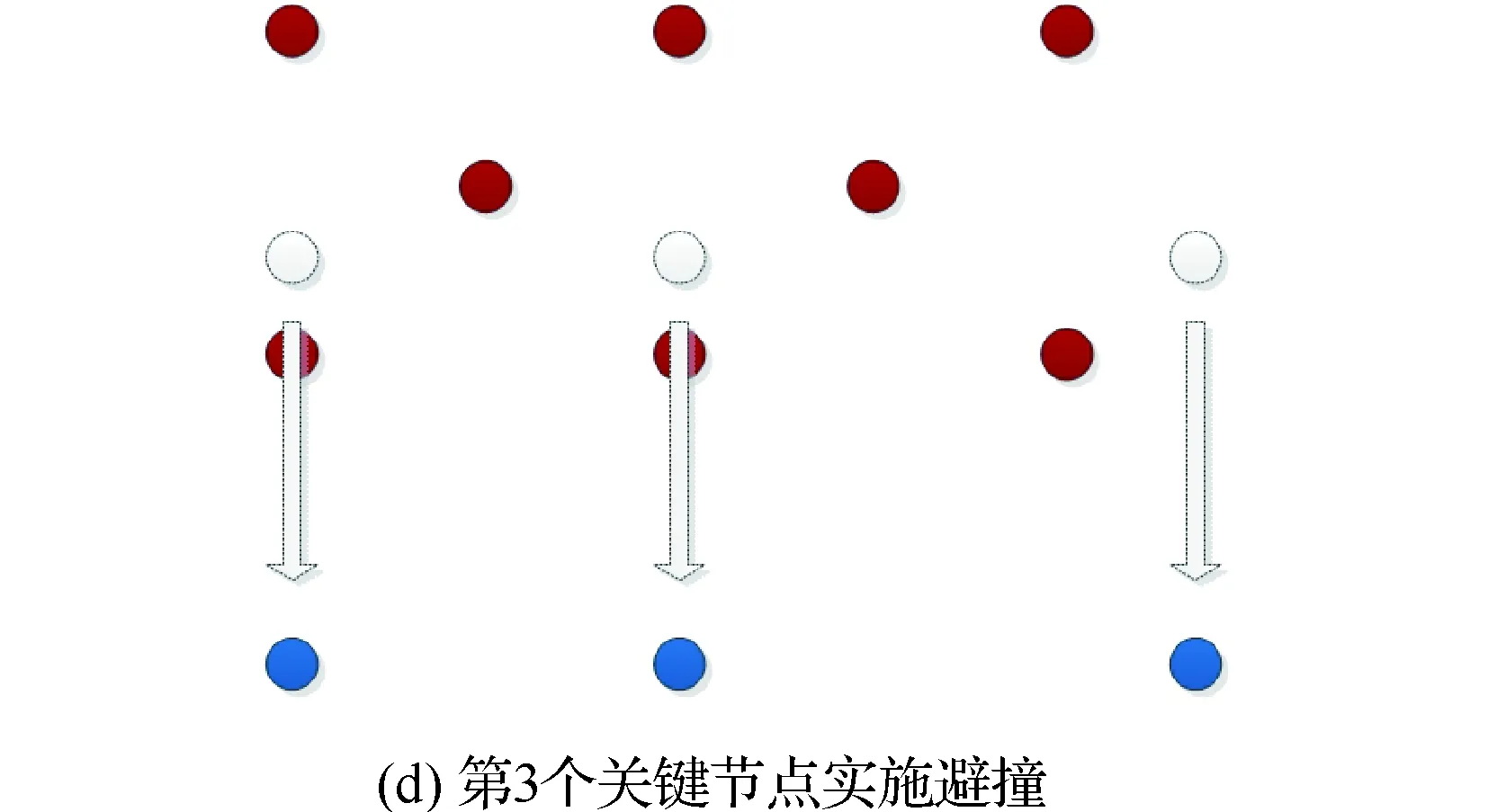
图3 查找关键节点的过程示意图Fig.3 Sketch of process of locating key nodes

由于无人机群防撞仍然不可避免地依赖基于一对无人机的冲突解脱过程，同时也需要考虑特殊情况，即在空域的边界处如果出现新的入侵无人机可能会发生新的碰撞，因此构造相应模型解决这种特殊情况。假设首次触发RA(Resolution Advisory)的时刻为t，并且关键节点对应的无人机和相应的入侵无人机m遵从同样的避撞逻辑。在时刻t+Δt出现新的入侵无人机m，在这种情况下关键节点对应的飞机没有改变其飞行轨迹，方向改变的规则将遵循优先级规则，此时能够提供最大竖直方向分离距离的方案将被选择，这与在既定空域内的避撞方向选择的原则一致，即保证在威胁时刻安全性达到最大。

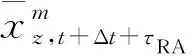
当选择向上飞时：

(15)

当其方向不做改变时：

(16)

当选择向下飞时：

(17)

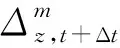
在最近接近点处关键节点对应的无人机与入侵无人机m的竖直距离表示为

(18)

(19)

(20)

当关键节点对应的无人机在完成自己的方向计算之前就接收到入侵无人机m的方向选择建议或者无人机i的优先级比入侵无人机m低，则无人机的方向选择按照如下公式进行：

(21)

入侵无人机的RA方向选择满足

(22)

(23)

式中：

(24)

1.4 无人机的安全性分析

文献[24]对冲突解脱的结果进行了安全性验证。在本文中考虑某个时刻的无人机群的安全性，提出基于状态的安全性指标。按照Q统计的方法可以对无人机群进行安全性分析。

(25)

式中：Xi表示第i架无人机撞毁的可能性，这里就用第i架无人机的鲁棒性指标Ri表示Xi；N代表无人机群的无人机数目。由于Q衡量的是某个时刻的安全性，因此每一架无人机的安全率的提高能够提高无人机群的安全性。

2 关键步骤分析

本节描述的是无人机集群防撞的算法，本文将该算法分为步骤1和步骤2，分别对应关键节点选择步骤和避撞方向选择步骤。2个步骤也分别对应无人机防撞过程的2个阶段，即防撞系统选取避撞的无人机序号和该无人机避撞的方向。

2.1 关键节点选择步骤

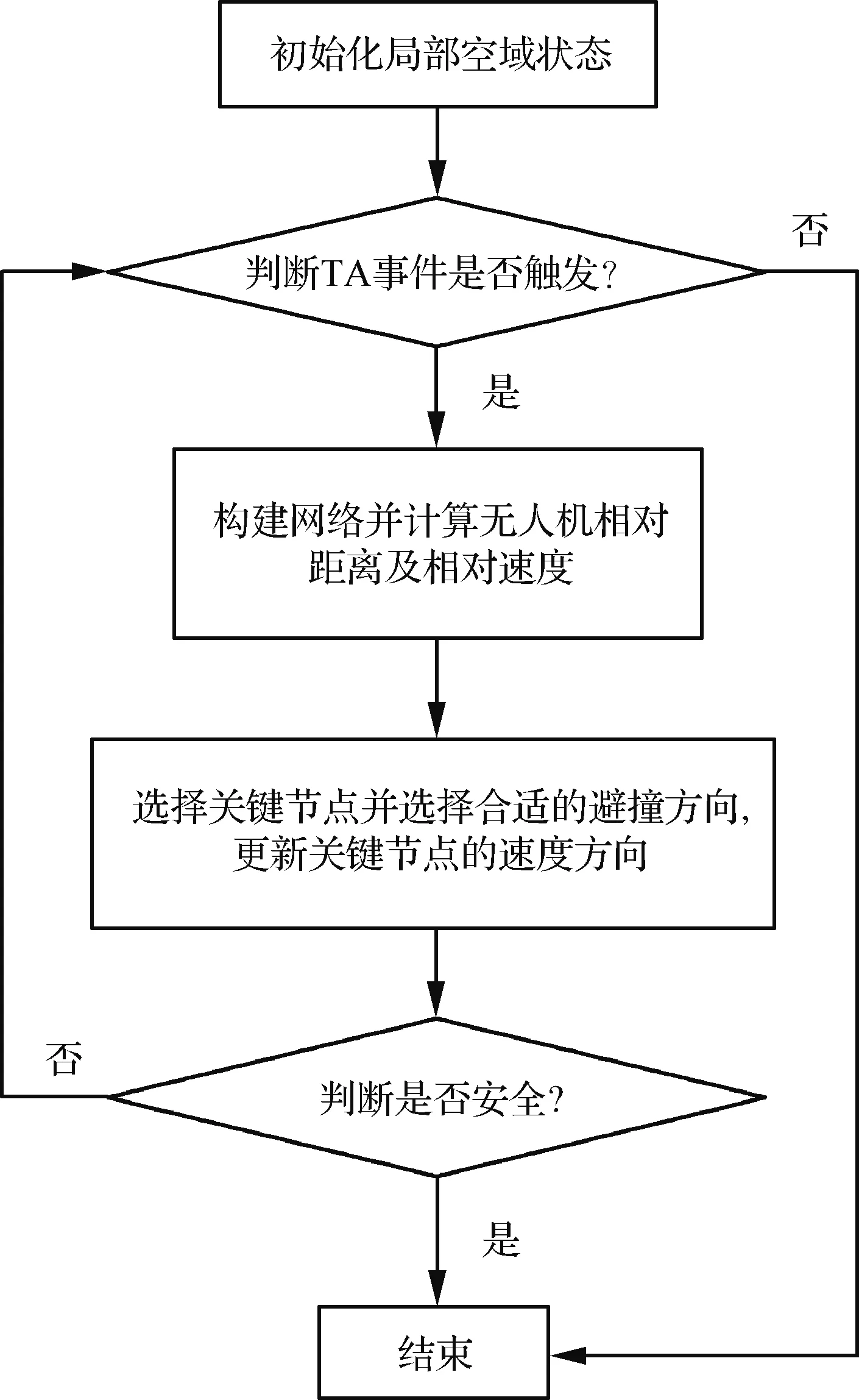
图4 关键节点选择步骤流程图Fig.4 Flowchart step for key node selection

关键节点选择步骤解决了避撞策略的第1步，即选择关键节点并由关键节点对应的无人机继续执行方向选择步骤提供的方向策略。关键节点选择流程图如图4所示，对仿真整个过程和每一架无人机进行检测是否有TA事件触发，一旦有TA事件触发，对无人机群进行网络构建，计算被包含无人机之间的相对速度和相对距离，然后通过计算受威胁程度值选择出关键节点并执行步骤2，在为关键节点选择好避撞方向后，更新关键节点的状态。步骤1不断执行，TA事件消除时进入下一个循环，更新全局无人机的状态。如果所有无人机到达安全区域，则步骤1终止。

2.2 避撞方向选择步骤

步骤2是对无人机避撞方向选取策略的描述，当防撞系统执行到步骤2中，如图5所示，首先会为关键节点构建探测网络从而对关键节点所处状态进行分析。由于组建探测网络时是对一定范围内的空域进行探测，所以分为单机入侵和多机入侵2种场景。如果探测网络中关键节点的入侵机数为一架，若探测与关键节点的垂直高度差小于1/(2ALIM)，构建全局分析网络,分别计算关键节点选择上升和下降的全局鲁棒性并选择鲁棒性小的方向；若入侵机与关键节点的垂直高度差大于1/(2ALIM)，则直接选择垂直方向上远离入侵机的方向进行避撞。如果探测到多机入侵，则考察入侵机群中与关键节点对应无人机垂直方向高度的相对高度，若更多的无人机高于关键节点的高度，则关键节点选择向下的方向进行避撞；若低于关键节点的入侵无人机数量更多，则关键节点选择向上的方向进行避撞。

3 仿真实验及结果分析

在本节中仿真计算出的结果能够展示出在动态情况下的多无人机防撞操作效果。本文设置了了仿真场景1和场景2，分别对应复杂多机垂直平面相遇场景和复杂多机无规则集群场景。初始化参数如表1所示。其中：A和B指的是无人机避撞过程中俯仰角度改变的范围区间。仿真步长设为1 s，即每1 s都会对全局空域的威胁进行分析并给出解决方案，系统也会实时更新无人机的飞行状态。在后文的仿真中，如果遇到无人机群数量庞大的场景时，会对空域做均匀的划分，然后每个仿真步长及时更新全局空域的无人机状态，这样相当于直接对全局无人机计算进行的一个简化，以此提升计算效率。例如50架飞机的情况下，由于两两无人机间需要进行计算，这样就要进行50×50次的威胁判断，但是分成5个空域后(此时每个空域有10架无人机)就只需进行10×10×5次威胁判断，大大减少了威胁判断次数，从而提升计算效率。

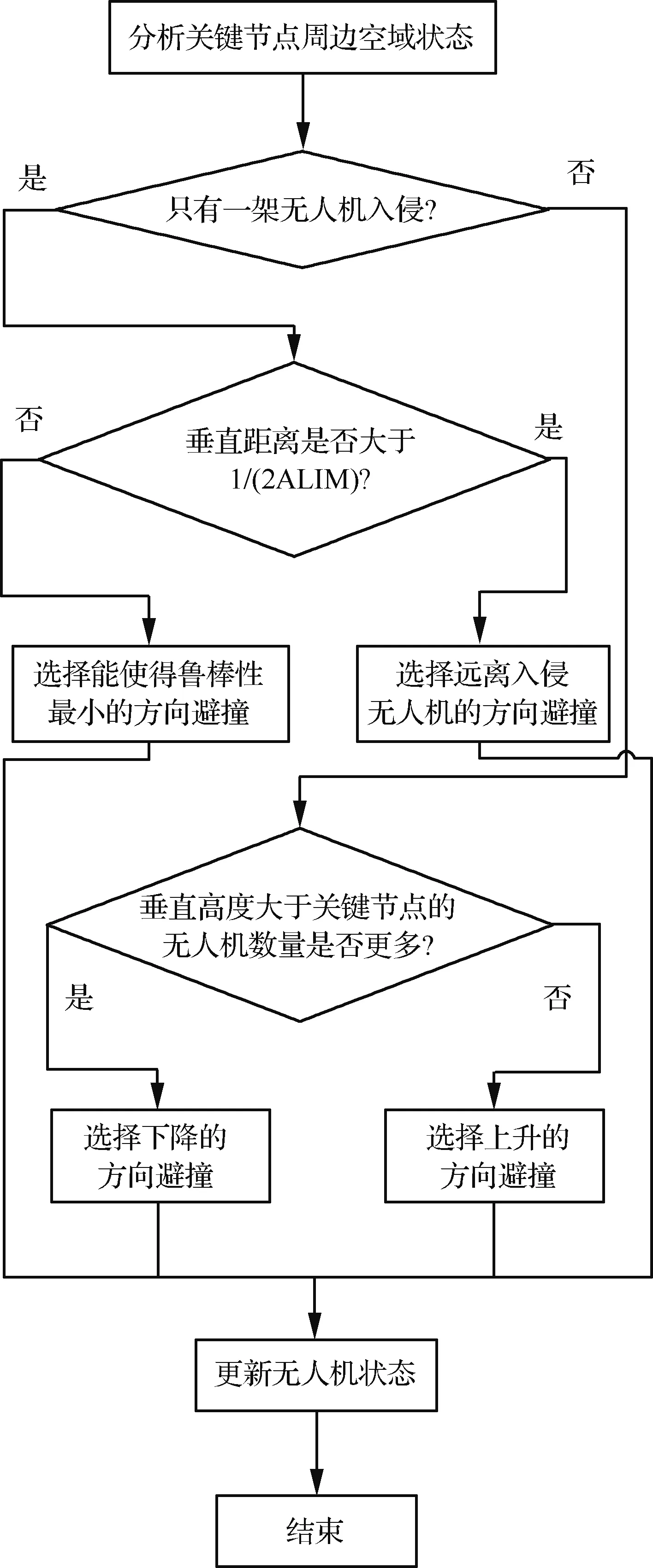
图5 避撞方向选择步骤流程图Fig.5 Flowchart step for sense selection

表1 无人机的假设参数Table 1 Hypothetical parameters of UAVs

参数探测距离/km预警范围/m速度/(m·s-1)Δt/sA/radB/rad数值1.2100301-0.6120.612

3.1 复杂多机垂直平面相遇场景

在本场景中，UAV1与UAV6有相撞威胁，UAV2与UAV7有相撞威胁，UAV3与UAV8有相撞威胁。按照本文提出的避撞策略，UAV1、UAV7、UAV8先后成为关键节点，避撞的方向选择与鲁棒性最小原则相一致，整个避撞过程如图6 所示，其中Tr1～Tr9分别代表UAV1～UAV9的飞行轨迹。在第1次的冲突中，UAV1与UAV6触发了TA事件，在该时刻防撞系统检测到UAV1面临的威胁有2个，分别是UAV6和UAV9，UAV6只有1个威胁UAV1，因此此时选择UAV1作为关键节点进行避撞处理，再按照鲁棒性最小原则选择下降方向进行避撞。第2次冲突的无人机对为UAV2与UAV7，此时UAV7面临3个威胁，分别是UAV7、UAV4、UAV5，而UAV2只有UAV7一个威胁，因此选择UAV7作为关键节点，该场景下无人机下降的方向符合鲁棒性最小原则的方向，此时可以保证整体状态安全性最高。同理在第3次冲突中，UAV3和UAV8触发了TA事件，UAV8面临的威胁为UAV3和UAV5，威胁个数为2，而UAV3只有UAV8威胁，因此选择UAV8作为关键节点进行避撞，并且选择上升的方向能保证鲁棒性最小。

图7描述的是在每一对存在冲突的无人机之间的相对距离，图中展现的是UAV2与UAV7，UAV3与UAV8，UAV1与UAV6之间的相对距离(分别用d27、d38和d16表示)随时间的变化情况。从图7中可以发现在整个避撞过程中，无人机之间的最小垂直面相对距离为39.24 m，满足无人机的安全距离限制。由于算法中实施的是单机改变方向的形式，在无人机未达到预设避撞高度时，无人机相对距离会略有缩小，但是能保证一定不会相撞，因为在预计的碰撞时刻无人机已经飞行至安全高度，所以虽然在避撞过程中可能会有接近的趋势，但在随后的飞行路径中无人机能够保持相对安全的相对距离。

图8描述的是在避撞过程中的网络连接，连线表示无人机之间存在的潜在威胁，其中连线的方式与构建网络的逻辑相同，节点之间存在关联不仅和节点之间的相对距离有关，同时与节点之间的相对速度有关。通过网络算法可以识别关键节点，然后根据网络属性选择最合适的避撞方向。

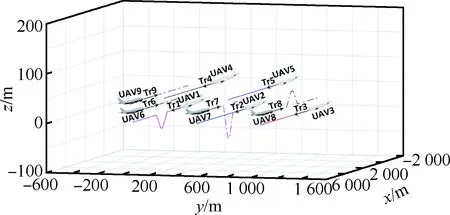
图6 无人机群垂直平面避撞场景Fig.6 Scenario of UAV collision avoidance on vertical plane

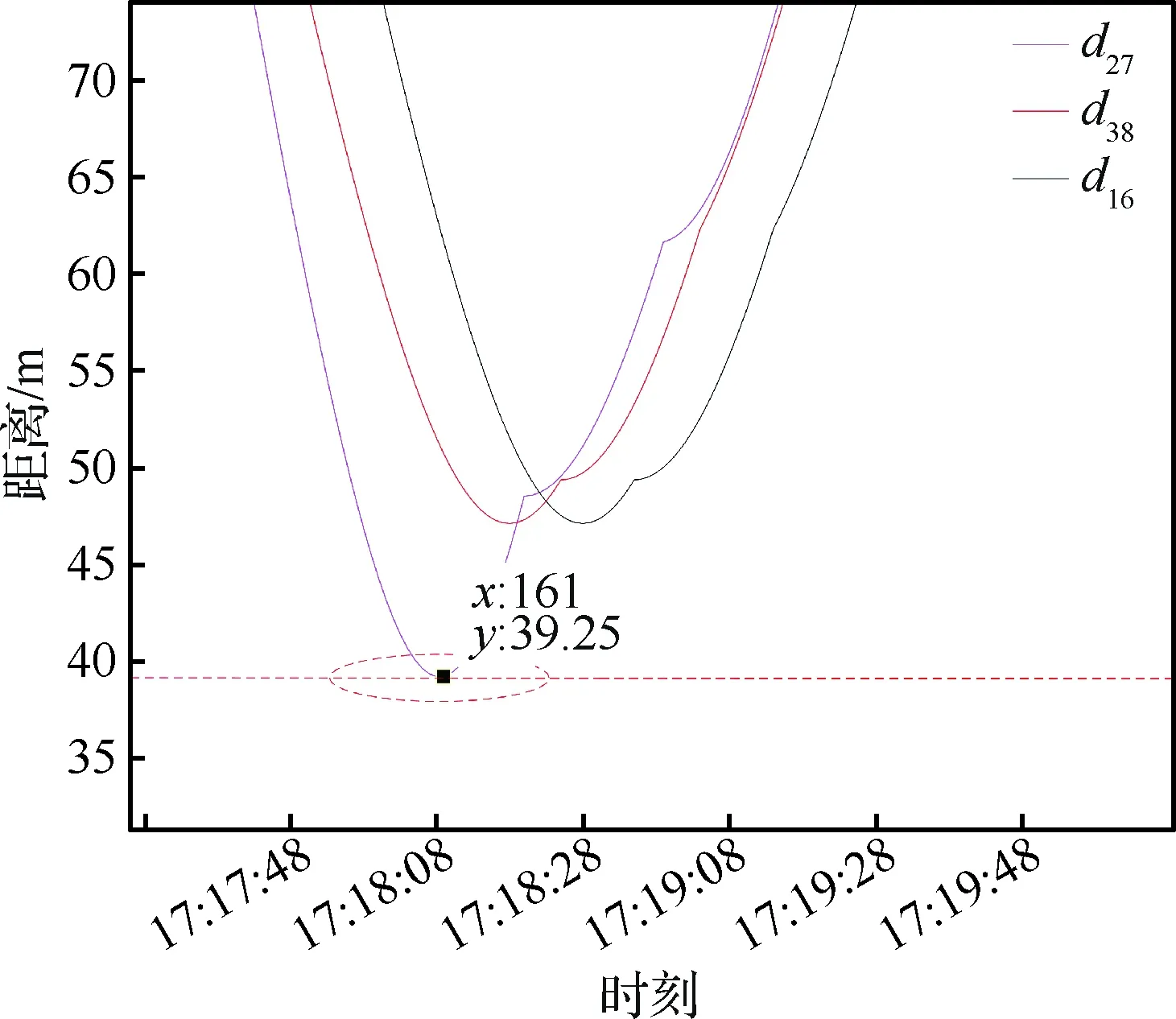
图7 场景1下无人机之间的相对距离Fig.7 Relevant distance of UAVs in scenario 1

图8 场景1避撞过程中的网络连接Fig.8 Network of collision process in scenario 1

3.2 复杂多机无规则集群场景

为了检验本文提出算法的可行性，进行仿真实验得到考虑了包含9架无人机的人为设计的场景下,由该算法自动产生的避撞效果，如图9所示。这个场景具备3个特点：① 场景相对复杂；② 多米诺效应；③ 同时考虑到了短时间内多次威胁的情况。

解决的策略就是通过分析在场景内各无人机的被威胁程度选择执行避撞过程的无人机，然后再根据鲁棒性最小原则选择避撞的方向。

在该场景中，每一架无人机都在以直线的方式按初始方向进行巡航。在仿真的初始化阶段为每一架无人机的初始位置和初始速度赋值。在有撞击危险的区域，无人机利用本文提出的算法对该场景生成解决方案进行避撞。在局部空间内，无人机通过广播的形式告知防撞系统实时的空域状态，所有无人机的信息都能通过实时有效的通信设施进行状态的记录与更新，通过避撞系统为所有的无人机给出避撞方案。

表2总结了该场景下的无人机初始位置和飞行角度。在本场景中，第1次出现的TA是UAV1和UAV4触发的。经过避撞系统分析后发现UAV1除了与UAV4即将发生碰撞外，还有潜在的和UAV2发生碰撞的可能，因此第1次发生TA事件时系统选择了UAV1作为关键节点进行避撞方向的选择，此时UAV1选择了向下进行避撞。随着仿真步长推进，系统检测到在下一个阶段在上UAV1与UAV2触发了TA事件，由于UAV1已经在上一个阶段成为了关键节点，因此在本次冲突中UAV2的潜在威胁虽然只有UAV2与UAV1之间的冲突，但是由于UAV1已经成为了一次关键节点，在这种情况下UAV2被系统选为关键节点，并为其分配了向上避撞的策略，这样使得在原本将要撞击的时刻，系统纠正了无人机航线后使得引起冲突的这几架无人机形成分散规避撞击的态势，这可以解释在这时该区域内的网络鲁棒性实现了最小化，直观映像就是3架无人机散开了而并没有出现交叉航线等会造成多米诺效应的后果。

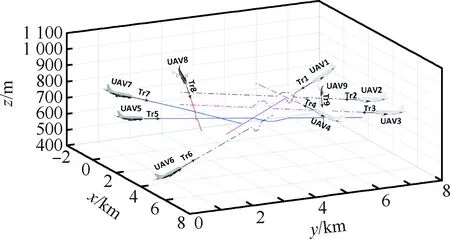
图9 无人机群随机位置避撞场景Fig.9 Scenario of UAV collision avoidance at arbitrary locations

表2 无人机群的初始状态Table 2 Original states of UAVs

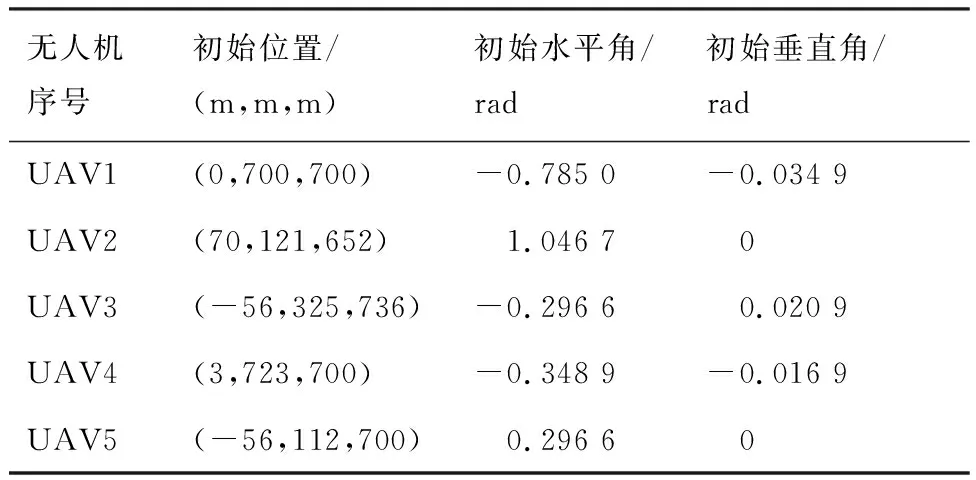
无人机序号初始位置/(m,m,m)初始水平角/rad初始垂直角/radUAV1(0,700,700)-0.785 0-0.034 9UAV2(70,121,652)0.1.046 70.0UAV3(-56,325,736)-0.296 60.0.020 9UAV4(3,723,700)-0.348 9-0.016 9UAV5(-56,112,700)0.0.296 60.0

第3个出现连续TA事件触发情况的是UAV1、UAV3和UAV5之间。下一个TA事件触发是由UAV1和UAV3引起的，同理在这种情况下UAV3遇到的威胁和UAV1一样多，但是UAV3之前不是关键节点，因此在这一次的关键节点选择中UAV3成为了关键节点，并被系统分配了向上避撞的策略。紧接着UAV5检测到即将与UAV1发生撞击，而此时UAV1正处于避撞过程中，关键节点选择优先级不如UAV5高，系统同时检测到此时在UAV5未来的上空有正在执行避撞过程的UAV3，因此此时UAV5选择向上避撞的优先级不如向下避撞的方向选择优先级高，所以此时UAV5选择了向下避撞的策略。这一次的连续TA事件触发的情况和第1次有所不同，同时涉及到了关键节点的选择时间，成为关键节点之后的节点在下一次评价是否成为关键节点时优先级会降低。

由于在算法的设计阶段已经考虑到了连续TA事件触发的情况，因此按照既定的关键节点选择原则和避撞方向选择原则能够在这种连续TA事件触发的情况下由防撞系统综合分析态势为每一架无人机分配有利于空域全局发展的安全性 较强的避撞策略。表3总结了UAV1和UAV2的路径。

图10描述的是在每一对存在冲突的无人机对的相对距离，图中展现的分别是UAV1与UAV4、UAV1与UAV3、UAV1与UAV2、UAV1与UAV5之间的相对距离(分别用d14、d13、d12、d15表示)随时间的变化。从该图中可以发现在整个避撞过程中，无人机之间的最小相对距离为35.86 m，满足无人机的安全距离限制。由于算法中实施的是单机改变方向的形式，在飞机未达到预设避撞高度时，无人机相对高度会在一小段区间内小于ALIM，所以虽然在避撞过程中可能会有接近的趋势，在随后的飞行路径中无人机能够保持相对安全的相对距离。

表3 UAV1和UAV2的路径Table 3 Route of UAV1 and UAV2

图11描述的是场景2避撞过程中的网络连接，与图8相同，网络展现的拓扑形态描述了该场景此时的无人机之间的受威胁情况。

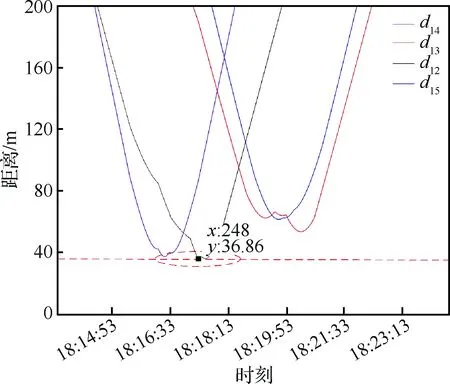
图10 场景2下无人机之间的相对距离Fig.10 Relevant distance of UAVs in scenario 2

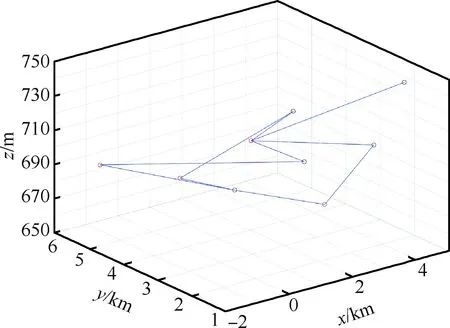
图11 场景2避撞过程中的网络连接Fig.11 Network of collision process in scenario 2

3.3 结果分析

由于在算法的设计阶段已经考虑到了连续TA事件触发的情况，因此按照既定的关键节点选择原则和避撞方向选择原则能够在这种连续TA事件触发的情况下由防撞系统综合分析态势，为每一架无人机分配有利于空域全局发展的安全性较强的避撞策略。

为了比较本文提出算法的优越性，将基于复杂网络避撞算法和随机选择方向避撞算法做比较，表4对比了使用基于复杂网络的避撞算法和随机选择方向避撞算法的Q值，也就是探测到威胁的原撞击时刻的安全性。表4中展示了不同空域无人机密集度情况下(18架、32架、50架、72架、 100架)的Q值结果，其中Q值为30次仿真实验结果的平均值。在不同的无人机密度的情况下基于复杂网络避撞算法的Q值始终比随机选择方向避撞算法要小，意味着基于复杂网络避撞算法能够使得在探测到威胁的原撞击时刻的空域无人机群的安全性可以达到最大。同时随着密度的增加效果并没有明显减退，表明算法本身的稳定性很好，适用于大规模无人机群的避撞。

表5为复杂网络算法与其他算法的计算效率比较。为了验证算法的可适用性，本文用计算时间消耗作为衡量本防撞算法在不同无人机密度下的效果，并将其与其他算法进行比较，用2个经典的被验证对于高密度环境有效的SGTA(Satisficing Game Theory-based Algorithm)和RIPNA(Reactive Inverse PN Algorithm)作为比较。如表5所示，低密度(20架无人机)、中密度(40架无人机)以及高密度(60架无人机)条件下的平均计算时间(基于100次随机场景仿真测试)随着空域无人机密度的增加不会呈现指数增长的形式，并且在不同密度下计算效率与其他算法相比有显著提升。算法的可适用性是可以保障的，因为即使在高密度无人机场景下仍然能在相对合理的时间范围内计算出冲突解决方案。

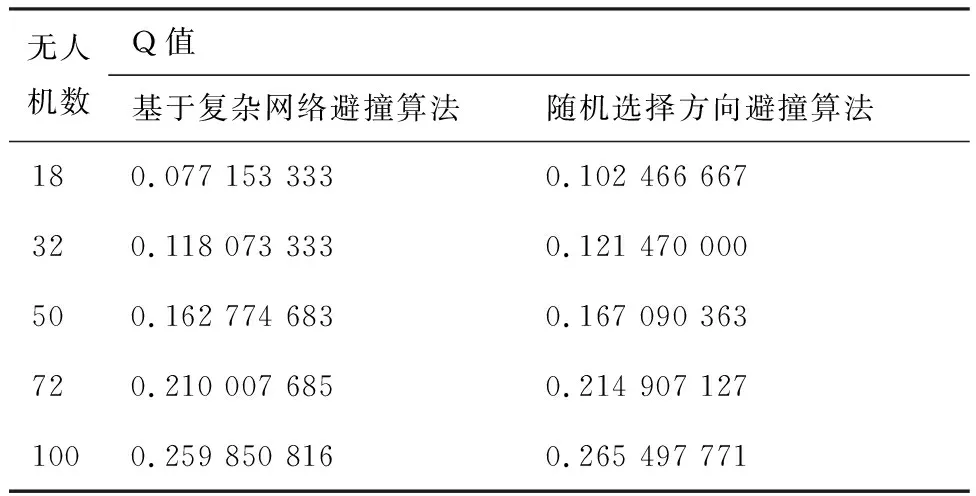
表4 2种算法的Q值比较Table 4 Comparison of Q-value of two algorithm

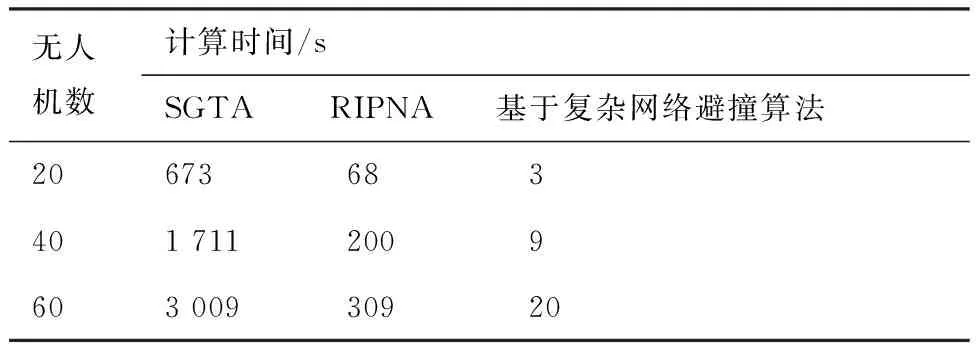
表5 不同无人机密度下的计算时间消耗Table 5 Time consumption in different UAV densities

4 总 结

提出了在局部空域内的无人机群的基于复杂网络防撞算法，该算法通过复杂网络理论将无人机的轨迹在全局范围内尽可能迅速地进行同步修改以达到避撞的效果。

进行了2个经典场景的仿真实验和大规模无人机群的仿真实验。通过2个经典无人机相遇场景下的仿真实验可以表明基于复杂网络的无人机群避撞算法是可行有效的，大规模无人机群的仿真实验表明对于不同规模的威胁密度都有很好的效果。

实验表明算法给出的避撞策略能使得原本受威胁的无人机群的安全性达到最高，从安全性的意义上看这使得无人机群的安全性和鲁棒性增强了。通过大规模无人机群的仿真验证了算法的可适用性，时间效率较其他经典算法有显著提升。未来的研究将会集中在以下方面：

1) 运用适合的启发性算法提高算法的执行效率和计算速度。

2) 对无人机群的安全性指标做更加全面的研究，将其融入现有防撞系统以提升系统给无人机群带来的安全性。

3) 考虑更加复杂的其他扰动的情况(比如强风等)以应对更加密集复杂的情况。

4) 将无人机整合到通用航空在非隔离空域内运行。