钛合金铣削刀具/工件接触区域温度预测

刘具龙，张璧，白倩,*，程博

1. 大连理工大学 精密与特种加工教育部重点实验室，大连 116024 2. 南方科技大学 机械与能源工程系，深圳 518055

钛合金(Ti-6Al-4V)由于具有比强度高、断裂韧性高、耐高温、耐腐蚀性能好等特性，广泛应用于航空航天、汽车、国防及生物医学领域[1]。然而，由于切削过程中所消耗的能量大部分转化为热能，而钛合金导热系数小，切削热不易传出，切削区温度升高，刀具磨损迅速，导致钛合金切削加工成本提高[2]。另外切削过程的热力耦合作用会引起工件加工变质层与残余应力的产生，影响已加工表面质量[3-4]。因此铣削过程刀具/工件接触区域温度预测的研究具有重要意义。

金属切削温度场预测建模中，不同工况条件下的切削热源具有不同的几何形状和热流密度，且边界条件往往是未知的，因此难以采用传统的解析法或数值法求解。目前,铣削过程温度场建模主要采用热源法，预测得到的铣削温度与实际测量结果误差较小且形式简单[5]。在铣削热源几何形状建模方面，现有研究通常将切削热源简化为直线热源[6-7]、螺旋线热源[8]及移动矩形热源[9]等。由于铣刀螺旋角的存在，直线热源虽然计算简单，但难以精确描述铣削热源，铣削温度预测存在一定误差。在铣削热源热流密度求解方面，通常热流密度通过铣削力计算获得[7-11]，能较为准确地预测铣削区域温度；然而该方法需要计算获得热流分配系数，且温度预测所需参数较多。另外部分预测模型中采用热源法对铣削温度进行预测时只考虑第1变形区对温升的影响[6-7]，忽略第2及第3变形区产生的铣削热，对温度预测模型的准确性及适用范围带来一定影响。

目前铣削温度测量方法相对较少，主要原因有[12]：① 铣削是断续切削过程，伴有刀具旋转；② 工件的热影响区域随刀具运动而移动；③ 铣削过程中产生的切屑阻碍切削区域温度测量。现有铣削过程常用的温度测量方法有热电偶法[13-14]、红外热成像法[15]以及热辐射高温计法[16]等。其中，热电偶法分为自然热电偶法、人工热电偶法和半人工热电偶法。自然热电偶法需要从旋转刀具引出热电势信号，存在较大困难且易引入附加电动势；人工热电偶法热接点较大，对变化过快的温度难以响应，不适用于直接测量铣削区域温度；红外辐射法等非接触式温度测量方法易受切屑的影响，不易获得铣削区域温度。半人工夹丝热电偶法能直接测量刀具/工件接触区域温度，且一次装夹可测量多组数据，因此本文选用该方法测量铣削区域温度。

从切削机理出发，将铣削区域的3个热源等效为螺旋线热源，热流密度计算类比铣削力预测模型中铣削力计算方法，同时考虑3个切削变形区对刀具/工件接触区域温升的综合影响，提出包含铣削热系数的热流密度计算模型并对刀具/工件接触区域温度进行预测，计算铣削温度场所需参数较少，有利于铣削区域温度的快速准确预测；通过半人工热电偶法测量刀具/工件接触区域温度，对模型的可行性与准确性进行验证。

1 铣削温度场预测模型构建

1.1 铣削传热模型简化

图1所示为铣削热源模型简化示意图，根据立铣刀结构及铣削加工原理，铣削过程工件温度场计算时，可将立铣刀沿轴向离散成无数均匀微元，每个微元的切削过程可简化为斜角切削[17](图1(a)和图1(b))，图1(c)为铣削中变形区传热示意图，铣削热主要来自3个区域(图1(b)中Ⅰ、Ⅱ、Ⅲ)[18]：① 剪切面热源区，铣削热由克服金属塑性变形所做的变形功产生；② 前刀面热源区，铣削热由切屑与前刀面的摩擦功产生；③ 后刀面热源区，铣削热由后刀面与工件的摩擦功产生。如图1(b)所示，计算工件温度场时，将3个变形区面热源等效为切削刃处的线热源，离散后的微元线热源高度为dz，长度为dL，铣刀螺旋角为β，则

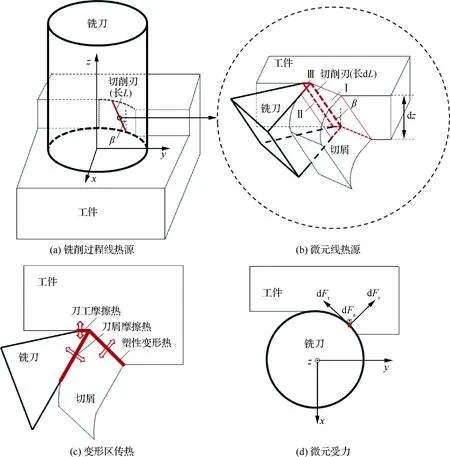
图1 铣削热源模型Fig.1 Heat source model of milling process

dL=dz/cosβ

(1)

在螺旋齿立铣过程中，瞬时切削厚度不断变化，热源热流密度随之不断变化。在刀具旋转至任一角度位置处，参与切削的刀齿各处所对应的切削厚度也不相同，热流密度呈非均匀分布。整个切削过程中，螺旋线热源长度不断变化，经历从零增至最大、从最大降至零的过程。因此，螺旋齿立铣加工传热过程可以简化为一个长度变化、热流密度非均匀且不断变化的螺旋线热源对工件加工表面周期性的断续加热过程[8]。

1.2 铣削热流密度计算

提出考虑铣削3个变形区的热流密度计算模型，该模型由铣削力与铣削速度推导得出。如图1(d)所示，铣削过程中切削力可分为3个方向的力，切向力dFt，径向力dFr和轴向力dFa，其中径向力dFr和轴向力dFa对切削温度的影响可以忽略[19]。由铣削力预测模型可以得到微元切向力计算公式为[20]

dFt=dz×(Ktc×h+Kte)

(2)

式中：h为微元的瞬时切削厚度；Ktc为切削力系数；Kte为刃口力系数，切削力系数和刃口力系数可通过实验标定获得。铣削速度为v时，每个微元的线热流密度为

qt=(dFt×v)/dL

(3)

将式(1)和式(2)代入式(3)求得

qt=cosβ×v×(Ktc×h+Kte)

(4)

(5)

则qt=qc+qe

(6)

即，总热流密度qt可分为qc和qe两部分。

当刀具足够锋利，不考虑第3变形区域时，其中切削过程中微元消耗的总功率Pt是消耗在剪切区功率Ps和摩擦区功率Pf之和[20]。此时，切削过程中微元消耗的总功率为

Pt=dFt×v=dz×Ktc×h×v=

qc×dL

(7)

因此qc由第1和第2变形区综合作用引起。

实际切削过程中，由于刀具刃圆半径及后刀面磨损的存在，在铣削力预测模型中存在刃口力系数Kte，因此qe由第3变形区引起。

将铣削热源简化为线热源时，一定范围内的每齿进给量对热量传入工件的传热比影响很小[21]。因此在每齿进给量改变而其他加工参数不变条件下，将qc和qe传入工件的比例简化为2个 固定值kc和ke，则铣削过程传入工件热量的等效线热流密度为

q=kc×qc+ke×qe

(8)

将式(5)代入式(8)求得

q=cosβ×v×kc×Ktc×h+

cosβ×v×ke×Kte

(9)

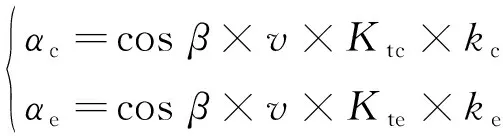
(10)

将αc和αe命名为铣削热系数，其中αc与第1、第2变形区相关，αe与第3变形区相关，将式(10)代入式(9)求得

q=αc×h+αe

(11)

当螺旋角、切削速度和轴向铣削深度等铣削参数给定时，铣削热系数αc和αe为定值，可由实验标定得到。

1.3 铣削过程工件温度场计算

工件温度场计算采用热源法，该方法基于瞬时点热源在无限大介质中的传热解析解[22]，当热源位于(x1,y1,z1)处时，点热源瞬时发热后在任意时刻τ、任意点M(x,y,z)处的温升T为

(12)

式中：R为热源点与点M距离；Q为点热源瞬时发热量；c为导热介质比热容；ρ为导热介质密度；α为导热介质热扩散系数。以瞬时点热源温升解析式为基础，按温度场迭加原理，通过对空间或时间的积分可以推导出各种形式热源的温升解析式[22]。

图2 铣削过程工件任意点M温升计算Fig.2 Calculation of temperature rise of point M at workpiece in milling process

图2所示为铣削过程中工件上任意点M温升计算示意图，本文对于铣削温度的研究所采用的铣削方式为逆铣，铣削宽度为ae，每齿进给量为fz，将时间离散，设铣削初始时刻为0，图2所示时刻为ti，根据铣刀刃数N及旋转角速度ω可知每齿所用时间tz；将铣削过程沿空间离散，此时已产生J个齿热源，每齿均匀离散为K条热源线，每条热源线时间间隔为dt，相位角差dθ，根据ti可计算总齿数J及最后一齿热源线数K1

(13)

沿轴向将每条热源线离散为S个热源点，因螺旋角存在，第s个热源点(相位角为θ)相对于螺旋线最低点存在滞后角φ，设第j个齿第k条热源线产生时间点为t，最低点相位角为φ，距观察时刻ti时间为τ，则

(14)

铣刀半径为r,铣刀侧刃刀尖处螺旋线方程为

(15)

则第j个齿、第k条热源线、第s个热源点坐标(x1,y1,z1)及该热源点dt时间内产生热量Q分别为

(x1,y1,z1)=(rcosθ,(j-1)×fz+rsinθ,

rφ/tanβ)

(16)

Q=q×dL×dt

(17)

由式(12)和式(17)可知该热源点对任意点M(x,y,z)温升影响为

(18)

而整个铣削过程螺旋线热源对点M温升影响T为所有热源点温升影响之和，即

(19)

上述计算方法要求工件介质无限大，实际铣削过程不满足该要求；然而在干切削条件下工件上表面及刀具/工件接触区域可简化为绝热边界，在与真实切削热源对称的位置设置镜像热源，即可认为温度计算满足介质无限大要求[21,23]。如图3所示，对于刀具/工件接触区域绝热边界TW，任意热源A的镜像热源位置与自身重合，热流密度大小相等，因此热源A向工件传热的热流密度为2q，引起任意点M温升为2T；对于工件上表面绝热边界WA设置镜像热源A′，热源A′向工件传热的热流密度为2q′，引起点M温升为2T′，其中q与q′大小相等；铣削过程ti时刻工件点M温度可等效为运动螺旋线热源与其对应镜像热源在该点引起的温升加上初始温度T0，即

Ti=2T+2T′+T0

(20)

点M温升计算流程如图4所示，首先输入切削参数和刀具尺寸，根据切削参数可计算铣削过程切入切出角θst及θex。将铣削过程在时间上进行离散，计算ti时刻任意点M的温度Ti。由ti可计算出已切削齿数J,将每齿热源在空间上进行离散，沿铣刀旋转方向离散为K条螺旋线热源，沿铣刀轴向离散为S个点热源。根据热源点相位角θ判断该热源点是否在切入切出角范围内，若不在范围内，则温升dT为0，计算下一个热源点产生的温升；反之则依据该热源点坐标及相位角计算切削厚度h及热流密度q，从而得到该热源点对点M产生的温升dT，将各热源点温升累加即可求得ti时刻点M温升，选取不同时间点ti重复计算，最终获得点M温度随时间的变化。

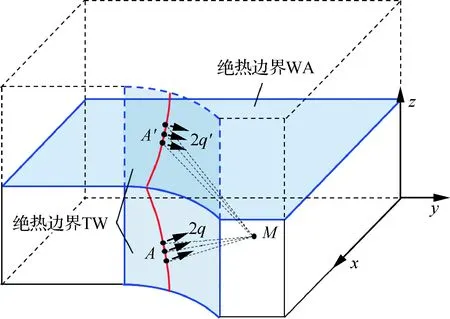
图3 螺旋线以及镜像热源Fig.3 Spiral-line and mirror-image heat source

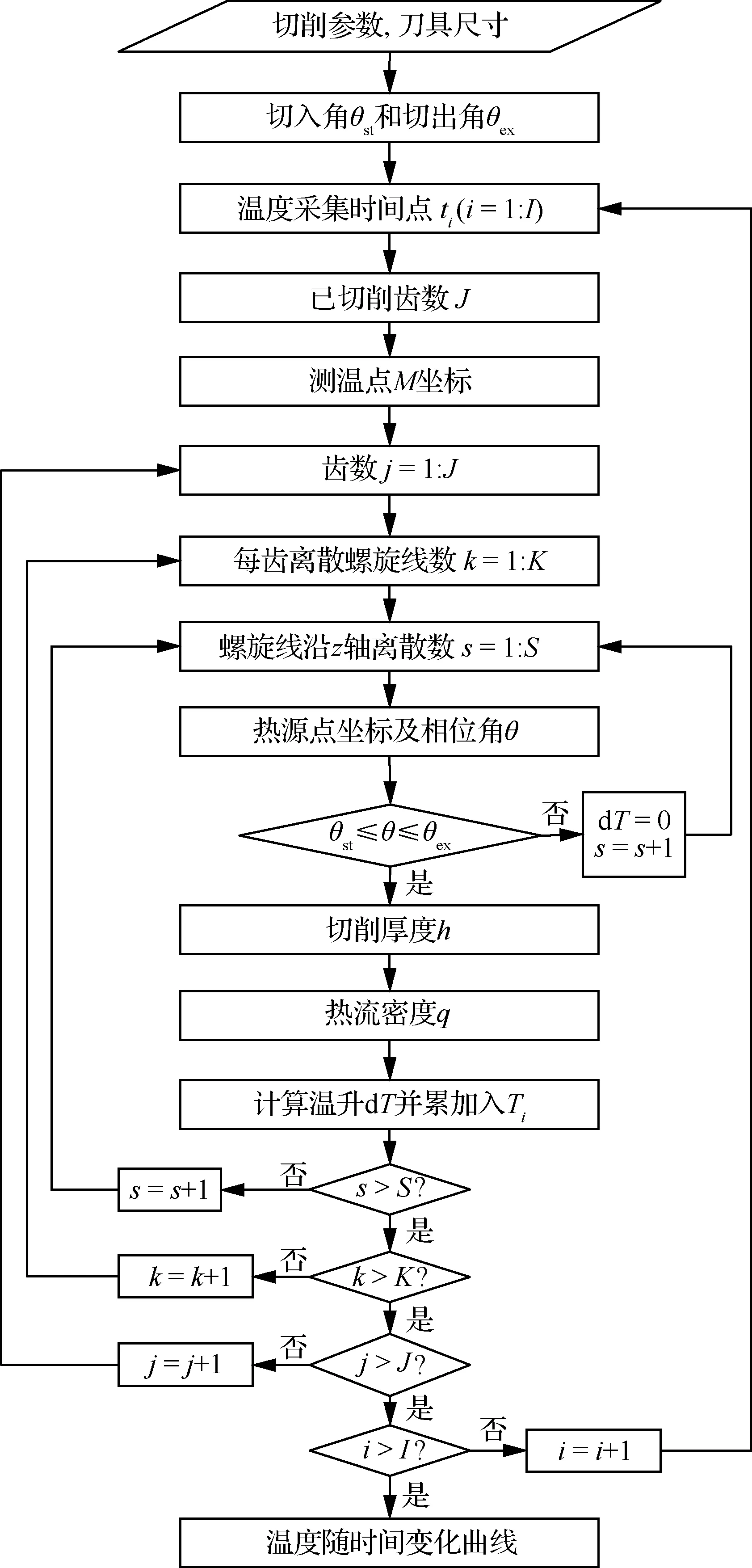
图4 铣削过程工件温度场计算流程Fig.4 Flow chart of calculation of workpiece temperature field in milling process

2 铣削热系数标定方法

在以往的铣削温度研究中，铣削过程热量传入工件的传热比kc和ke是很难确定的参数，不同的加工材料、刀具和切削参数对传热比都有影响[21]，因此受传热比影响的铣削热系数αc和αe同样难以确定。推导得出热流密度计算式(11)与微元铣削力预测式(2)相似，因此可以参考切削力系数和刃口力系数的标定过程[20]对铣削热系数αc和αe进行标定。

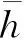
(21)

将式(11)沿接触角进行积分再除以接触角可得到平均热流密度为

(22)

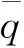
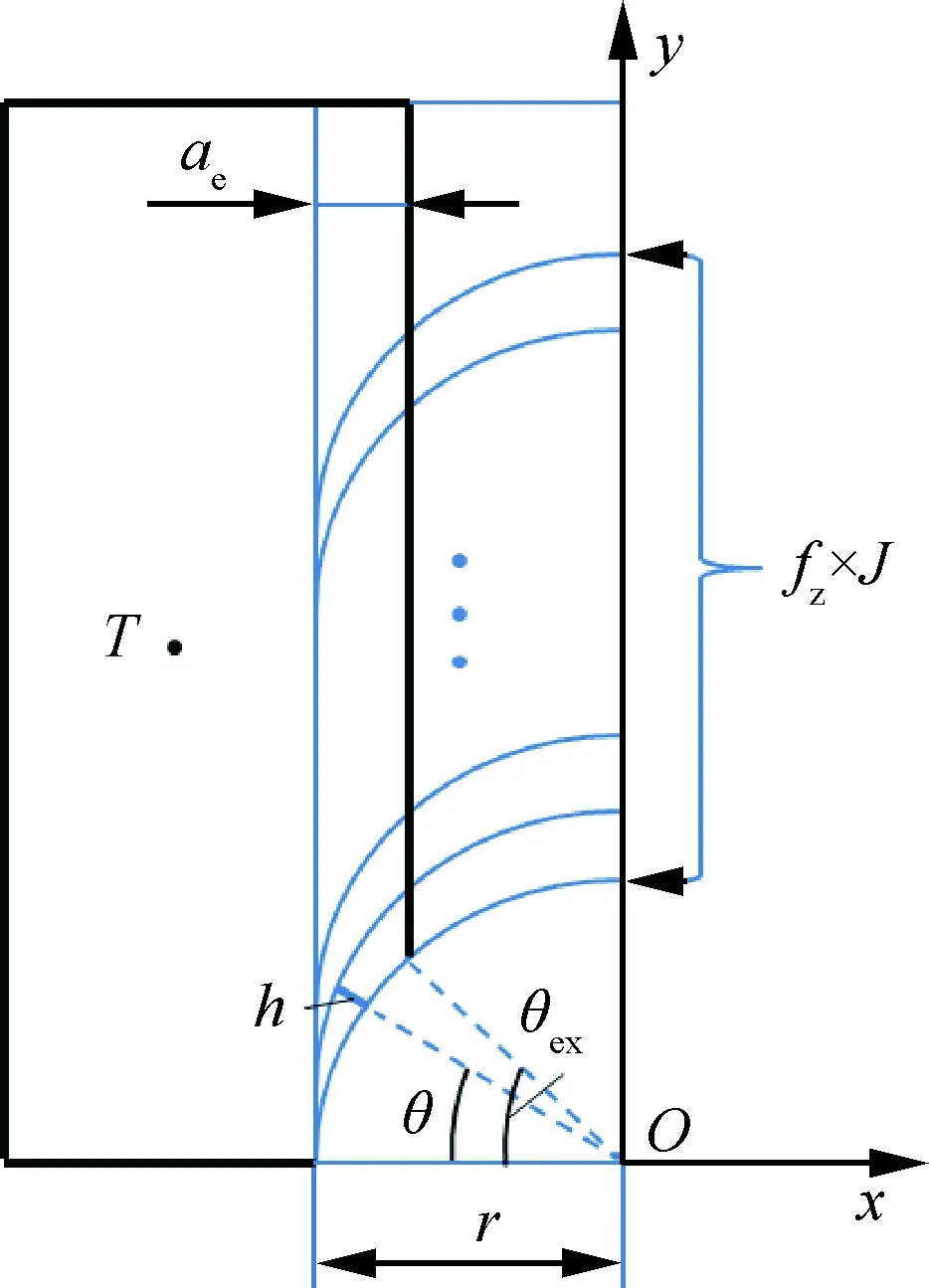
图5 铣削热系数标定Fig.5 Calibration of milling heat coefficients

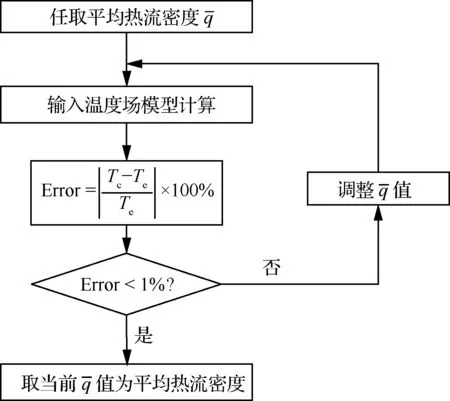
图6 反求平均热流密度流程Fig.6 Flow chart of reversing average heat flux density

3 实验设备与方案

3.1 铣削热系数标定实验

为了确定铣削热系数从而获得铣削热流密度，在不同的每齿进给量条件下进行铣削实验。实验机床为凝华数控雕铣机NHX650；实验刀具为株洲钻石切削刀具股份有限公司生产的PML-2E-D6.0整体硬质合金两刃铣刀，刀具直径6 mm；工件材料为钛合金Ti-6Al-4V轧制板材，尺寸为100 mm×50 mm×12 mm。测温仪器包括线径0.1 mm型号为TT-J-36的J型热电偶和NI公司生产的NI9213采集卡。

为保证实验和计算的可靠性及准确性，在相同铣削参数下，于工件表面设置3个测温点T1、T2及T3，3个点与待加工侧面的距离相等，对3个 点的温度进行测量并分别计算对应的平均热流密度。如图7所示，将3个J型热电偶焊接在距离待加工侧面一定距离处，实际精确距离通过ImageJ对照片进行测量得到；为减小空气对流影响，在热电偶焊接点上方贴上高温胶带；铣削过程中利用LabVIEW软件通过测温仪器测量3点温度。铣削加工参数如表1所示。

图7 铣削热系数标定实验Fig.7 Calibration experiment for milling heat coefficients

表1 铣削热系数标定实验铣削参数

Table 1 Parameters for calibration ofmilling heat coefficients

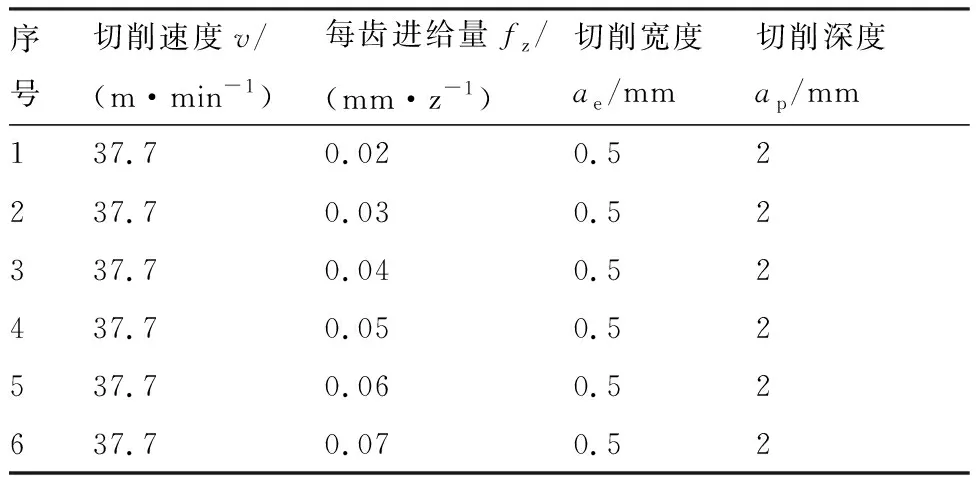
序号切削速度v/(m·min-1)每齿进给量fz/(mm·z-1)切削宽度ae/mm切削深度ap/mm137.70.020.52237.70.030.52337.70.040.52437.70.050.52537.70.060.52637.70.070.52

3.2 刀具/工件接触区域测温实验

为验证钛合金铣削过程中的工件温度场预测模型，在铣削实验中采用半人工热电偶进行刀具/工件接触区域温度测量。工件材料为2块钛合金Ti-6Al-4V轧制板材，尺寸为40 mm×40 mm×12 mm。测量热电势的数据采集卡采用NI公司生产的NI6320采集卡。采用0.01 mm厚度的天然云母片保证工件1和工件2绝缘，0.1 mm厚度的康铜丝(J型热电偶的负极丝)作为半人工热电偶的负极。室温下康铜导热系数为22.7 W/(m·K)[24]，钛合金Ti-6Al-4V导热系数为6.8 W/(m·K)[25]，天然云母导热系数为2 W/(m·K)[26]。

图8(a)所示为半人工热电偶测温原理图，康铜丝1水平穿过工件1、2且与刀具进给方向垂直，康铜丝1与工件上表面存在一定距离；工件、夹具和康铜丝1之间通过绝缘材料两两绝缘；康铜丝2焊接在工件1的远端作为冷接点；铣刀沿进给方向以速度vf进给，转速为n。当铣刀切过绝缘层时，工件1与康铜丝1之间的绝缘层被破坏，从而搭接形成热电偶的热接点，利用测温仪器可测得冷、热接点间的电动势。康铜丝与钛合金组成的热电偶为非标准热电偶，需对其电动势与温度之间对应关系进行标定，通过标定关系式可得热接点温度，即铣削过程刀具/工件接触区域温度。

采用半人工热电偶测量铣削区域温度过程中，热接点并非固定点，如图8(b)所示，铣刀未切削康铜丝时，热接点为M1；铣刀切削康铜丝时，每切过一齿，热接点Mn向工件已加工侧面移动一段距离；铣刀远离康铜丝时，热接点为MN。

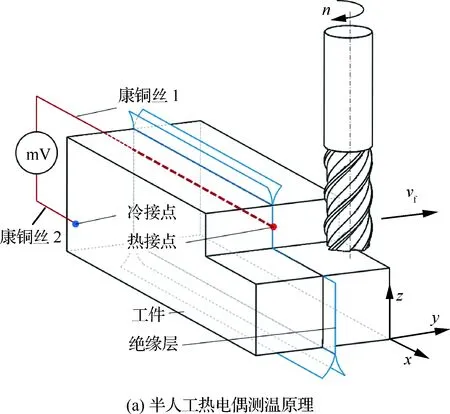
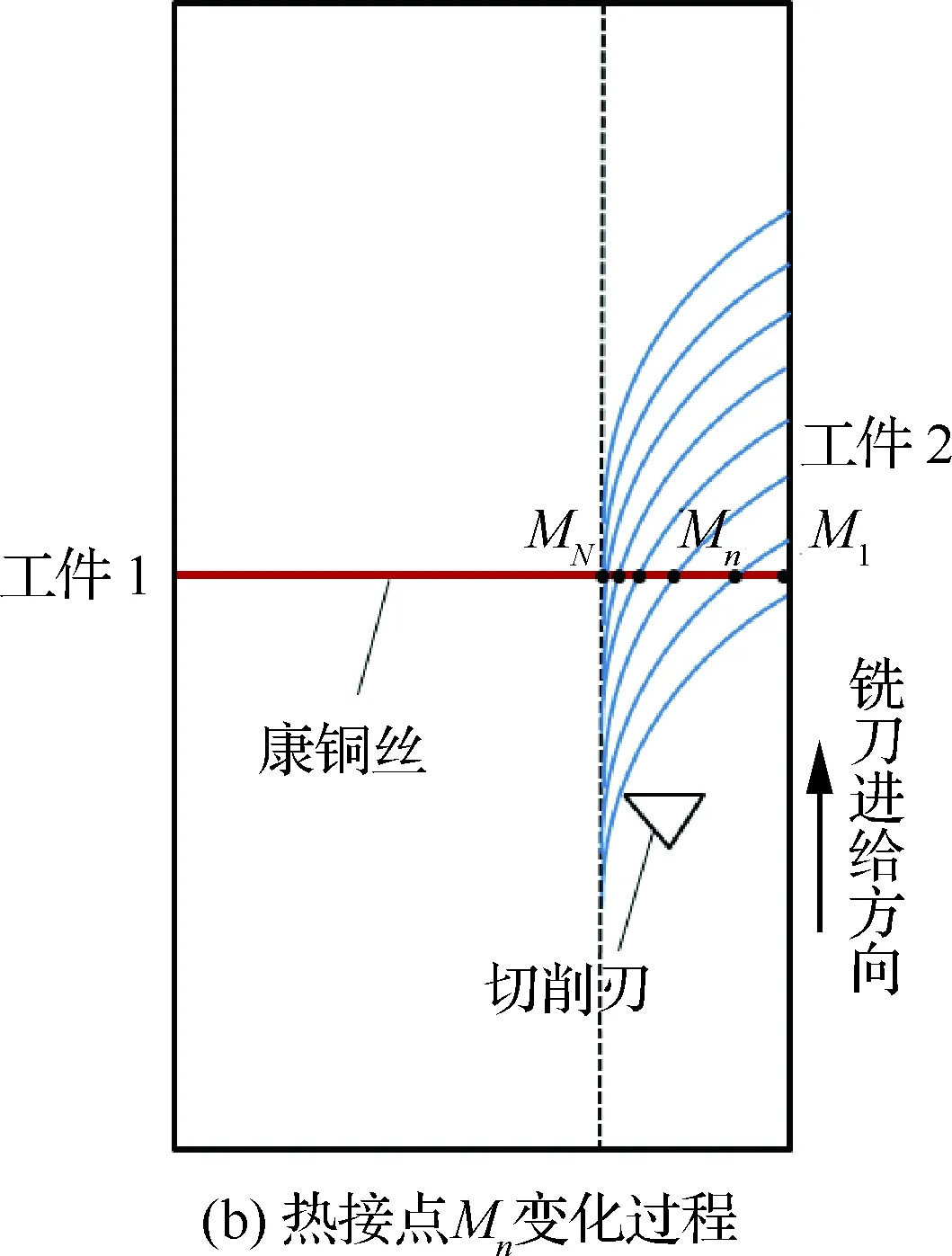
图8 半人工热电偶测温原理Fig.8 Temperature measuring principle of semi-artificial thermocouples

由于云母片和康铜丝存在，两块拼接而成的钛合金工件和整体工件在铣削过程中温度场是有差异的。为研究拼接工件对温度场及测量结果的影响，设计如下实验，图9所示为实验装置图，工件及云母片装夹方式如半人工热电偶测温原理所示(见图8(a))，不同之处为康铜丝与工件上表面平齐而非置于距上表面一定距离处；将直径0.1 mm 的J型热电偶焊接在工件上表面处，热电偶焊接完成后，焊点与云母片的距离D1通过ImageJ对图片分析得到，焊点存在一定的体积，为保证实验可重复性，每次实验取其中心作为测量基准；测量焊点与待加工侧面的距离D2，再通过铣削保证每次实验前距离D2为1.7 mm；为降低空气对流影响，在焊点上覆盖一层热熔胶。实验中切削速度、每齿进给量和切削深度如表2所示，切削宽度为0.4 mm，铣削方式为逆铣，铣削过程中测量得到工件上表面焊点处最高温度，将其与采用整体工件相同参数下所测最高温度比较，分析拼接工件对温度场及测量结果影响。

图10所示为拼接工件与整体工件对铣削温度场影响实验结果，铣削过程中工件1测温点的最高温度随云母片距离D1减小而逐渐升高，温升相对误差小于15%，与整体工件温度测量值相差不大，因此可以采用拼接工件对钛合金铣削过程进行半人工热电偶温度测量。

图11所示为采用半人工热电偶的刀具/工件接触区域测温实验装置图，热接点康铜丝1水平穿过工件1和2且工件和康铜丝之间通过云母片绝缘，冷接点康铜丝2焊接在工件1的远端，工件和夹具通过云母纸绝缘。铣削方式为逆铣，铣削过程测量半人工热电偶冷、热接点的热电势。为保证实验数据有效且切削宽度准确，在正式实验之前铣平工件，同时破坏康铜丝与工件间绝缘层，使热电偶、工件及采集卡形成闭合回路。热接点在切削后不会断开，在正式实验中铣刀未切削康铜丝时闭合回路依然存在，可以测得冷、热接点的热电势。其中铣削加工参数如表2所示。

图9 拼接工件对温度场影响实验Fig.9 Experiment on influence of splicing workpieces on temperature field

表2 刀具/工件接触区域测温实验铣削参数Table 2 Milling parameters for temperaturemeasurement of tool/workpiece contact zone

序号切削速度v/(m·min-1)每齿进给量fz/(mm·z-1)切削宽度ae/mm切削深度ap/mm137.70.040.22237.70.040.32337.70.040.42437.70.040.52537.70.040.62

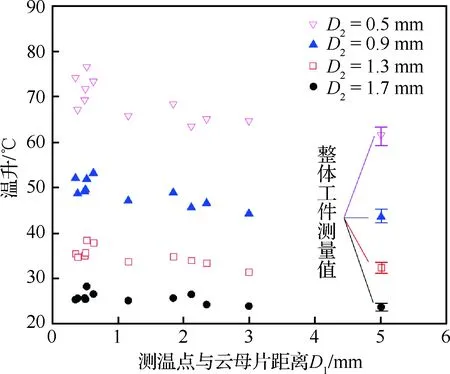
图10 拼接工件与整体工件对温度场的影响Fig.10 Effect of splited workpieces and whole workpiece on temperature field

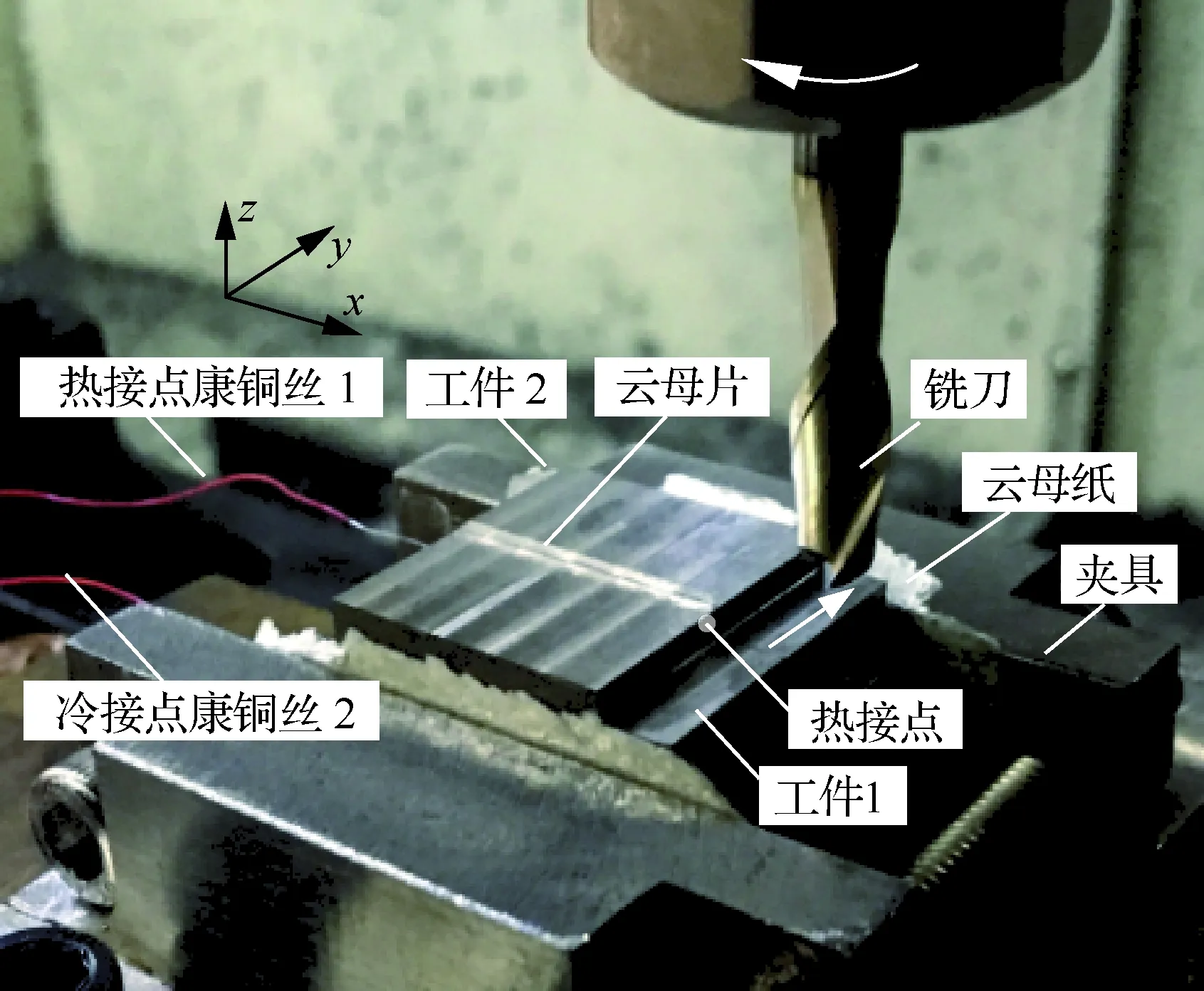
图11 刀具/工件接触区域测温实验Fig.11 Temperature measuring experiment of tool/workpiece contact zone

为了获得Ti-6Al-4V工件和康铜丝组成的半人工热电偶冷、热接点温差与热电势的对应关系，使用英国GSI Lumonics公司的连续Nd:YAG激光器作为热源，对钛合金工件进行加热然后测量冷、热接点温度及热电势(见图12)。将两个J型热电偶焊接在工件两端分别作为热接点和冷接点，采用150 W激光照射热接点附近工件使热接点温度升高，激光运动方向如图12所示，此过程中同时测量冷、热接点温度及康铜丝之间热电势信号。调整激光照射点位置使其与热接点之间最短距离逐渐变小，进行多次实验采集实验数据，直至热接点最高温度达到900 ℃。

标定时，冷接点温度即参考温度为室温，与半人工热电偶测温实验的冷接点温度一致，最终得到钛合金-康铜热电偶的温度T(℃)与电势U(mV)对应关系为

T=2.573×10-3×U3-3.015×10-1×U2+

27.43×U+23.19

(23)

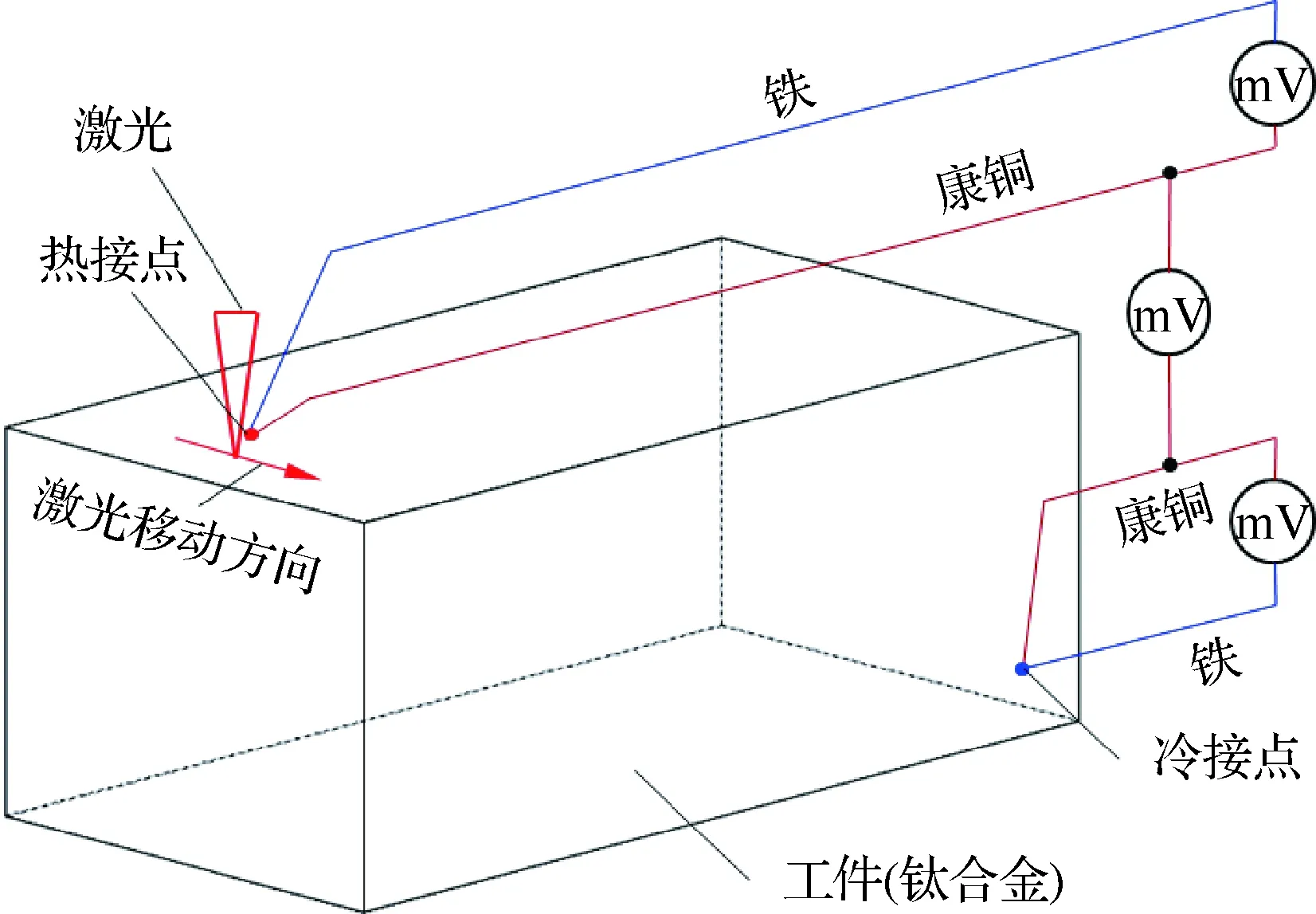
图12 半人工热电偶标定Fig.12 Calibration of semi-artificial thermocouples

4 实验结果分析与讨论

4.1 铣削热系数标定实验结果分析

刀具/工件接触区域测温实验中，铣削方式为逆铣，铣削宽度小于铣刀半径，切削刃切入工件实际切削厚度h由0增至最大然后切出工件，本文实验所选参数下最大实际切削厚度为0.024 mm，因此将拟合直线分别延伸至0和0.024 mm处，如图14所示，本文温度场计算中假设在此切削厚度范围内热流密度随切削厚度增加线性增加。为保证预测准确性，对铣削温度进行预测时，最大切削厚度不应超过标定厚度最大值20%。当某切削参数下最大切削厚度小于标定的最小平均厚度时，因刃圆半径的存在，理论切削厚度与实际切削厚度相差过大，标定值不再适用，因而需扩大标定范围。

图13 采用平均热流密度所预测的温度与 实验温度对比(fz=0.03 mm)Fig.13 Comparison of predicted temperature by average heat flux density and experimental temperature (fz=0.03 mm)

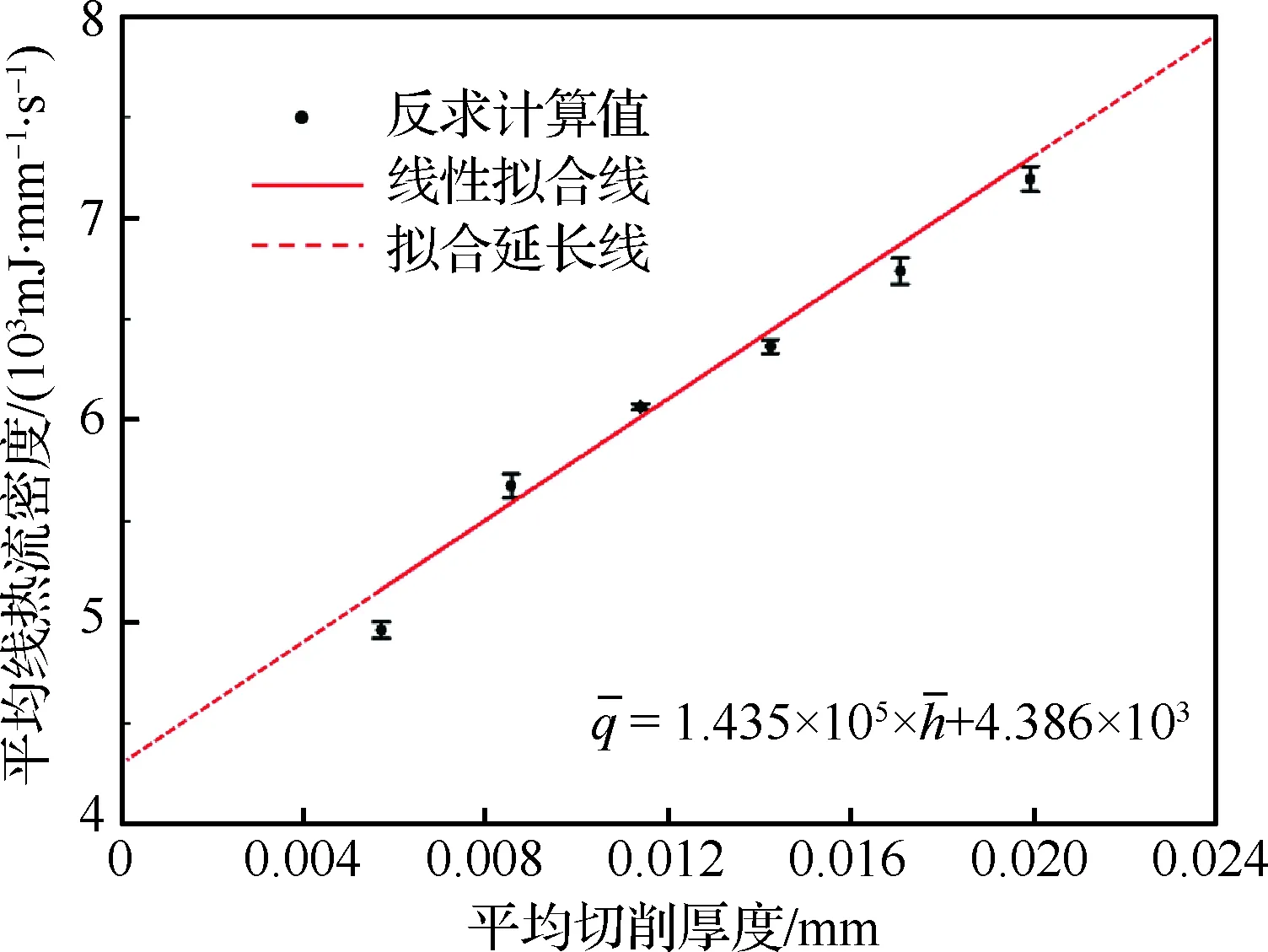
图14 铣削热系数拟合Fig.14 Fitting of milling heat coefficients

4.2 测温实验结果分析及温度场模型验证

将半人工热电偶测温实验测得热电势通过标定关系式转换可得到实际铣削温度。如图15(a)所示为ae=0.4 mm，fz=0.04 mm切削参数下铣削温度预测值与实验值，从图中可以看出预测结果与实验结果具有相同趋势：0至0.37 s时间段内，铣刀逐渐接近测温点，温度从室温25 ℃缓慢升高；0.37 s至0.95 s时间段内，铣刀切削热电偶丝，测温点不断改变，温度剧烈变化，实验温度中上包络线最大值为310 ℃，下包络线最大值为70 ℃，预测温度中上包络线最大值为306 ℃，下包络线最大值为86 ℃；0.95 s至1.5 s时间段，温度逐渐下降。铣刀切削电偶丝时所测温度上包络线反映了切削刃在经过一个切削弧区的过程中刀具/工件接触区域的温度变化情况，下包络线反映了工件在断续切削过程中铣刀未接触工件时切削弧区的温度[27]。上包络线温度随切削时间降低，原因是热接点在铣削进程中所处切削位置不同，切削厚度逐渐减小(图8(b))，因此温度逐渐降低。实验值下包络线温度比预测值低，原因为实验过程中存在空气对流等影响，导致测量温度较低。

图15(b)所示为半人工热电偶测温实验中实验与预测温度最大值对比结果，固定其他切削参数，切削宽度从0.2 mm增加至0.6 mm，实验所测温度最大值从283 ℃增加至360 ℃，预测温度最大值从275 ℃增加至329 ℃。通过对比分析发现实验值与预测值整体趋势一致，但各个加工参数下，实验值与预测值并非完全相同，总体情况为实验最大温度高于预测最大温度，主要可能有两个方面原因，一是理论计算中存在简化，未考虑空气对流，影响预测精度，二是测温实验中云母片导热系数低于钛合金，拼接工件相较于整体钛合金散热条件变差。

各切削参数下实验值与预测值相对误差均在10%之内，说明本文热流密度计算公式及刀具/工件接触区域温度预测模型具有较高的准确性。

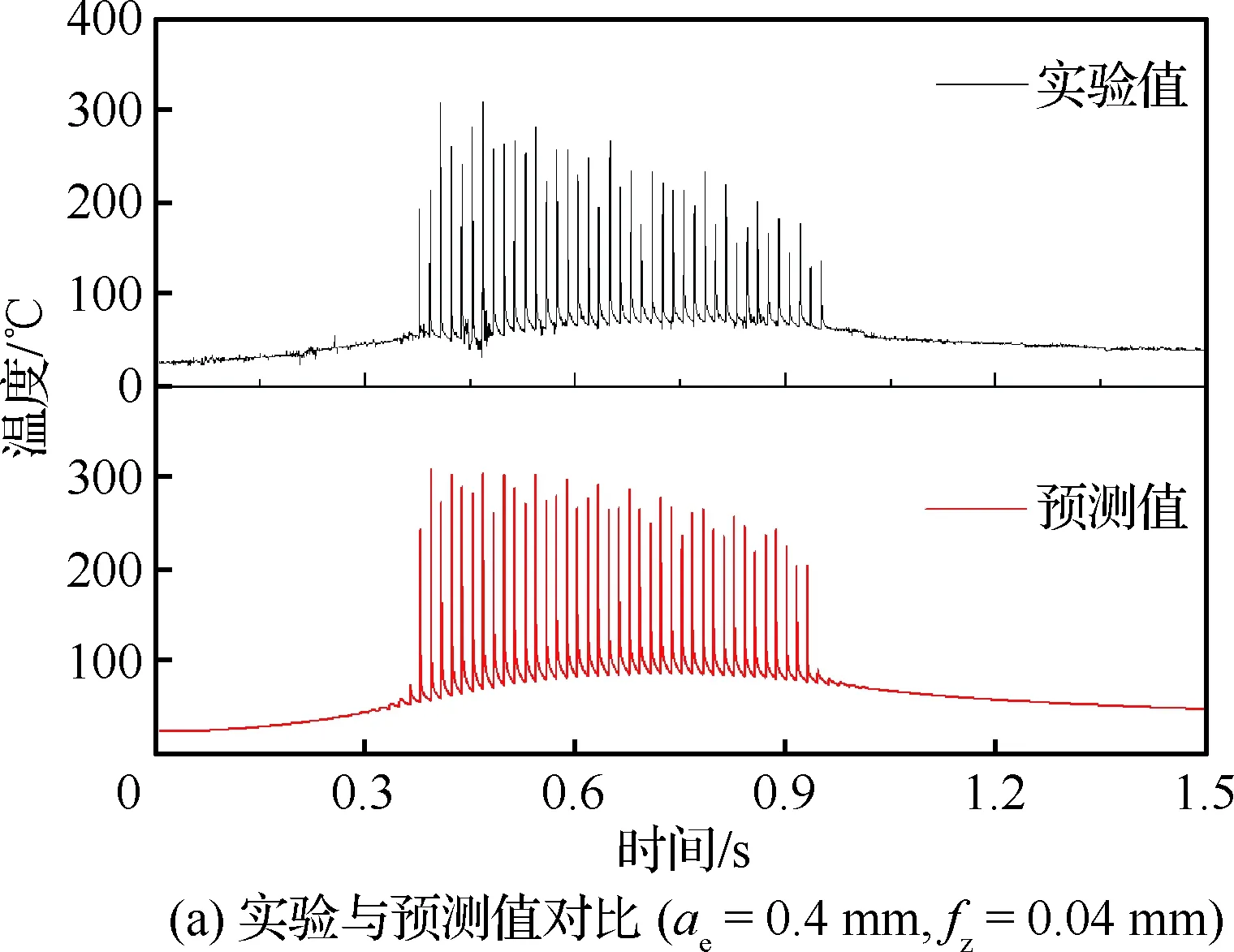
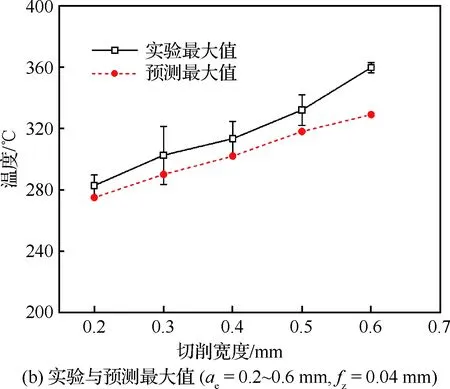
图15 半人工热电偶测温结果Fig.15 Temperature measurement results by semi-artificial thermocouples

5 结 论

1) 将铣削热源简化为螺旋线热源时，在切削厚度为0.05～0.20 mm范围内，热流密度随切削厚度增加接近于线性增加，相关系数达到0.981。

2) 建立的铣削区域温度预测模型预测值与实验值的相对误差在10%之内，具有较高的准确性。

3) 通过对比分析实验值与预测值，可以发现铣削温度在切削宽度0.2～0.6 mm范围内随切削宽度的增加而增加。