基于可达集方法的结冰飞机着陆阶段安全风险评估

武朋玮，李颖晖，郑无计，周驰，董泽洪

空军工程大学 航空工程学院，西安 710038

飞机着陆是整个飞行过程中飞行员参与控制的重要环节之一，对于考虑人为因素的安全性分析有重要意义。波音公司统计数据显示，2003—2012年全球全重27 216 kg以上的商用喷气飞机相关事故中，23%的严重事故和17%的事故死亡人数发生在着陆阶段[1]。着陆阶段飞机的飞行高度较低，如果飞机状态出现不稳定，飞机调整状态的时间非常短，另外由于飞机着陆过程中会遭遇风切变和微暴流，更易使飞机发生危险，因此飞机着陆阶段的安全性问题尤为突出。

飞机的安全飞行是航空工业发展中不可忽视的重要问题，而造成飞机失事的原因有很多，其中，结冰就是主要原因之一。自从固定航线出现以来，结冰造成的灾难性后果就不断困扰着人们。飞机着陆时高度下降，会穿过云层等易发生结冰的环境。一旦机翼或尾翼结冰，将有可能造成飞机失速坠毁，此类事故曾经多次发生并且造成惨重的后果。2001年1月4日，两架运-8飞机在着陆过程中因尾翼结冰相继坠毁，造成12名机组成员和6名地面人员死亡，2人受伤。2009年美国科尔根航空公司3407号航班的DHC-8飞机在夜间仪表进近着陆过程中，由于飞机飞行速度低于结冰后的失速速度，驾驶员操纵不当引发重大飞行事故，造成50人遇难[2]。

目前各种大飞机都使用防/除冰装置来应对结冰现象，然而由于防/除冰装置体积和质量比较大，防/除冰效果有限，难以从根本上解决结冰的影响。另外，根据飞机的动力学特性和结冰后飞行特性的改变，从控制稳定上应对结冰后飞机失稳的方法正在逐渐发展，并有望成为解决结冰对飞行影响的有效手段。ATR-72等飞机为应对结冰对飞行性能的影响，通过改进飞行边界控制保护系统，考虑最严重结冰情况并制定对应的边界保护限制，当飞机遭遇结冰，结冰保护系统就开始工作[3-4]。美国伊利诺伊州立大学的Bragg等提出了“飞机智能防冰系统”的设想[5-6]。NASA Glenn研究中心启动智能防冰计划，开展控制与传感、安全性、空气动力学等学科组合的系统研究，并通过飞行试验进行了验证[7]。国内一些大学和科研机构也针对飞机结冰后稳定包线的改变进行研究，对结冰模型和结冰影响进行分析，提出了有关结冰参数辨识的研究方案。

可达集方法最初用于研究变化的流体外形，近年来利用可达集方法开展飞行安全分析得到一定的应用。文献[8]利用水平集方法对飞机的自动着陆过程进行安全性分析，文献[9]以飞机的筋斗动作为研究对象分析飞机机动过程中的可达集包线，文献[10]将可达集方法用于四旋翼飞行器的后翻机动安全操纵范围的确定中，分析不同模式下状态参数的约束条件及其对应的可达集。

本文建立了飞机结冰前后的纵向动力学质点模型，运用可达集理论分析不同结冰程度下的四维可达集，得到飞机的飞行安全包线。从理论上说明结冰影响飞行安全的机理，对结冰飞机的着陆操纵提出指导，达到飞机在结冰状态下安全着陆的目的。通过统计学方法确定极值理论所需的关键参数，建立飞机风险概率计算模型，根据可达集结果提取的航迹倾角和速度组成的安全包线，分析不同结冰条件下的风险概率。根据结冰风险概率对驾驶员操纵提出指导，创新地提出利用可达集评估结冰风险，所得的风险评估结果对于研究结冰引起的飞行安全和适航性问题具有重要意义。

1 飞机纵向质点动力学模型

本文选择双水獭飞机为研究对象，其模型数据参考文献[11]。设飞机为刚体，为简化研究，在不考虑纵向和横航向耦合基础下，提取飞机纵向动力学质点方程，以纵向的速度、航迹倾角、俯仰角速度和迎角4个参数展示飞机纵向运动的变化，其动力学方程[12]可写为

(1a)

(1b)

(1c)

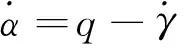
(1d)

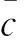
由于结冰对飞机动力学的影响非常复杂并且结冰条件多种多样，运用飞行试验获得飞机结冰条件下的气动参数难以实现，而采用结冰影响模型的方法评估飞机结冰严重程度具有一定科学性并且简单实用。因此本文采用结冰影响模型分析结冰前后飞机气动导数的变化。

飞机结冰前后的气动导数变化可表示为[13]

CA(iced)=(1+ηkiced)C(A)

(2)

式中：C(A)为飞机干净翼型下的某个气动导数值；CA(iced)为飞机发生结冰之后的气动导数值；kiced为某个气动参数受结冰影响的程度；η为结冰程度的大小，不结冰时其值为零，η随结冰程度增加而增加。

2 可达集计算

飞行器的动态特性可用常微分方程描述为

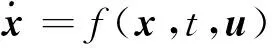
(3)

式中：x∈Rn表示n维状态变量；u∈U表示系统的输入变量。

系统的初始状态受控制量u∈U的作用，如果能够在一定时间t∈[0,τ]内到达目标集，这些所有初始状态的集合就是反向可达集[14-15]。

在分析系统方程时，由上述目标集的说明可知，可达集内的状态都能够在某一控制下经过给定时间后进入目标集，而可达集外的状态则无论经过什么控制，都不能在给定时间内进入目标集。如图1所示，B点和C点都是可达集内的状态点，在某一控制量作用下，经过一定时间最终会进入目标集并停留，而可达集外的状态点A无论在怎样的控制作用下都无法进入目标集。

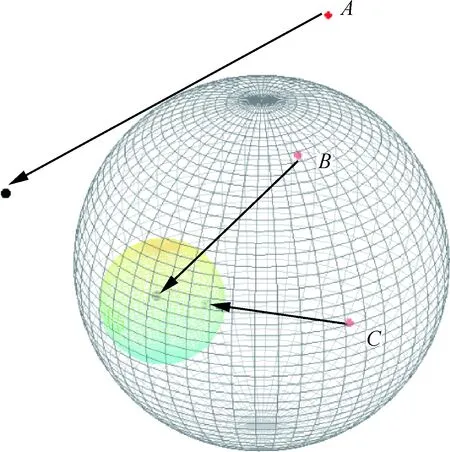
图1 目标集与可达集的关系Fig.1 Relationship between object set and reachability set

水平集方程可以表示为

(4)

式中：φ(x,t)为水平集函数。

目标集G0可由水平集函数表示为

G0={x∈Rn|φ(x,0)≤0}

(5)

通过计算如下Hamilton-Jacobi方程的黏性解能够得到目标集G0对应的可达集

(6)

式中：Hamilton函数H(x,p)为

(7)

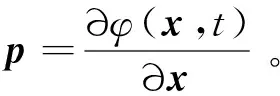
u*(x,p)=arg maxpTf(x,t,u)

(8)

关于可达集理论的介绍，以及可达集的求解过程和步骤分析可参考文献[9]。

3 飞机着陆阶段分析

3.1 飞机着陆参数

飞机在着陆过程中，发动机推力T为飞机着陆的一个输入控制量，假定发动机推力方向与飞机航迹方向一致；另一个输入控制量是飞机的俯仰舵偏角。发动机推力和飞机俯仰舵偏角都有取值限制，由于结冰程度的影响，迎角最大值即失速迎角会改变。

在下滑阶段，飞机沿着下滑斜率飞行，并且下滑角度必须保持在理想下滑倾角的变化范围内，因此航迹倾角的取值范围是[γmin,γmax]，并且γmin=γ0-dγ，γmax=γ0+dγ，γ0为理想的航迹角。在着陆过程中的速度也有限制，着陆速度超过最大限制会对飞机结构造成损坏，可能引起飞机冲出跑道的危险；而着陆速度超出最小限制会造成失速，失速速度可表示为

(9)

式中：ρ为空气密度；CLmax为最大升力系数。速度范围取为不同结冰程度下的安全速度限制，高度则根据实际着陆情况，确定在一定正值范围内。

综上所述，将着陆即将结束时刻的状态范围定义为目标集。如表1所示，不同的结冰程度对应飞机着陆不同的失速速度和失速迎角，根据飞机着陆可承受的冲击得到着陆允许的最大速度。

表1 参数取值范围Table 1 Range of parameters

3.2 飞机着陆可达集

由式(7)得到动力学模型下的Hamilton函数为

(10)

式中：p1、p2、p3、p4分别为φ(x,t)对状态V、γ、q和α的偏导。最优控制量的取值是通过将输入的不同取值组合代入到系统中计算可达集，并对可达集大小进行比较得到的。最优控制量的选取可以通过计算机的仿真试验进行，同时进行多组输入得到最大的可达集，最大的可达集对应的输入被视为最安全的操纵指令。这一指令指导驾驶员操纵飞机，使飞机达到最安全的飞行状态。

目标集是根据速度、航迹倾角、俯仰角速度和迎角的合理范围确定的，而可达集由目标集扩展而成，飞机着陆状态在这一范围内是稳定和安全的。可达集的状态经过一定的时间会进入目标集，一旦状态偏离可达集范围，飞机状态在任何输入条件下都无法进入目标集，着陆将不能达到安全状态。

为将可达集结果可视化显示，在着陆安全包线的计算分析过程中，选取状态的3项参数作为性能指标，构建一个三维可视图形，根据图形的区域范围确定安全包线的范围。本文将状态参数迎角切片进行数据分析，选取速度、航迹倾角和俯仰角速度作为求解目标函数。

首先计算结冰程度为0时给定目标集下的反向可达集，其对应的失速迎角为17.5°，结果如图2 所示，网格内部的蓝色部分为给定的目标集，黄色网格所包围的区域是对应的可达集。以着陆下滑结束段的安全状态为起始状态，对飞机着陆阶段的飞行状态模型进行反时间方向的求解，所得的可达集为飞机的飞行安全包线。

在计算所得的可达集范围内，任何一个状态点都能够通过合理的操纵，进入理想的目标集内。当飞机状态偏离可达集范围时，飞机在任意操纵下均无法到达理想的着陆飞行状态。因此，驾驶员操纵或机载计算机的控制律应该确保飞机状态始终位于可达集内。从图2中看出，未结冰时，飞机的安全飞行状态空间较大，飞机的安全裕度较大，驾驶员的安全操纵范围也较大。

可达集刻画的结果是存在误差的，误差主要由计算网格数目决定。网格数目越多，计算精度越高，误差相对较小，计算机的计算时间增长。为使计算时间缩短，同时计算精度误差相对于飞行安全范围能够忽略，应选取合适的网格数目进行计算。

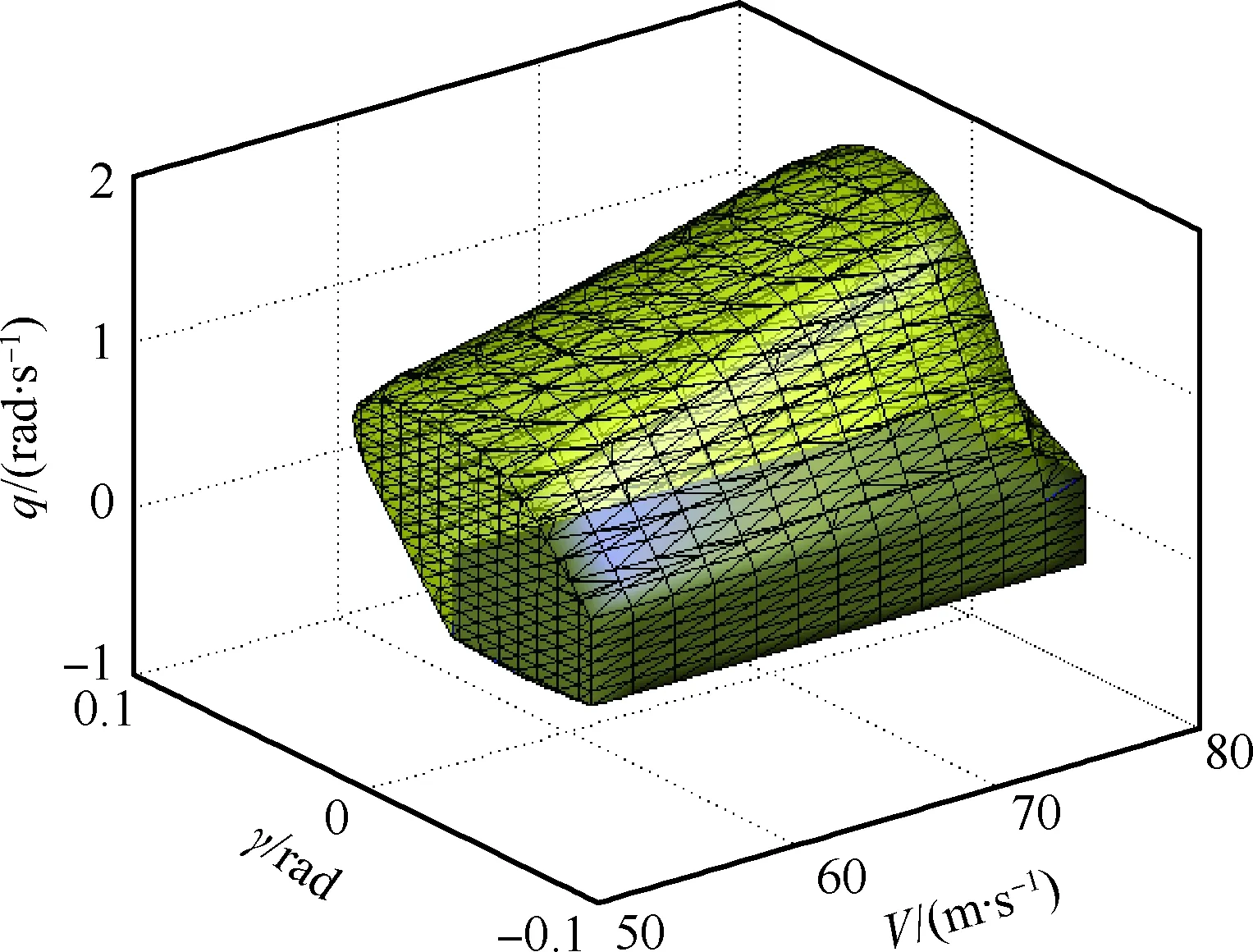
图2 结冰程度为0时目标集与可达集Fig.2 Object set and reachability set when icing degree at 0

结冰程度不同时，对应的失速迎角等变量限制也不同。结冰程度是0.1时的失速迎角为16.9°，结冰程度是0.2时的失速迎角为15.25°，因此需要在不同控制和不同的目标集下进行计算。另外，结冰会导致飞机的气动导数发生变化，因此不同结冰程度的可达集有明显的差异，其仿真结果如图3和图4所示。

图3中，黄色网格部分为结冰程度为0.1时的可达集，红色部分为不结冰飞机的可达集。可以看出，结冰后飞机的安全包线缩小，可达集范围收缩，驾驶员可以安全操纵的区域变小，安全裕度降低。图4中，黄色网格部分为结冰程度为0.2时的可达集，红色部分为结冰程度为0.1时飞机的可达集。可以看出，随着结冰程度的增大，可达集缩小，安全驾驶范围缩小，飞机的操纵需要更加谨慎，发生危险的概率增加。

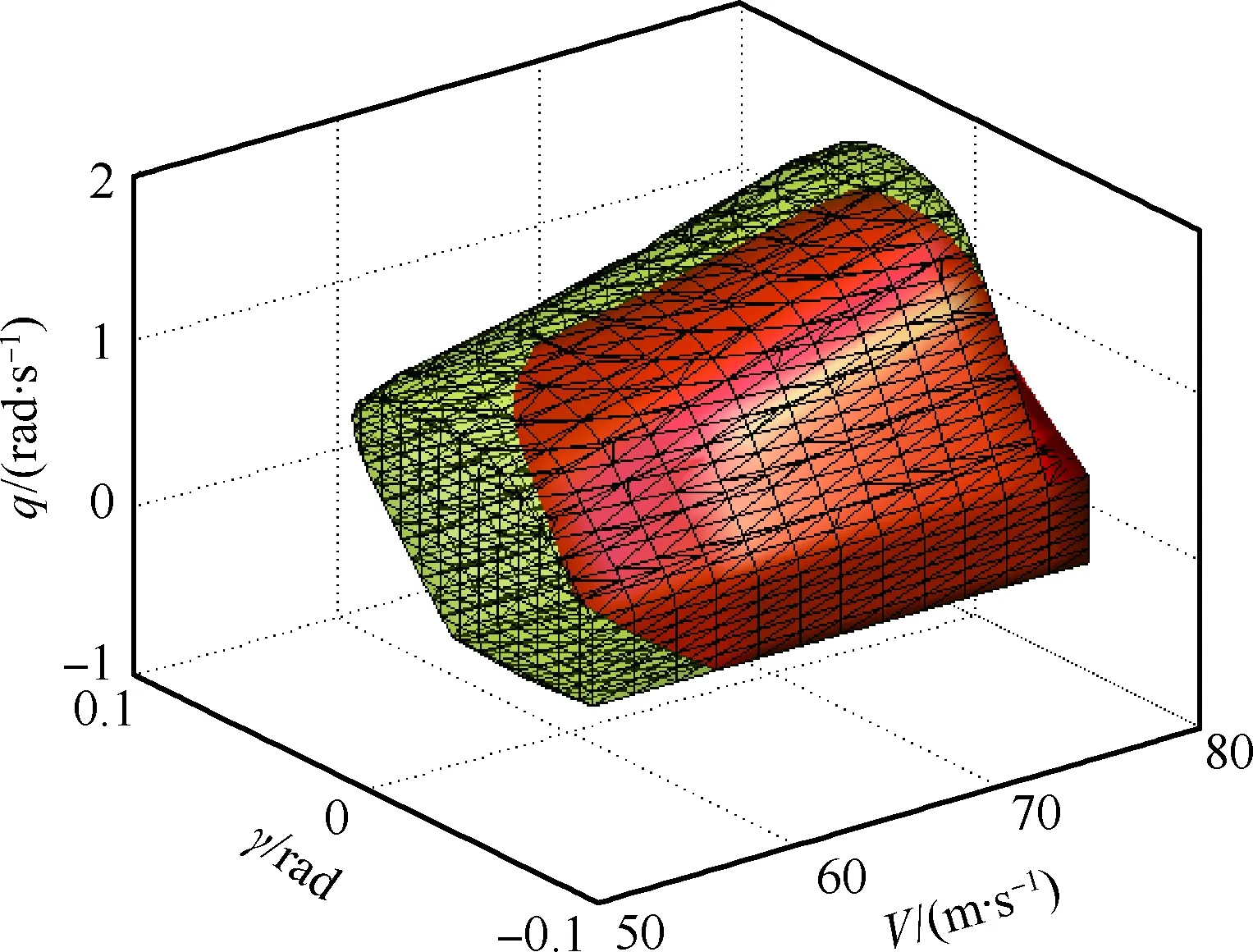
图3 不结冰与结冰程度为0.1时的可达集对比Fig.3 Comparison of reachability sets between no ice and icing degree at 0.1

图4 结冰程度为0.1和0.2时的可达集对比Fig.4 Comparison of reachability sets between icing degree at 0.1 and 0.2

飞行在安全包线内可以保证安全飞行，可达集计算的范围可以表征飞行包线的范围。驾驶员的操纵和外界瞬时扰动使飞机状态的变动在这一范围内时，飞机可以通过操纵使其安全着陆。

4 基于可达集的飞机结冰风险评估

第3节中的可达集是基于四维动力学方程计算的，根据动力学方程，可以将速度与航迹倾角随时间的变化率提取出来进行计算[16]，不考虑俯仰角速度和迎角对飞行风险影响，分析飞机结冰飞行风险，将方程取为二维的动力学方程计算可达集。

本节将二维可达集作为安全评估的标准，分析不同结冰程度时的风险概率[17-18]。由于结冰飞行试验风险很大，因此一般的风险评估使用地面模拟飞行的数据，在此基础上分析风险概率。

由第3节着陆安全可达集分析可知，着陆时，飞机的安全稳定状态应该处于速度、航迹倾角的合理范围内，因此将飞行状态超出可达集范围作为危险发生的判据。速度大于或小于可达集限制认为飞机可能发生危险，航迹倾角超出给定范围认为飞机将发生危险。用概率表达式表示为[19]

Pd=1

VVmax，γ<γminorγ>γmax

(11)

式中：Pd为发生危险的概率。

4.1 参数提取介绍与极值理论

为计算飞机结冰条件下的飞行风险概率，首先设定初始飞行状态：初始飞行的高度为100 m，速度为80 m/s，航迹倾角为-3°。将驾驶员操纵模型作为系统的输入，进行蒙特卡罗仿真，得到多组仿真结果。驾驶员操纵模型根据文献[20]所提供的模型确定，其模型可以表示为

(12)

式中：x0为操纵量初始值；σ为模型参数；u(x-x0)为单位阶跃函数。

根据统计学和概率论的知识可知，仿真次数越多，即得到的样本容量越大，统计结果越接近真实情况，因此仿真次数需要足够多。同时，为减少计算机的计算任务量，本文取1 000次仿真结果进行分析。

飞行风险可以通过关键飞行参数超出其边界值的概率来进行评估[21-22]，在着陆阶段，飞行状态是关键飞行参数，当飞行状态超出安全包线时，可认为飞行风险事件发生。飞行风险是小概率事件(事件发生概率<10-9)，很难通过计算所有发生事件次数除以总的仿真次数来得到风险事件发生的概率。而此类事件一旦发生就会带来严重危害，例如金融风险、巨额保险的赔付、重大的自然灾害、重大人为事故等。

极值理论在计算这种低频高危风险事件的概率方面具有其特有的优势[23-24]。极值理论认为，在不需要知道独立同分布随机变量的累积概率分布条件下，就可以得到极值的分布函数，这是因为随着样本容量的增加，极值的分布渐近地趋于一个确定的分布函数。

如果存在常数序列{an>0}和bn，使得当n→∞时：

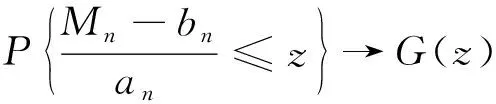
(13)

式中：ξ为非退化分布函数，那么G必属于广义极值(Generalized Extreme Value，GEV)分布族，即

(14)

式中：-∞<μ<∞，σ>0，-∞<ξ<∞。

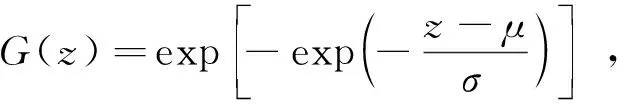
当ξ>0时，G(z)表示Fréchet分布。

当ξ<0时，G(z)表示Weibull分布。

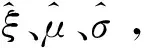
4.2 风险概率计算

将飞机质点动力学方程降维成二维方程，仅对速度和航迹倾角进行可达集的求解，可以得到飞机的速度和航迹倾角的安全范围。将这一范围作为飞机风险评估的判据，状态超出安全范围认为飞机将发生危险。在计算风险概率时，风险的定义是飞机失控，即接地之前或者接地瞬间飞机失去控制，不包括飞机可控状态下飞机着陆后冲出跑道或者飞机结构受损。因此不将飞机速度较大并且不适合着陆的情况定义为风险，仅考虑航迹倾角或速度超过最小限制的情形。

不结冰时得到的可达集结果如图5所示。根据结果，航迹倾角或速度的较小极值在红色虚线以内，红色虚线所在直线为

γ+0.018 9V=0.727 4

(15)

安全包线所在区域应该满足以下条件:

(16)

为计算风险概率，定义变量d，其值为

d=-(γ+0.018 9V)

(17)

基于提取的参数，本文对根据速度V和航迹倾角γ的参数极值计算所得的变量d进行参数辨识，分别可以得到变量d的极值分布GEV模型。其中对于变量d来说，μd=-1.608 3，σd=0.042 5。概率计算方程可表示为

(18)

由式(18)计算可得，干净外形条件下，d=-0.727 4，飞行风险概率是

P=1-G(d)=9.962 1×10-10

(19)

结冰程度为0.1时，所得到的可达集结果如图6所示。根据结果，仍然将航迹倾角或速度的较小极值限制在红色虚线以内，红色虚线所在

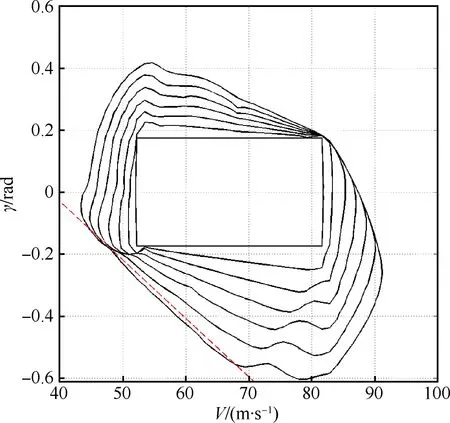
图5 结冰程度为0时的安全包线Fig.5 Safety envelope when icing degree is 0

直线为

γ+0.018 9V=0.854 6

(20)

安全包线所在区域应该满足以下条件：

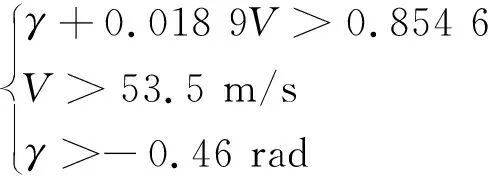
(21)

结冰程度为0.1时，气动力和气动特性发生改变，安全包线收缩，飞行状态超出可控范围的可能性大大提高，风险概率增大，此时d=-0.854 6，根据Gumbel模型计算此时的风险概率为

P=1-G(d)=1.986 9×10-8

(22)

结冰程度为0.2时,所得可达集结果如图7所示。根据上述计算过程，航迹倾角或速度的较小极值限制在红色虚线以内，红色虚线所在直线为

γ+0.018 9V=0.985 2

(23)

安全包线所在区域应该满足以下条件：

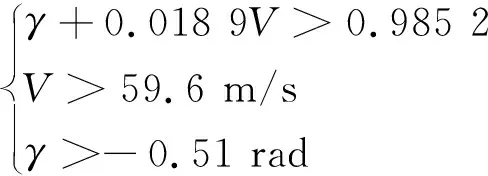
(24)

当结冰程度为0.2时，由于气动特性改变进一步加剧，安全包线进一步收缩，此时d=-0.985 2，风险概率由概率模型计算：

P=1-G(d)=4.292 7×10-7

(25)

当风险概率小于10-8时，认为结冰严重程度属于“极小的”范畴，可认为飞机不会发生风险。当风险概率范围为10-8≤P<10-6时，驾驶人员应当立即开启除冰装置。当风险概率为P≥10-6时，驾驶员应当立即改变飞行路线，使飞机驶离结冰区。当速度或航迹倾角大于限制值时，驾驶员不应继续着陆，应当改出着陆阶段，调整状态后重新进行着陆。

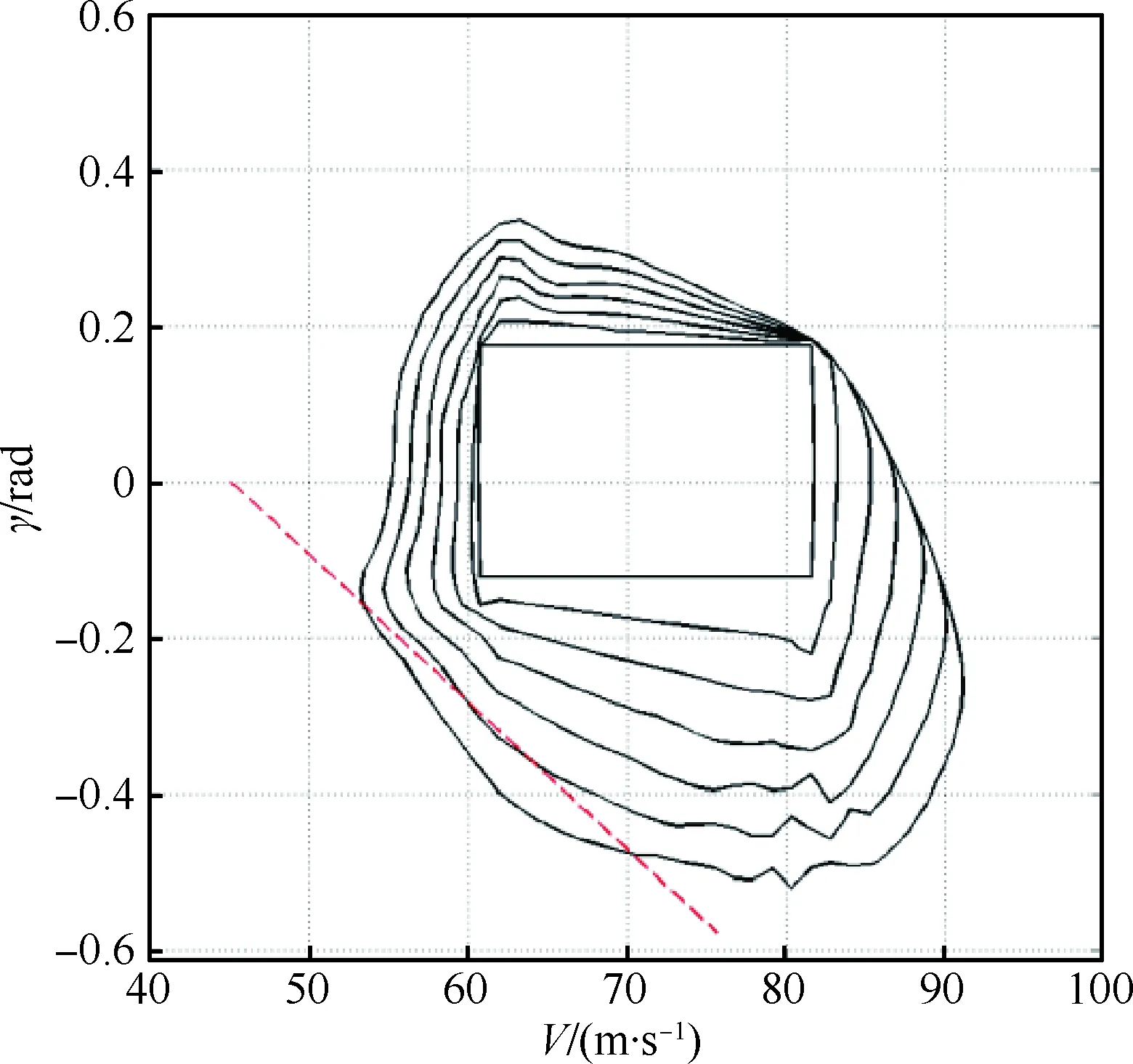
图6 结冰程度为0.1时的安全包线Fig.6 Safety envelope when icing degree is 0.1

平尾涉及俯仰舵面的操纵，一旦结冰，飞机纵向的俯仰操纵将受到影响。根据文献[25]的研究，平尾结冰相对于机翼结冰来说，对飞机的纵向升力和阻力产生的影响较小。因此在相同程度的结冰条件下，平尾结冰对应的反向可达集结果范围比机翼结冰对应的可达集范围更大。仿真结果如图8所示，结冰程度同为0.1时，相比于机翼结冰，平尾结冰对应的可达集结果在低速区域和负航迹倾角区域范围更大，而在高速区域范围有略微的收缩，这与实际情况相对应[26]。

图7 结冰程度为0.2时的安全包线Fig.7 Safety envelope when icing degree is 0.2

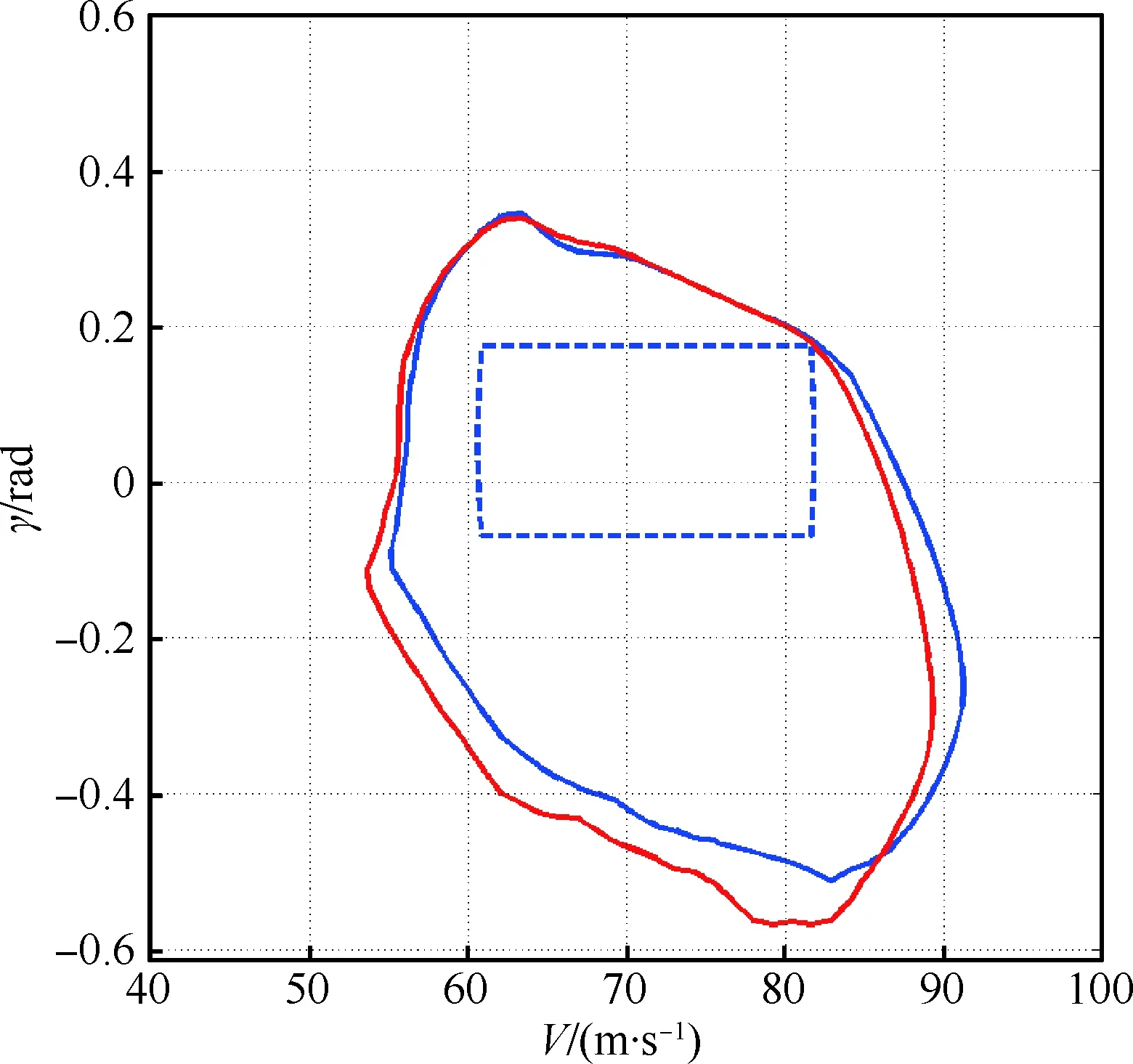
图8 平尾结冰与机翼结冰对应的安全包线Fig.8 Safety envelopes when tailplane icing and wing icing

5 结 论

基于可达集理论，以结冰条件下的飞机质点动力学模型为分析对象，利用可达集方法对其着陆阶段的安全包线进行求解，根据安全包线和极值理论计算不同结冰程度下的着陆风险概率，并对驾驶员操纵提出指导，主要结论如下：

1) 可达集适合用于计算飞机飞行的安全包线，计算结果直观可视。结冰飞机着陆时使用可达集计算安全包线能够指导驾驶员安全着陆，飞机状态一旦偏离可达集，驾驶员应该立即改变飞机的操纵，改出着陆阶段，避免发生恶劣后果。

2) 随着结冰程度的加剧，飞行的可达集范围缩小，稳定裕度降低，更容易发生危险。其主要原因是飞机结冰后的各项气动导数发生了较大变化，动力学特性变差，操纵难度增加，导致飞机的稳定性降低，风险系数增加。

3) 以可达集为安全包线的结冰飞行风险评估方法，能够得到飞机超出结冰后安全包线的风险概率，该方法能够用来定量地计算不同结冰程度下的飞行风险，能够指导驾驶员进行合理的操纵，从而规避危险。

水平集方法可求解出飞机着陆的安全包线，风险评估方法结合可达集计算结果能评估出飞机结冰后的飞行风险。然而着陆过程中飞行风险涉及的因素有很多，本文利用可达集计算时采用的模型为简化的模型，所计算的结果仍然需要进一步的研究才能更加准确。后续将增加飞机系统维数，建立更加准确的仿真框架和模型，并对仿真模型进行有效验证。