基于有限元及试验的发动机飞轮模态分析

孟德健，张伯俊，董晓伟

（1.天津职业技术师范大学机械工程学院，天津 300222；2.天津职业技术师范大学汽车与交通学院，天津 300222）

随着汽车工业的迅猛发展，汽车舒适性已成为当前行业研究的重点之一。发动机的振动与噪声是研究的一个重要方面，飞轮是发动机重要组成部分，对其结构、动态属性的研究分析具有一定的意义[1-2]。本文利用模态函数指示法和多参考点最小二乘复频域法对测量得到的汽车发动机飞轮频响函数矩阵进行模态参数估计，通过二级验证区分汽车飞轮的真实模态和虚假模态并识别密集模态和重根模态，将试验仪器测得的固有频率和振型与理论计算所得进行对比，验证飞轮模型的正确性。

1 飞轮的有限元（ANSYS）模态分析

1.1 ANSYS分析过程

ANSYS软件是由美国ANSYS公司研制的，该软件能较好地迎合分析需求，而ANSYS Workbench正是为了组件的重新组合而设置的一个专用平台，因此增加了ANSYS产品的易用性和开发性[3]。

ANSYS Workbench能够与多数CAD软件相连接，如 Pro-E、UG、CATIA、Solidworks等现代设计中应用较广的高级CAD软件，实现了数据的共享和交换。ANSYS Workbench分析的基本过程如图1所示。

图1 ANSYS Workbench分析的基本过程

1.2 建立有限元模型

应用Solidworks软件建立发动机飞轮的三维模型，如图2所示。打开ANSYS Workbench软件，定义材料属性弹性模量为1.38×105MPa，泊松比为0.156，密度为7.28×10-6kg/mm3，将此模型转入Design Modeler平台，进入Modal界面选用Automatic方式进行网格划分，得到20 928个节点，11 655个单元，如图3所示。

图2 三维模型

图3 网格划分

1.3 有限元模态分析

在汽车飞轮有限元模型边界处不施加任何约束使其处于自由状态，理论计算得到前6阶刚体模态[4]。为获取汽车飞轮的弹性模态参数，在“Max Modes to Find”中填写12，得到前6阶弹性模态，发动机飞轮固有频率如表1所示，振型如图4所示。

表1 模态固有频率

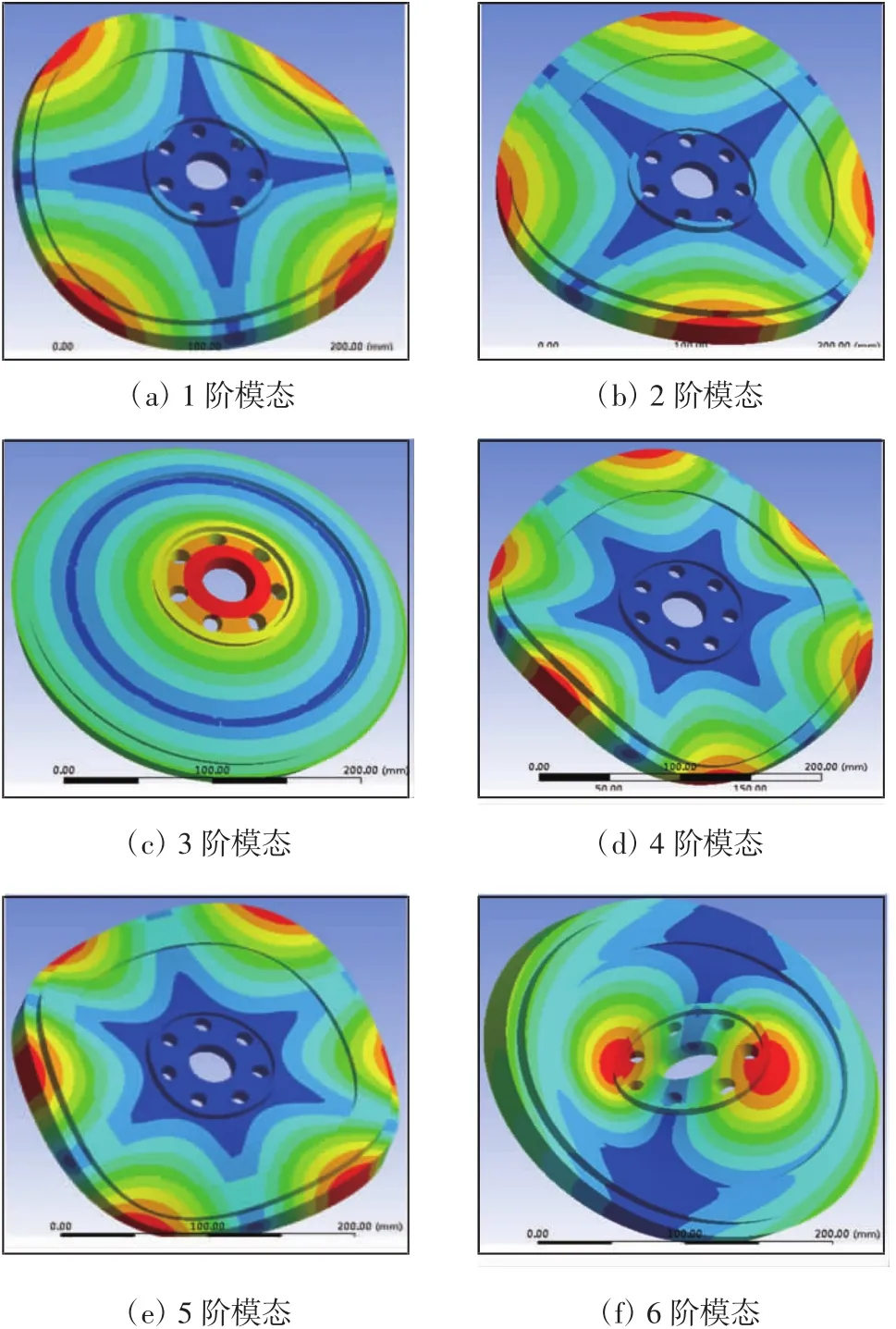
图4 振型图

观察固有频率与振型，理论计算软件得到的3阶模态与6阶模态为真实模态。1阶模态与2阶模态、4阶模态与5阶模态固有频率都很接近。从图4可知，1阶振型与2阶振型相似，4阶振型与5阶振型相似，这极有可能是密集模态或重根模态。采用试验模态分析可验证上述推论。

2 飞轮的模态试验分析

2.1 试验方法及测试系统组成

采用多参考点锤击技术对飞轮进行动态性能测试[5-6]。在数据预采集时，选择模态参考点。由于飞轮是对称结构，故不能选择对称的两驱动点作为参考点。对比多个驱动点的测量数据,选择峰值多且易于观察的驱动点为第1个模态参考点。在选择第2个模态参考点时，参考点的峰值应不同于第1个模态参考点的峰值，这样才能通过2个参考点测出更多的共振峰[7]。设置带宽和谱线数保证在采样时间结束前响应时域信号能被全部获取,实现无泄漏测量。在数据采集过程中，通过观察功率谱曲线、频响函数幅频特性曲线和相干函数曲线保证采集数据准确可靠，测试系统组成如图5所示。

图5 测试系统组成

2.2 测点布置与激振方案

根据飞轮的外观情况进行简化，将其默认为一个平面，不计厚度和表面的孔。对同一个驱动点敲击3次，最终接收数据为3次数据的平均值。

2.3 互易性检查

互易性检查的目的是验证该飞轮是否符合试验要求。试验方法是以测点12作为参考点时，激励测点10得出响应曲线；以测点10作为参考点时，激励测点12得出响应曲线。互易性越好，测试的数据越可靠，互易性检测如图6所示。

图6 互易性检测

2.4 频响函数曲线图

频响函数曲线图如图7所示。用复模态指示函数法和多参考点最小二乘复频域法计算试验模态。

图7 频响函数曲线图

2.5 BroBand和NarBand模态参数估计方法分析

2.5.1 BroBand方法

BroBand方法是一种对系统极点、模态振型进行整体估计的多自由度方法。识别出的模态固有频率如表2所示，对应的多参考点最小二乘复频域法分析所得各阶振型如图8所示，置信度MAC值如表3所示。

表2 BroBand方法模态固有频率

观察发现，识别出的3阶模态和6阶模态振型图是独立的，与本身相比模态的置信度高，与其他相比模态置信度很低，所以为真实模态。1阶模态与2阶模态的频率接近，二者的振型图均为内部对称2点间的上下振动，置信度列表显示二者之间的置信度很低，因此可能为密集模态或重根模态。4阶与5阶模态的固有频率也接近，二者的振型图均为边缘的扭转振动，二者之间的置信度很低，所以可能为密集模态或重根模态。再通过复模态指示函数法分析试验数据，进一步确定是否为密集模态或重根模态。

2.5.2 NarBand复模态指示函数法

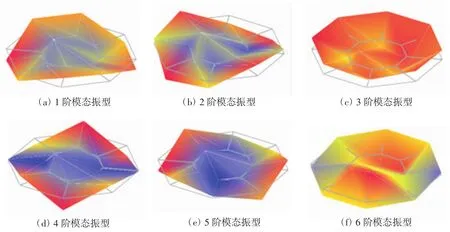
图8 多参考点最小二乘复频域法分析所得各阶振型

表3 BroBand方法置信度MAC值

NarBand方法基于频率分辨率来估计系统阻尼，然后得出有关模态振型，进而计算出系统模型的极点，对模态进行比例换算，模态固有频率如表4所示，模态指示函数法分析所得各阶模态振型如图9所示，置信度MAC值如表5所示。

通过上述方法分析得出，3阶模态的振型图是独立的，表5显示与其他模态置信度相比很低，所以其为真实模态。1阶模态与2阶模态的频率接近，二者振型图为对称2点间的上下振动。4阶与5阶模态的频率接近，振型图均为边缘弯曲振动。6阶模态与7阶模态的频率接近，振型图为内部的扭转振动。对比MAC值，发现第1阶模态与第2阶模态的置信度很高，确认二者为重根模态。分析4阶与5阶模态为密集模态或重根模态，进行二级验证。

表4 NarBand方法模态固有频率

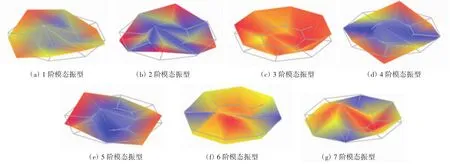
图9 模态指示函数法分析所得各阶模态振型

表5 NarBand方法置信度MAC值

2.6 CROSS-MAC（2种估计之间的MAC值比较）

通过数学方法模态判定准则对2种方法估计的结果分别进行不同模态的MAC值比较和不同估计之间的MAC值比较，从而分析得出真实模态，MAC值比较如表6所示。2种估计方法的1阶模态的相似度为92.2%、3阶模态的相似度为99.0%、4阶模态的相似度为99.8%、5阶模态的相似度为92.0%和6阶模态的相似度为98.1%，但是2阶模态的相似度极低为10.1%。综上所述，前2阶模态属于重根模态，4阶和5阶模态属于密集模态。

表6 MAC值比较

3 有限元法和试验模态的对比分析

3.1 振型比较

将通过试验仪器测得的振型与理论计算软件得出的振型进行比较，振型比较如图10所示。由图10可知，1阶振型图是边缘2个对称点之间的弯曲振动，3阶振型图是中间部分的垂直上下弯曲振动，4阶振型图与5阶振型图是飞轮边缘的弯曲振动，6阶振型图是飞轮内部的扭转振动。

图10 振型比较

3.2 固有频率比较

试验仪器测得固有频率与理论计算得出的固有频率误差如表7所示。由表7知，频率最小误差为0.20%，最大误差为6.68%。各阶理论模态值与试验模态值误差在10%以内，根据工程实践经验知误差值在标准

（）（）规定的范围内[8]。这说明所建立的发动机飞轮有限元模型能够较为准确地描述发动机飞轮的振动特性。

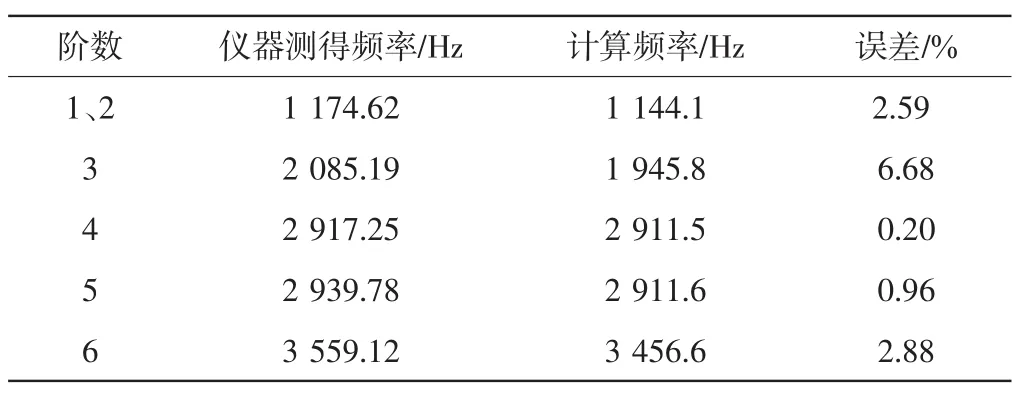
表7 试验与理论频率误差

4 结语

本文利用复模态指示函数法和多参考点最小二乘复频域法对测量所得汽车发动机飞轮频响函数矩阵进行分析，然后再对结果进行了二级验证。运用OROS V3动态信号分析仪、NVGATE和Modal II分析软件，采用多参考点锤击技术对飞轮进行动态性能测试，获得试验模态参数。利用Solidworks与ANSYS软件建立飞轮模型并计算出了理论模态参数。结果显示，二者的固有频率接近、振型相似，验证了发动机飞轮模型的准确性。本研究对改进发动机飞轮结构，促使汽车轻量化具有一定的参考价值。