剪纸艺术在几何教学中的应用
孙章财


摘 要:学生有一种喜欢用“思维的眼光,实际操作,实现自我价值”把握事实的需要,教师应当满足这种需要。通过动手操作能消除呆板枯燥,有利于从具体材料中进行抽象、思考、推论,得出结论,还能在保护好学习信心的同时激发学生对知识和事实新的兴趣。
关键词:归纳总结;思维能力;体验感
一、背景
剪纸艺术是最古老的中国民间艺术之一,它能给人以视觉上透空的感觉和艺术享受。剪纸是用剪刀将纸剪成各种各样的图案,如窗花、门笺、墙花、顶棚花、灯花等。每逢过节或新婚喜庆,人们便将美丽鲜艳的剪纸贴在家中窗户、墙壁、门和灯笼上,节日的气氛也因此被烘托得更加热烈。剪纸艺术,通过一把剪刀、一张纸,就可以表达对生活的热爱。但大家不知道的是剪纸艺术还可以运用到数学几何教学中,下面我们就来具体阐述一下。
中学数学教学大纲明确指出:初中数学教学的目的是使学生掌握初中几何的基本知识以及应用这些知识解决有关几何计算和有关几何作图的基本技能;培养与发展学生由实践到理论、由具体到抽象以及进行推理论证的逻辑思维能力;培养与发展学生的观察、想象与表达几何形象的空间想象能力,进一步培养运算能力,发展逻辑思维能力和空间观念。教学大纲还特别指出:发展学生的思维能力是培养学生各项能力的核心。由此可见,发展学生的思维能力在整个中学数学教学中占有非常重要的地位。
知识技能要求让学生经历探究物体与图形的形状、大小、位置关系和變换的过程,掌握空间与图形的基础知识和基本技能,并能解决简单的问题。数学思考要求:经历运用数学符号和图形描述现实世界的过程,建立初步的数感和符号感,发展抽象思维;丰富对现实空间及图形的认识,建立初步的空间观念,发展形象思维;经历观察、实验、猜想、证明等数学活动过程,发展合情推理能力和初步的演绎推理能力,能有条理地、清晰地阐述自己的观点。
解决问题要求初步学会从教学的角度提出问题、理解问题,并能综合运用所学知识和技能解决问题,发展运用意识;形成解决问题的一些基本策略,体验解决问题策略的多样性,发展实践能力与创新精神;学会与人合作,并能与他人交流思维的过程和结果。
情感与态度要求:能积极参与数学学习活动,对数学有好奇心与求知欲;在数学学习活动中获得成功的体验,锻炼克服困难的意志,建立自信心;初步认识数学与人类生活的密切联系及对人类历史发展的作用,体验数学活动中包含的探索性与创造性,感受数学的严谨性以及数学结论的确定性;形成实事求是的态度以及进行质疑和独立思考的习惯。
透过剪纸可以呈现数学思维的发展过程,体验理论的形成来源于实际操作,让数学抽样变为可观察、可验证的实际活动。克服传统的板演填鸭式方式,将教学与手工操作、验证、学生参与、知识体验结合在一起,使课堂活动化、情趣化、操作化,大大提高了学生的参与度。透过剪纸将空洞的理论变为现实体验,变为可碰触的实践操作和可展示的过程,加深学生的体验感和成功的喜悦。使知识逻辑发展转变为可操作、具体化、细节化的活动过程。活动中学生的参与感、合作感、融入感,获得感将得到最大限度的满足,同时也将获得成功的满足感,求知欲和数学情趣将得到提高。
二、剪纸艺术在教学中的应用
剪纸与教学结合,课堂活动化案例做如下展示,敬请参考:
教具准备:草稿纸、小剪刀、圆规、直尺三角板。
案例一:角的认识、角大小比较、互余互补关系。
准备在草稿纸上画下30度、45度、60度、90度、135度的角各两个并把它们剪下来。同时体会角的大小与开口大小有关与角的边长无关。
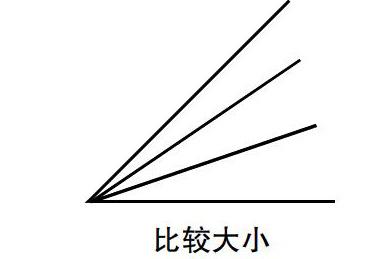
1.角的大小比较
将30度角、分别与45度角、60度角进行比较,比较方法将角的顶点及一条边重合比较大小。
2.互余互补关系
将30度角与60度角拼到一起与90度角比较大小;将两个45度角拼在一起与90度角比较大小。这样在实际操作中归纳得出互余的关系。
将135度角与45度角拼在一起,将两个90度角拼在一起组成两个180度角进行对比归纳得出互补的关系。
案例二:圆、圆心角、圆周角、圆心角与圆周角关系。教具准备:草稿纸、圆规、尺子。
1.在草稿纸上画两个半径为10厘米的圆,将它们剪下来比较放在一起比较大小。归纳得出同圆、等圆的概念。
2.画一个半径为10厘米的圆,用圆规在圆上找两条相等的弧并分别连接两条弧的端点成弦,再将个弧的端点与圆心相连形成角,同时归纳说明圆心角概念。
将其中一条弧及其圆心角组成的扇形剪下来,放到另一个扇形上进行比较观察重合的情况。得出结论:在同圆(等圆)中相等的弧所对的弦、圆心角相等。
3.画一个半径为10厘米的圆,用圆规在圆上找一条弧并分别连接弧的端点成弦,再将这条弧的端点与圆上的第三点相连形成角,同时归纳得出圆周角的概念。另在圆上取一点画出同弧所对的圆周角,将其中一个圆周角剪下来放到另一个圆周角上比较大小,观察重合的情况。归纳得出结论:同圆(等圆)中相等的弧弦所对的圆周角相等。
4.画一个半径为10厘米的圆,取一段弧画出同弧所对的圆心角、圆周角并把它们都剪下来,将圆心角对折后与圆周角对比观察大小重合情况。得出结论:同圆(等圆)中同弧所对的圆周角是圆心角的一半。
案例三:三角形内角和与三角形外交和(多边形内角和)。
在草稿纸上画一个三角形,将它的三个角剪下来放到一起形成180度。同样也可以画出三角形的一个外角,验证三角形的一个外角等于与它不相邻的两个内角之和。
案例四:三角形全等的判定方法(SSS、SAS、ASA、AAS、HL)每个方法都可以。教具准备:圆规、直尺、小剪子、草稿纸。
1.三边对应相等的三角形全等
在草稿纸上任意画一个自己喜爱的三角形,教师在黑板上板板演带领学生用尺规作出一个与原三角形三边对应相等的三角形,并将它剪下来与原三角形对比形状大小是否完全重合。归纳得出结论:三边对应相等的三角形全等。AB=A1B1、BC=B1C1、AC=A1C1。
2.两边及其夹角对应相等的三角形全等
在草稿纸上任意画一个自己喜爱的三角形,教师在黑板上板板演带领学生用尺规作出一个与原三角形有一个内角相等及对应角的两边也对应相等的三角形,并将它剪下来与原三角形对比形状大小是否完全重合。归纳得出结论:两边及其夹角对应相等的三角形全等。AC=A1C1、∠A=∠A1=a、AB=A1B1。
其余判定方法可以类比上述进行操作。
作图过程中,教师注意巡视观察,学生的作图情况并作出适当的板演,确保能正常完成作图。
马克思主义认为,教育起源于生产劳动。教育就是从这种生产劳动的实际需要中产生的。这种观念认为教育起源于人类在劳动过程中形成的超生物经验的传递与交流。其目的在于借助抽象思维和语言,促进个体人的形成,动手操作是几何图形的初衷,许多的证明判定都可以用剪纸方法来进行验证。
课堂上,只要让每个学生体验到取得成功的个人的、人格上的欢乐,那么这种课就不会把教师弄得心情焦躁、筋疲力尽。学生的精力都被纳入了正确的轨道。因为他们的全部注意力都集中在如何更好地完成剪纸对比归纳上。动手操作不仅是一些实际技能和技巧,而且也是一种智力发展,是一种思维和语言的素养。
参考文献:
[1]孙宏安.中学数学教学法新编[M].华中师范大学出版社,2007.
[2]罗明东,褚远辉.教育学当代教育一般性问题概论[M].高等教育出版社,2006.
编辑 温雪莲

