衰落信道中（15，7）循环码性能分析

刘 洋，李正权

（江南大学，江苏 无锡 214122）

循环码是重要的线性分组码，在多个领域广泛应用[1]。循环码具有两个基本特点：一是编码电路与译码电路非常简单，易于实现；二是代数性质好，译码方法成熟。循环码的编码和译码实现简单，且检错、纠错能力强。它不但可以检测随机的错误，还可以检测突发的错误[2]。（n，k）循环码可以检测长为n-k或更短的任何突发错误，包括首尾相接突发错误。

循环码又称格雷码（Gray Code），是一种无权码，其编排特点是相邻两个数码之间符合卡诺图中的邻接条件，即相邻两个数码之间只有一位码元不同，码元就是组成数码的单元。循环码的优点是没有瞬时错误，适用于数字通信系统。本文主要针对（15，7）循环码，研究其编译码过程，并分析其在高斯信道下的编码性能。

一、循环码原理

（一）（15，7）循环码生成多项式

循环码所有码字均可由生成多项式生成。（n，k）循环码中，生成多项式次数为n-k，且为xn+1的因子。xn+1除以生成多项式后的多项式称为校验多项式[3-4]。（15，7）循环码的生成多项式为 g（x）=x8+x7+x6+x4+1

（二）（15，7）循环码生成矩阵

当g（x）升幂排列时，生成矩阵G为：

对G进行初等变换，即可求得生成矩阵（k行k列的k阶单位矩阵）：

（三）（15，7）循环码校验矩阵

校验多项式为 h（x）=x7+x6+x4+1。G=[I P]，Q=PT，则校验矩阵为H=[Q I]。

对H进行初等变换，即可求得校验矩阵（r行r列的r阶单位矩阵）：

二、循环码编码

针对（n，k）循环码，生成多项式 g（x）和信息码多项式 m（x），m（x）=mk-1xk-1+mk-2xk-2+…m1x+m0。用 xn-k乘以 m（x），得到的 xn-km（x）的次数必定小于n；用g（x）除xn-km（x），得到余式r（x），其次数小于n-k；将r（x）加到信息位之后作为监督位，即将r（x）和 xn-km（x）相加得到码多项式 c（x）=xn-km（x）+r（x）=mk-1xk-1+mk-2xk-2+…m1x+m0+rn-k-1xn-k-1+...。 因此，（15，7）系统循环码的编码步骤包括三步：第一步，将信息码 m（x）乘以 xn-k变成 xn-km（x）k；第二步，用 xn-km（x）除以 g（x），得商 q（x）和余式 r（x）；第三步，将 xn-km（x）加上余式 r（x），确定码字多项式 c（x）。（15，7）循环编码过程如图1所示。

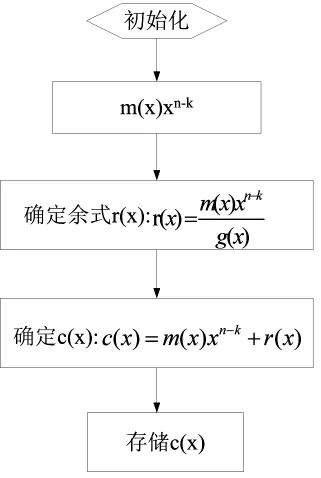
图1 （15，7）循环码编码过程流程图

三、循环码译码

接收端译码有两个要求：检错和纠错。循环码的发送码字与接收码字间存在如下关系式：

式（5）中 C（x）为发送码字，R（x）为接收码字，E（x）为错误图样。当E（x）=0时说明接收没有错误，用 g（x）去除 R（x），即除以 C（x），由于 C（x）是g（x）生成的，故 C（x）必能为 g（x）除尽，显然 R（x）与 E（x）同余式 R（x）≡E（x）mod g（x），以 g（x）除E（x）所得余式称为伴随式 S（x）。利用 R（x）、E（x）、S（x）可实现译码和纠错，具体步骤为：第一步，用接收码字 R（x）除以 g（x），如果除尽则无错，否则有错；第二步，由余式 S（x）找出对应图样 E（x）；第三步，将 E（x）与 R（x）作模 2 加，得发送码字C（x），从而实现纠错目的。系统循环码的译码方法如图2所示。

图2 （15，7）循环码译码过程流程图

四、仿真结果

本文利用 matlab 软件[5-6]，实现（15，7）循环码编译码。假设输入信息码为0 1 1 1 1 0 0，则编码前波形如图3所示。编码后信息波形如图4所示。

图3 编码前信息波形

图4 编码后信息波形

经过高斯信道传输后的波形如图5所示信噪比假设为10dB）。

由图5可知，即使在信噪比较好的条件下，经过信道传输，信息波形还会有一定程度失真，此时需要循环码对信息进行译码并对其纠错、检错。

图5 信道传输后信息波形

图6 译码后信息波形

由图6可知，虽然传输信道造成信息波形在一定程度上失真，但经过循环码译码纠错后，能够恢复出原信息波形。在此基础上，本文研究（15，7）循环码在不同衰落信道中的性能。首先研究（15，7）循环码在高斯信道下的性能，如图7所示。

由图7可见，循环码在信噪比较好（6dB以上）时的高斯信道下，能带来一定的性能增益。但在信噪比较低时的高斯信道环境中，由于纠、检错能力的限制，循环码性能增益减小。

其次，本文进一步研究（15，7）循环码在瑞利衰落信道中的性能，如图8所示。比较图7与图8可以发现，信道的衰落会造成传输系统的性能显著下降，而循环码一定程度上可以抑制信道的衰落。

图7 不同信噪比的高斯信道中循环码性能

图8 不同信噪比的瑞利信道中循环码性能

最后，本文研究（15，7）循环码在更一般、衰落程度较小的Nakagami（m参数设为5）信道中的性能，如图9所示。结果表明，循环码在衰落程度较小的信道中，也可以提供较大的性能增益。

图9 不同信噪比的Nakagami信道中循环码性能

五、结语

本文利用Matlab，实现了（15，7）循环码编译码。在此基础上，进一步研究了不同信道环境下（15，7）循环码的性能，为循环码在系统设计中的应用提供理论依据。