几何条件的组合与转化
——一道习题解法之深度理解
●
(温岭中学,浙江 温岭 317500)
《普通高中数学课程标准(2017版)》(以下简称《新课标》)指出:平面解析几何通过建立直角坐标系,借助直线、圆与圆锥曲线的几何特征,导出相应的方程,用代数的方法研究它们的几何性质,体现形与数的结合;再运用代数方法进一步认识圆锥曲线的性质以及它们的位置关系,运用平面解析几何方法解决简单的数学问题和实际问题,感悟平面解析几何中蕴含的数学思想[1].
为了突出“用代数的方法解决几何问题”这一数学思想,一线的教师们也煞费苦心.编制或选择一些代数运算量较大的问题,于是“计算量大”就成了解析几何的另一个代名词,也成为许多学生学不好解析几何的借口.解析几何之难真的在“计算量大”上吗?
1 问题
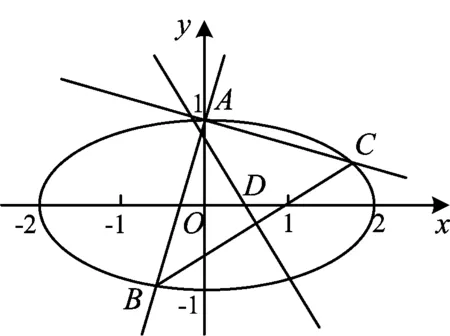
图1
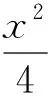
学生解法1片段设直线AB的方程为y=kx+1,与椭圆方程x2+4y2=4联立可得
x2+4(kx+1)2=4,
从而

从而BC的中点为



学生的疑惑:该解题思路很常规,为什么运算量如此之大?两个极大值f(k1)与f(k2)之中哪个为最大值呢?
学生解法2设B(x1,y1),C(x2,y2),BC的直线方程为y=kx+b,与椭圆方程x2+4y2=4联立可得
(1+4k2)x2+8kbx+4b2-4=0,
从而
Δ=16(4k2+1-b2).
因为AB⊥AC,所以
x1x2+(y1-1)(y2-1)=0,


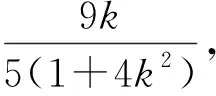

2 问题的完善
上述解答中,如此繁复的计算学生都能无误,说明该学生的运算能力比较强.那么解法1能不能解决问题呢?
解法1补充因为k1k2=-1,k3k4=-1,从几何角度看
f(k1)=f(k2),f(k3)=f(k4).
由k1,k2,k3,k4是方程4k4-33k2+4=0的根,知
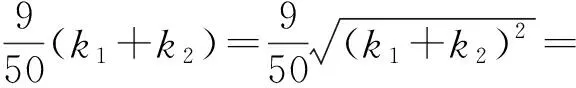

3 反思
解题时我们应该有这样的意识:没有任何一个题目是彻底完成的,总还会有些事情可以做,如果对问题进行充分地研究和洞察,就可以将解题的方法加以改进,从而深化对问题的理解.
3.1 命题者的意图
上述两种解法的运算量有着天差地别,解法1虽然常规,但计算量如此之大,显然不是命题者的意图.众所周知,解析几何是用代数的方法解决几何问题,因此首先要将几何条件代数化,然后才是代数运算.也就是说,转化是前提,运算是基础.解析几何问题不仅考查运算求解能力,还要考查转化化归能力.
3.2 不同解法的本质原因

3.3 常见几何对象
纵观浙江省近几年的解析几何高考题,考查的几何对象有:1)位置关系类,2017年和2018年考查了直线垂直,2015年考查了线段平分,2012年和2015年考查了对称问题,2016年考查了曲线相交,2014年考查了直线与曲线相切,2011年考查了特殊的三点共圆;2)度量关系类,2017年考查了线段长度问题,2012年、2013年、2015年和2018年考查了三角形面积问题.因此掌握不同几何对象的代数转化是必要的,这是运算的前提.
图2
3.4 几何条件代数化的特点

(2017年浙江省数学高考理科试题第21题改编)
1)几何条件代数化的多样性.
目标|PA|·|PQ|需要转化为坐标表示.若借助两点间距离公式
则|PA|·|PQ|的表示就需要知道点P,Q,A的坐标;若将公式等价变形为
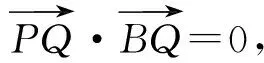
分析1为了目标和已知的统一性,可选择长度的代数化方式为
垂直的代数化方式是两条直线的斜率为负倒数.


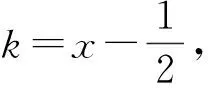
|PA|·|PQ|=-(k-1)(k+1)3.
令f(x)=(1+x)3(1-x),其中-1 f′(x)=(1+x)2(2-4x), 分析2若BQ⊥PQ的代数化形式为 |PB|2=|BQ|2+|PQ|2, 则|BQ|的代数表示为点B到直线AP的距离,|PB|为两点距离. |PQ|2= |PB|2-|BQ|2= |PA|2=(k2+1)(k+1)2, 从而 |PA|·|PQ|=(1-k)(k+1)3. 下同解法1. 2)几何条件代数化的可组性. 几何条件的代数转化并不一定是孤立地将每个条件转化,也可以将相关的几何条件进行组合转化,通常结合的条件越多,转化越巧妙,计算越简单,不同的组合方式也会得到不同的解答方法. 分析3因为点A,P,Q在同一条直线上,即∠APQ=180°,所以 知道点P,Q,A的坐标就可以求解. (1+k)3(k-1), 于是 |PA|·|PQ|=(1+k3)(1-k). 下同解法1. 分析4解法3最大的运算量就是求交点Q的坐标,结合点Q为垂足的特点,转化为与之相邻的点P,B的坐标,就较为简单,因此可转化为 从而简化运算. 解法4设P(x,x2),则 f′(x)=-4x3+3x+1=-(x-1)(2x+1)2, 故 图3 如图3,取AB的中点M,则 而直线AB的方程为 即 4x-4y+3=0, 下同解法4. |PA|·|PQ|= 下同解法4. 从上面的解法3~6中可以发现,不同的代数化方法是解析几何一题多解的根源,也是解析几何繁复多变的根源.因此掌握几何条件代数化的方法就是掌握解析几何解题的命脉. 再次回味《新课标》中关于解析几何的两句话:1)用代数的方法研究它们的几何性质,体现形与数的结合,因此需要将几何条件转化为代数条件,然后用代数的方法进行研究,最后将代数结果转化为几何条件,这就是解析几何问题解决的三步曲:转化—运算—转化;2)运用平面解析几何方法解决简单的数学问题和实际问题,感悟平面解析几何中蕴含的数学思想,体会数学思想是教学的目的,因此大计算量并不是《新课标》的本意,教师与学生无需为大运算量花费大量的时间与精力,“如何转化、怎么巧妙转化”是研究的重点.

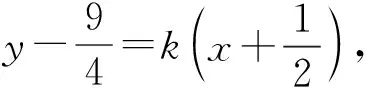
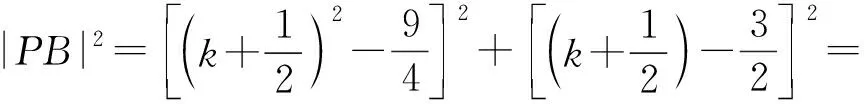

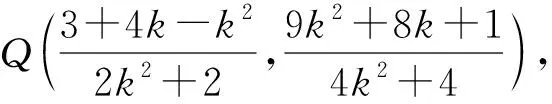
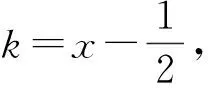
















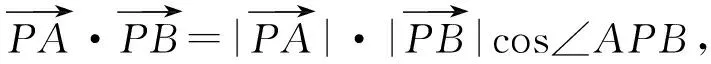


4 结束语

