函数问题中“隐”极值范围的求解策略
●●
(泉州外国语中学,福建 泉州 362000) (泉州第五中学,福建 泉州 362000)
函数导数的试题,往往需要以导数为工具研究函数的极值、最值情况,而结合“隐”极值范围的探索使得试题的难度大大增加.如何有效求解此类问题?笔者基于近几年高考、模拟考试题的研究,探索这类问题的解法并总结规律,得到其模式化解题策略.
1 函数的“隐”极值问题
1.1 函数极值的判定
一般地,设函数f(x)的导函数为f′(x),若x0满足f′(x0)=0,且在x0两侧附近f′(x)的函数值异号,则x0是f(x)的极值点.若f′(x)在x0两侧附近满足“左正右负”,则x0是f(x)的极大值点,f(x0)是极大值;若f′(x)在x0两侧附近满足“左负右正”,则x0是f(x)的极小值点,f(x0)是极小值.
1.2 函数的“隐”极值
在研究函数f(x)极值的过程中,若导函数y=f′(x)的“变号零点”确定存在,但无法确定其具体值,我们把此类问题称为函数的“隐”极值问题.
正可谓“只在此山中,云深不知处”!如何寻找“隐”极值的取值范围呢?
2 “隐”极值问题的求解策略
2.1 不含参数的“隐”极值问题的求解策略——整体替换,超越化有理
一般地,不含参数的“隐”极值问题的解题程序为:
1)由函数零点存在定理,确定“隐”极值点所在的大致范围;
2)结合等式f′(x0)=0,通过整体替换,化超越式为有理式,从而把“隐”极值f(x0)表达成有理式;
3)应用函数知识,确定所得有理式的大致范围.
由此得到的“隐”极值的范围是不够精确的,相对比较粗糙,因此,命题者在命制此类问题时,设问方式基本以证明题的形式呈现,要求证明所给出的“隐”极值的取值范围.解题者只需要根据题目要求的范围精度,适度调整“隐”极值点所在的范围,即可实现对“隐”极值的限制.
例1已知函数f(x)=ax2-ax-xlnx,且f(x)≥0.
1)求a;
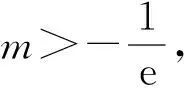
2)证明:f(x)存在唯一的极大值点x0,且e-2 (2017年全国数学高考卷Ⅱ理科试题第21题) 1)a=1(过程略). 2)证明由a=1得f(x)=x2-x-xlnx,从而 f′(x)=2(x-1)-lnx(其中x>0), 令g(x)=f′(x),则 由f′(x0)=0,得 2(x0-1)-lnx0=0, 即 lnx0=2x0-2, 综上可得e-2 评注第2)小题有两个难点有待解决:1)估计极值点x0的范围;2)由极值点x0的范围,确定f(x0)的范围.这两个难点的破解,直接关系到解题的成败.难点1)的破解策略:根据零点存在定理估计极值点x0的范围,并根据难点2)的需要及时调整该范围;难点2)的破解策略:函数极值f(x0)的式子中含有x0的超越式,通常利用f′(x0)=0消去超越式,化成只含x0的有理式,然后估计该有理式的取值范围. 例2已知函数f(x)=ex-ln(x+m). 1)设x=0是f(x)的极值点,求m的值并讨论f(x)的单调性; 2)当m≤2时,证明:f(x)>0. (2013年全国数学高考卷Ⅱ理科试题第21题) 1)m=1.函数f(x)的单调递减区间为(-1,0),单调递增区间为(0,+∞). 2)证明当m≤2时, f(x)=ex-ln(x+m)≥ex-ln(x+2). 从而存在x0∈(-1,0),使g′(x0)=0,当-2 g(x0)=ex0-ln(x0+2). 即 ln(x0+2)=-x0, 评注第2)小题的证明可分成两个步骤: 1)更换主元,得 h(m)=ex-ln(x+m)(其中m≤2), 其最小值为h(2)=ex-ln(x+2), 故只需证明h(2)=ex-ln(x+2)>0对x>-2恒成立. 2)求g(x)的“隐”极小值g(x0)的范围,g(x0)为含x0的超越式,仍然是利用g′(x0)=0消去超越式,化成只含x0的有理式解决. 一般地,含参数的“隐”极值问题的解题程序: 1)由函数零点存在定理,并结合参数a的取值范围,确定“隐”极值点x0所在的区间,并保证“隐”极值点x0能取遍区间内的每一个值; 2)结合等式f′(x0)=0,得a与x0的关系式,通过代入消元,从而把“隐”极值f(x0)表达为只含x0或a的一元函数; 3)应用函数知识,确定所得一元函数的值域. 由此得到的“隐”极值的范围是准确的.因此,命题者在命制此类问题时,设问方式可以是求解“隐”极值的取值范围,也可以要求证明所提供的范围.解题者需要根据参数的取值范围,确定“隐”极值点所在的精确范围,从而得到“隐”极值f(x0)的取值范围. 例3已知函数f(x)=2xex+m(x2+2x). (2018年福建省数学适应性练习2理科试题第21题) g(x0)=(2x0-4)ex0+m(x0+2)2. 由g′(x0)=0,得 从而 h′(x)=-(x2+x+1)ex<0, 从而h(x)单调递减,于是 h(1) 又h(0)=-2,h(1)=-2e,故-2e 评注第2)小题把极小值点x0代入得到最小值g(x0),其中g(x0)是既含有x0的超越式,又含有参数m的二元式.求解g(x0)的取值范围有两个难点:1)运用消元思想,通过代换把g(x0)转化为一元式;2)通过观察范围,结合函数单调性,准确求出所留下的未知数的取值范围x0.解决上述两个难点后,即可通过构造函数,利用导数求出g(x0)的取值范围. (2016年全国数学高考卷Ⅱ理科试题第21题) 因为f(0)=-1,所以当x>0时,f(x)>f(0),即 故(x-2)ex+x+2>0成立. 2)当x>0且a∈[0,1)时, f(0)+a=-1+a<0,f(2)+a=a≥0. 因为y=f(x)+a在区间(-2,+∞)上单调递增,所以存在x0∈(0,2],使g′(x0)=0,且当0 由g′(x0)=0,得 a=-f(x0), 即 因此 评注第2)小题需结合第1)小题的结论,得到“隐”最小值g(x0),后续在求解g(x0)的取值范围时,其解题策略与例3如出一辙,不再赘述. 函数“隐”极值点问题的探究及其解题策略,其意境深远,真可谓:只在此山中,云深不知处;不懈艰难寻,豁然穿迷雾!

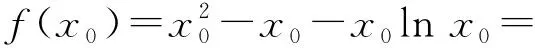



2.2 含参数的“隐”极值问题的求解策略——灵活消元,二元化一元

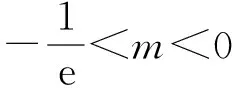




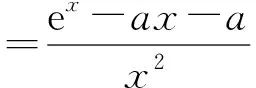
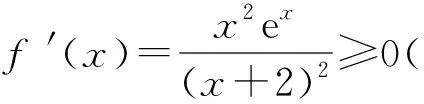


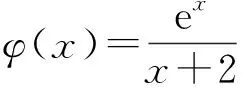
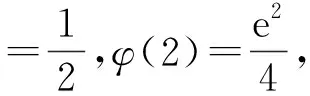

3 结束语

