基于多对称虚拟变换的二维波达方向估计算法*

聂卫科， 徐楷杰， 牛进平， 周 延， 冯大政

(1.西北大学 信息科学与技术学院，陕西 西安 710127； 2.西安电子科技大学 机电工程学院，陕西 西安 710071；3.西安电子科技大学 雷达信号处理国家重点实验室，陕西 西安 710071)

0 引 言

传感器阵列信号处理是雷达、声纳、移动通信等领域的关键技术[1～3]。高分辨二维波达方向估计利用传感器阵列接收数据，估计目标的方位角和俯仰角，相比一维估计，可提取更多的空间信息[4]，提高信号分选和目标识别概率[5]。多信号分类(multiple signal classification,MUSIC)算法[6]作为子空间类高分辨算法的经典代表，需要二维谱峰穷尽搜索和参数配对过程，运算量庞大。随后提出的ESPRIT算法[7]无需谱峰搜索,直接得到参数估计的闭式解，显著地减少了运算量。然而，ESPRIT算法受限于阵列子阵结构，无法直接应用于自身无平移不变结构的阵列。针对此问题，虚拟内插方法[8]和高阶累积量技术[9]对阵列进行不同的扩展，从新的角度构造旋转不变因子，从而进行ESPRIT算法，同样得到了闭式解。文献[10]中，Friedlander B等人将不具备旋转不变性的任意结构传感器阵列，通过虚拟内插方法，变换成另一个等距均匀线阵，再寻求等距均匀线阵的旋转不变结构，实现了任意阵列波达方向的闭式解。基于虚拟内插实现ESPRIT算法，可将任意阵列变换一个或几个与自身结构完全一样，只是位置上有相对平移的虚拟阵列，利用真实阵列与虚拟阵列间的旋转不变性实现信号波达方向的求解。虚拟内插变换技术还可应用于宽带信号处理，前后向平滑算法，以及求根MUSIC中[11]。虚拟内插类算法以其独特的优势而备受关注，兴起了传感器信号处理研究的新热点。

本文提出了一种多对称虚拟变换二维波达方向估计算法，该算法通过对任意阵列进行多对称虚拟变换，基于虚实子阵构造一种特殊的旋转不变因子矩阵，利用该旋转不变因子矩阵进行信号源俯仰角的求解，再基于该俯仰角进行方位角的搜索。估计的方位角和俯仰角可自动配对，由于充分利用了多个虚拟阵列的累加接收数据，平滑了接收数据中的正负项误差，抑制了虚拟变换矩阵导致的样本数据偏差，显著提高了二维波达方向的估计精度，仿真实验证实了本文算法的有效性。

1 传感器阵列和信号模型

假设P个远场窄带非相关信号源sp(t)(p=1,2,…,P)入射到如图1所示的空间任意部署的M(M≥P)个各向同性的传感器阵元组成的阵列A0上。

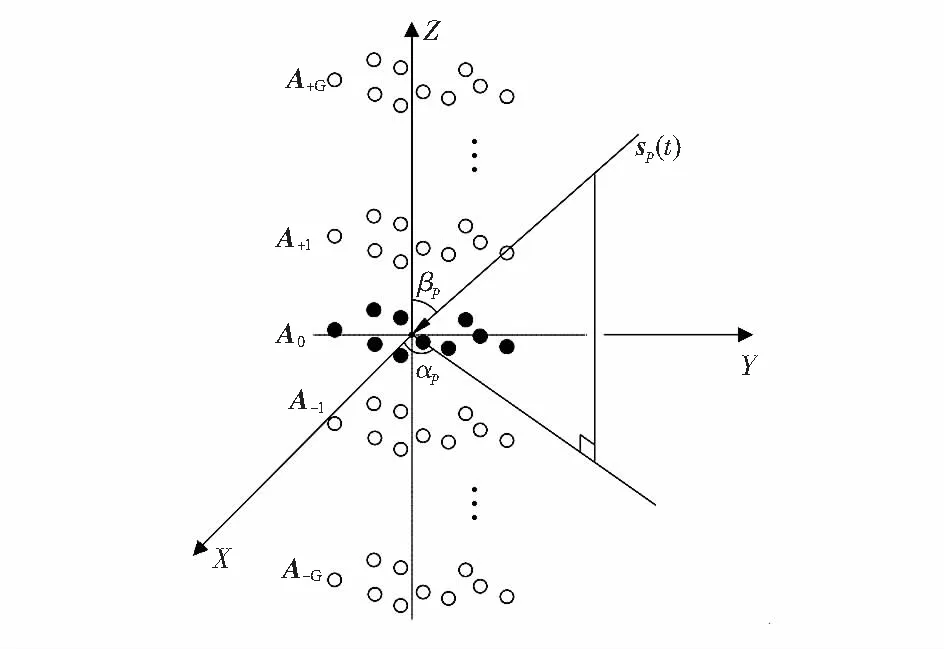
图1 传感器阵列结构

设第m个阵元的位置坐标为(xm,ym,zm)(m=1,2,…,M),选坐标原点为参考点，那么阵列在t时刻对应的输出信号为

(1)

式中n(t)为阵列的加性白Gauss噪声矢量,且

s(t)=[s1(t),s2(t),…,sP(t)]T

(2)

A=[a(α1,β1),a(α2,β2),…，a(αP,βP)]

(3)

a(αp,βp)=[a1p(αp,βp),a2p(αp,βp),…,

aMP(αp,βp)]T

(4)

amp(αp,βp)=e-j(2π/λ)Δ

(5)

Δ=xmcosαpsinβp+ymsinαpsinβp+zmcosαp

(6)

式中αp和βp分别为第p个入射波信号的方位角和俯仰角，λ为信号波长。

2 本文算法原理

设待估信号源位于某一个观察区域内，该观察区域定义为Θ，设该Θ区域的俯仰角的左右边界分别为θβl和θβr，方位角的左右边界分别为θαl和θαr；对该观察区域的俯仰角和方位角均以步长为Δθ进行划分

Θβ=[θβl,θβl+Δθ,θβl+2Δθ,…,θβr-Δθ,θβr]

(7)

Θα=[θαl,θαl+Δθ,θαl+2Δθ,…,θαr-Δθ,θαr]

(8)

则对该观测区域，阵列θαl的阵列流行矩阵为

Af=[a(θαl,θβl),a(θαl+hΔθ,θβl+kΔθ),a(θαr,θβr)]

(9)

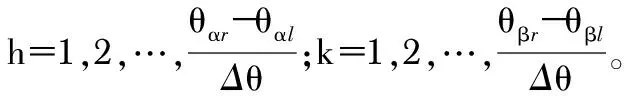
设存在关于阵列A0所在平面对称的G组阵列A-1-A+1,A-2-A+2,…,A-g-A+g,…,A-G-A+G，第g(g=1,2,…,G)组对称阵列中第m个阵元的坐标分别为P+gm(xm,ym,zm+dg)，P-gm(xm,ym,zm-dg)，则第g组对称阵列对观察区域Θ内的阵列流型矩阵为

A+g=[a+g(θαl,θβl),a+g(θαl+hΔθ,θβl+kΔθ),

a+g(θαr,θβr)]

(10)

A-g=[a-g(θαl,θβl),a-g(θαl+hΔθ,θβl+kΔθ),

a-g(θαr,θβr)]

(11)

这样，阵列A0的阵列流型矩阵Af与第g组对称阵列对区域Θ内的阵列流型矩阵之间存在对应的变换关系为

(12)

对Af进行奇异值分解Af=U[Σ,0][V1V2]H,从而得到变换关系为

(13)

利用以上变换关系可由阵列A0在t时刻输出信号进行第g组对称阵列在该时刻虚拟输出变换

(14)

再由阵列之间的相对位置关系，可知

Ag=A-GΦg+G,g=-1,-2,…,G

(15)

Φ=diag(e-j2π/λdcos β1,e-j2π/λdcos β2,…,e-j2π/λdcos βp)

(16)

令

XΣ=X-G+X-G+1+…+Xg+…+XG-κ

(17)

XΓ=(X-G+X-G+1+…+X-G+κ-1)-

(XG+XG-1+…+XG-κ+1)

(18)

XΣ和XΓ列堆栈得到

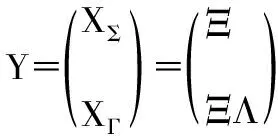
(19)

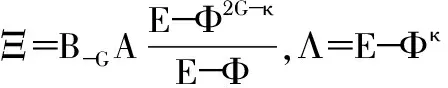
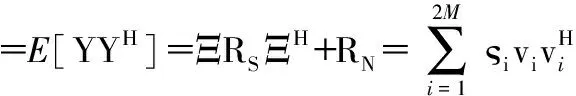
(20)

(21)

式中span为矩阵的列张成，有且只有[12]唯一的非奇异矩阵T，使得下式成立

(22)

根据空间相对理论[13]有

span{US1}=span{Ξ}=span{US2}

(23)

再由式(19)两子阵的阵列流型的关系，可得到两子阵的信号子空间的关系

US2=Ξ(TT-1)ΛT=US1T-1ΛT=US1Ψ

(24)

由于信号互不相关，必有Λ=TΨT-1。

因此，Ψ的特征值与Λ的对角元素相等，T的列就是Ψ的特征向量，只要求得Ψ，就可以由式(16)求得信号的俯仰角βp。可求得Ψ的最小二乘法(LS)解ΨLS为

(25)

对ΨLS进行特征分解，也即获得矩阵Λ的对角元素值，从而可以反解信号源的俯仰角βp，进而把解出的俯仰角βp代入阵列A0的阵列模型,即可通过一维MUSIC搜索获得方位角的估计αp

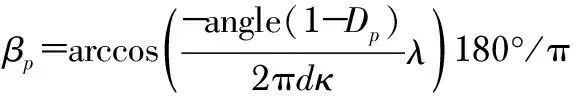
(26)

式中Dp(p=1,2,…，P)为ΨLS特征值，angle为取复角主值。

3 仿真实验

为验证本文所提算法的性能，考虑空间任意传感器如图1所示，阵元数为M=10，G=5的任意阵列，各阵元坐标为(-0.33,0.1)，(-0.13,0.18,0)，(0.12,0.175,0)，(0.33,0.1,0)，(0,0.35,0)，(-0.2,0.07,0)，(0.2,-0.07,0)，(0,-0.22,0)，(-0.2,-0.28,0)，(0.2,-0.28,0)。远场窄带信号源(俯仰角，方位角)为(20°,45°)；变换扇区：俯仰角5°～25°，方位角35°～55°，步长均为1°。

实验一不同信噪比和快拍下二维波达方向估计均方根误差对比。

快拍数分别取400和1024，信噪比取-5～15 dB，各阵元噪声为零均值白复高斯噪声，图2为1 000次独立实验下，本文算法与文献[10]算法的二维波达方向估计均方根误差对比仿真结果。

由图2可以看出，两种算法对信号源俯仰角及方位角估计的均方根误差均随信噪比及快拍的增大而降低，在相同快拍下本文算法优于文献[10]算法。如图2(a)所示，在对俯仰角进行估计低信噪比下，本文算法无论高快拍或是低快拍时，具有明显的优势，且本文算法低快拍下的估计误差比文献[10]算法高快拍的估计误差还要小；在基于俯仰角对方位角进行一维MUSIC搜索时，如图2(b)所示，两种算法均是基于俯仰角一维搜索方位角，在相同的快拍数下，本文算法俯仰角和方位角的均方根误差均小于文献[10]算法。

实验二不同信噪比和快拍下二维波达方向估计成功率对比。

快拍数分别取400和1 024，信噪比取-5～15 dB，各阵元噪声为零均值白复高斯噪声，以下为1 000次独立实验本文算法与文献[10]算法的二维波达方向估计成功率对比仿真结果。

可以看出，两种算法对信号源二维波达方向估计的成功率均随信噪比及快拍的增大而增加，在相同条件下本文算法优于文献[10]算法。如图3(a)所示，在对俯仰角进行估计中，信噪比为5 dB时本文算法成功率已达100 %，此时，文献[10]方法在400和1 024快拍下，具有约78 %和96 %的成功概率。如图3(b)所示，基于俯仰角对方位角进行一维MUSIC搜索时，由于本文算法估计的俯仰角精度更高，因此,基于此搜索得到的方位角精度也高于文献[10]的方法，因而成功概率也更高。综合图3可知，在高低两种快拍场景下，本文算法在-5～15 dB的大动态范围内均具有较高的估计成功概率。

4 结 论

提出一种多对称虚拟变换的二维波达方向估计算法。该算法通过构造实阵列的多个虚拟平移子阵列，利用多个虚拟阵列的累加数据进行列堆栈，并结合空间相等理论，推导出一种新的虚实旋转不变因子，求得信源俯仰角的闭式解。通过获得的俯仰角，将二维搜索转换为一维搜索，得到对应方位角的估计，明显降低了经典二维MUSIC算法的搜索复杂性。由于采用了多个虚拟阵列的累加数据，显著抵消了虚拟变换矩阵带来的数据误差，提高了估计精度。仿真实验在大范围的信噪比场景下，对低、高不同快拍的应用情况，进行了估计精度的均方根误差统计，和成功概率性能比较，结果表明了本文算法的有效性。