探索“三角形全等判定的ASS”成立的条件

摘 要:在线段及角是否相等的判断方法中,全等三角形的判定十分常用。判定三角形是否全等的方法包含“SSS(边边边)”“SAS(边角边)”“AAS(角角边)”及“ASA(角边角)”等四种,而在判定直角三角形是否全等时,还包含“HL(斜边、直角边)”。众所周知,在对两个三角形是否全等进行判定时,无法将“ASS(角边边)”作为条件,但是对于为什么却不甚了解。实质上,“ASS”也可用于三角形全等的判定中,但是并非是任意三角形都能适用,有一定限制条件存在。对此,本文就三角形全等判定中的“ASS”条件展开探究。
关键词:全等三角形;判定依据;ASS
初中数学教材中,“全等三角形”属于核心概念,而在该单元的拓展内容中,便涉及了“角边边能否判定三角形全等?”学习该内容之前,学生已对三角形关于边、高、内角、中线及角平分线等相关概念有所了解,依托“尺规作图”进行三角形的绘制,帮助学生将三角形全等的四种判定方法掌握,然而对于三角形全等判定中“ASS”为什么不能采用,却不具备深刻的理解,缘由不明了。因此,探究三角形全等判定中是否能够采用“ASS”,总结出“三角形全等判定的ASS”成立与不成立条件,能够帮助学生深刻理解“ASS”是否能够对三角形全等进行判定,拓展学生的知识储备,活跃学生的思维能力。
一、 探索“三角形全等判定的ASS”成立的必要性
众所周知,三角形三边分别对应相等的两个三角形是全等的,即为“SSS(边边边)”,而相应的也有“SAS(边角边)”“AAS(角角边)”及“ASA(角边角)”,皆可用于两个三角形是否全等的判定中。但是,当有两边及其一边对角分别对应相等的两个三角形,却并不一定就是全等的,由于没有简称的缘故,因此教材中也未出现“ASS(角边边)”。
笔者经过调查后发现,关于“ASS(角边边)”的理解与应用方面,初中教师与学生都有一定偏差存在。数学这门学科具有严密逻辑思维,在学生初次接触简单严密的逻辑思维训练时,教师不能出现漏洞,以免学生严密逻辑思维能力的培养受到影响。因此,教师就必须对教材中的说法准确理解,也就是有两边及其一边对角分别对应相等的两个三角形,却并不一定就是全等的。此处的“不一定就是全等的”,表明有个别是全等,也有个别不是全等的,教师切忌一律采用“一定不全等”的说法来概括,需要深入探索“ASS(角边边)”的不同情况,同时展开具体分析,在面对“ASS(角边边)”对两个三角形是否全等进行判定时,还需融入其他方法。
二、 “三角形全等判定的ASS”成立条件的探究
根据浙教版八上第一章1.5的三角形全等判定的学习,学生通过给定条件下画三角形。分别画出“两边长确定,夹角已知”或者“三条边长度确定”或者“两个内角确定夹边长固定”的三角形,同学们画出了唯一的形状和大小,通过互相对比发现能够叠合,从而体验了:“图形確定就能判定全等”。因此,在同学们纷纷猜想“为什么就没有ASS定理”的时候,我们就可以,运用这种体验,帮助学生找到“ASS”不成立的原因及成立时的条件特征。
(一) 分析“ASS”不成立的原因
根据上述体验,若给定条件下,图形不能确定。即:某条边或者角在满足条件下,依然可以活动。则可以找到“ASS”不成立的原因。
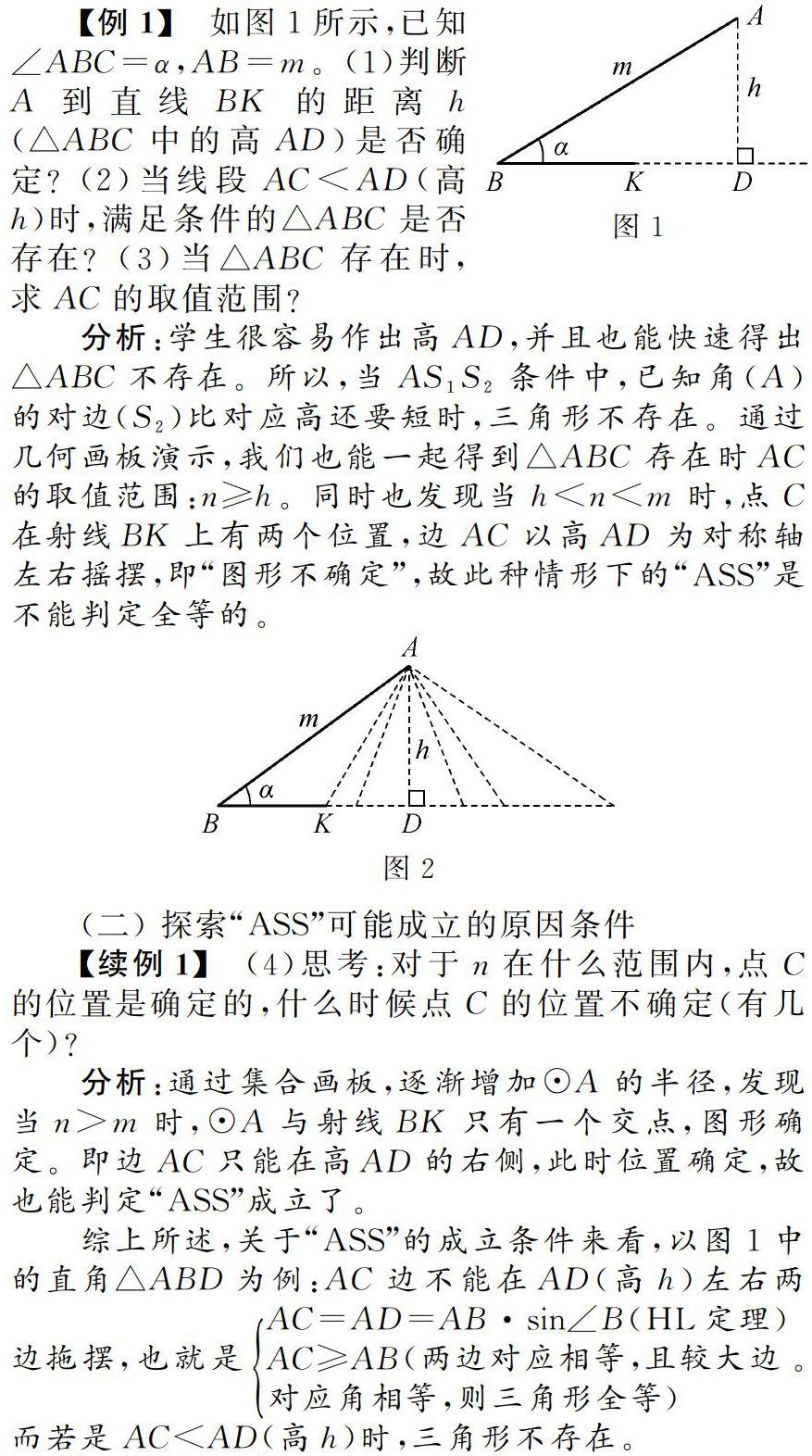
【例1】 如图1所示,已知∠ABC=α,AB=m。(1)判断A到直线BK的距离h(△ABC中的高AD)是否确定?(2)当线段AC 分析:学生很容易作出高AD,并且也能快速得出△ABC不存在。所以,当AS1S2条件中,已知角(A)的对边(S2)比对应高还要短时,三角形不存在。通过几何画板演示,我们也能一起得到△ABC存在时AC的取值范围:n≥h。同时也发现当h<n<m时,点C在射线BK上有两个位置,边AC以高AD为对称轴左右摇摆,即“图形不确定”,故此种情形下的“ASS”是不能判定全等的。 (二) 探索“ASS”可能成立的原因条件 【续例1】 (4)思考:对于n在什么范围内,点C的位置是确定的,什么时候点C的位置不确定(有几个)? 分析:通过集合画板,逐渐增加⊙A的半径,发现当n>m时,⊙A与射线BK只有一个交点,图形确定。即边AC只能在高AD的右侧,此时位置确定,故也能判定“ASS”成立了。 综上所述,关于“ASS”的成立条件来看,以图1中的直角△ABD为例:AC边不能在AD(高h)左右两边拖摆,也就是AC=AD=AB·sin∠B(HL定理)AC≥AB(两边对应相等,且较大边对应角相等,则三角形全等)。而若是AC 三、 探索“ASS”成立的条件的证明 数学课堂教学中,教师于备课过程中,尽管会立足于“知识与技能”“过程与方法”及“情感态度与价值观”三个维度的数学课程目标进行教学目标的设计,然而具体教学中却往往仅对“知识与技能”目标予以了重视。翻阅了大量与“ASS”相关的资料后,笔者发现多数教师皆将“ASS”能对三角形全等进行判定的特殊条件当作教学的主要目标,也就是“有两边及较大边对应角相等的两个是全等的,是三角形全等中‘ASS判定的特殊条件。”以数学语言表述转化该结论,可通过下述四种情况进行划分: (一) 满足“ASS”的三角形是否一定全等 【例2】 图3所示等腰△ABC中,AB=AC,点D是BC边上除B、C之外的任意一点,判定△ABD是否全等于△ACD。 分析:通过“几何画板”的运用,将D点选定并拖动,通过在BC边上移动之后,得到△ABD与△ACD。△ABD的边AB和AD与△ACD的边AC和AD相等,且∠B=∠C,但是一般情况下这两个三角形是一个为锐角、一个为钝角三角形的缘故,因此两个三角形并非一定是全等的。所以,两个三角形即便满足“ASS(角边边)”也并非一定全等。
(二) 满足“ASS”的直角三角形是否全等
下图中,继续移动点D至AD⊥BC时,ABD与△ACD成了直角三角形,由图4、图5至图6进行动态演示。此时“ASS”中的角可以是移动点D后获得的直角,所以“ASS”就转化成了“HL”。如此不难发现,“ASS”中,“HL”是一种特殊情形。
(三) 满足“ASS”的锐角三角形是否全等
【例3】 如上图6所示,△ABC和△A′B′C′为锐角三角形,其中AB=A′B′、AC=A′C′、∠B=∠B′,求证:△ABC≌△A′B′C′。
分析:过点A、A′分别作AD⊥BC于点D、A′D′⊥B′C′于点D′,结合“AAS”即可将△ABD≌△A′B′D′证实,得到AD=A′D′,此时再结合“HL”即可将直角△ADC≌直角△A′D′C′证实,因此∠C=∠C′,从而可将△ABC≌△A′B′C′证实。
结合上述探究能够总结出“两个锐角三角形,若是两边及其中一边对角对应相等,即为全等”,也就是说在两个锐角三角形是否全等的判定中,可采用“ASS”。
(四) 满足“ASS”的钝角三角形是否全等
【例4】 如图7所示,△ABC和△DEF为钝角三角形,AB=DE、AC=DF、∠C=∠F,求证:△ABC≌△DEF。
分析:在钝角△ABC与钝角△DEF全等的证明中,在元素对应相等的基础上,也需要依据,可以根据“SSS”将BC=EF证明,也可以根据“AAS”将∠B=∠E证明。总体来说就是将另一对边或对角相等证明。
方法1:证明BC=EF
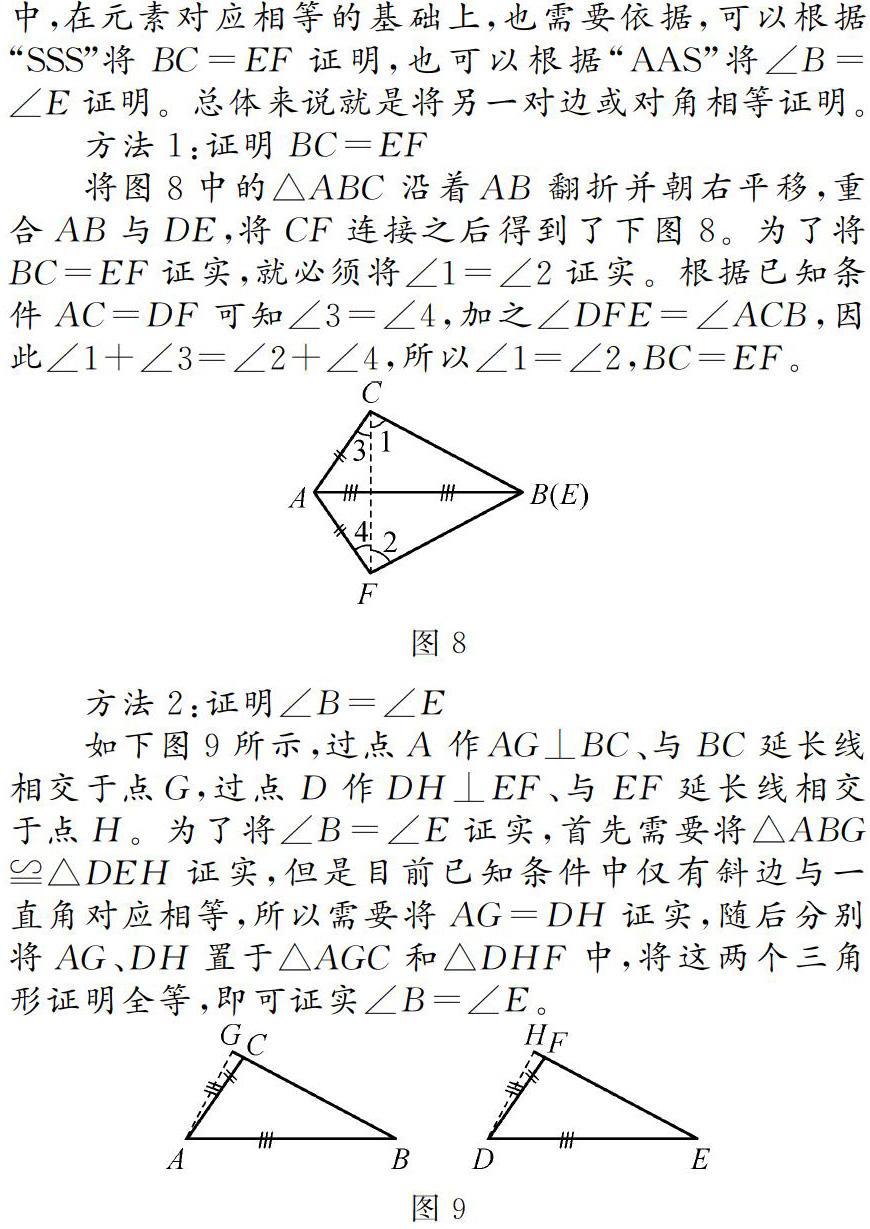
将图8中的△ABC沿着AB翻折并朝右平移,重合AB与DE,将CF连接之后得到了下图8。为了将BC=EF证实,就必须将∠1=∠2证实。根据已知条件AC=DF可知∠3=∠4,加之∠DFE=∠ACB,因此∠1+∠3=∠2+∠4,所以∠1=∠2,BC=EF。
方法2:证明∠B=∠E
如下图9所示,过点A作AG⊥BC、与BC延长线相交于点G,过点D作DH⊥EF、与EF延长线相交于点H。为了将∠B=∠E证实,首先需要将△ABG≌△DEH证实,但是目前已知条件中仅有斜边与一直角对应相等,所以需要将AG=DH证实,随后分别将AG、DH置于△AGC和△DHF中,将这两个三角形证明全等,即可证实∠B=∠E。
四、 结论
结合上述分析得知,个别特定条件下,通过“ASS(角边边)”能够将两个三角形全等证实,因此总结出“有两边及较大边对应角分别对应相等的两個三角形是全等”。然而,需要注意的是“两个三角形两边及其一边对角对应相等,即为全等三角形”是假命题,也就是不能将“ASS”当作任意两个三角形是否全等进行判定的条件。
本文依托“几何画板”将图形的“运动”变化演示并展示给学生观看,简单化原本复杂的问题、具体化原本抽象的问题,同时在手写板的应用下将主干知识形成过程清晰地呈现给学生观看,突破重点、化解难点,激发学生兴趣及求知欲。
参考文献:
[1]王剑.关于全等三角形中“两边一角”问题[J].数学学习与研究,2016(15):122.
[2]邓昌滨.“边边角”能证明三角形全等吗?[J].中学数学教学参考,2015(Z2):45-46.
[3]熊莹盈.全等三角形判定定理的应用——“探究‘边边角在部分条件下证明三角形全等”教学设计[J].中国数学教育,2018(9):3-8.
[4]刘达.管窥数学探究活动课的典型特征——点评“探究‘边边角在部分条件下证明三角形全等”[J].中国数学教育,2018(9):9.
[5]李瑶,张红.数学任务框架案例分析与教学启示——以一堂“‘边边角能否判定三角形全等”公开课为例[J].中学数学研究(华南师范大学版),2017(2):5-7.
作者简介:
李建钢,浙江省杭州市,杭州市余杭区崇贤中学。

