2014版EAL算法中原子钟的权重分析

屈俐俐,李变

(1.中国科学院 国家授时中心,西安 710600；2.中国科学院 时间频率基准重点实验室,西安 710600)

0 引言

国际权度局(BIPM)基于全球70多个守时实验室自由运转的原子钟数据资料,采用ALGOS算法计算得到自由原子时(EAL),然后利用基准频标(PFS)对EAL进行频率修正后导出国际原子时(TAI)。

BIPM从1973年起采用ALGOS算法用于EAL的计算,计算时主要考虑EAL的长期稳定度。四十多年来,为了适用原子钟和比对链路性能的提升,BIPM对EAL的计算方法做过多次修改,其中针对ALGOS算法中的加权方法改进的次数最多。最近20年来BIPM对用于EAL计算的ALGOS算法(以下简称“EAL算法”)做过几次大的修改,第一次是在1996年将计算周期由每两月改为每月计算一次[1],数据点的间隔由每10 d改为每5 d；第二次是在1998年,对算法中的权系统做了调整,由最大绝对权重改为最大相对权重[2]；第三次是2001年最大权采用ωmax=A/N,其中N是每月参加EAL计算的钟的数量,A是经验值[3]；最近一次BIPM对EAL算法进行修改是2014年[4],本文主要针对2001年和2014年权重算法修改前后,参与EAL计算的原子钟权重结构进行分析研究。

1 EAL算法

EAL算法自1973年以来,期间经过几次修改,但每次修改只是少许调整(计算间隔改变、相对权重替代绝对权重和最大权原则等),一直沿用至2013年。该算法对于没有频率漂移,并且主要表现为随机游走频率调制噪声的原子钟(如：铯原子钟)是非常适合的。然而,目前参与EAL计算的原子钟除了5071A铯原子钟以外,还有大量的氢原子钟。这种以微波激射振荡器为基础的自激型频标,因具有极纯的信号频谱表现出非常优秀的短期稳定度。但是因物理结构及自身工作特性,氢原子钟存在频率漂移,且频率漂移量相对稳定。为了充分发挥氢原子钟的优势,G.Panfilo等人针对2001版EAL算法中的取权方法与频率预报方法提出了相应的改善方法。

1.1 2001版的EAL算法

为了提高时间尺度的可靠性,2001版EAL算法是在原算法的基础上,增加了最大权限制原则,解决了时间尺度过多依赖某一台性能优秀的原子钟的问题。之后该算法也被大多数时间实验室用于地方原子时的建立。

1.1.1 2001版的时间尺度计算方法

2001版的时间尺度计算方法基本公式如下[5]：

(1)

xi(t)=EAL(t)-hi(t),

(2)

hi′(t)=ai(t0)+Bip(t-t0),

(3)

式(1)～(3)中:hi(t)为钟i读数；xi(t)是EAL(t)和hi(t)的差；hi′(t)是hi(t)预测值；ai(t0)是钟i相对于EAL(t)在时刻t0的相位差；Bip(t)是钟i相对于EAL(t)在[t0,t]的预报频率；ωi(t)表示钟i的权重。

EAL每个月计算一次,采用的数据是通过远程时间比对得到的各守时实验室的钟与UTC(PTB)的比对结果,数据间隔5 d,数据点对应的时刻是约化儒略日(MJD)尾数为4和9的UTC 00:00的标准历元。

计算所用的方程为：

Xij(t)=xj(t)-xi(t),i=1,2,…,N,i≠j,

(4)

(5)

t=t0+mT/6,m=0,1,…,6,T=30 d,

(6)[注]在实际计算中,一年中某个月会出现T=35 d的情况,这时t=t0+mT/7,m=0,1,…,7。

式(4)～(6)中,t0是上个时间段的最后一个归算历元,也是本次计算的第一个归算历元,t是计算EAL的时刻,T是当前计算的时间段。N是参加计算的原子钟数,ωi(t)表示钟i的权重。当前时间段[t0,t0+T]的预报速率Bip(t)等于前一时间段[t0-T,t0]上的速率。

1.1.2 2001版的权系统计算方法

(7)

式(7)中,k为时间段索引,Bip,Ik(t)是钟i在时间段Ik内的速率值,< >表示统计平均。

权值计算公式为:

(8)

虽然性能优秀的钟应该对EAL的贡献更大,但是会导致EAL对性能优秀的极少数原子钟的依赖性过大,降低EAL的可靠性,所以对单钟的最大权进行限制。ωmax表示最大权,当ωi(t)≥ωmax,则ωi(t)=ωmax。

ωmax=A/N,

(9)

式(9)中,A为经验常数,在2014版算法之前,A值采用2.5,N是参加计算的钟数。

1.2 2014版的EAL算法

2001版的EAL算法,速率预报只考虑钟的相位和频率影响,即一次预报模型,不考虑频率漂移。而2014版的EAL算法中速率预报算法加入二次项来描述钟的频率漂移,也就是钟性能采用二次预报模型。

1.2.1 2014版时间尺度计算方法

2014版的hi(t)预测公式如下[6-7]：

(10)

(11)

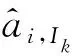
ai,Ik(tk)=EAL(tk)-hi(tk)=xi(tk)。

(12)

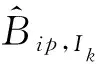
(13)

新增加的频率漂移参数的求解如下：

(14)

1.2.2 2014版权系统计算方法

在原子时尺度算法中,每个钟的权重与钟的频率稳定度成反比。2014版的权重算法更注重钟频率的“可预测性”,因此,只要钟的频率漂移足够稳定,那么它的频率预测值和实际测量值的偏差就很小。氢原子钟通常存在明显的频率漂移,且频率漂移的不确定性很小,所以在新算法中氢钟会获得较大的权重。

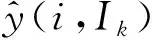
(15)

式(15)中,下标i表示第i台钟,Ik表示计算时间间隔。

2014版算法认为新的测量数据具有更可靠的统计特性,因此距离计算时刻越近的测量数据应该给予较大的权重,计算公式如下：

(16)

式(16)中,下标i是第i台钟,j代表计算间隔,Mi代表月份,BIPM时间部规定原子时的计算至少需要累积4个月的数据资料,因此4≤Mi≤12。

为了避免某个钟权重过大,2001版与2014版均采用最大权限制原则。根据文献[6-7],公式(9)中A值由原来的2.5改为4。

2 权系统修正前后原子钟的取权结构分析

Panfilo.G.等人在2014版EAL算法中,针对氢原子钟具有良好短期稳定度及频率漂移相当稳定的特点,对2001版EAL算法中权重计算提出了相应的改善方法,以提高氢原子钟在EAL计算中的权重。

2.1 EAL计算中的权分布

为了避免更换算法对EAL稳定度的影响,BIPM采用2006年至2013年的历史数据进行试算,文献[4-6]的结果表明：2014版采用平衡了氢钟和铯钟的权重分布的算法,提高了氢钟在EAL计算中的权重。图1和图2是BIPM分别采用2001版和2014版EAL算法,计算EAL时不同类型原子钟的权重分布情况。

图1 2001版EAL算法中权重的构成 图2 2014版EAL算法中权重的构成

图1中基准频标(PFS)的权重为3.8%,铯钟(Cs)的权重高达86.4%,而氢钟(HM)的权重只有9.8%。图2是2017年4月BIPM采用2014版算法计算EAL时不同类型钟的权重分布情况,其中基准频标占4.6%,铯钟的权重降低到25%,而氢钟的权重提高到70.4%。不同版本算法中基准频标所占权重份额较低、量值相对稳定,且与本文分析内容关系较小,所以后面的分析忽略与基准频标相关的内容。

2.2 原子钟类型与权重关系

由于每月参加EAL计算的原子钟数量不完全相同,总钟数呈缓慢增加趋势,且不同类型原子钟数量的比例关系也不完全确定,因此分析历年来不同类型原子钟的权重结构变化,只能基于不同类型原子钟数量的变化比例和权重变化比例的增量来衡量。

图3和图4分别是氢钟和铯钟在2009年至2017年参加EAL计算时,氢钟和铯钟的数量及它们所取权重的比例关系图。

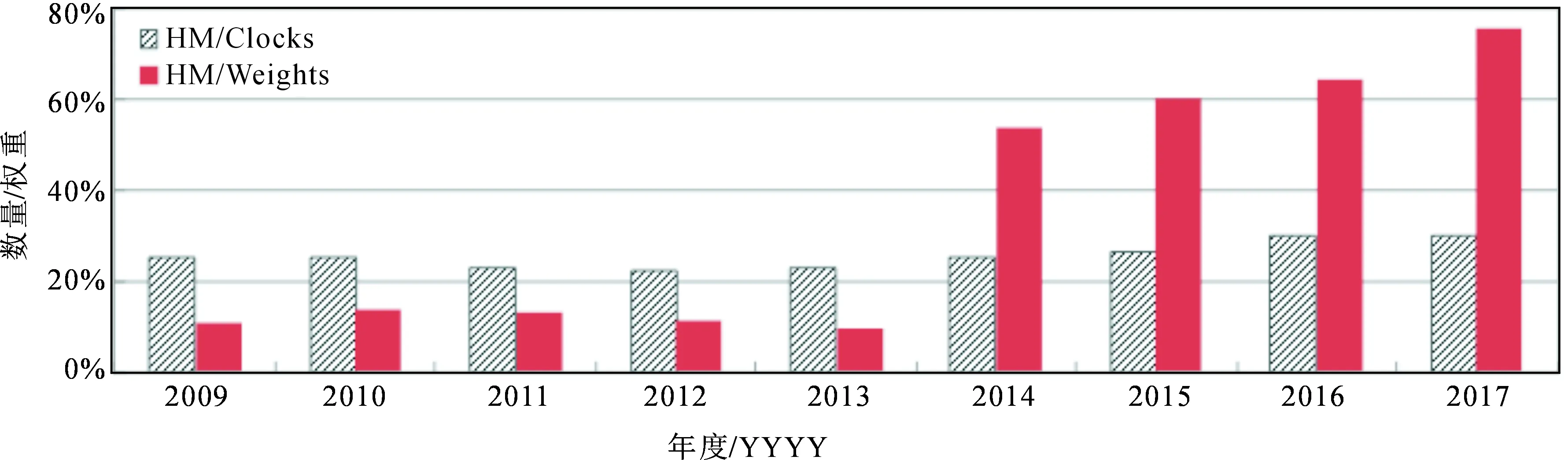
图3 2009-2017年参加EAL计算的氢钟数量及其权重比例

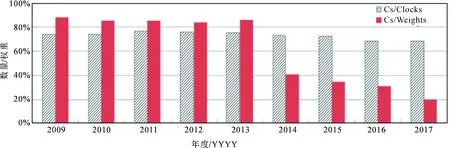
图4 2009-2017年参加EAL计算的铯钟数量及其权重比例

由图3和图4可以看出：①2009年以来氢钟占总钟数数量比例增加不到10%,但氢钟所占权重比例在采用2014版算法后,从2014年前的10%～15%,大幅度提高到54%,并且之后一路走高,在2017年氢钟所占权重超过了75%；②2014年之前,铯钟数量占总钟数的75%左右,权重基本保持在总权重的85%～88%之间,采用2014版算法后,铯钟的权重大幅下降,目前约占总权重的20%。

为了分析2014版算法使用前后氢钟和铯钟对EAL的贡献,本文定义钟的效率=权重/数量(只针对取到权的钟),统计结果如下：2009年至2013年,氢钟的效率是50%,铯钟的效率是114%；2014年至2017年,氢钟的效率是227%,铯钟的效率是45%。即氢钟的效率提高了3.54倍,铯钟的效率降低了1.53倍。

2.3 不同取权区间内钟的权重分布

在EAL计算中,利用公式(10)计算出的最大权每月并不相同,为了统计方便在本文中对权重进行归一化计算,最大权为1。为了下面分析的需要,将权重区间按0.2间隔划分,即ω=0(取0权的钟),0<ω≤0.2,0.2<ω≤0.4,0.4<ω≤0.6,0.6<ω≤0.8,0.8<ω<1,ω=1(取最大权的钟)。

图5和图6分别是2011年至2017年EAL计算中,不同权重区间内的原子钟数量占总钟数的百分比和原子钟权重占总权重的百分比。

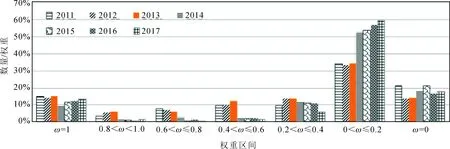
图5 2011-2017年不同取权区间内原子钟数量的分布

由图5可以看出：①两种算法在ω=1,0.2<ω≤0.4和ω=0 3个权值区间内,原子钟数量所占比例相当；②2014版算法在0.8<ω<1,0.6<ω≤0.8和0.4<ω≤0.6 3个权值区间内,原子钟数量所占比例明显低于2001版算法：2014版算法中落在这3个权值区间内钟数量总和所占比例不足5%,而2001版算法中钟数量总和所占比例约为25%；③在0<ω≤0.2权值区间,2014版算法中钟数量所占比例超过50%,2001版算法中钟数量所占比例约为35%。

图6 2011-2017年不同权值区间内钟权重的分布

如图6所示：①2001版算法中取得最大权(ω=1)的钟所占的权重比例约为40%,且该比例比较稳定；②在采用2014版算法后,取得最大权(ω=1)的钟所占权重的比例从2014年的55%左右开始逐年增长,到2017年达到64%左右；③在0<ω<1区间,2001版算法中权值分布比2014版算法更合理。

2.4 不同取权区间内钟类型的分布

图7和图8分别是2011年至2017年在EAL计算中,氢钟和铯钟在不同权值区间钟数量的分布比例。

由图7可知：①在ω=1权值,2001版算法中氢钟数量约为10%,2014版算法中氢钟数量在40%左右；②在0<ω≤0.2权值区间,2001版算法中氢钟数量超过50%,2014版算法中氢钟数量在25%左右；③在其他权值区间,两种算法中氢钟数量相当。

由图8可知：①在ω=1权值,2001版算法中铯钟数量约为15%,2014版算法中铯钟数量小于1%；②在0<ω≤0.2权值区间,2001版算法中铯钟数量小于35%,2014版算法中铯钟数量在70%左右；③在0.4<ω≤0.6,0.6<ω≤0.8和0.8<ω<1权值区间,2001版算法中铯钟数量总和在30%左右,2014版算法中铯钟数量总和小于4%；④在0.2<ω≤0.4权值区间,两种算法中铯钟数量相当。

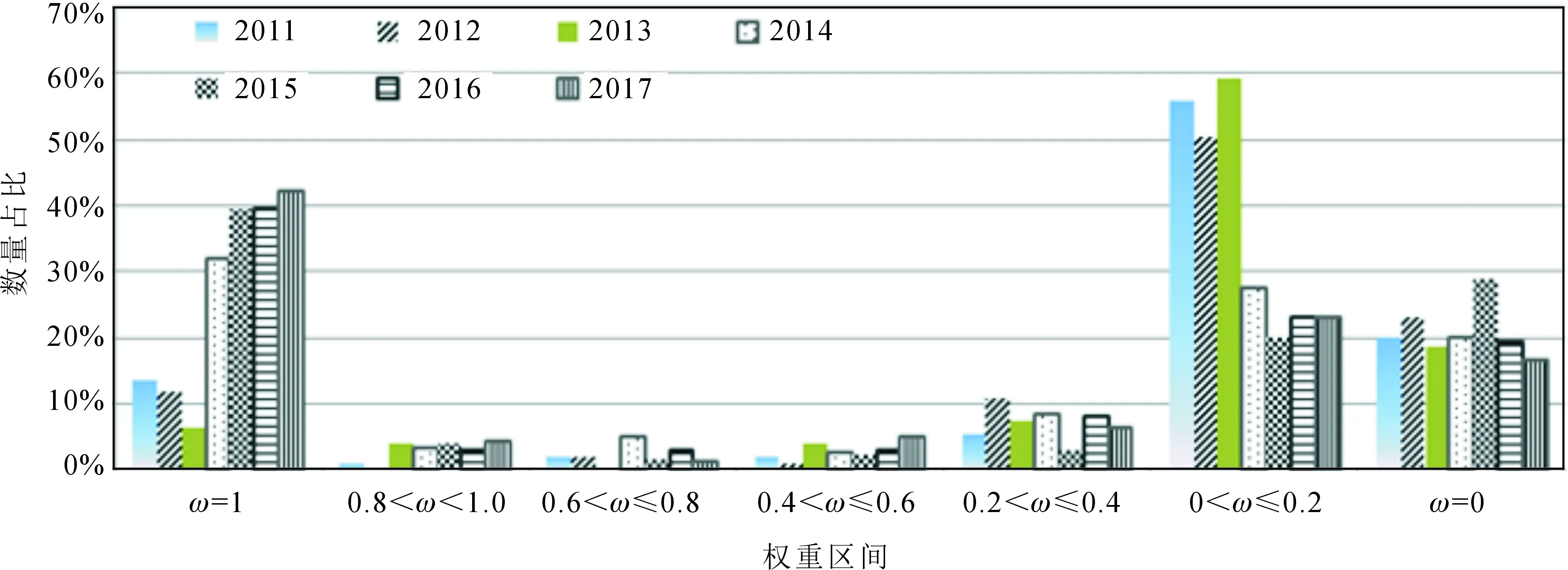
图7 2011-2017年EAL计算中氢钟在不同权值区间占氢钟总数比例

图8 2011-2017年EAL计算中铯钟在不同权值区间占铯钟总数比例

3 结论

参与EAL计算的原子钟数据来源于全球70多个守时实验室,这些实验室配置的守时原子钟主要是铯原子钟和主动型氢原子钟,这两类钟占参与EAL计算的总钟数的98%,一般情况下,氢钟的数量占总钟数的1/3。

铯钟频率波动较大,几乎没有频率漂移；氢钟存在频率漂移,但大多数氢钟的频率漂移量相对稳定。因此氢钟在采用2014版算法计算EAL时,可以取得较高的权重。

BIPM提出2014版算法的目的是：①利用氢钟良好的频率预测特性,提高EAL的稳定性和准确度,这已在BIPM相关文献中证明[6,8-11]；②平衡氢铯两种原子钟在EAL计算时的权重比例。

通过分析2014年以来3年多EAL的计算结果,该算法首先提高了氢钟在计算EAL时的权重,氢钟权重份额在这3年当中呈现不断增长的趋势,从2014年的54%提高到2017年的75%,权重在3年间增加了21%,况且根据图3和图4该比例仍将会继续提高,这样,未来几年很有可能会出现EAL算法修改前的铯钟权重完全占据主导地位的状况,只不过这次是由铯钟更换为氢钟而已；其次,2014版算法中取最大权(ω=1)的钟数量不超过15%,但是所占权重比例过高；权值在0<ω≤0.2区间的钟数量偏大；在0.2<ω<1区间的钟数量甚少。这是由于最大权门限和经验常数A不匹配导致的,关于二者关系的分析将在另一篇文献中给出。

通过以上的分析,对采用类ALGOS算法中权重的确定提出以下建议：

①依据守时钟组的配置情况,适当平衡不同类型钟的权重；

②确定取最大权钟的数量及其所占权重份额,取最大权的钟的数量不超过总钟数的15%,所占权重份额约50%左右为宜[11]；

③分析落在不同权值区间钟的数量、钟类型的分布状况,避免出现2014版算法中两头过大,中间区域几乎没有钟的超级哑铃状的情况出现；

④算法投入使用前,应对算法使用后可能出现的状况进行评估,避免权重份额出现趋势性改变;

⑤经验常数A的确定需经过大量试算。A值过大会使计算的时间尺度只依赖于少数性能好的钟,从而降低时间尺度的可靠性；反之,又会使性能优秀的钟对时间尺度的贡献过小,降低时间尺度的准确性和稳定性。

综上所述,守时实验室在借鉴其他时间尺度算法时,不可直接照搬,需结合自身原子钟资源的情况进行详细分析并进行大量试算,最终找到满足守时实验室要求的时间尺度算法。