基于VGOS的GEO卫星观测试验

弓剑军,马浪明,姚当,杨旭海

(1.中国科学院 国家授时中心,西安 710600；2.中国科学院 精密导航定位与定时技术重点实验室,西安 710600；3.中国科学院大学,北京 100049)

0 引言

地球同步卫星(geostationary earth orbit,GEO)独特的高轨和静地特性,使其在卫星导航领域发挥着重要作用,是我国导航系统空间段的重要组成部分。近年来,VLBI(very long baseline interferometry)在卫星轨道测量方面,例如月球探测和深空探测,均发挥重要作用。正如距离测量和多普勒测量决定飞行器视向约束,VLBI决定飞行器横向约束。VLBI测量是距离测量和多普勒测量的补充[1],VLBI观测能直接提供目标源角位置的几何约束。

精确的VLBI时延模型对于VLBI数据处理、分析都至关重要。VLBI观测同步卫星时,必须要考虑近场时延模型的影响。Fukushima,Sovers分别提出了有限距离射电源的VLBI延迟模型[2-3]。Moyer基于光行时方程开发了近域延迟模型[4]。Sekido提出了基于分析法的有限距离射电源时延模型[5]。

R.A.Preston等利用VLBI技术对地球同步轨道卫星进行观测,时延测量精度为0.15 ns[6]。T.SHIOM采用D-VLBI方法对同步卫星进行观测,观测精度约为2 ns,并采用D-VLBI与无线电测距对同步卫星进行联合定轨,卫星轨道精度为100 m[7]。舒逢春利用中国VLBI网对同步卫星进行差分观测,并成功获得条纹[8]。吕林蔚等利用3.7 m天线开展VLBI观测同步轨道卫星试验[9]。黄勇等利用中国VLBI网(口径25 m)和转发式测定轨系统联合对GEO导航卫星进行观测试验,并利用VLBI测轨数据和C波段转发式测距数据进行联合定轨分析,综合两种类型数据联合定轨可以显著提高同步卫星机动后轨道的快速恢复及定轨预报精度[10]。Lucia Plank利用VLBI天线观测GNSS卫星,并成功获得观测条纹[11]。

1 VLBI观测原理

VLBI用相距甚远的两面天线,接收某射电源或飞行器的信号,如图1所示。射电源或飞行器的信号经过长距离的传输,其波前到达两天线的时间差即为此处的时延τ：

τ=-B·cos(θ)/c,

(1)

式(1)中,B为基线长度,θ为天线与基线的夹角,c为光速。

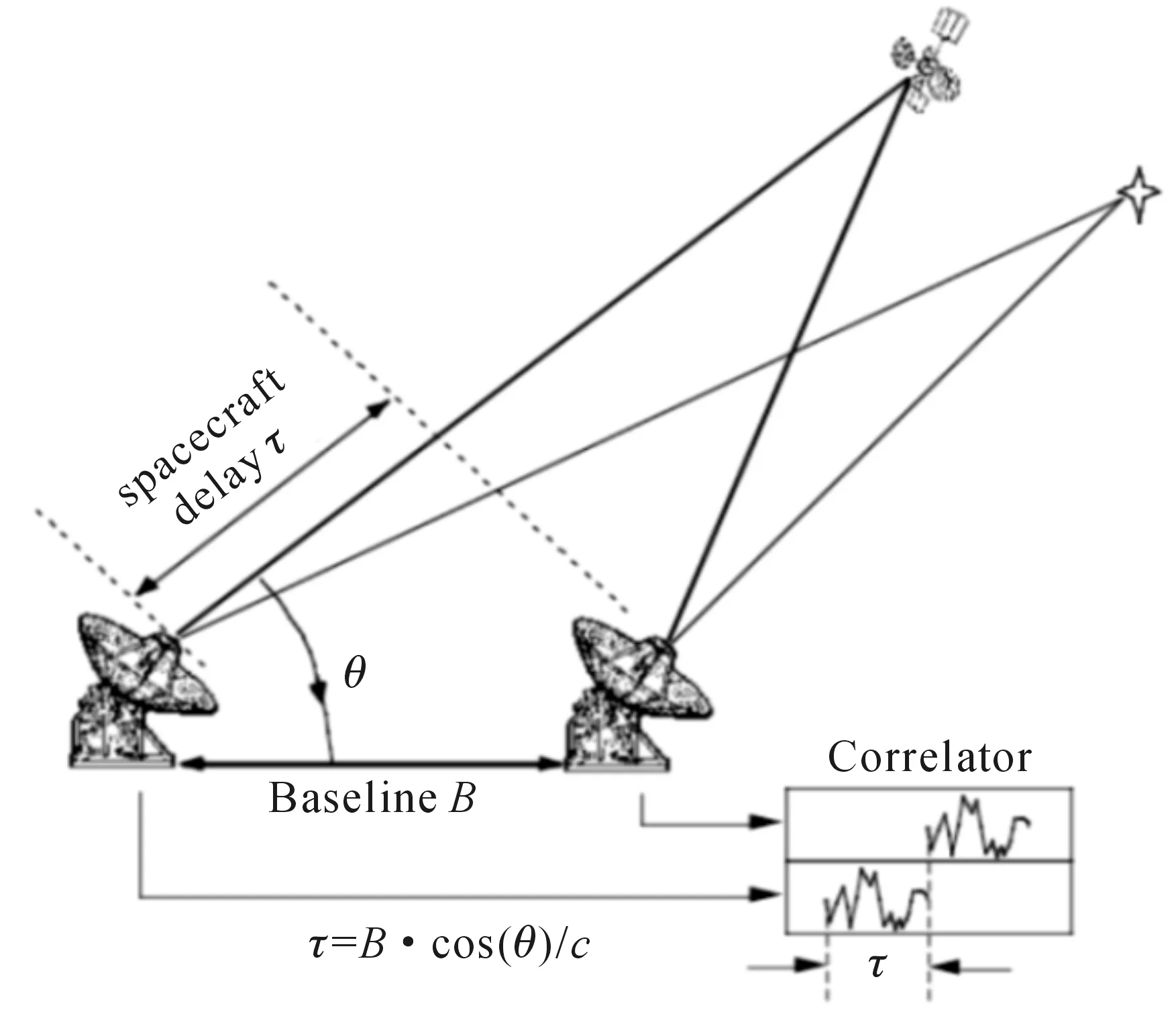
图1 VLBI测量原理图

射电源信号到达2个天线时的波前可认为是平面波,而同步卫星信号到达2个天线时,波前则是球面波。在对卫星信号处理时,必须要考虑球面波带来的影响。

天线温度指天线指向射电源或飞行器时,射电源或飞行器辐射所贡献的天线温度。天线温度Ta可以定义为

(2)

式(2)中,Ae为天线有效面积,表示天线截取信号的实际面积。S为观测源的流量密度,单位为央斯基,k为玻尔兹曼常数。

VLBI互相关函数的相关系数ρ0(归一化相关幅度通常用相关系数来表示)的计算公式如下：

(3)

式(3)中,Ta1,Ta2分别是天线1,2的天线温度,Tn1,Tn2分别是天线1,2的天线噪声温度。

VLBI测站接收到的射电波信号是由信号和噪声两部分组成的,信噪比可以表示为

(4)

式(4)中,ρ0为相关系数,q为数据量化和相关处理的相关系数下降因子,B是观测带宽,T是积分时间。

当Tn1,Tn2≪Ta1,Ta2,可以得到

(5)

单通道的群时延定义为条纹相位随频率的变化率,表示为

(6)

式(6)中,φ为条纹相位,ω为频率。

单通道时延测量精度为

(7)

式(7)中,B为观测带宽,SSNR为信噪比。

时延率定义为条纹相位相对于时间的变化率,则时延率为

(8)

式(8)中,φ为条纹相位,ω为频率,t为时间。

在观测飞行器时,通常需要观测目标源的流量密度。飞行器的信标为点源,等效流量密度S为

(9)

式(9)中,PEIRP为下行信号的有效发射功率；Ls为各种损耗(如：大气衰减、馈线损耗、极化损耗等)总和；B为信号带宽；d为地面VLBI观测站到目标源距离。

1.1 近场时延算法

VLBI观测同步卫星时,需要考虑波面的弯曲效应,如图2所示。假设电磁波信号在时间t0从观测源O发射,到达天线1和天线2的时间分别为t1和t2。这样信号到达2个天线的时延可以表示为

(10)

式(10)中

(11)

(12)

式(12)中,Δt0,atm表示中性大气引起的时间误差,Δt0,ion表示电离层引起的时间误差,Δt0,inst表示设备引起的时间误差,Δt0,GR表示相对论效应引起的时间误差。公式(10)～(12)是VLBI观测有限距离源的观测方程。

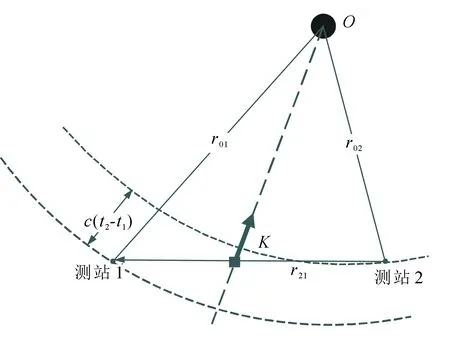
图2 近场时延示意图

相对论效应改正可以表达为：

(13)

(14)

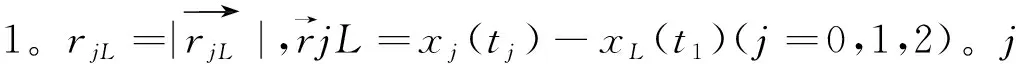
2 观测试验

利用中国科学院国家授时中心新建的3套VGOS系统[13-14]对中星12号卫星进行观测,并对观测精度进行分析。

2.1 VLBI观测网

中国科学院国家授时中心VGOS系统包括：吉林、三亚和喀什3个测站和西安数据处理中心,3个测站与西安数据处理中心之间通过专用网络传输观测数据。3个测站均装备13 m口径天线、双圆极化的频带覆盖范围1.2～9 GHz宽频带致冷接收机、数据采集终端、高稳定氢原子钟等设备,西安数据处理中心建有3台站硬件相关处理系统、纲要软件服务器、测站监控软件、DiFX[15-17]相关处理软件系统和HOPS(haystack observatory postprocessing system)相关后处理软件[18]。

2.2 宽带VLBI观测同步卫星试验

2016年10月16日,利用中国科学院国家授时中心VGOS对中星12号卫星的C波段转发器的下行信号进行观测,观测带宽为16 MHz,信号中心频率为3 822 MHz,数据采样率为2 bit,观测时间为5 s。

中星12号卫星转发器波束中心EIRP为41 dBW,中国周边为39 dBW。通过公式(9)计算,中星12号卫星的等效流量密度示于表1。

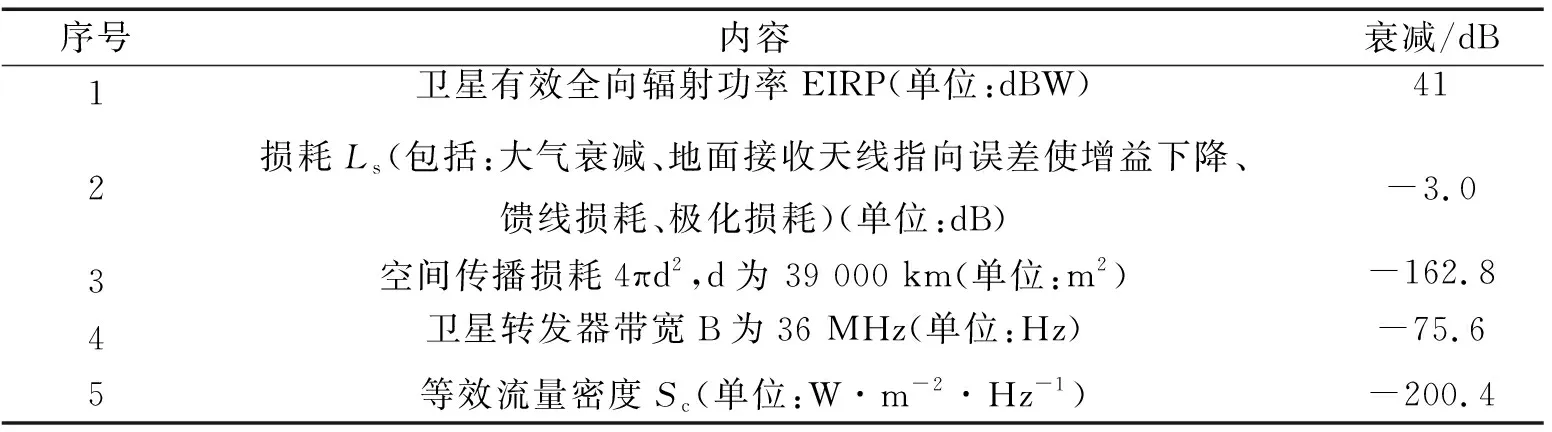
表1 中星12号卫星等效流量密度

将中星12号卫星的等效流量密度的单位转化为央斯基：912 010.8 Jy。宽带VLBI天线口径为13 m,根据公式(2),可以计算出中星12号卫星辐射所贡献的天线温度Ta为87 512 K,宽带VLBI天线的噪声温度为Tn为50 K,由此可见Tn≪Ta。计算信噪比采用公式(5),数据采样率为2 bit,数据量化和相关处理的信噪比下降因子q为0.88,观测带宽为16 MHz,积分时间为5 s,由此可以计算出信噪比为11 131。将此信噪比带入式(7)可得,卫星时延测量精度στ=3.1 ps。

3 试验数据处理及分析

由于DiFX软件主要针对射电源数据进行相关处理,使用的时延模型适合处理射电源观测数据。在DiFX处理中星12号卫星的观测数据时,用中星12号卫星的近场模型文件替换DiFX原有的射电源时延模型文件,从而能够对卫星观测数据进行相关处理。

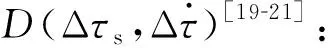
(15)

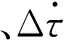
选取2016年10月16日17:00～17：05时间段的VLBI观测卫星的数据进行分析。图3为喀什、三亚和吉林观测中星12号的自相关谱,横轴表示带宽,单位为MHz,纵轴表示代表自相关幅度。

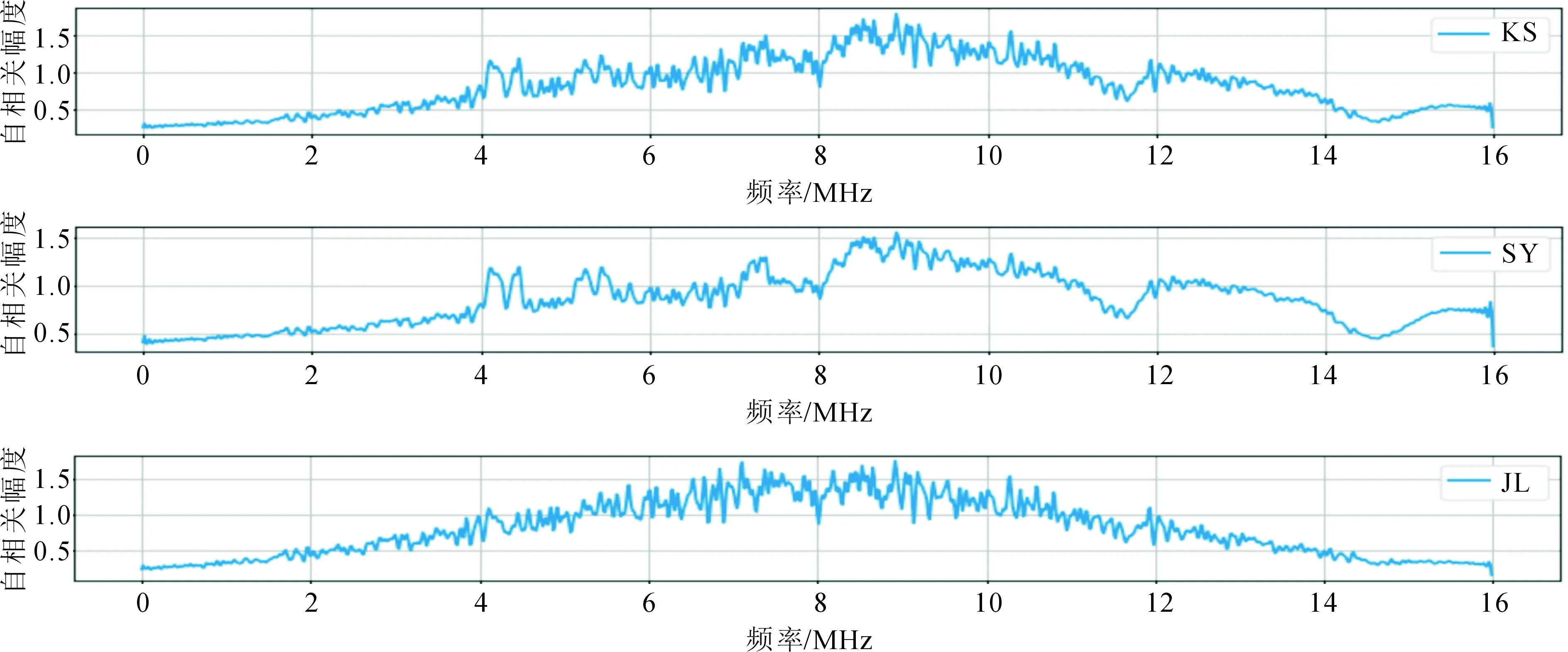
图3 喀什、三亚和吉林观测中星12号卫星的自相关谱

从图3中可以看出喀什站和三亚站观测中星12号卫星的自相关谱的形状基本相同。主要原因是喀什站的VLBI天线与转发式测轨站并址,三亚站也是如此。VLBI天线受到转发式测轨站的电磁干扰,使得自相关谱的幅度发生变化。而吉林站电磁环境比较好,整个自相关幅度比较平稳。

图4～6表示在条纹拟合过程中,在时延-时延率平面上搜索到的互相关函数幅度的最大值。上图表示互相关函数的幅度最大时,相对应的时延值,横轴表示时延,单位为μs,纵轴表示互相关函数的幅度。下图表示互相关函数幅度最大时,对应的时延率值,横轴表示时延率,单位为ns/s,纵轴表示互相关函数幅度。

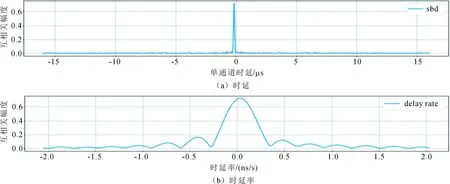
图4 吉林-喀什基线时延、时延率图

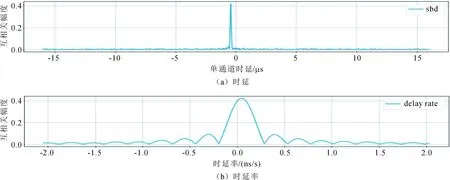
图5 吉林-三亚基线时延、时延率图

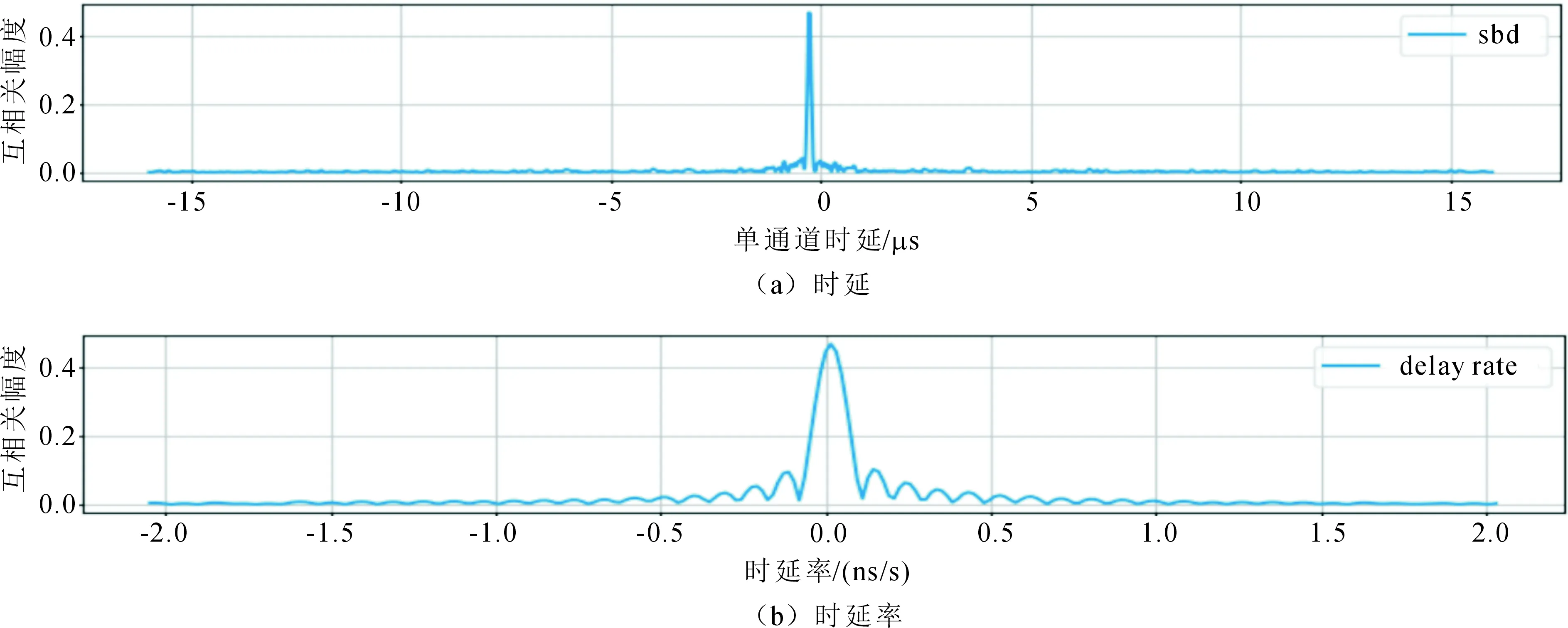
图6 喀什-三亚基线时延、时延率图

从图4～6中可以看出,吉林-喀什、吉林-三亚和喀什-三亚基线均成功找到互相关函数幅度的最大值,表示3条基线均成功观测到卫星条纹。由于互相关函数幅度的最大值即为互相关函数的相关系数,吉林-喀什、吉林-三亚和喀什-三亚基线的相关系数分别为0.722,0.474和0.42。

由于在观测中记录设备有丢包现象,2个观测站在进行互相关时,能够积分的时间均比观测时间短。从表2中可以看出,fourfit程序计算的吉林-喀什、吉林-三亚和喀什-三亚基线的时延精度分别为11,16和8.9 ps。从表3中可以看出,采用与表3相同的积分时间,通过公式(5)计算的吉林-喀什、吉林-三亚和喀什-三亚基线的时延精度分别为7.4,6.7和4.1 ps。由于在天线观测过程中,周围环境存在电磁干扰,而且在数据记录过程中丢包比较严重,吉林-三亚和喀什-三亚的基线计算的相关系数仅为理论的相关系数的50%左右,实测的时延测量精度为理论计算的精度40%左右,吉林-喀什基线计算的相关系数为理论的相关系数的82%,实测时延测量精度为理论计算的精度的67%。

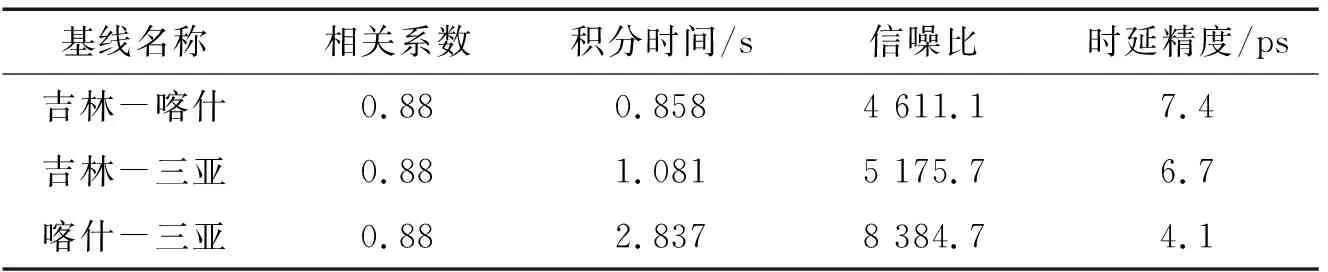
表3 理论计算的时延精度

4 结语

利用国家授时中心3台宽带VLBI天线对中星12号同步卫星进行观测,成功获得观测条纹,时延测量精度在10 ps量级。由于电磁环境的干扰和数据采集过程中存在丢包现象,使得实测的时延精度低于理论时延计算精度。后续将在抗干扰、数据传输等方面采取措施,提高国家授时中心VGOS系统的测量精度和可靠性。