中继式卫星双向时间比对研究

王威雄,董绍武,武文俊,广伟,姜萌,王翔

(1.中国科学院 国家授时中心,西安 710600；2.中国科学院 时间频率基准重点实验室,西安 710600；3.中国科学院大学 天文与空间科学学院,北京 101048)

0 引言

目前高精度时间在很多领域应用越来越广泛,这对远距离的时间比对技术也提出了更高的要求[1]。基于地球同步通信卫星的双向时间频率比对(two-way satellite time and frequency transfer,TWSTFT)是目前最准确的远距离时间比对技术之一,是参与国际原子时(TAI)计算的原子钟之间比对的重要手段,其时间比对准确度和频率稳定度分别优于1 ns和1×10-15(1 d)[2]。现德国技术物理研究所(PTB)是国际权度局(BIPM)指定的UTC唯一时间比对节点,因此世界主要时间实验室都与其建立双向链路进行比对[3],目前双向主要的比对链路如图1所示。

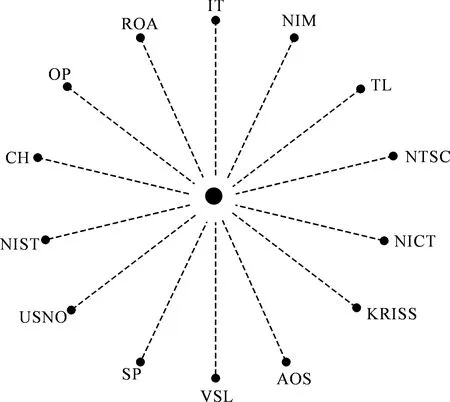
图1 世界上主要的卫星双向时间比对链路

TWSTFT会受到基线长度的限制,在相距较远的两个站之间不可能或难以用单个卫星建立直接双向比对链路,因此目前很多重要的时间实验室除与PTB有直接双向比对链路外,它们相互之间只能通过GNSS的方式进行时间比对[4]。为提高时间比对链路可靠性并满足特定需求,2006年美国海军天文台(USNO)、美国国家标准与技术研究院(NIST)、日本国家信息与通信技术研究所(NICT)与我国台湾地区中华电信股份有限公司(TL)就曾讨论在北美与亚洲之间建立间接双向链路的可能性[5]。更加重要的是,目前由于租用的俄罗斯AM-22卫星寿命到期,欧亚实验室正在测试新的卫星用于欧亚链路TWSTFT的重建,较长的基线可能导致亚洲时间实验室与PTB之间无法实现直接链路的双向时间比对,必须通过第三站中转来进行双向时间比对参与UTC计算[6]。因此,针对目前远距离时间比对的发展现状,文中采用了一种间接链路的方法来完成卫星双向时间比对,即以某个地面站为中继站,分别计算另外两个地面站与中继站的双向比对结果,抵消中继站的钟差后,间接获得两站之间的钟差。与常规TWSTFT相比,间接链路最大的特点是不再受基线长度的限制,并且不需要新的设备和另外的测试。实验以PTB为中继站,选取中国科学院国家授时中心(NTSC)与USNO,NTSC与瑞典国家技术研究中心(SP)分别为参与比对的两个地面站。最后,我们通过GPS精密单点定位(GPS PPP)时间比对结果对卫星双向间接链路进行了比对验证,并对间接链路的时间和频率不确定度进行分析。

1 TWSTFT基本原理

TWSTFT利用地球同步通信卫星(GEO)转发地面两个实验室的主钟时间信号,如图2所示。地面站1的主钟时间信号通过调制解调器经伪码扩频方式调制,通过甚小口径天线终端(VSAT)将调制的扩频信号发射给卫星,经卫星转发器把1站的时间信号转发至地面站2,地面站2接收经卫星转发的1站的时间信号,解调信号后与本地的原子钟信号相比较,获得1站至2站的信号传输时延。在1站发射信号的同时,2站以同样方式发射信号并且被1站接收。通过两站数据交换,获得两地原子钟间的高精度钟差[7]。

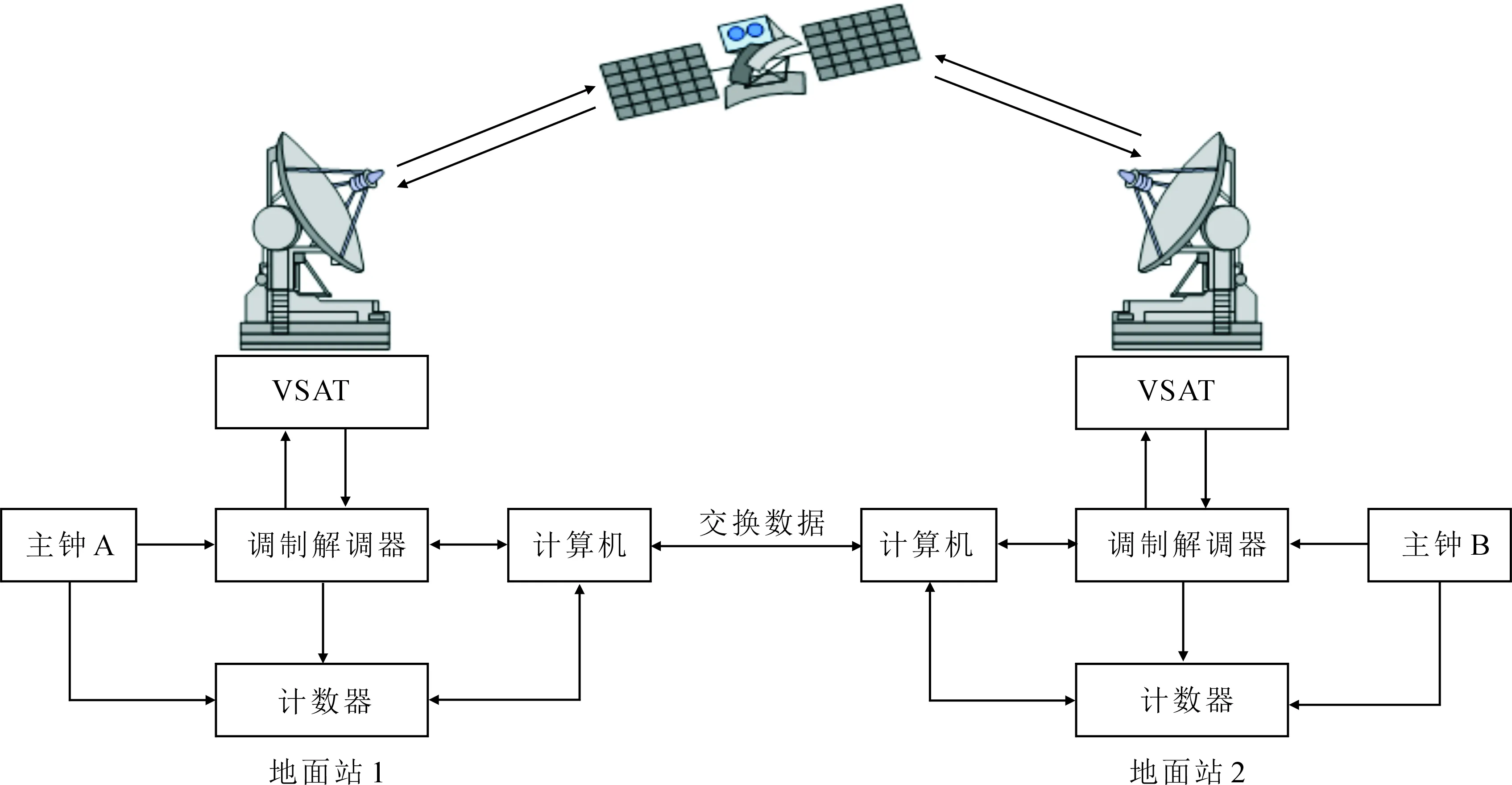
图2 卫星双向时间比对原理

卫星双向链路的各种信号延迟及信号流如图3所示[8],其中：

TTSk为本地时间尺度,k表示站1,2,下同；TTIk为地面站调制解调器测量值；TTXk为地面站发射通道延迟,包括调制解调器延迟；TRXk为地面站接收通道延迟,包括调制解调器延迟；TSGUk为信号几何路径上行时延；TSGDk为信号几何路径下行时延；TSTUk为对流层上行时延；TSTDk为对流层下行时延；TSIUk为电离层上行时延；TSIDk为电离层下行时延；TSPTk为通过转发器的卫星路径延迟；TSCUk为上行链路中的Sagnac校正；TSCDk为下行链路中的Sagnac校正。

由TTS1-TTS2表示的站1的时间尺度与站2的时间尺度之间的差值确定如下。

地面站1的调制解调器测量值：

TTI1=TTS1-TTS2+TTX2+TSGU2+TSTU2+TSIU2+TSCU2+TSPT2+TSGD1+TSTD1+TSID1+TSCD1+TRX1。

(1)

地面站2的调制解调器测量值：

TTI2=TTS2-TTS1+TTX1+TSGU1+TSTU1+TSIU1+TSCU1+TSPT1+TSGD2+TSTD2+TSID2+TSCD2+TRX2。

(2)

式(1)和式(2)相减,并整理得到：

TTS1-TTS2= 0.5TTI1-0.5TTI2+0.5(TSPT1-TSPT2)-0.5(TSCD1-TSCU1)+

0.5(TSCD2-TSCU2)+0.5(TSGU1-TSGD1)-0.5(TSGU2-TSGD2)+

0.5(TSTU1-TSTD1)-0.5(TSTU2-TSTD2)-0.5(TSIU1-TSID1)+

0.5(TSIU2-TSID2)+0.5(TTX1-TRX1)-0.5(TTX2-TRX2)。

(3)

式(3)中,0.5TTI1为地面站1的调制解调器测量值,0.5TTI2为地面站2的调制解调器测量值,0.5(TSPT1-TSPT2)为卫星转发器延迟,0.5(TSCD1-TSCU1)为站1 Sagnac校正,0.5(TSCD2-TSCU2)为站2 Sagnac校正,0.5(TSGU1-TSGD1)为站1几何路径时延,0.5(TSGU2-TSGD2)为站2几何路径时延,0.5(TSTU1-TSTD1)为站1对流层时延,0.5(TSTU2-TSTD2)为站2对流层时延,0.5(TSIU1-TSID1)为站1电离层时延,0.5(TSIU2-TSID2)为站2电离层时延,0.5(TTX1-TRX1)为站1设备时延,0.5(TTX2-TRX2)为站2设备时延。

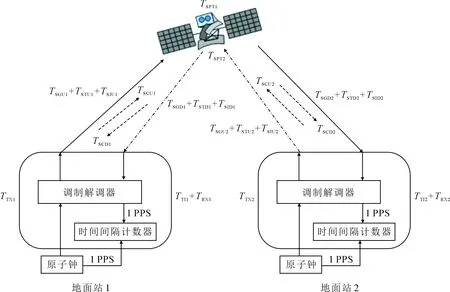
图3 卫星双向时间比对信号流

PTB与USNO,SP和NTSC之间分别都有直接双向比对链路,通过PTB中转,可以得到USNO与NTSC,SP与NTSC之间的间接链路比对结果,原理图如图4所示。公式如式(4)和式(5)所示：

UTC(USNO)-UTC(NTSC)=(UTC(USNO)-UTC(PTB))+(UTC(PTB)-UTC(NTSC)),

(4)

UTC(SP)-UTC(NTSC)=(UTC(SP)-UTC(PTB))+(UTC(PTB)-UTC(NTSC))。

(5)

由于NTSC-PTB链路与USNO-PTB,SP-PTB链路租用不同的GEO通信卫星且属于不同的洲际链路,测量数据的时标与NTSC-PTB的时标不同,所以必须采用插值的方法得到与NTSC-PTB比对链路时标一致的USNO-PTB和SP-PTB链路双向比对值,然后获得间接卫星双向时间比对的结果。

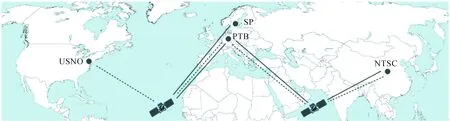
图4 PTB为中继站的卫星双向时间比对链路图

2 误差分析及数据处理

为了得到精确的间接卫星双向时间比对结果,对比对链路中影响时间比对精度的主要误差源进行分析,并阐述观测数据的处理流程。

2.1 误差分析

卫星双向时间比对的精度与传输路径上的误差测量精度密切相关。在卫星双向时间比对中,由于信号传播路径的近似对称性,信号在传输路径上的误差大部分被抵消,这是卫星双向时间比对的技术优势,本节主要分析各种误差对卫星双向时间比对的影响。

2.1.1 对流层延迟

对流层延迟与观测卫星的仰角有关,也与空气中的水含量、空气密度和温度等参数有关,但是在信号频率小于20 GHz时,该延迟可以认为和信号频率没有关系[7]。

2.1.2 电离层延迟

在TWSTFT过程中,为了避免信号间的相互干扰,上行链路与下行链路的频率并不相同。电离层的延迟Δion与信号频率和信号路径上的总电子含量(TEC)相关[9],表达式如下：

(6)

式(6)中,TTEC为沿信号路径的总电子含量,c为光速,fd和fu分别是下行链路和上行链路频率。C波段TWSTFT链路在中纬度地区的影响小于0.5 ns,在低纬度地区由于太阳对电离层影响较大,可能大于0.5 ns。对于Ku波段(频率远高于C波段)的影响比C波段的影响小的多[7]。

2.1.3 设备延迟

设备时延误差是TWSTFT中的重要误差源,主要包括地面站计数器测量误差、卫星转发器时延误差和地面站发射通道与接收通道硬件时延误差[10]。其中最主要的误差是地面站发射通道与接收通道硬件时延误差。修正方法有绝对校准测量和相对校准测量两种[11]。目前世界上主要采用相对测量法进行校准,相对测量法包括TWSTFT移动校准站和GPS移动校准站。

2.1.4 Sagnac效应

由于地球自转和光速不变,信号在从地面站发射到卫星和从卫星发射到地面站的过程中,传播路径会发生变化,并非是某一时刻星地间的距离。信号从地面站传播到卫星的实际时延与某一时刻两者之间的信号传播时延的差称为Sagnac效应[12],处理方法是利用算法将Sagnac效应计算出来并加以修正。

2.1.5 卫星运动的影响

地球静止轨道卫星在只受均匀地球引力的情况下,它相对于地面静止不动。但事实上,由于各种卫星摄动力的存在,它相对于地面做日周期运动[13]。卫星运动会造成信号传播路径中的上下行几何路径不相等,从而带来误差,消除方法可以采用双向链路单条通信链路上历元间的伪距差分求解卫星对TWSTFT的影响。

2.1.6 卫星转发器的影响

卫星双向时间比对中使用的是透明转发器,它能够接收来自地面的信号并且将该信号变频放大转发向地面,在空中主要为信号起桥接作用。一般情况下,TWSTFT两站共用同一转发器,两站信号通过卫星转发器的时延可以直接相互抵消,不需要对其做特殊处理[14]。

2.1.7 各误差项的处理方式

各种误差源对于TWSTFT影响不同,目前国际上主要采用KU波段进行卫星双向时间比对。在KU波段下,式(3)中两站的几何路径时延、对流层时延和电离层时延可以忽略不计,卫星转发器时延可以相互抵消,Sagnac效应可以通过具体的模型修正,比对两站的设备时延需要准确校准,TWSTFT过程中,具体对误差源的处理方式如表1所示[15]。

表1 TWSTFT中主要误差源及其修正方式

2.2 数据处理

为了便于对比对数据进行处理,国际电信联盟(ITU)发布了建议书来统一定义TWSTFT数据格式。该文件包括卫星参数、本地站与远程站站名、信号频率、设备校准、时间比对测量值等信息。要计算两地的钟差,只需要将两个站的数据交换并按规定进行处理即可[8]。

3 结果分析

实验处理了NTSC-PTB和USNO-PTB链路从2017年1月3日到1月17日(MJD 57 756～57 770)连续15 d的数据以及NTSC-PTB和SP-PTB链路从2017年5月30日到6月18日(MJD 57 903～57 922)连续20 d的数据。利用3次样条插值的方法得到与NTSC-PTB双向比对结果时标相同的USNO-PTB和SP-PTB的双向链路结果。图5和图6分别为同一时间段内的NTSC-PTB链路的比对结果和USNO-PTB链路的原始比对结果与内插结果,图7和图8分别为同一时间段内的NTSC-PTB链路的比对结果和SP-PTB链路的原始比对结果与内插结果,圆圈为原始结果,星点为内插结果。

图5 NTSC-PTB链路的双向时间比对结果

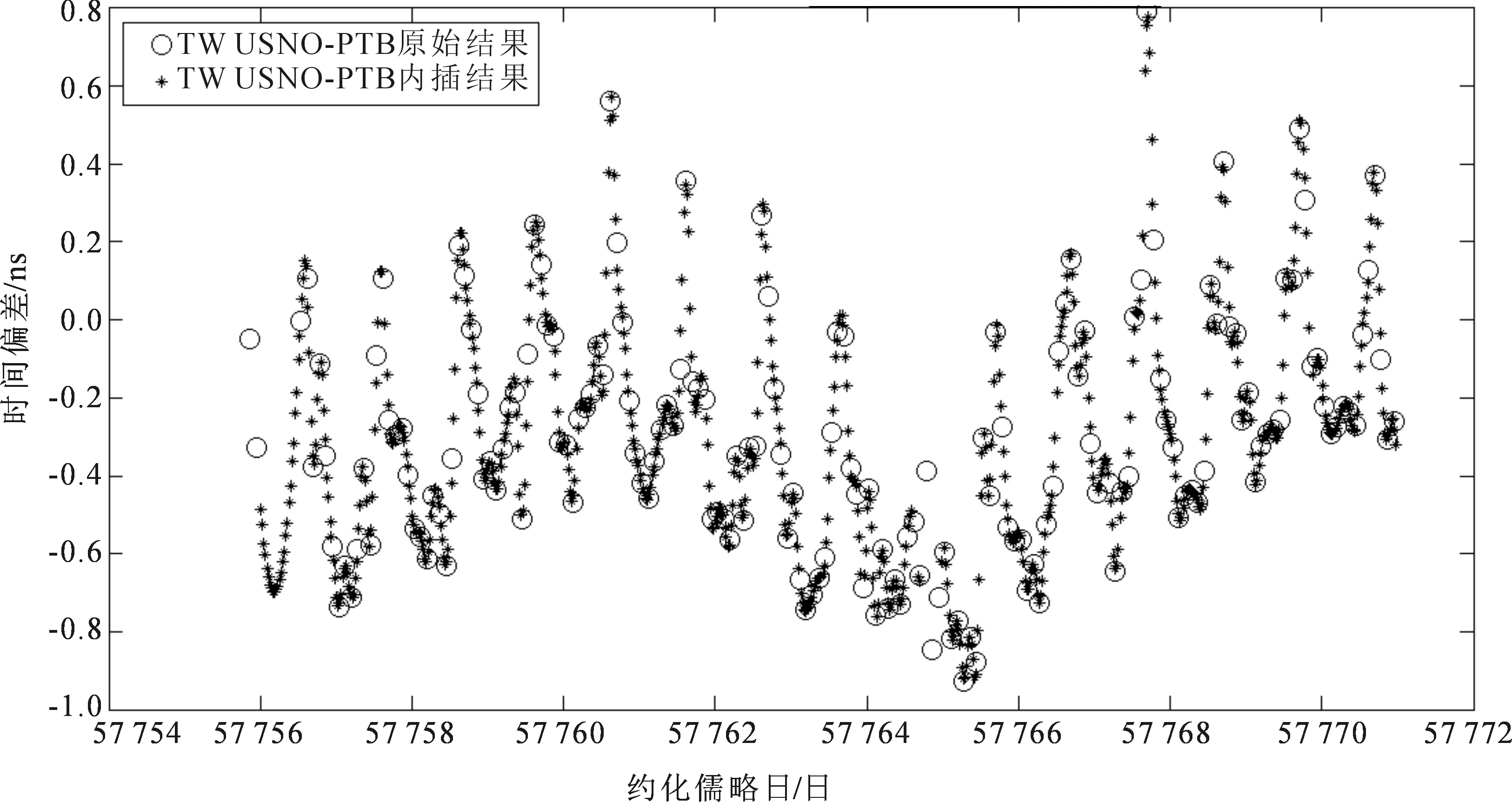
图6 USNO-PTB链路的原始结果和内插结果

图7 NTSC-PTB链路的双向时间比对结果

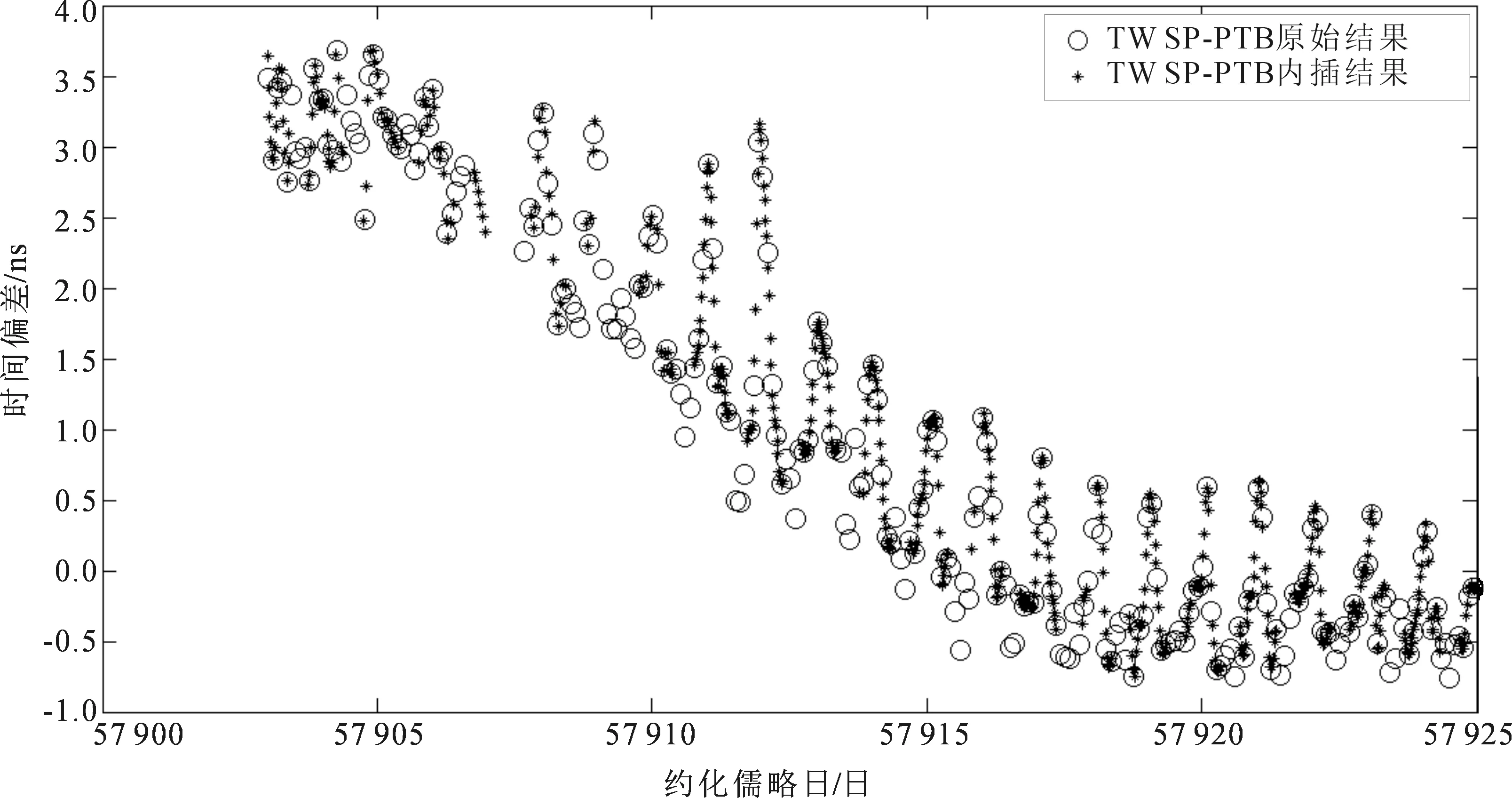
图8 SP-PTB链路的原始结果与内插结果

根据公式(4)和(5)对USNO-NTSC和SP-NTSC链路的间接时间比对结果进行解算,并采用GPS精密单点定位时间比对的结果对上述结果进行验证评估,两种方法的比对结果如图9和图10所示。图9为USNO-NTSC链路分别采用GPS PPP和间接TWSTFT计算结果,图10为SP-NTSC链路分别采用GPS PPP和间接TWSTFT计算结果。实点为GPS PPP计算结果,菱形为间接TWSTFT计算结果。

由于各直接双向时间比对链路相互独立,所以根据各不确定度的分量得到总不确定度为：

(7)

式(7)中,u为总不确定度,ui为各直接链路的不确定度,包含uA和uB。根据式(7)由BIPM的T公报(Circular T)公布的直接链路不确定度进行的间接链路不确定度预算结果参见表2,USNO-NTSC间接链路的预算不确定度为1.89 ns,SP-NTSC间接链路的预算不确定度为1.75 ns。

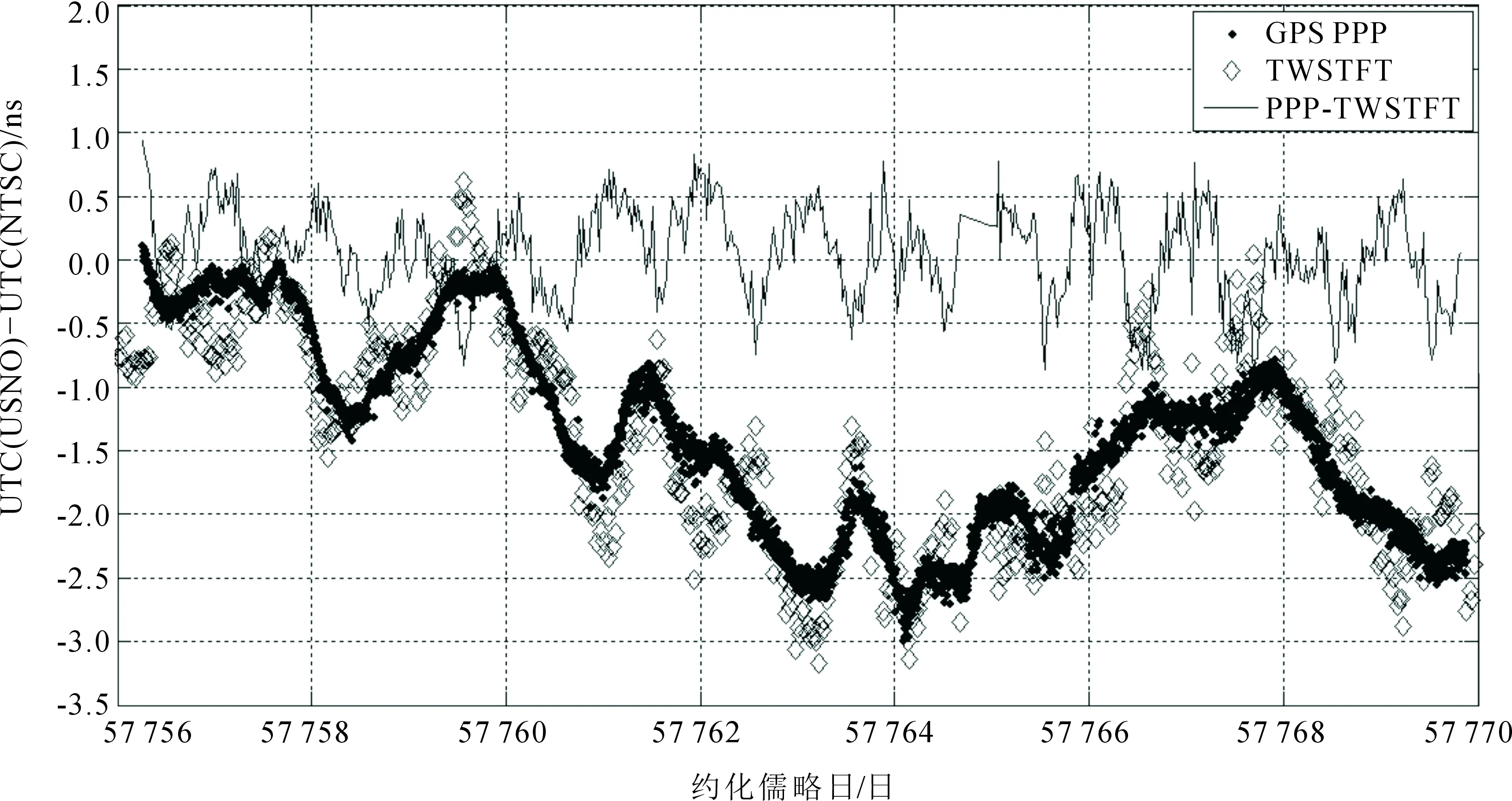
图9 USNO-NTSC的GPS PPP和间接TWSTFT时间比对结果

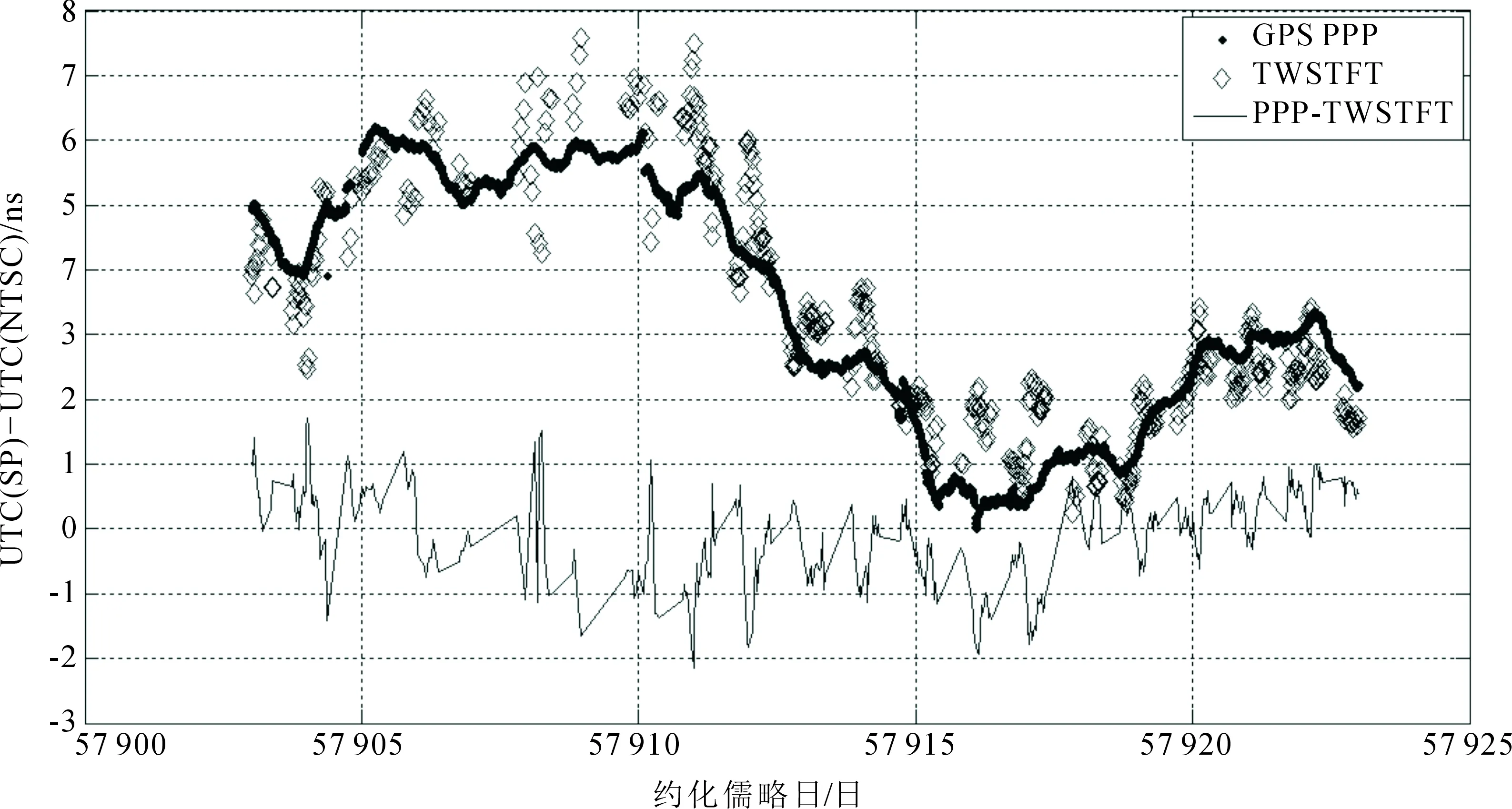
图10 SP-NTSC的GPS PPP和间接TWSTFT时间比对结果

链路uA/nsuB/nsu/nsNTSCPTB0.501.501.58USNOPTB0.301.001.04USNONTSC0.581.801.89链路uA/nsuB/nsu/nsNTSCPTB0.301.501.53SPPTB0.300.800.85SPNTSC0.421.701.75

目前BIPM校准的GPS PPP链路的不确定度为1.7 ns,由图9和图10并结合表2可知,间接链路计算的TWSTFT结果与直接链路计算的GPS PPP结果基本一致。GPS PPP与TWSTFT结果的差分别在2.54 ns和2.44 ns的不确定度范围内。

图11和图12分别为USNO-NTSC链路和SP-NTSC链路的修正Allan方差。从图11和图12可以看出,2条链路的间接TWSTFT结果的频率不确定度分别约为6×10-15(1 d)和1×10-14(1 d),符合当前卫星双向时间比对的精度要求。

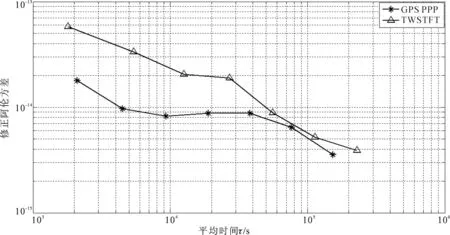
图11 USNO-NTSC链路的稳定度

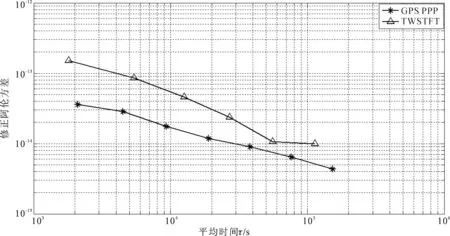
图12 SP-NTSC链路的稳定度

4 结语

采用基于中继站的方法,间接实现了超长基线的卫星双向时间比对。实验分别利用15 d和20 d的数据完成了NTSC-USNO和NTSC-SP 2条链路的间接卫星双向时间比对,并将计算结果与GPS PPP时间比对的结果进行了比较。结果表明,基于中继站的TWSTFT与GPS PPP时间比对结果基本一致,其间接链路的总时间不确定度分别为1.89 ns和1.75 ns,频率不确定度为6×10-15(1 d)和1×10-14(1 d),符合当前国际时间比对的精度要求。该方法突破了基线长度的限制,对于距离较远无法进行直接链路比对的两个实验室之间实现卫星双向时间比对有一定的借鉴意义,为将来间接TWSTFT正式用于UTC的计算提供了技术参考。