铯原子喷泉钟二阶塞曼频移的测量方法及实验

王心亮,刘丹丹,阮军,管勇,林睿,张辉,陈江,余凤翔,施俊如,张首刚

(1.中国科学院 国家授时中心,西安 710600；2.中国科学院 时间频率基准重点实验室,西安 710600;3.中国科学院大学,北京 100049)

0 引言

铯原子喷泉钟是现今时间频率计量的基准,在时间保持和计量、基础物理等领域有着广泛的应用[1-3]。作为基准频标,铯原子喷泉钟需要通过自我评定的方式获得频率不确定度。在喷泉钟的诸多频移项中,由磁场引起的二阶塞曼频移是较大的一项；同时二阶塞曼频移的测量不确定度也是限制喷泉钟不确定度降低的主要因素之一[4]。由于磁子能级︱3,1〉-︱4,1〉跃迁对磁场的敏感程度是︱3,0〉-︱4,0〉跃迁的108倍,所以二阶塞曼频移的测量是通过测量铯原子︱4,1〉-︱3,1〉Ramsey跃迁的中心频率,进而应用Breit-Rabi公式计算获得。然而Ramsey条纹反映的是原子整个运行路径上的磁场,如果喷泉钟微波激励区及自由飞行区的磁场均匀性太差,实验上就观测不到︱4,1〉-︱3,1〉跃迁的Ramsey条纹。测量磁场的另外一种常用方法是低频跃迁法,它是通过测量︱4,0〉-︱4,1〉或︱3,0〉-︱3,1〉的跃迁频率来计算原子团所在位置的点磁场(3 mm范围磁场的平均值)。该方法不受磁场均匀性的影响,而且对磁场的测量周期较短,结合飞行时间信号可以方便地对C场进行调节和补偿。本文中,我们首先应用低频跃迁的方法测出了谐振腔上方45 cm范围内的磁场分布,通过调节C场线圈电流及C场补偿线圈电流使磁场起伏最优从而获得Ramsey条纹,再应用传统的Ramsey跃迁的方法测量二阶塞曼频移及其不确定度。

1 铯原子喷泉钟二阶塞曼频移的理论研究

在磁场B的作用下,铯原子基态超精细结构塞曼子能级之间的跃迁频率由Breit-Rabi公式表示为[4]

(1)

式(1)中,υ0是基态二能级微波跃迁的标准频率,x=(gJ-gI)μBB/hυ0是无量纲磁场因数,F是总角动量量子数,F=3和4表示铯原子基态的两个超精细能级,mF是磁量子数,mF=F,F-1,…,-F。gJ=2.002 540,gI=0.401 3×10-3,是铯原子基态的朗德因子,μB是玻尔磁子,h是普朗克常数,对于(0,0)跃迁,则有：

υ(F=3,mF=0)⟺(F=4,mF=0)=υ0+427.44×108B2,

(2)

B的单位是T,式(2)中等号右边即是二阶塞曼频移。由于原子运行的整个路径上磁场是不均匀的,原子运行过程中感受到的磁场为[5]

〈B2〉=〈B〉2+σ2,

(3)

式(3)中,〈〉表示对原子运行路径上磁场的加权平均,权重大小由原子团的抛射高度和原子团经过点磁场的时间决定。σ2描述了原子运行路径上磁场的不均匀性[6]。因此铯原子喷泉钟的二阶塞曼频移可以表示为

Δυ2ndZeeman=427.44×108〈B2〉=427.44×108(〈B〉2+σ2)。

(4)

由式(1)可得︱3,1〉—︱4,1〉跃迁的频率为

υ(F=3,mF=1)⟺(F=4,mF=1)=υ0+700.83×107〈B〉,

(5)

定义fz为︱3,1〉—︱4,1〉跃迁与︱3,0〉—︱4,0〉跃迁的频率差：

(6)

磁场随时间的变化引起的不确定度可以表示为

(7)

式(7)中,fz可以通过测量喷泉钟运行时原子团最高点︱3,1〉-︱4,1〉Ramsey跃迁的中心频率获得。

对于同一超精细能级中,不同塞曼子能级的跃迁频率表示为:

υ(3,m2)↔(3,m1)=350 975×104B-13.358×108(2m1-1)B2,

(8)

υ(4,m2)↔(4,m1)=349 859×104B-13.358×108(2m1+1)B2,

(9)

式(8)和(9)中,m2代表高能态磁量子数,m1代表低能态磁量子数,所以原子运行路径上的磁场也可以通过测量︱3,0〉-︱3,1〉或︱4,0〉-︱4,1〉跃迁的频率再应用(8)、(9)两式计算获得。(8)、(9)两式是低频跃迁法测量磁场的理论依据。

2 铯原子喷泉钟工作原理

喷泉钟的光学系统与控制系统可以参考文献[7]和[8],铯原子喷泉钟的物理系统如图1所示,约3 g单质铯原子储存在铜质的铯炉中,铯炉通过真空角阀与二维磁光阱(2D-MOT)真空腔体相连,室温下铯原子自由运动进入二维磁光阱,对应最可几速度为200 m/s。二维磁光阱的作用使铯原子形成沿水平方向的慢速原子束并注入三维磁光阱(3D-MOT)。在六束冷却光与空间梯度磁场的共同作用下,铯原子被囚禁于磁光阱中心位置。磁光阱俘获原子数为108个,原子团的高斯直径为4.5 mm。计算机控制冷却光的参数实现冷原子黏团的上抛和偏振梯度冷却。原子团上抛进入选态腔,参与钟跃迁的纯态原子被挑选出来。选态后的原子上行、回落两次通过谐振腔并与微波场作用完成一次激励过程。回落的原子经过荧光探测区,通过双能级探测获得归一化的跃迁概率。方波调制馈入谐振腔的微波频率并采集跃迁概率。两次跃迁概率的差值作为误差反馈控制本地晶体振荡器完成喷泉钟的闭环运行。

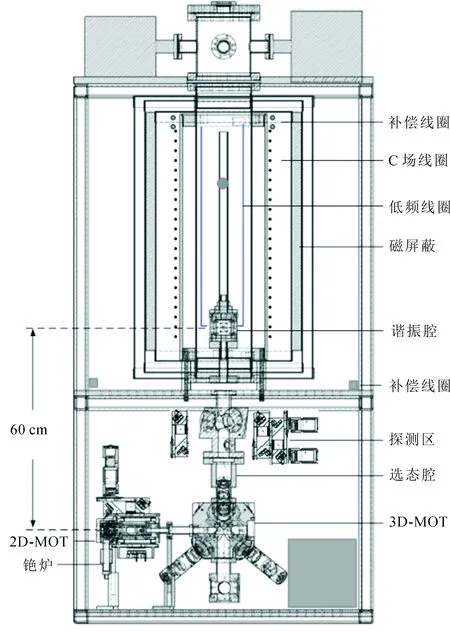
图1 铯原子喷泉钟物理系统

在喷泉管侧面设置一矩形线圈并通入低频正弦电流用于激发铯原子基态塞曼子能级之间的跃迁,跃迁概率同样通过双能级探测获得。谐振腔外围设置C场螺线管,线圈通电360 μA,产生C场强度约为110 nT。C场螺线管外覆盖3层磁屏蔽,磁屏蔽因子大于10 000。为延长C场的均匀区长度分别在C场螺线管的上端设置两个圆形补偿线圈,在C场线圈下端设计一个方形补偿线圈。调整3个线圈的电流可以使48 cm内的磁场起伏优于2 nT[9]。

3 二阶塞曼频移的测量方法及测量结果

传统评定二阶塞曼频移的方法是能够测量并跟踪记录(1,1)Ramsey跃迁的中心频率,然而(1,1)Ramsey跃迁对原子飞行路径上磁场的空间均匀性要求较高,如果磁场起伏太大,实验上将观测不到(1,1)跃迁的Ramsey条纹。喷泉钟物理系统装配阶段要求实验测量含磁屏蔽状态下谐振腔及自由飞行区C场的起伏优于2 nT。但是,当喷泉钟闭环运行以后,由于二维磁光阱磁场、三维磁光阱磁场、地磁补偿磁场等磁场的引入以及电流源的不可控变化,实验上没有观测到(1,1)跃迁的Ramsey条纹。我们首先选用低频跃迁法对原子飞行区的磁场分布进行测量和优化。当磁场分布符合要求以后再用Ramsey跃迁方法评定二阶塞曼频移。

3.1 低频跃迁方法优化原子飞行区磁场分布

对于喷泉钟系统,低频跃迁的方法即可以测量谐振腔以上自由飞行区的磁场也可以测量谐振腔内部的磁场,只是在时序控制与微波腔的应用上有所不同。测量自由飞行区的磁场时,选态腔馈入微波频率对应︱3,0〉-︱4,0〉跃迁,微波功率对应“π脉冲”,谐振腔馈入微波频率对应︱3,0〉-︱4,0〉跃迁,微波功率对应“π脉冲”。原子团上抛以后,原子布居在︱F=4〉态上,经过选态腔,︱3,0〉态的原子被选出,︱3,0〉态的原子上行经过谐振腔变为︱4,0〉态。如果在自由飞行过程中没有与低频脉冲作用,原子回落再次经过谐振腔︱4,0〉态原子再次变回︱3,0〉态,此时双能级探测︱3〉态原子数最多,︱4〉态原子数为0。如果原子在自由飞行的过程中与低频脉冲发生作用,︱4,0〉态的原子被激发到︱4,mF≠0〉态上,原子回落经过谐振腔,剩余︱4,0〉态原子变回︱3,0〉态,︱4,mF≠0〉态原子不发生改变,这样在探测区既能探测到︱3〉态原子,也能探测到︱4〉态原子。改变低频脉冲的频率,采集飞行时间信号,可以获得归一化的跃迁曲线,拟和得出低频跃迁概率最大对应的电磁场的频率,进而通过式(9)得到对应的磁场。实验中冷却光的频率每次改变0.02 MHz,对应原子团每次升高约1 cm,只在原子团运行到最高点时打开低频脉冲,脉冲时间50 ms,原子团在脉冲时间内移动3 mm,所以低频跃迁法测量得到的磁场值是3 mm内的平均值。图2是典型的低频跃迁概率曲线,拟和得到最大跃迁概率对应的频率值是387.14 Hz,对应磁场为110.6 nT。测量谐振腔内的磁场时,谐振腔一开始不通微波,︱3,0〉原子先与低频电磁场作用被激发到︱3,mF≠0〉态,当原子团将要下行飞出谐振腔时,谐振腔通入π微波脉冲,脉冲时间5 ms,将剩余︱3,0〉原子激发到︱4,0〉态。进行归一化探测,拟和得出原子跃迁概率最大点对应的低频电磁场的频率由式(8)得到对应的磁场。

应用低频脉冲测得谐振腔及自由飞行区的磁场如图3所示。圆点表示只有C场打开时的磁场分布。磁场均匀性较差,谐振腔以上45 cm范围内磁场起伏超过80 nT。打开3个补偿线圈,仔细调整补偿线圈的电流,同时用低频跃迁法测量谐振腔、喷泉管中心和喷泉管顶端3个位置上的磁场大小,使3个位置的磁场大小尽量接近,这样可以将磁场的均匀性调整到比较好的状态。图3方点表示补偿以后磁场的分布,谐振腔以上42 cm范围内磁场变化小于4 nT。实验表明,只要磁场变化优于4 nT就可以在全程观测到(1,1)跃迁的Ramsey条纹。

3.2 Ramsey跃迁的方法评定二阶塞曼频移

由于(1,1)跃迁对磁场的敏感程度是(0,0)跃迁的108倍,(1,1)跃迁的Ramsey条纹不像(0,0)跃迁那样对称和平滑,寻找中心条纹比较困难[8]。实验上常用的方法是降低原子团的上抛高度,把只有一个条纹的位置作为测量起点,这唯一的条纹就是中心条纹,缓慢增加上抛高度,可以观测到中心条纹的移动和新条纹的产生,由于高度较低时相临条纹间距较大(约6 Hz),很容易判断中心条纹的移动方向。增加上抛高度,持续采集中心条纹一直到最高点。记录每一点中心条纹对应的微波频率,便可通过反卷积求得每一点的磁场[6],应用式(6)可以得到二阶塞曼频移。

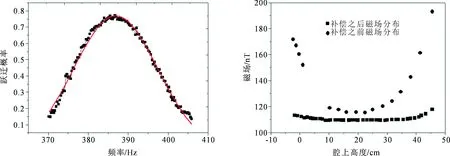
图2 低频脉冲跃迁概率 图3 原子自由飞行区磁场分布

图4为原子团经过谐振腔最初两个点的Ramsey条纹,方点是腔上第1个点的Ramsey条纹,条纹只有一个峰,三角点是第2个点的条纹,有两个峰,比较两个条纹可以判断中心条纹的位置。图5是谐振腔以上不同高度Ramsey跃迁中心条纹所对应的频率,上下两条曲线是中心条纹相临两条条纹的情况,高度变化引起的中心条纹移动始终小于与其相临两条条纹的间距,中心条纹在连续采集过程中没有出现错误。

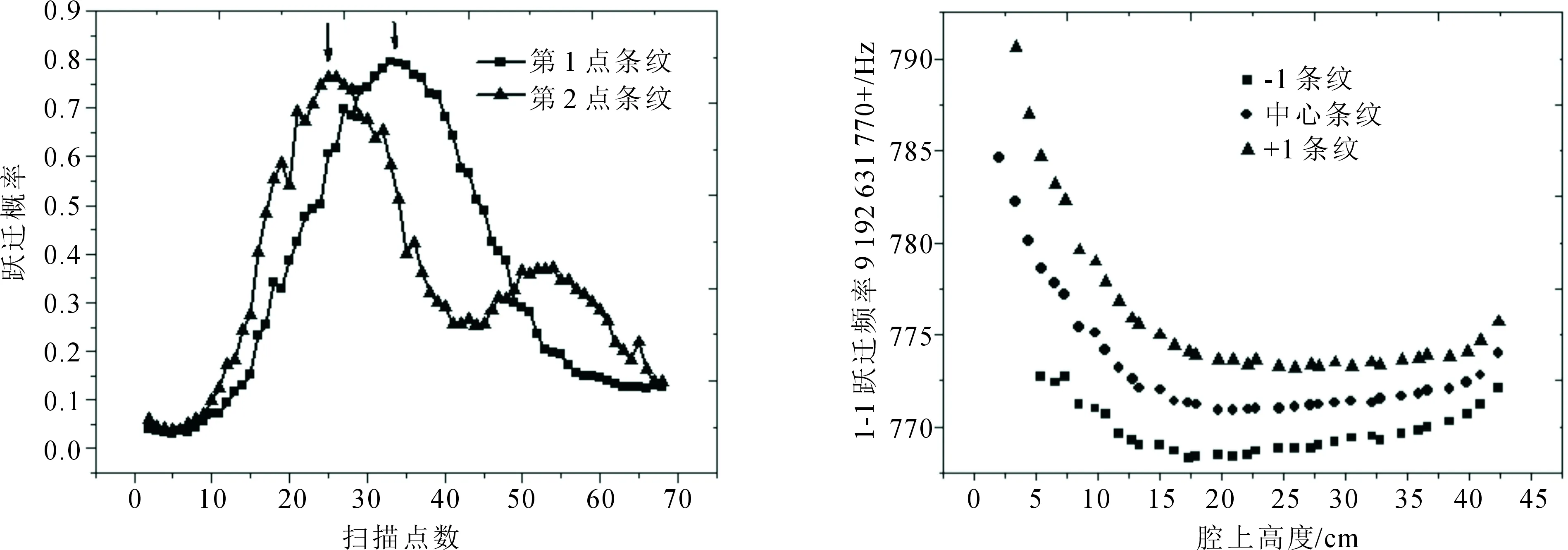
图4 谐振腔上方最初两条条纹 图5 连续采集中心3条条纹的跃迁频率

图6是根据Ramsey条纹的中心频率反卷积求出的谐振腔上方的磁场分布,这个结果与低频脉冲测得的磁场基本一致,但测量精度更高。受磁场均匀性和喷泉钟信噪比的限制,当原子团运行到谐振腔上方42 cm时,Ramsey条纹消失,所以实验系统中Ramsey方法只能测量谐振腔上方42 cm之内的磁场。图7是铯原子喷泉钟常规运行高度处(1,1)跃迁的Ramsey条纹,中心条纹对应fz=773 Hz。由式(6)求得二阶塞曼频移量是56.57×10-15,由图6的磁场分布求得σ2=0.333×10-18T2,由C场的空间不均匀性引起的频率不确定度为1.55×10-18,二阶塞曼频移的测量不确定度主要源自C场随时间的变化。将喷泉钟锁定在(1,1)跃迁的中心频率上记录频率的变化δfz可以获得C场随时间的变化引起的不确定度。

图(8)是以氢钟为参考,记录(1,1)跃迁的中心频率3 d内的变化,由式(7)可得二阶塞曼频移的相对不确定度为2.93×10-16。

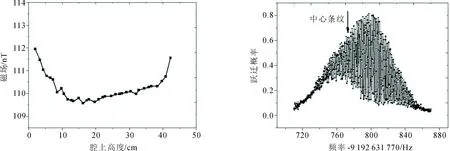
图6 原子自由飞行区磁场分布 图7 (1,1)跃迁的Ramsey条纹

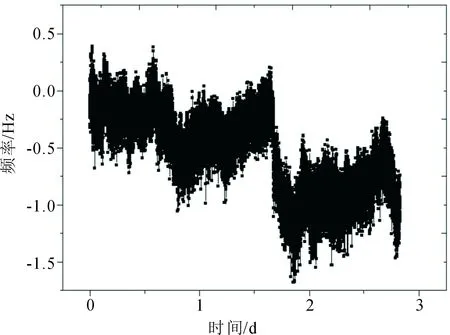
图8 (1,1)跃迁中心频率的变化

4 结论

二阶塞曼频移的测量不确定度是限制铯原子喷泉钟不确定度提高的主要因素之一,本文应用低频跃迁的方法测量并优化了原子运行路径上磁场的分布,采用Ramsey跃迁方法获得了二阶塞曼频移的频移量和不确定度。受C场电流源稳定性和磁屏蔽性能的影响,二阶塞曼频移的测量不确定度较大。下一步改进重点是更换稳定性较好的C场电流源,提高磁屏蔽的性能,以降低二阶塞曼频移的测量不确定度。