考虑速度约束的无人机Dubins路径规划*

刘 流，梁晓龙，何吕龙，朱创创

（空军工程大学空管领航学院，西安 710051）

0 引言

随着无人机的飞速发展，及其应用越来越广泛，无人机的路径规划问题也受到了广泛关注。为无人机设计可飞性高的飞行路径并对无人机实施有效控制，对于无人机的编队构成和保持具有重要意义[1-4]。

当前无人机路径规划技术多从地面机器人领域借鉴而来，并未较好考虑无人机的性能约束，常规的解决办法是先由路径规划算法生成一系列直线段连接的路径，随后进行光滑处理得到可飞路径。Dubins[5]考虑到了转弯半径对于车辆（飞行器）运动的影响，使用几何方法首先讨论了运动初始状态和终止状态之间的最短曲线问题，并在1957年给出了相应数学证明。梁勇等[6]将Dubins路径应用到了导弹的时间与角度控制中，利用Dubins路径转弯特性完成角度控制，采用微调转弯半径的方法实现了精确时间控制；关震宇等[7]则基于Dubins路径提出了无人机的避撞规划算法，首先分析了单障碍模型，并利用遗传算法推广到了多障碍情况中，实现了无人机的实时避撞。Yeol J W等[8]提出了基于Dubins路径获取二维最短路径的方法；Shanmugavel[9]基于Dubins路径提出了多无人机协同路径产生的方法，并利用Clothoid曲线有效解决了Dubins路径曲率不连续的问题。

目前针对二维、三维空间内的基于Dubins路径的路径规划研究较多，能够实现无人机以期望速度方向及最短路径到达指定位姿点，但并未考虑无人机在运动过程中的速度大小问题，以一定的速度大小到达位姿点对于无人机编队队形的保持以及后续任务的执行具有重要意义，无需进行另外的速度大小调整，便可立即执行下一任务，提高了无人机任务执行的连续性。

1 基本问题描述

无人机执行任务的过程可看作对一系列任务点Pi（i=1，2，…，n）进行跟踪的过程[10]，本文对无人机在二维平面内，从起始点Ps（Xs，Ys）运动至终止点Pf（Xf，Yf）的过程进行分析，如图1所示。

图1 无人机执行任务过程

在二维坐标中，无人机的运动学模型为

2 Dubins路径概述

2.1 Dubins路径基本概念

对于无人机的控制，除路径点的坐标外，定义无人机在该点的方向也十分重要，对于无人机后续任务的执行具有重要意义。故本文中所提到的路径点均为位姿点（带有坐标与方向）。两个位姿点间的最短路径是Dubins路径[5]。Dubins路径可简单定义为，在曲率的限制下，平面内两个位姿点间的最短可行路径是CSC路径或CCC路径，或是它们的子集，其中C表示圆弧段，S表示与C相切的直线段，从Dubins路径的定义可以看出，其实质便是无人机的直线运动模型与匀速转弯运动模型的交互运动路径。根据实际任务的需要以及无人机运动性能的约束，无人机的飞行航程通常会远大于无人机的最小转弯半径，本文仅考虑CSC路径情况，即时，此时Dubins路径一定存在。

由于在给定位姿点下，无人机可以向左转弯和向右转弯，路径可以以顺时针方向（右）或以逆时针方向（左）开始或结束，此时便存在多条可飞Dubins路径，Andrei M Shkel[11]给出了最短 Dubins路径的分类结果，针对起始位姿点与终止位姿点方向角所在象限的不同，以及根据角度的具体差值确定了不同情况下的最短Dubins路径，具体过程不再赘述。

2.2 解析几何Dubins路径设计方法

本文采用解析几何方法生成Dubins路径，仅对初始位姿点与终止位姿点方向角均在第一象限的情况进行分析，其他情况下的算法可参照此情况，本文不再一一分析。文献[12]中给出了利用解析几何方法产生Dubins路径的方法，其步骤如图2所示。

图2 Dubins路径产生步骤图

首先根据起始位姿点与终止位姿点的信息以及无人机最小转弯半径确定起始、终止转弯圆圆心，随后确定起始、终止转弯圆的切点，便可得出满足条件的最短Dubins路径。

本文直接利用此方法根据初始条件产生Dubins路径，如下页图3所示。

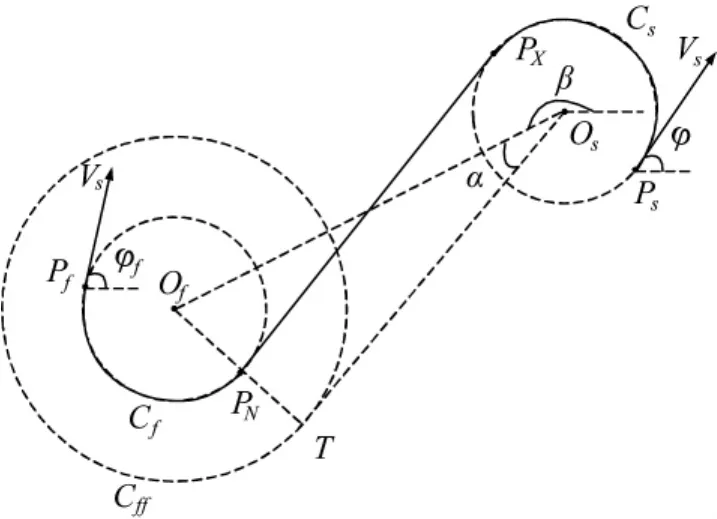
图3 Dubins路径示意图

图3中Ps（Xs，Ys）为起始位姿点，Pf（Xf，Yf）为终止位姿点，φs，φf分别是起始航向角与终止航向角，Os，Of分别是起始转弯圆与终止转弯圆的圆心，PX，PN分别是起始转弯圆与终止转弯圆的切点坐标，圆Cs，圆Cf分别为起始和终止转弯圆。文献[6]中已经证明在其他条件不变的情况下，转弯半径越小，总航程越小，故本文中取起始转弯圆和终止转弯圆半径均为 rmin，圆Cff半径为 2rmin。根据文献[11]中的结论，图4中的最短路径应为LSR，即在初始点左转弯加直线段加右转弯到达终止点。

3 速度控制算法及虚拟位姿点设置

速度控制算法基本步骤如下：

Step2计算直线PXPN段速度；

Step4根据终止点的速度大小方向要求以及无人机性能约束，确定虚拟位姿点坐标；

Step5计算虚拟位姿点至终止任务点段速度。

起始转弯圆心Os（xcs，ycs）的坐标为

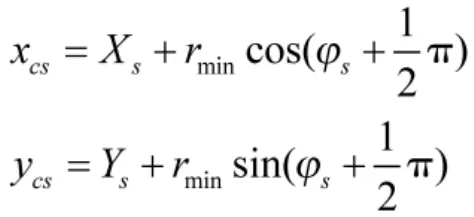
OsOf与OsT之间的夹角为

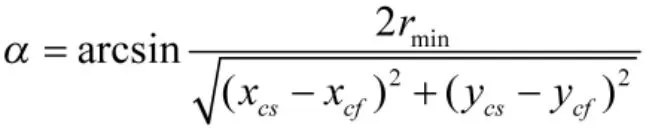
圆心中心线OsOf的斜率为tanβ

圆Cs上切出点PX的坐标为

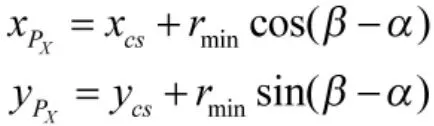
从初始点Ps转弯至切出点PX所转过的圆心角为

2）计算直线PXPN段速度

圆Cf上切入点PN的坐标

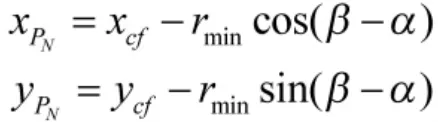
则在直线PXPN段无人机速度为

终止转弯圆心Of（xcf，ycf）的坐标

从切入点PN转弯至终止点Pf所转过的圆心角为

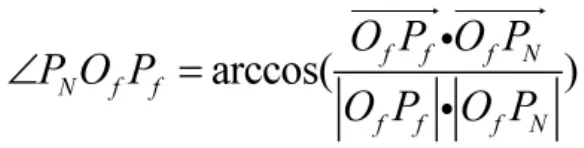
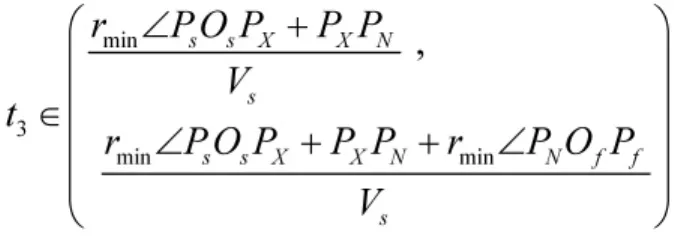
4）确定虚拟位姿点

如图4所示，无人机从起始点Ps以速度大小Vs出发，航向角为φs，现要求无人机以速度大小Vf，航向角φf到达任务点Pf，Pfx点即为所需设置的虚拟位姿点，无人机在到达Pfx点后在PfxPf段完成速度大小的调整。

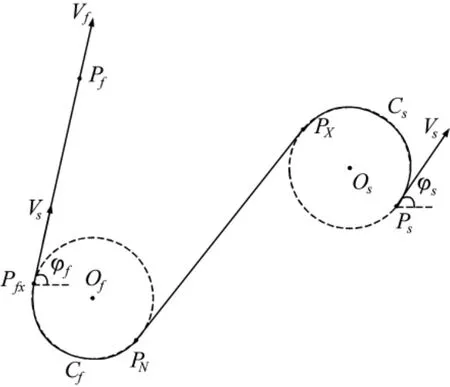
图4 虚拟位姿点设置

PfxPf段为速度调整段，所需时间为

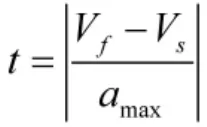
调整路程长度为

此处amax为无人机最大纵向加速度大小，为标量。

点Pfx的坐标为

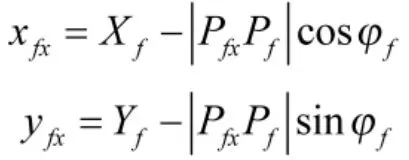
5）计算虚拟位姿点至终止点段速度

无人机的速度为

通过以上步骤便计算出在跟踪Dubins路径过程中无人机的速度，以此作为无人机的输入对其实施控制可完成对Dubins路径的有效跟踪。

4 实例仿真

4.1 Dubins路径速度控制仿真分析

现建立以（0，0）位坐标原点的平面直角坐标系，假设无人机起始位姿点坐标为（150，30）m，起始速度大小为1 m/s，方向角为30°，现要求无人机到达任务点（31.5，60）m，速度大小为 3 m/s，方向角为60°。无人机最大纵向加速度大小为0.5 m/s2，最大飞行速度为5 m/s，最小飞行速度为0.5 m/s，最小转弯半径为20 m。

根据Dubins路径的解析几何设计方法及第3节中速度算法进行模拟仿真，结果如图5所示。

图5 Dubins路径仿真图

在图5（a）中，红色箭头表示初始位姿点速度方向，黑色箭头表示终止位姿点速度方向，蓝色路径为Dubins路径，紫色直线部分为速度大小调整段，可以看出根据Dubins路径解析几何设计算法，无人机从起始点Ps生成了一条到达虚拟位姿点Pfx的最短Dubins路径，并在直线部分进行调整速度大小，最终到达终止任务点Pf。图5（b）中的蓝色虚线和红色实线分别反映的是无人机在整个运动过程中在x轴和y轴方向上的速度大小随时间的变化，由于Dubins路径匀速转弯的特性，导致速度在某些拐点处可能变化不连续，在实际中可能会出现一定的误差，其中速度曲线的首尾曲线段分别为起始、终止转弯圆弧的速度大小，直线段为切线段匀速运动，可以看出无人机始终以1 m/s的速度大小从起始位姿点运动至虚拟位姿点，随后进行速度大小的调整，最终以指定速度大小到达终止任务点Pf。

4.2 飞行实验验证

4.2.1 实验平台简介

本文采用单架四旋翼无人机作为实验平台，主要由机架、动力系统以及飞行控制核心构成的底层飞控系统和上层上位机系统、数传以及自组网模块组成，单架重量约1.5 kg，最大飞行时间约15 min。实物如下页图6所示。

图6 无人机实验平台

无人机飞控系统采用Pixhawk系统，无人机与地面站间的通信协议采用mavlink通信协议，通信天线频率为133 MHz，地面站采用联想某型笔记本电脑，使用Mission planner作为飞行参数设置的软件，同时选择Qgroundcontrol作为控制软件，根据需要实现无人机的起飞、降落。系统框图如图7所示。

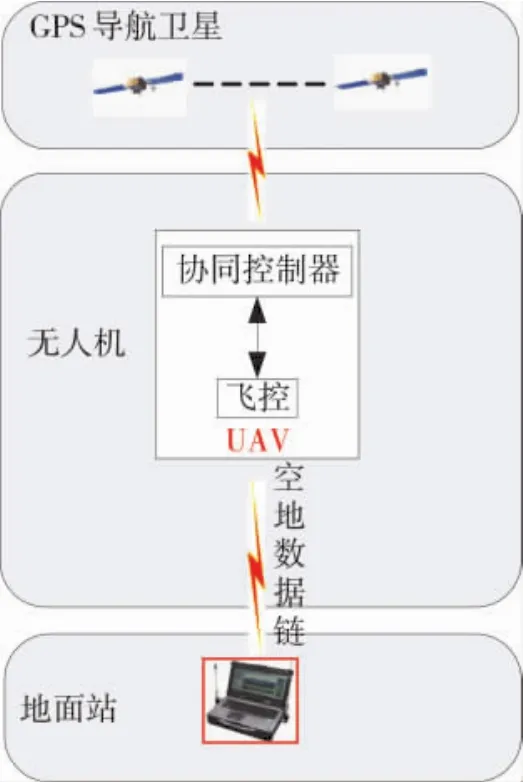
图7 实验系统示意图

4.2.2 实验结果分析

本实验采用速度作为控制变量，对无人机实施运动控制。首先生成Dubins路径并通过速度算法得出速度控制输入，通过地面站将控制指令实时发送至四旋翼无人机进行控制，同时无人机将自身速度位置信息实时回传至地面，记录实验结果如图8所示。

1）结果分析

图8（a）、（b）反映的是无人机在实验过程中在x轴及y轴方向上的速度大小对比图，蓝色曲线为实验速度记录数据，红色曲线为控制输入速度，可以看出在初始阶段无人机对于速度控制输入存在响应延迟。由于通信等原因，实验过程中接收到的无人机速度数据存在丢包情况，但可以看出在实验过程中无人机能够按照期望速度运动。图8（c）中蓝色十字轨迹为无人机在实验过程中的飞行轨迹，红色曲线为期望Dubins路径，从实验过程中无人机的飞行轨迹可以看出实验飞行轨迹与期望轨迹存在一定的误差。图8（d）中为实验轨迹与期望轨迹的误差变化曲线，由于无人机初始阶段的响应延迟，误差在初始阶段快速增长，随后在一定范围内波动。

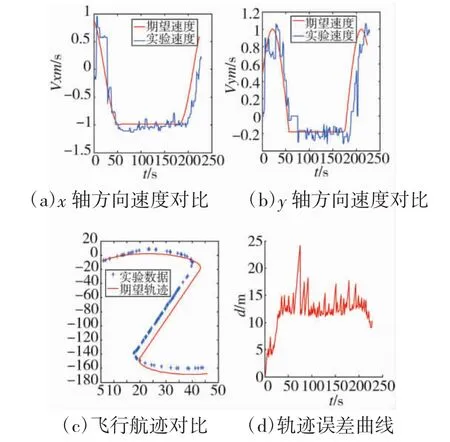
图8 实验结果分析图

2）误差分析

从速度对比曲线可以看出，在实验开始阶段的10 s时间内，无人机并未立即达到期望的速度，出现初始速度上的响应延迟，导致无人机在后续飞行过程中始终存在一定误差。从轨迹误差曲线也可以看出，在初始阶段，由于无人机的响应延迟，误差快速增长，在后续过程中，虽然由于GPS定位设备的误差原因导致误差仍存在一定的波动，但总体保持在一定范围内，实现了有效的控制。

3）解决方法

针对无人机初始阶段的响应延迟，可以采取为无人机设置一段响应缓冲路径，待无人机完成速度的调整，能够稳定地响应控制输入后，方可按照所提出的速度控制方法对无人机实施有效控制。

5 结论

针对无人机的运动性能约束，本文选择Dubins路径作为无人机飞行路径，利用了Dubins路径可飞性高和二维平面内路程最短的特点，对于无人机的运动控制采取了速度控制的方法，提出了Dubins路径的速度算法，计算出无人机的飞行速度作为控制输入，通过设置虚拟位姿点使无人机能够完成速度大小的调整，按照指定速度大小到达任务点。飞行实验结果表明采用Dubins路径作为无人机的飞行路径是简便可行的，同时速度控制方法能够对无人机进行有效控制。在下一步的研究工作中，将把Dubins路径应用到无人机群的编队构成、重构等方面中，更好地实现无人机群编队控制。