儿童数学抽象力形成的教学分析与提升策略

孙欣 王乃涛

【摘 要】数学抽象力是儿童数学学习的必备品质。儿童的数学抽象学习具有表达直接性、表征直观性、原理探究性、思维半逻辑性等特点，教师应注重建构有助于提升儿童数学抽象力的适性场域——匹配抽象内容的适应场、激活抽象方法的运用场、提升高阶思维的层次场。

【关键词】数学抽象力;教学分析;提升策略;抽象内容;抽象方法;高阶思维

【中图分类号】G623.5  【文献标志码】A  【文章编号】1005-6009（2019）89-0033-04

【作者简介】1.孙欣，江苏省淮阴师范学院第一附属小学（江苏淮安，223001）课程教学部副主任，一级教师，淮安市数学学科带头人;2.王乃涛，江苏省淮安经济技术开发区教师发展中心（江苏淮安，223005）数学教研员，高级教师，江苏省数学特级教师。

史宁中教授曾指出：人的基本思維能力就是想象能力和抽象能力，其他思维能力都是它们派生的。数学抽象最能体现数学本质。

一、儿童数学抽象力形成的困惑

（一）对原初概念表征不清，抽象过程缺少思维基础

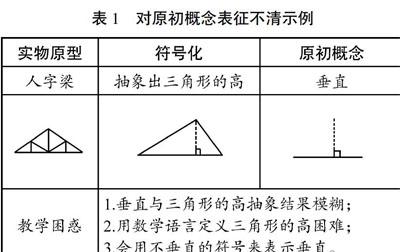
我们通常用已知概念（原初概念）来定义新概念，如用因数来定义质数、合数，用自然数来定义因数。学生对原初概念的理解直接影响他们的新概念形成。如学习苏教版四下《三角形的高》一课时，由于学生对原初概念的表征与理解不清，往往会致使其新概念抽象过程模糊（如表1）。

（二）对问题解决机械模仿，抽象方法选择运用不当

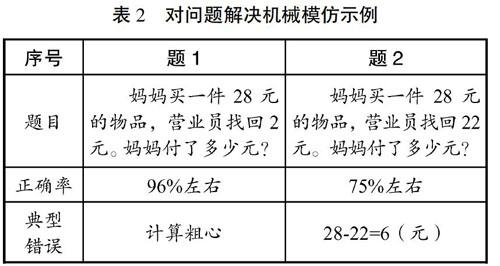
教师常结合生活情境来帮助学生理解数学问题，以培养他们用数学的眼光观察生活的能力。但是，如果教学浮于表面，学生则会对方法理解不透、运用不当。如学习苏教版一下《100以内加减法》一课时，常常会出现如下页表2所示的问题。两道题题型相同，正确率却相差较大。题1找回钱数很少，符合生活中找回钱少的现实暗示，学生会根据数据特点机械模仿解决题1的方法来解决题2。

（三）对数学原理表达不清，抽象结论难以语义说明

学数学需探究数学原理。建构数学原理时，可举例、归纳、概括，也可以纯数学逻辑推导。受认知能力限制，学生表达数学原理时往往会出现不全面、不完整、不准确等情况。如教学苏教版五下《分数的基本性质》一课，在折纸、填等式、发现分子分母倍数关系等环节，学生能轻松应对，但让他们用语言概括规律时，他们的表达却往往不如人意，有的只表达出了乘或除中的一种情况，有的考虑不到0除外。

（四）对数学本质把握不准，核心要素难以深刻辨析

同一对象可用不同标准进行分类。同一概念处于不同上位概念之下，也以不同树状结构引发下位概念。学生对交叉状的概念体系结构往往难以辨别。如教学苏教版五下《因数与倍数》一课，不等于0的自然数可分为1、质数和合数，也可分为奇数和偶数。但因学生对数学概念的核心要素把握不准，导致他们对两种分类标准（是否2的倍数，因数有多少）和概念结构难以深入辨析。

二、儿童数学抽象力的含义及学习特征

（一）儿童数学抽象力的含义

数学抽象力是在数学抽象过程中形成的理解力、判断力、想象力、概括力等能力的总和。

（二）儿童数学抽象学习的典型特征

小学生的数学抽象主要指情境性抽象或经验性抽象，具有两重性，既表示从情境中提取的过程，又表示从过程中得出的经验概念。

1.表达的直接性。儿童头脑中的信息属于“自然结构”，加工起来相对困难，难以进行数学逻辑解释，而是一点一点地直接表达想法。

2.表征的直观性。儿童表征数学概念从实物、图形开始，尚不能完全脱离数学原型展开逻辑思考，抽象过程以具体形象和表象为支撑。

3.原理的探究性。儿童不满足于接受现有的结论，喜欢从数学事实出发猜想、追问、寻找数学规律，具有一定的探究意识与能力。

4.思维的半逻辑性。儿童抽象能力的发展介于实物、图形的形象认知和原理、规律的抽象过程之间，具有一定的但不完全的逻辑性，我们称为“半逻辑性”的学习特点。

三、儿童数学抽象力的培养策略

（一）全面打破——匹配抽象内容的适应场

数学抽象主要有概念抽象、规律抽象、运算抽象、关系抽象、思想方法抽象等。

1.概念抽象——去异求同，抽离本质属性。要促进学生建立数学概念，教师应注重引导学生观察、比较，区别事物的本质属性与非本质属性，发现事物间共同的属性，形成正确的概念。如教学苏教版二下《认识角》一课，可出示实物图片，引导学生描出图片中的角，从实物图中剥离出角的平面图形，再通过观察、比较抽象出平面图形的共同特点，抽离出角的本质属性（由一个顶点和两条边组成）。

2.规律抽象——去粗取精，概括临近结论。在规律探究中，学生根据研究素材形成的发现有些无普适性。教师应引导学生去除外在表象，展示本质，在临近结论的基础上形成正确的结论。如教学苏教版四下《多边形内角和》一课，学生通过量、算、拼等方法得出了三角形与四边形的内角和及2倍关系，但还不能发现边数与内角和的关系。教师适时启发：想象一下，多边形的内角和会与什么有关？当学生理解了多边形内角和与三角形内角和有关时，就容易找到研究五、六边形内角和的方法了。借助图形直观进行归纳推理，解释规律的合理性，有助于学生矫正其临近结论。

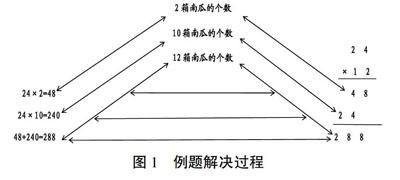
3.运算抽象——理法相通，提炼运算法则。在计算教学中，沟通算理与算法很重要。算理是算法的基础，及时沟通算法与算理的联系有利于算法的抽象、提炼与掌握。如苏教版三下《两位数乘两位数的笔算》一课的例题为：幼儿园购进12箱迷你南瓜，每箱24个。一共有多少个？教师教学时应注意引导学生理解算理和竖式过程（如图1），沟通新旧方法，并启发学生讨论：（1）竖式中第二步算出的积的末位为什么要与十位对齐？（2）新算法为什么要分步表示过程？在数学问题情境中沟通新旧方法，理解算理，抽象出运算法则。