1龄三角帆蚌壳形态性状对体质量的通径分析

，，，，，，，

(1.金华职业技术学院，浙江 金华 321007；2.金华市九色珍珠研究所, 浙江 金华 321017；3.金华市威旺养殖新技术有限公司，浙江 金华 321017；4.金华市水产技术推广站，浙江 金华 321017；5.绍兴文理学院 生命科学学院， 浙江 绍兴 312000)

三角帆蚌Hyriopsiscumingii隶属于蚌科Unionidae、珠蚌亚科Unioninae、帆蚌属Hyriopsis，是中国特有的淡水育珠蚌[1]。三角帆蚌以其优良的育珠性能已经替代褶纹冠蚌Cristariaplicata、背角无齿蚌Anodontawoodiana等，成为中国淡水珍珠蚌的主要品种[2]，其所产珍珠质地细腻光滑、颜色丰富多样，已经在中国大面积养殖[3-4]，同时，三角帆蚌育种研究也在逐步开展。目前，李梦军等[5]、闻海波等[6]和张元培[7]分别用群体选育、种内杂交、种间杂交等育种方法开展了三角帆蚌的育种工作，并取得重要进展。

选择育种是贝类遗传改良的重要手段。贝类各数量性状间存在遗传基础上的密切联系，相关分析和通径分析方法能够查明各数量性状间的相互关系，对选择育种具有重要的参考价值。目前，通径分析方法已经在水产贝类育种上得到了广泛应用。如刘小林等[8]运用通径分析方法分析了栉孔扇贝Chlamysfarreri贝壳尺寸性状对活体质量的影响效果。闫喜武等[9]运用通径分析方法研究了四角蛤蜊Mactraveneriformis形态性状对体质量性状的影响。刘志刚等[10]和郑怀平等[11]对华贵栉孔扇贝Chlamysnobilis产量及闭壳肌大小进行了通径分析。王辉等[12]运用通径分析方法研究了南海毛蚶Scapharcasubcrenata形态特征对体质量的影响。除上述几种贝类外，通径分析方法还应用到了紫石房蛤Saxidomuspurpuratus[13]、中国蛤蜊Mactrachinensis[14]、菲律宾蛤仔Ruditapesphilippinarum[15]、魁蚶Scapharcabroughtonii[16]等贝类的研究中。在对三角帆蚌Hyriopsiscumingii的研究中，也有学者运用通径分析方法对成蚌数量性状进行了相关分析[17-18]。但关于三角帆蚌幼蚌壳形态性状对质量性状的影响尚未见报道。本研究中，对1龄蚌4个形态性状及体质量的相关性进行了研究，对体质量进行通径分析并建立回归方程，旨在为1龄三角帆蚌幼期的选育提供数据资料和测量指标。

1 材料与方法

1.1 材料

试验用1龄三角帆蚌幼蚌来源于浙江省金华市威旺养殖新技术有限公司，为自然养殖群体的繁殖后代，养殖于试验基地的6#养殖塘。养殖密度为100只/网箱(40 cm×40 cm×12 cm)，吊养深度为30～40 cm，按常规模式进行养殖管理。

1.2 方法

1.2.1 测量方法 幼蚌达到1龄时先随机抽取4个网箱，再从中随机抽取120只1龄蚌，将其贝壳表面的泥污清洗干净后用于测量。用游标卡尺(精确到0.02 mm)测量蚌的壳长(x1)、壳高(x2)、壳宽(x3)和全高(x4)(图1)，用电子天平(精确到0.01 mg)称量其体质量(y)。

图1 1龄三角帆蚌贝壳形态性状测量示意图Fig.1 Illustration of measurement of shell morphology of juvenile freshwater mussel Hyriopsis cumingii

1.2.2 分析方法 各性状测量数据经SPSS 21.0软件统计整理，计算平均数、标准差和变异系数，再使用软件中的K-S单样本检验(Kolomogorov-Simirnov one sample test)分析各性状的分布是否符合正态分布。然后进行各性状间表型相关分析、各形态性状对体质量的通径分析并计算决定系数。通过逐步回归法，剔除偏回归系数不显著的性状，建立最优多元回归方程，并对方程进行显著性检验。

体质量(y)的回归方程采用的线性模型[19]为

y=b0+b1x1+b2x2+…+bixi。

其中：y为因变量；b0为常数项；xi为自变量；bi为对应的偏回归系数。偏回归系数bi是有单位属性的，无法直接进行比较，因此，对bi的分子、分母分别除以y和xi的标准差，得到从自变量xi到因变量y的直接通径系数Pyi xi，即

Pyi xi=biσxi/σy。

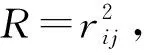
2 结果与分析

2.1 形态性状及体质量的描述统计结果

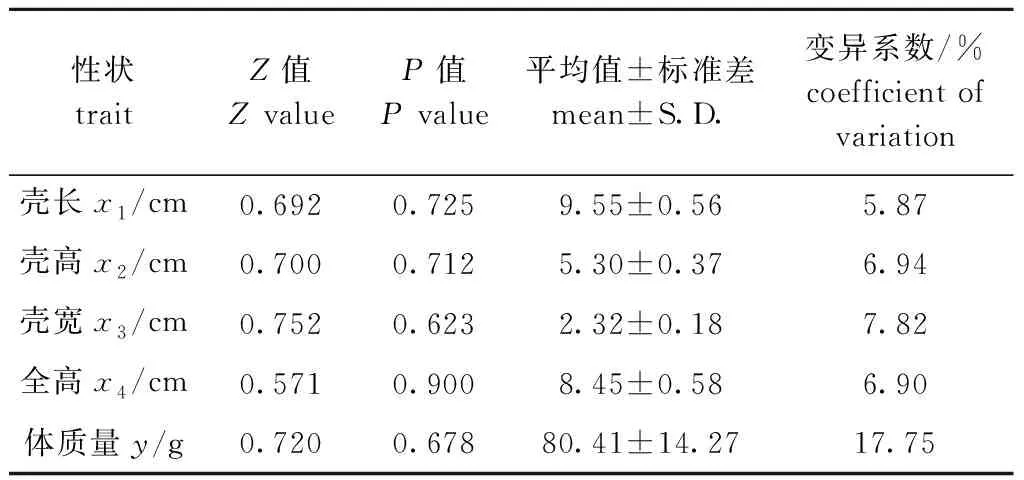
1龄三角帆蚌壳长、壳高、壳宽、全高及体质量等表型数据的描述统计结果如表1所示，在这些性状中，体质量的变异系数最大，壳长的变异系数最小。正态性K-S检验结果显示，P值均大于0.05，说明所分析性状的分布均符合正态分布，可对这些性状做进一步地通径分析。

表11龄三角帆蚌形态性状及体质量的表型统计量(n=120)

Tab.1Phenotypicstatisticsofmorphologicaltraitsandbodyweightofone-yearoldfreshwatermusselHyriopsiscumingii(n=120)

性状traitZ值Z valueP值P value平均值±标准差mean±S.D.变异系数/%coefficient of variation壳长x1/cm0.6920.7259.55±0.565.87壳高x2/cm0.7000.7125.30±0.376.94壳宽x3/cm0.7520.6232.32±0.187.82全高x4/cm0.5710.9008.45±0.586.90体质量y/g0.7200.67880.41±14.2717.75

2.2 形态性状及体质量间的相关性

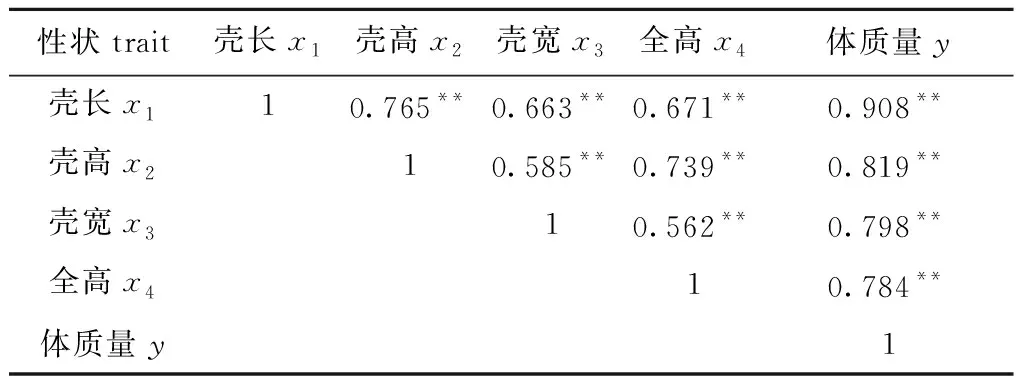
1龄三角帆蚌各性状间的表型相关系数见表2，所列各性状间的表型相关均达到了极显著水平，表明所选指标进行相关分析具有重要的实际意义。其中，体质量与壳长的相关性最强，相关系数为0.908，壳宽与全高的相关性最弱，相关系数为0.562。

表21龄三角帆蚌各性状间的表型相关系数

Tab.2Phenotypiccorrelationcoefficientsbetweenobservedtraitsofone-yearoldfreshwatermusselHyriopsiscumingii

性状trait壳长x1壳高x2壳宽x3全高x4体质量y壳长x110.765**0.663**0.671**0.908**壳高x210.585**0.739**0.819**壳宽x310.562**0.798**全高x410.784**体质量y1

注：** 表示在 0.01 水平(双侧)上显著相关

Note: **, significant correlation in 0.01 level

2.3 形态性状对体质量的通径分析

根据通径分析的原理，将壳长、壳高、壳宽与全高对体质量的影响效应剖分为直接作用Pi(即通径)和间接影响两部分，剖分结果见表3。从表3可见：壳长、壳宽与全高对体质量的直接作用均达到极显著水平(P<0.01)，壳高对体质量的直接作用达到显著水平(P<0.05)，均具有统计学意义；壳长对体质量的直接作用最大，达到0.479，直接作用大于间接影响，是影响体质量的最主要因素。而壳高、壳宽、全高对体质量的间接影响均大于各自的直接作用，且这种间接影响效应主要是通过影响壳长而产生的。

表3 1龄三角帆蚌形态性状对体质量影响的通径分析Tab.3 Path analysis of morphological traits on body weight of one-year old freshwater mussel Hyriopsis cumingii

注：* 为显著相关(P<0.05)，** 为极显著相关(P<0.01)

Note: *,significant correlation(P<0.05); **,very significant correlation(P<0.01)

2.4 形态性状对体质量的决定程度

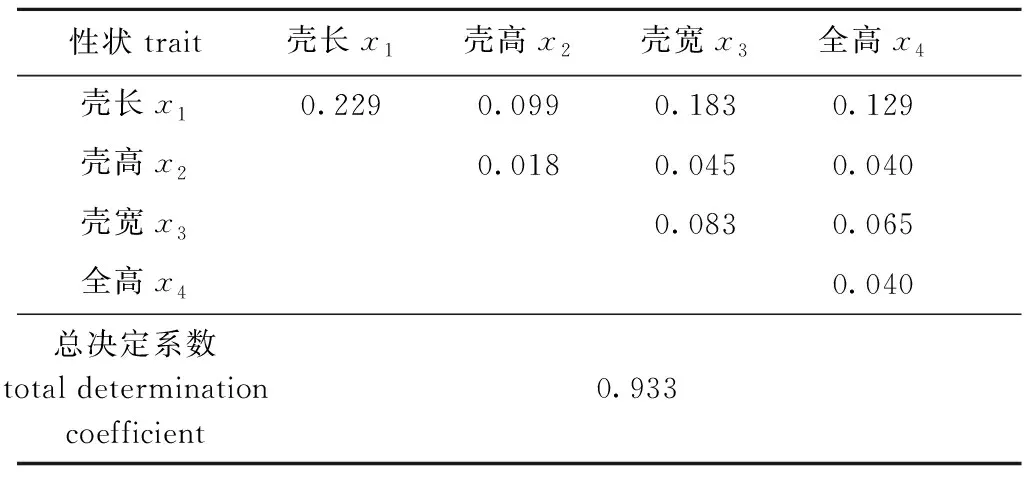
各形态性状及它们协同对体质量的决定系数如表4所示，其中,对角线上给出了每个形态性状单独对体质量的决定系数，对角线以上给出间接决定系数。总的决定系数为0.933，它与相关指数R2的数值相等，表明本研究中所列形态性状是影响体质量的重点性状，其他形状影响相对较小，仅有0.067。各性状中，壳长对体质量的直接决定程度最大，达到22.9%，壳长与壳宽的共同决定程度最大，达到18.3%。

表41龄三角帆蚌形态性状对体质量的决定系数

Tab.4Determinationcoefficientsofmorphologicaltraitsonbodyweightofone-yearoldfreshwatermusselHyriopsiscumingii

性状trait壳长x1壳高x2壳宽x3全高x4壳长x10.2290.0990.1830.129壳高x20.0180.0450.040壳宽x30.0830.065全高x40.040总决定系数total determination coefficient0.933

2.5 最优回归方程的建立

运用逐步回归方法建立形态性状对体质量的最优回归方程为

y=-157.919+12.195x1+5.266x2+22.613x3+4.920x4。

其中：y为体质量(g)；x1为壳长(cm)；x2为壳高(cm)；x3为壳宽(cm)；x4为全高(cm)。

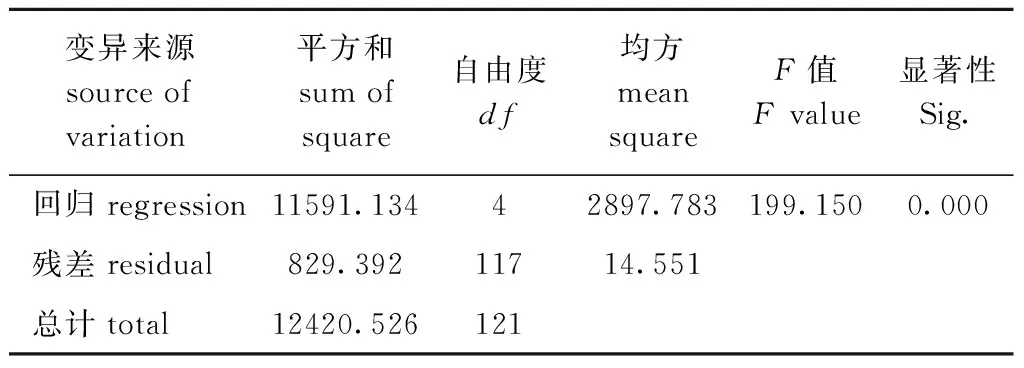
多元回归关系的显著性检验(表5)和各形状偏回归系数的显著性检验(表6)表明，方程的回归关系达到极显著水平(P<0.01)，壳长(x1)、壳宽(x3)与全高(x4)的偏回归系数达到极显著水平(P<0.01)，壳高(x2)的偏回归系数达到显著水平(P<0.05)。

表51龄三角帆蚌体质量多元回归关系的方差分析

Tab.5ANOVAformultipleregressionofone-yearoldfreshwatermusselHyriopsiscumingii

变异来源 source of variation平方和 sum of square自由度df均方 mean squareF值F value显著性 Sig.回归regression11591.13442897.783199.1500.000残差residual829.39211714.551总计total12420.526121

表61龄三角帆蚌各性状偏回归系数的显著性检验

Tab.6Testofpartialregressioncoefficientsfortraitsofone-yearoldfreshwatermusselHyriopsiscumingii

模型model非标准化系数 nonstandardized coefficientB标准误差 standard error标准系数standard coefficientt值t value显著性Sig.常量-157.9198.591-18.3820.000壳长x112.1951.5050.4798.1010.000壳高x25.2262.3460.1352.2280.030壳宽x322.6133.6790.2886.1470.000全高x44.9201.2960.2013.7950.000

3 讨论

3.1 相关分析与通径分析

本研究中，从各性状间的相关分析结果可知，壳长、壳高、壳宽、全高和体质量，其两两间的相关性均达到了极显著水平，这说明各变量间存在着严重的共线性问题，可以通过通径分析来解决。通径分析能够将自变量和因变量的相关关系剖分为直接作用和间接作用，同时，可以根据通径系数大小判断各自变量对因变量贡献的相对重要性，较好地解决共线性问题。近年来，通径分析已经广泛应用于水产经济动物鱼类[20-22]、虾类[23-25]、蟹类[26-27]和贝类[28-30]等的研究中。

同时，由于表型相关分析只是简单地估测了两个变量间的相关系数，在多变量情况下其不能完全反映变量间真实的相关程度。通径分析能够较好地解决这些问题，探明两个性状间的真实关系。本研究中通过通径分析显示，各形态性状对体质量的直接作用效果依次为壳长>壳宽>全高>壳高，壳宽、全高和壳高对体质量的影响主要通过壳长来实现，它们的间接作用分别为0.318、0.321和0.366，表明壳长是影响1龄三角帆蚌体质量的主要性状。这与张爱菊等[18]对三角帆蚌珠蚌成蚌的通径分析结果相一致。在对其他贝类的研究中，如砂海螂Myaarenaria[31]、企鹅珍珠贝Pteriapenguin[32]、斧文蛤Meretrixlamarchii[33]、文蛤Meretrixmeretrix[34]、南澳青蛤Cyclinasinensis[35]等，壳长也是影响体质量的主要因素。

3.2 影响体质量主要性状的确定

根据刘小林等[8,24]的研究，当复相关指数或各自变量对因变量的单独决定系数及两两共同决定系数的总和∑d(在数值上R2=∑d)大于或等于0.85(即85%)时，表明影响因变量的主要自变量已经找到。本研究中通过1龄三角帆蚌形态性状对体质量决定系数分析，所用形态性状的总决定系数R2=∑d=0.933，基本接近于1，其他影响因素对体质量的影响仅为0.067。说明所列的三角帆蚌形态性状是影响体质量的重点性状，其他无测度的性状对体质量的影响较小，基本可以忽略。

3.3 对选择育种的指导意义

在本研究中，从直接决定系数分析，壳长对体质量的决定程度最大，达到22.9%，在三角帆蚌选择育种过程中可以考虑将壳长作为育种目标性状。而王辉等[12]认为，育种决策时只考虑直接决定系数是不全面的，因为由于基因的多效性、连锁和共同环境的影响，生物性状均彼此相关，综合决定系数既包含直接决定系数又包含间接决定系数，信息量较大更具有决策意义。从分析结果看，三角帆蚌壳长、壳高、壳宽、全高均不是体质量的限制性因素，它们的综合决定效应分别为0.641、0.287、0.317和0.275。壳长对体质量的决定效应依然最大，但是综合决定系数包含的信息量更大，在实际育种应用中更有意义。

在贝类选择育种中，通常其自身的某一特定性状(如体质量等)就能够直接反映其生产性能。珍珠蚌的选择育种不同于其他贝类，其主要以提高珍珠的生产性能为目标，较难直接测得其某些特定育种目标性能。张根芳等[36]早期研究已经表明，珍珠增长与蚌总重的相关性最高。张爱菊等[18]的研究也表明，活体蚌质量对珍珠重的增加具有完全的决定作用。因此，在三角帆蚌的选择育种中，为提高珍珠产能，应该以体质量作为育种目标性状。在形态性状中，由于壳长对体质量的决定效应最大，也可作为育种目标性状。