时间透镜成像系统中泵浦脉冲的优化研究

,

(浙江工业大学 信息工程学院,浙江 杭州 310023)

时间透镜成像系统的实现方式可分类为基于电光相位调制器、基于交叉相位调制、基于和频与差频效应和基于四波混频效应[1]。而由于这四种实现方式的原理均不相同,因此影响成像系统误差的因素也不相同。例如:在基于交叉相位调制的时间透镜成像系统中,交叉相位调制和四波混频效应同时存在,此时四波混频效应是影响成像系统误差的主要因素；而在基于四波混频效应的时间透镜成像系统中,同样也存在四波混频效应和交叉相位调制,但在这种情况下,交叉相位调制就成为了成像系统误差的主要影响因素[2-3]。在时间透镜成像系统中,除了自相位调制、交叉相位调制和高阶色散会影响四波混频时间透镜成像的性能之外,泵浦脉冲也会对成像系统产生影响。四波混频时间透镜成像系统首先将一个泵浦脉冲经过色散光纤,使之获得啁啾,然后将色散光信号与带有啁啾的泵浦光发生四波混频作用,从而实现对输入信号的二次相位调制。当泵浦光和信号光发生四波混频作用时,泵浦光的相位和幅值将会转换到信号光中,此时泵浦脉冲的相位和幅值将会对成像系统产生较大的影响[4-5]。研究表明:泵浦脉冲的初始宽度越小,泵浦脉冲的调制窗口就越大,成像效果就越好。但相对地,泵浦脉冲越窄,成像就会越困难且高阶色散对成像系统的影响越明显,会大大降低成像系统的成像效果[6]。因此,探究泵浦脉冲初始宽度的优化问题有着重要的价值。笔者从四波混频时间透镜成像系统的成像原理出发,通过理论分析,得出泵浦脉冲的初始宽度与放大倍数、输入光纤的二阶色散、信号初始宽度、信号脉冲间隔及分组脉冲的脉冲个数等参数满足一定的关系,最后通过定量分析法,通过数值仿真验证了相关理论。

1 成像原理

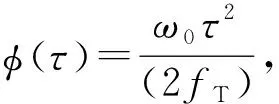
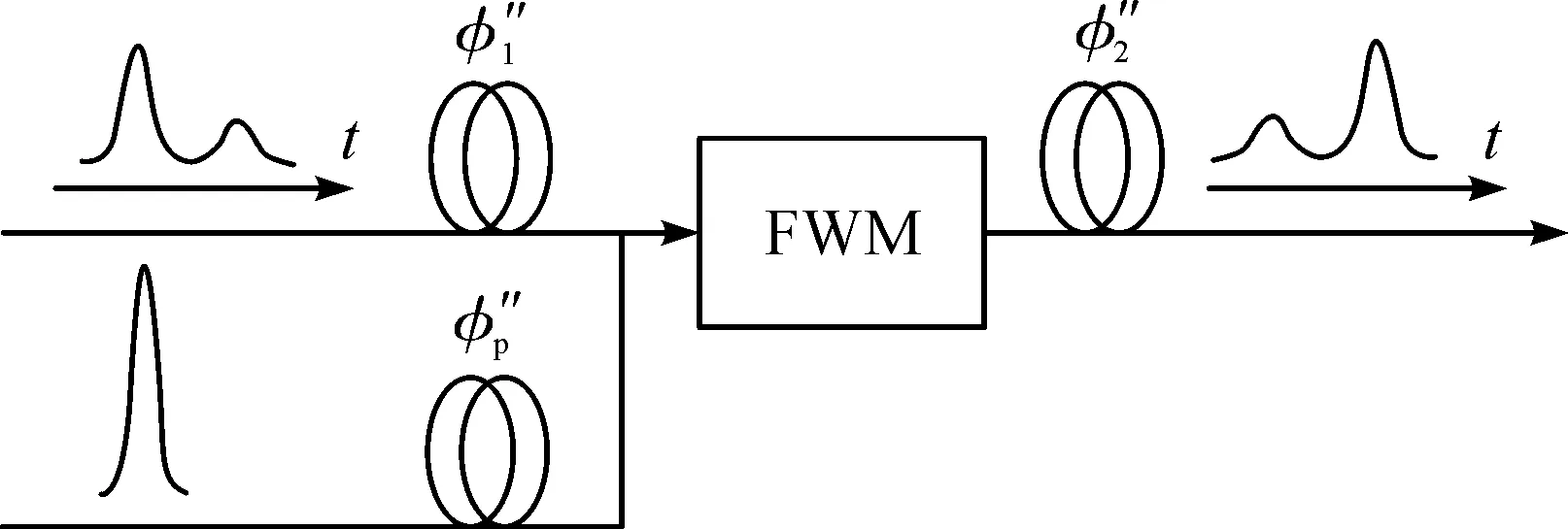
图1 四波混频时间透镜成像系统Fig.1 The structure of FWM time lens imaging system

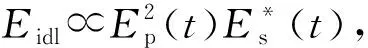
设输入时间透镜的初始信号为Ain(0,τ),输出信号为Aout(z,τ)。当光纤的二阶色散满足时间透镜成像条件[10]为

(1)

此时,输出信号为

(2)

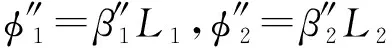
2 理论分析

四波混频时间透镜成像系统的传输条件需满足L≈LD且L≪LNL,由此可得

(3)

考虑信号是高斯脉冲的情况。设入射光场具有高斯脉冲[11]情形为

(4)

式中T0为脉冲的半宽度,即峰值强度1/e处的脉冲宽度。将式(4)进行傅里叶变换并对变换后的ω进行积分,可得沿光纤长度上任意一点z处的振幅为

(5)

此时可以看出高斯脉冲在传输过程中形状是保持不变的,但宽度T1随着z的增加而增加,此时信号宽度变为

(6)

式中:T1为信号宽度;T0为脉冲半宽度;z为传输距离。

从四波混频时间透镜成像系统的原理出发:泵浦脉冲经过色散光纤之后带有啁啾,只要啁啾泵浦脉冲的宽度大于信号脉冲的宽度,啁啾泵浦就能实现对信号的二次相位调制;同时在啁啾泵浦对信号作用的时间内,若泵浦脉冲的包络保持足够的平坦,就能实现比较完美的成像,如图2所示。那么,带有啁啾的泵浦脉冲宽度Tp(z)需远大于经过色散的信号宽度Ts(z),即

Tp(z)≫Ts(z)

(7)

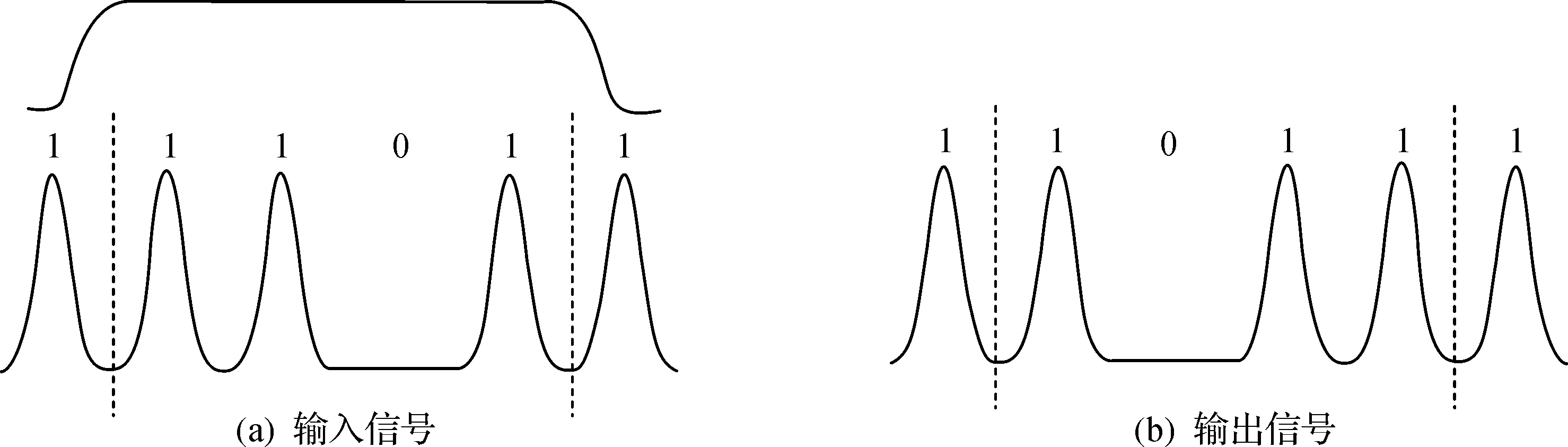
图2 带有啁啾的泵浦脉冲与信号的作用Fig.2 The effect of pump pulse with chirp and signal light

由式(6)可以求得经过输入色散光纤展宽后的信号脉冲和泵浦脉冲的脉冲宽度,并将式(3)带入式(6)可得

(8)

(9)

对于四波混频时间透镜成像系统来说,会有很多产生误差的因素,比如自相位调制和交叉相位调制等,为了提高成像系统的成像效果,需要减小这些因素的影响。1) 信号脉冲和泵浦脉冲的自相位调制会导致脉冲频谱的展宽[12]。为了解决这个问题,就需要适当减小信号光峰值功率P0和泵浦光的峰值功率Pp,同时还需要增大信号脉冲和泵浦脉冲所经过的色散光纤的长度。2) 光纤传输过程中的非线性效应会导致脉冲包络的畸变[13]。因此,为了减小非线性效应并增大色散效应,就需要适当减小信号的峰值功率P0,同时还需要减小信号初始宽度T0或者增大输入光纤的二阶色散。从上面两点可以得出,对于四波混频时间透镜成像系统来说,无论是为了减小自相位调制还是为了减小非线性效应,都需要满足条件:信号脉冲和泵浦脉冲的输入光纤长度足够长或者输入光纤的二阶色散足够大。已知一般情况下,当时间透镜实现时间放大的功能时,信号的初始脉冲宽度T0会特别小。因此,结合以上条件可得

(10)

设Δt为输入信号脉冲间隔,n为分组脉冲的脉冲个数,即n个色散脉冲信号与一个啁啾泵浦脉冲发生四波混频作用,将式(8,9)带入式(7),并利用式(10)进行化简,可得

(11)

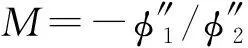
(12)

从式(12)得出:泵浦脉冲初始宽度与放大倍数、输入光纤的二阶色散、信号初始宽度、信号脉冲间隔和分组脉冲的脉冲个数均有关。更具体的关系:当信号的初始脉宽越窄,泵浦脉冲的初始脉宽也需要更窄,这符合我们的直观经验,因为信号脉冲越窄,通过色散光纤之后脉冲展宽地越大,所以相应的泵浦脉冲也要越窄;当信号输入光纤的二阶色散越大,泵浦脉冲就需要越窄,这是因为二阶色散越大,信号展宽地越严重,相应的泵浦脉冲也就需要越窄。泵浦脉冲的宽度和成像系统的放大倍数M有关,但是当M远远大于1时,此时式(12)可以化简为

(13)

从式(13)可以看出:当M远远大于1时,成像系统的放大倍数与泵浦脉冲初始宽度没有关系。

3 数值仿真

设输入信号为脉冲宽度0.2 ps,间隔1 ps的双脉冲,输入光纤的二阶色散系数为20 ps2/km,光纤长度为1 km,成像系统的放大倍数为20,通过变量分析法,验证式(12,13)。现引入绝对偏移Δτshift和相对偏移Δpshift两个变量,用来衡量影响式(12)中的各参数对成像系统引起的误差。其中,Δτshift为成像系统输出脉冲信号的宽度与理论值的差值,Δpshift=Δτshift/Tout为宽度差值与输出宽度的比值。Δτshift越大表明成像系统的绝对误差越大,Δpshift越大表明成像系统的相对误差越大。仿真结果如图3所示。

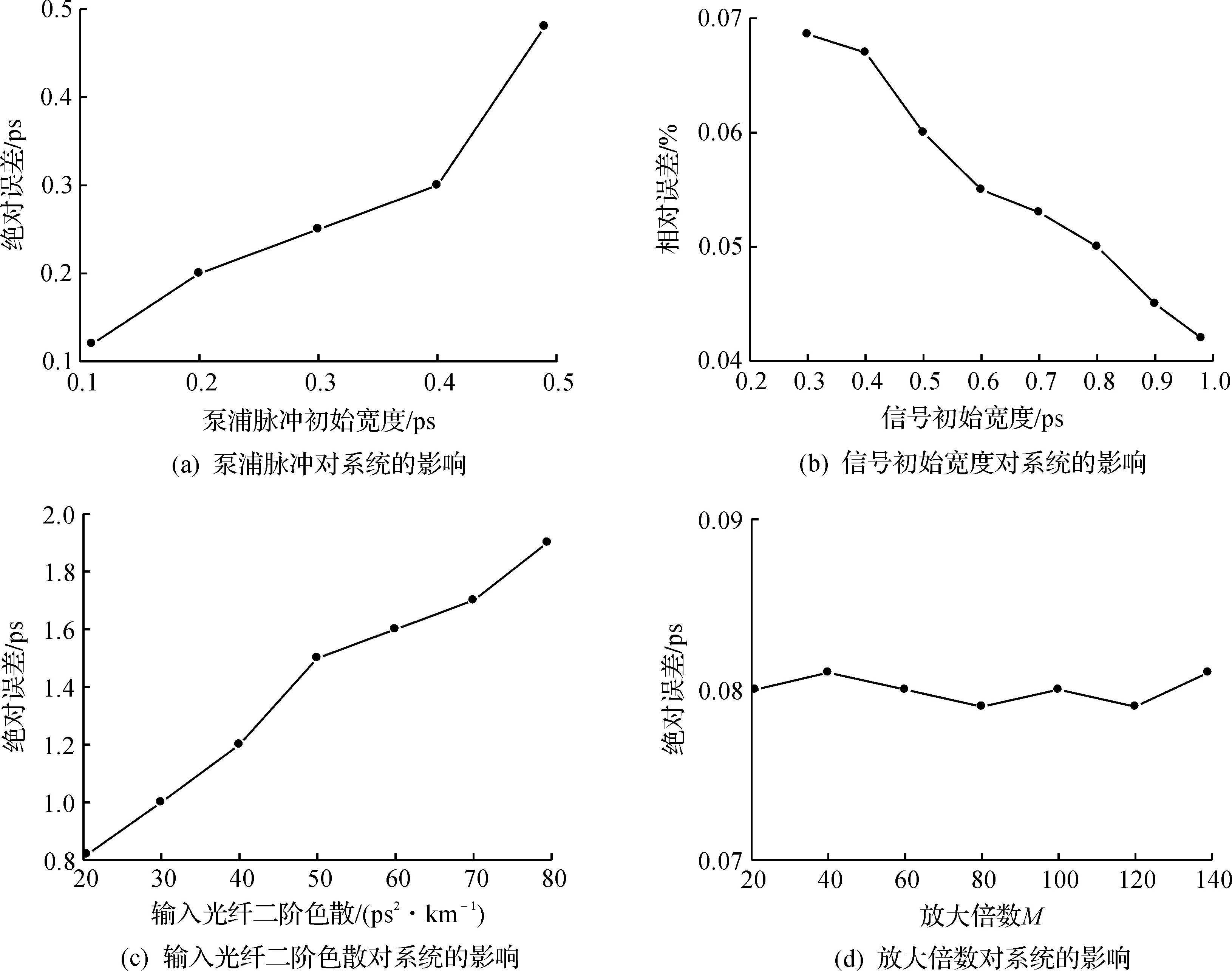
图3 不同因素对成像系统的影响Fig.3 Effect on the imaging system for different factors

图3(a)只改变泵浦脉冲的初始宽度,发现成像系统的绝对误差Δτshift随着泵浦脉冲初始宽度的减小而减小。图3(b)只改变信号初始宽度,发现成像系统的相对误差Δpshift随着信号初始宽度的增加而减小。图3(c)只改变输入光纤的二阶色散,发现系统的绝对误差Δτshift随着输入光纤二阶色散的增大而增大。图3(d)只改变放大倍数,发现当放大倍数远大于1时成像系统的绝对误差Δτshift几乎不变。因此,数值仿真结果与理论分析相吻合。

4 结 论

四波混频时间透镜成像系统的泵浦脉冲初始宽度越窄,成像系统的误差就越小。但相应地,泵浦脉冲过窄时,经过色散光纤后的脉冲畸变就越严重,反而会增大成像系统的误差。因此,需对泵浦脉冲进行优化,使成像系统的误差达到最小值。通过理论分析,得出泵浦脉冲的初始宽度与放大倍数、输入光纤的二阶色散、信号初始宽度、信号脉冲间隔及分组脉冲的脉冲个数满足一定的关系。那么就可以通过关系式,对成像系统进行误差补偿,例如,从数值仿真中发现:误差随着信号脉冲的减小而增大,此时,可以通过采用较窄的泵浦脉冲或者通过减小输入光纤的二阶色散来补偿误差,以达到较理想的成像效果。因此笔者对泵浦脉冲的优化研究为以后探究泵浦脉冲对成像系统的影响有着积极的作用。