两层弹性软基底中压电薄膜的屈曲分析

,

(浙江工业大学 机械工程学院,浙江 杭州 310014)

薄膜材料在先进技术领域有着非常广泛的应用,尤其是在微纳机电系统[1]和柔性电子器件领域[2-4]。自从Bowden等[5]的研究工作表明柔性基底上薄膜的屈曲可以被控制以来,许多学者对薄膜基底系统的屈曲问题进行了大量的理论研究[6-9],并取得了很大的进展。但是表面屈曲可能会使薄膜和基底发生脱层断裂是双层结构一个很大的弊端[10]，而3层结构能够很好的缓解这一问题,在可弯曲和拉伸的集成电路中有广泛的应用。Kim等[11]制造出的PI/Si-CMOS/PI集成电路不仅仅具有良好的导电性能,而且具有优越的可弯曲性能。杨加伟等[12]从理论上分析了夹在两个柔性层中薄膜的正弦模态屈曲问题,得到了屈曲临界薄膜应力、波数和平衡状态下的波幅解析表达式,针对不同的刚硬薄膜和柔性层的弹性模量,当刚硬薄膜相对于上下柔性层越硬,就越容易发生屈曲。然而,压电材料因其独特的力电耦合特性作为一种智能材料有着普通材料不可比拟的优势,压电薄膜弹性基底结构也有着非常重要的作用。Qi等[13]制造出一种波浪状的压电条带结构,表明这种结构可以适应更高的压缩和拉伸应变,可以应用在拉伸能量收集装置。Zhou等[14-15]从理论上分析了压电薄膜弹性基底结构在压应力作用下和预拉伸基底导致屈曲的问题,得到了屈曲的临界条件。

受到3层结构可以有效缓解双层结构屈曲时容易导致薄膜和基底脱层断裂和提高结构可弯曲性能的启发,从理论上分析了关于压电薄膜3层结构褶皱形式的屈曲问题,采用线性扰动方法分析得到了屈曲的临界应变、波数、波长和幅值的解析表达式,并且发现当3层结构退化为双层结构时,其解能退化成已有的结果。另外,对比分析了压电薄膜3层结构和弹性薄膜3层结构,发现压电薄膜比弹性薄膜有更强的抵抗屈曲变形能力。

1 压电薄膜的基本方程

基于非线性薄板理论和压电基本理论,假设压电薄膜的厚度为hf,长度为L,则压电薄膜内的电势表示[16]为

(1)

式中:φ(0)为基准电势;φ(1)为外加电势;φ(2)为诱导电势。忽略初始微弱电场,因为压电薄膜无外加电势,所以φ(0)和φ(1)为零,诱导电势与压电薄膜的弯曲变形有关。

压电薄膜内的电场强度为

(2)

压电薄膜的本构方程为

(3)

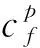
(4)

压电薄膜的几何方程为

(5)

式中:εmid,εbend分别为压电薄膜中平面应变和弯曲应变,且有ε11=εmid+εbend;u为压电薄膜x方向的位移;w为压电薄膜的挠度。

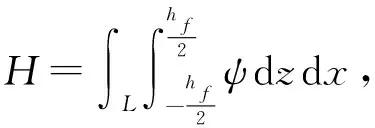
(6)

式中:N,T分别为压电薄膜内的膜力和与弹性软基底界面间的剪切力,可表示[6]为

(7)

2 3层结构模型描述

如图1所示,厚度为hf的压电薄膜夹在厚度分别为Ht和Hb的两层弹性软基底中,压电薄膜的极化方向为其厚度方向。假设弹性层的厚度相比于压电薄膜而言无限厚,上弹性层的上自由面和下弹性层的下自由面完好地固定在刚性面上。当压电薄膜受到的压应力超过屈曲临界应力时,压电薄膜可能会发生如图1所示的褶皱屈曲失稳。考虑到压电薄膜y方向的长度远远大于其屈曲的波长和幅值,所以可以简化为平面应变问题。

3 屈曲特征量分析

根据已有的研究,薄膜和基底间界面的剪切力

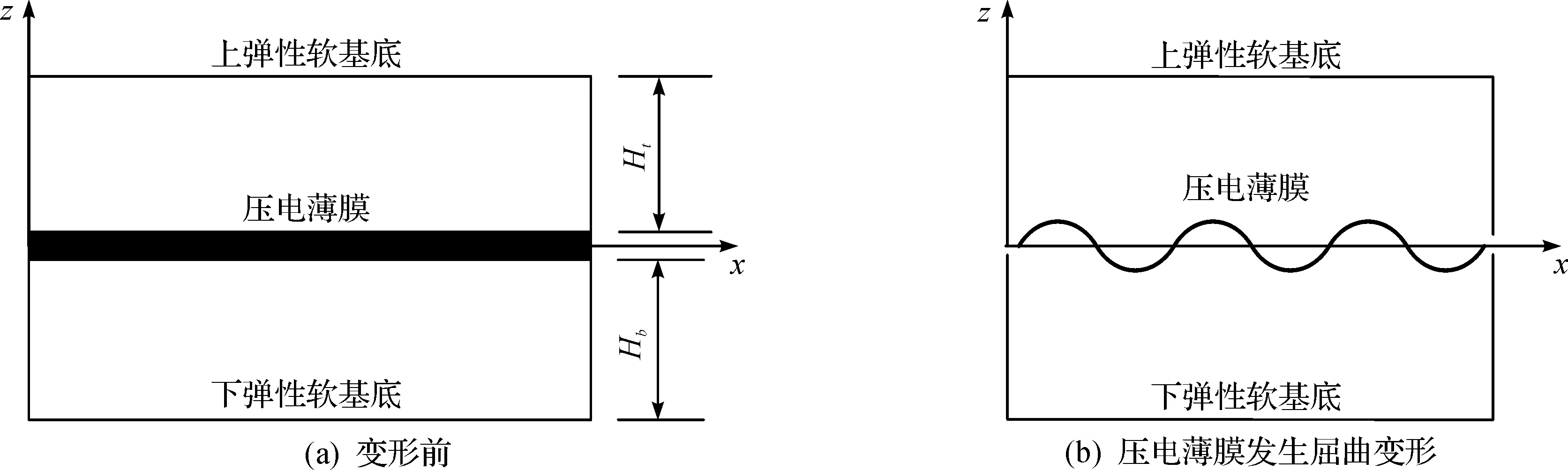
图1 模型描述Fig.1 Model description

可以忽略,且膜力分布是均匀的[6-7]。则压电薄膜的力电耦合控制方程式(6)可简化为

(8)

式中:Δp=pt-pb为上下弹性软基底施加在压电薄膜的压力差。

假设压电薄膜屈曲变形的挠度和电势分别为

(9)

式中:A,B分别为幅值;k为波数。代入式(8)的第2式,得到

(10)

式(10)代入式(8)的第1式,得到

(11)

在平面应变下,可以利用弹性力学Airy应力函数求解Δp=pt-pb。考虑到弹性软基底的上下自由表面是固定的,内边界的位移满足周期性的正弦形式,Airy应力函数可以假设[12]为

F(x,z)=f(z)cos(kx)

(12)

F(x,z)需要满足双调和方程▽2▽2F(x,z)=0,结合式(12),得到特征方程为

F(4)-2k2F(2)+k4F=0

(13)

求解方程式(13),得到

F(x,z)=[ekz(C1+C2z)+
e-kz(C3+C4z)]cos(kx)

(14)

式中Ci(i=1,2,3,4)为待定常数。利用数学关系式

(15)

式(14)可以化简为

F(x,z)=[D1cosh(kz)+D2sinh(kz)+
zD3cosh(kz)+zD4sinh(kz)]cos(kx)

(16)

式中:D1=C1+C3;D2=C1-C3;D3=C2+C4;D4=C2-C4,其值由边界条件确定。

弹性基底内的应力分量为

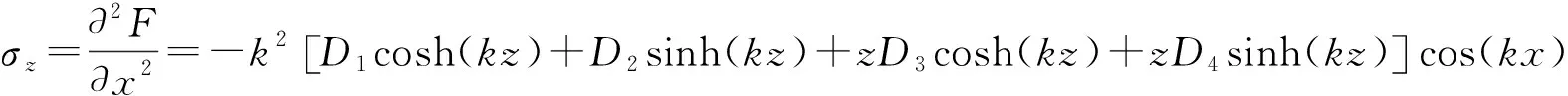
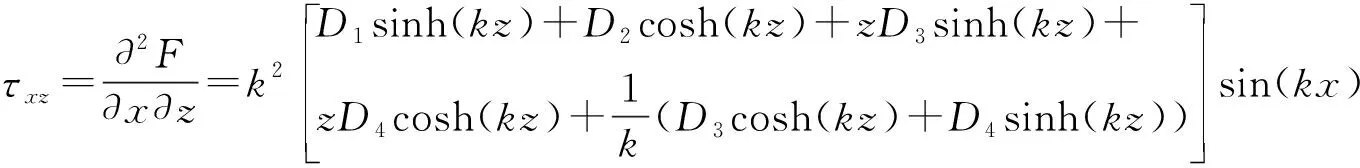
(17)

平面应变问题的弹性本构方程为

(18)

对式(18)积分可得位移分量为

(19)

式中:E,ν分别为弹性软基底的弹性模量和泊松比。注意到弹性软基底的厚度相比于压电薄膜而言是无限大的,所以这里忽略压电薄膜的厚度,则上下两层弹性软基底的边界条件可表示为

z上基底=Ht,u=w=0;z=0,w=Acos(kx),τxz=0

z下基底=Hb,u=w=0;z=0,w=Acos(kx),τxz=0

(20)

将式(20)代入式(17)中的第2式,可得

(21)

从而有

(22)

假设压电薄膜所受的初始膜力N0=σ0hf,代入到式(11),可得

(23)

将式(22)代入式(23),可得

(24)

压电薄膜屈曲的临界条件是在压电薄膜内的膜力取极小值。求解∂σ0/∂k=0得到临界波数为

(25)

(26)

将式(25)代入到式(24),可得临界压应力为

(27)

(28)

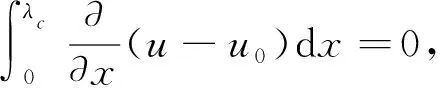
(29)

利用式(26,27),式(29)可表示为

(30)

4 数值结果与讨论

数值分析以PZT-5H压电材料为例,其相关的材料参数如表1所示,由表1中的相关数据可以计算出压电薄膜的压电耦合系数。

表1 PZT-5H相关材料参数Table 1 PZT-5H related material parameters

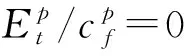
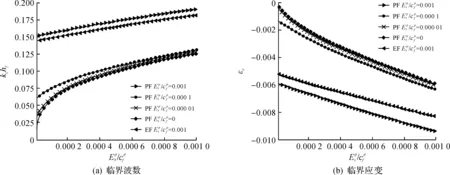
图2 屈曲特征量与材料弹性模量比的关系Fig.2 The relationship between the characteristic of buckling and the ratio of elastic modulus of material

图3描述了归一化屈曲幅值与施加给薄膜的初始压应力和屈曲临界压应力比的关系。从图3中可以看出:在初始压应力和临界压应力之比小于1时,幅值不存在,这时薄膜没有发生屈曲变形,之后幅值随着压应力之比的增加而增加,另外还可以看出压电薄膜结构的幅值比弹性薄膜结构的幅值大。

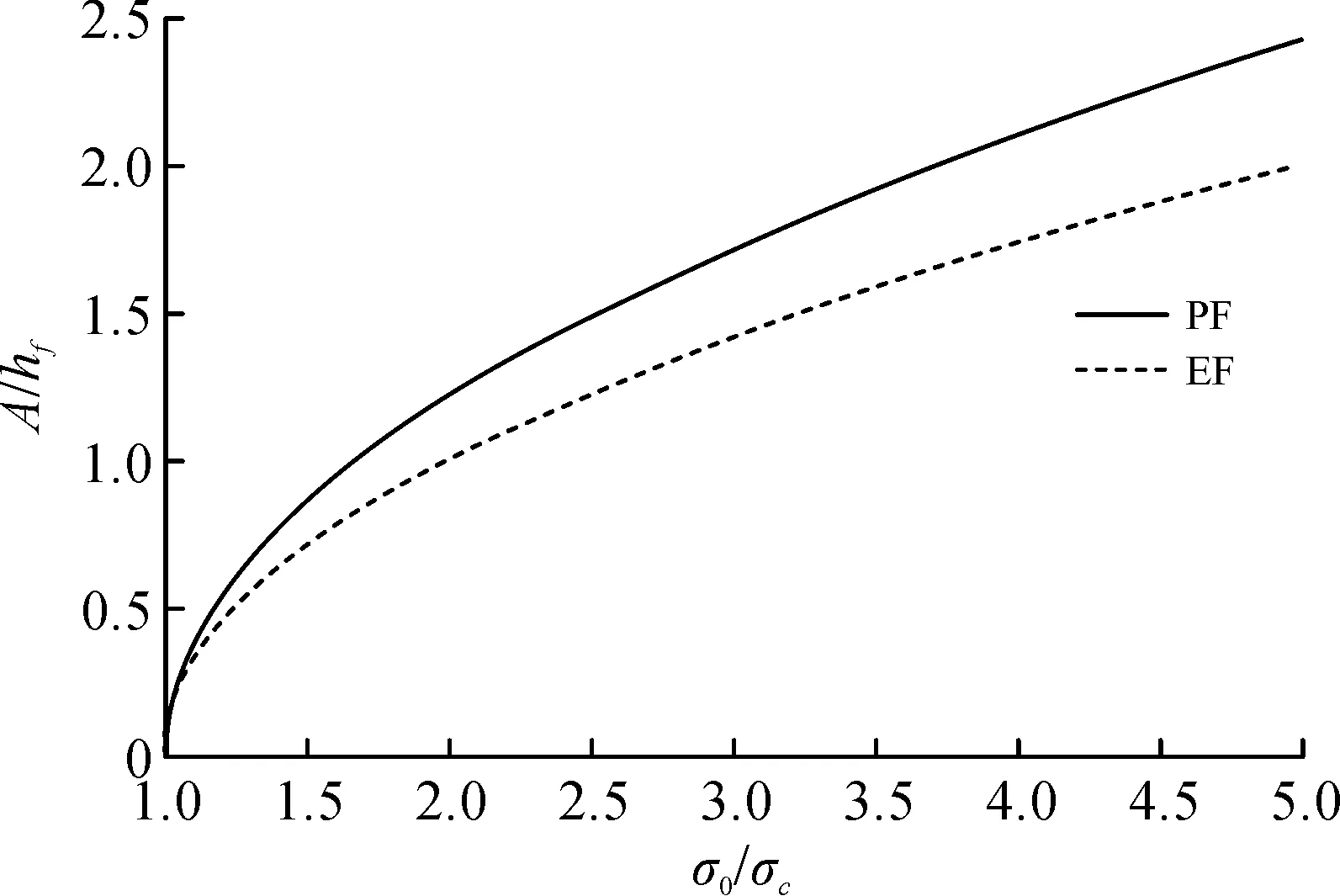
图3 屈曲幅值与应力比的关系Fig.3 The relationship between the buckling amplitude and the stress ratio

5 结 论

研究了夹在两层弹性软基底中压电薄膜的屈曲问题,从理论上分析得到了压电薄膜屈曲的临界应变、波数、波长和幅值的解析表达式,推导出的解析表达式进一步退化成双层结构形式时,获得的解与已有文献的结果完全一致;数值分析了屈曲临界应变和临界波数随着材料参数的变化关系和屈曲幅值随着初始压应力变化的关系。结果表明:压电薄膜相比于弹性软基底越刚硬时,屈曲平衡状态下波数越小,波长越大,屈曲临界应变越小,压电薄膜更容易发生屈曲变形。通过对比压电薄膜3层结构与弹性薄膜3层结构,发现压电薄膜相比弹性薄膜,抵抗屈曲变形的能力更强。