液压成形波纹管减薄率的数值模拟研究

,,,,,,

(1.平高集团有限公司,河南 平顶山 467001;2.浙江工业大学 机械工程学院,浙江 杭州 310014)

液压成形是波纹管最常用的成形方法之一,具有管坯受压均匀和减薄量适中等特点[1-2]。影响波纹管液压成形质量的因素有很多,如轴向进给、成形内压、材料性能和模具尺寸等,且诸多因素并非独立存在而是相互联系的。如果各影响因素之间匹配不合理,将会产生皱褶、屈曲和破裂等缺陷[3-4]。皱褶(wrinkling)主要是因为成形内压不足和轴向进给过大引起的,皱褶的数量和位置与轴向进给、成形内压、管坯尺寸等因素有关。皱褶可分为有益皱褶和有害皱褶两种形式[5]。屈曲(buckling)是一种失稳现象,是因为成形压力不足、轴向进给过大引起的,与皱褶不同,一旦发生屈曲,胀形过程将不能继续进行下去,因为屈曲后管坯的变形无法再控制[6]。破裂(bursting)是因为成形压力过高、轴向进给不足导致壁厚迅速减薄、管坯厚度不能承受成形压力引起的[7]。

成形内压和轴向进给是波纹管液压成形最主要的两个工艺参数,合理的参数设计可以预防各种缺陷的产生[8]。陈杰等[9]采用DYNAFORM软件模拟了X形管件的液压成形过程,得出以下结论:梯度内压加载路径的成形质量要显著好于线性内压加载路径;成形内压和轴向进给是否匹配对X形管液压成形质量有很大的影响;随着模具圆角半径的增大,成形后X形管件壁厚分布均匀性增加。Yang等[10]基于响应面和灵敏度分析法,以成形零件与模具贴合程度为约束条件,以最小壁厚变化率为优化目标,通过多次模拟确定了最优加载路径。KOC等[11]利用塑性理论和薄膜理论建立了管件液压成形失效的解析模型,预测了内压、轴压和壁厚减薄率等工艺参数。夏巨谌等[12]对多通管挤压成形过程的力学行为进行了研究,采用应变样条法获得了挤压力、胀形力和平衡力之间的数学关系式。Fann等[13]运用有限元软件LS-DYNA对T形管件胀形过程进行了数值模拟,比较了不同轴向位移与胀形内压的匹配关系,优化了轴压胀形加载路径。

上述研究表明:成形内压和轴向进给以及两者的匹配关系对管件液压成形质量有很大的影响,波纹管除了不允许产生皱褶、屈曲和破裂等缺陷外,还应具备较高的成形质量。波纹管的厚度减薄率是衡量液压成形质量好坏的一个重要指标,过大的减薄率会严重影响波纹管的耐腐蚀性能和疲劳寿命。因此,笔者将从轴向进给和成形压力两个方面,研究液压成形参数对波纹管减薄率的影响。

1 波纹管液压成形过程中应力应变关系

液压成形过程中,波纹管的应变与应力状态有关,而厚度变化取决于应变变化。假设管坯为理想刚塑性材料,根据Levy-Mises塑性流动理论,成形过程中管坯材料的应力与应变之间存在下列关系[14],即

(1)

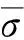
因波纹管的管坯壁厚一般远小于其半径,属于薄壁管件,因此根据薄膜理论可以忽略径向应力σt的影响,则式(1)可简化为

(2)

由式(2)可知:当σz+σθ>0时,dεt<0,波纹管的壁厚将减薄,容易引起破裂失效;当σz+σθ<0时,dεt>0,则波纹管壁厚将增加,容易引起皱褶失效;当σz+σθ=0时,dεt=0,此时波纹管的壁厚将保持不变,这是一种理想的状态。波纹管在液压成形过程中,应尽可能做到σz+σθ=0应力状态,则壁厚减薄率最小。

2 波纹管数值模型的建立

以常见的U形波纹管为例,其几何形状如图1所示。

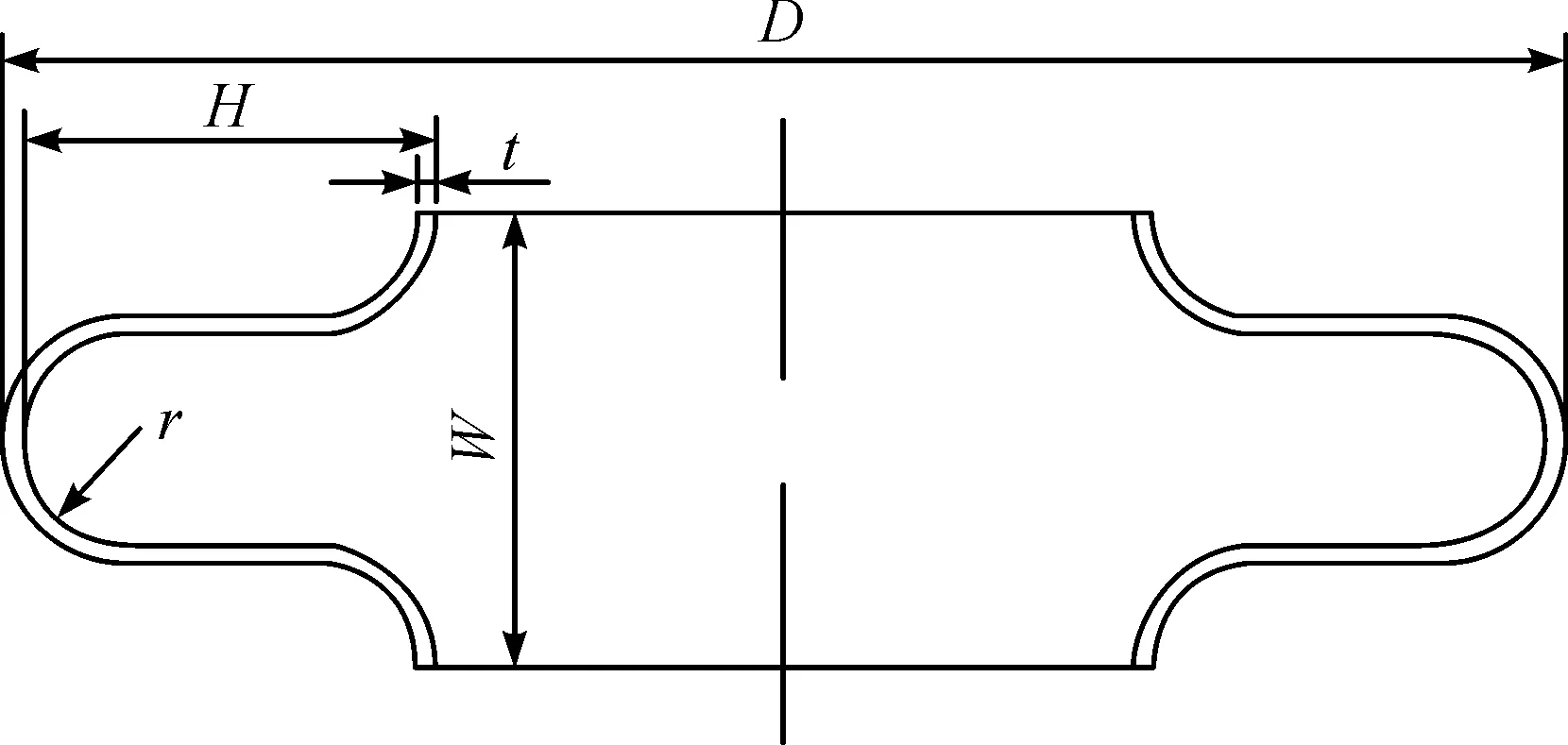
图1 U形波纹管的几何形状Fig.1 Geometry of U-shaped bellows

选取管坯的尺寸为φ114 mm×0.5 mm,轴向长度70.9 mm,模具的圆角半径均5.8 mm,直边段长度6 mm,数据见表1。

表1 U形波纹管的结构尺寸Table 1 Dimension of U-shaped bellows

波纹管液压成形数值模型由管坯、左冲头和右冲头三部分组成。由于几何形状以及载荷条件对称,故选取1/4几何实体建立模型。数值模拟采用液压成形的DYNAFORM有限元软件进行,波纹管模型网格划分情况如图2所示。相对薄壁波纹管来说,模具刚性很大,所以成形过程中左、右冲头的变形不予考虑。

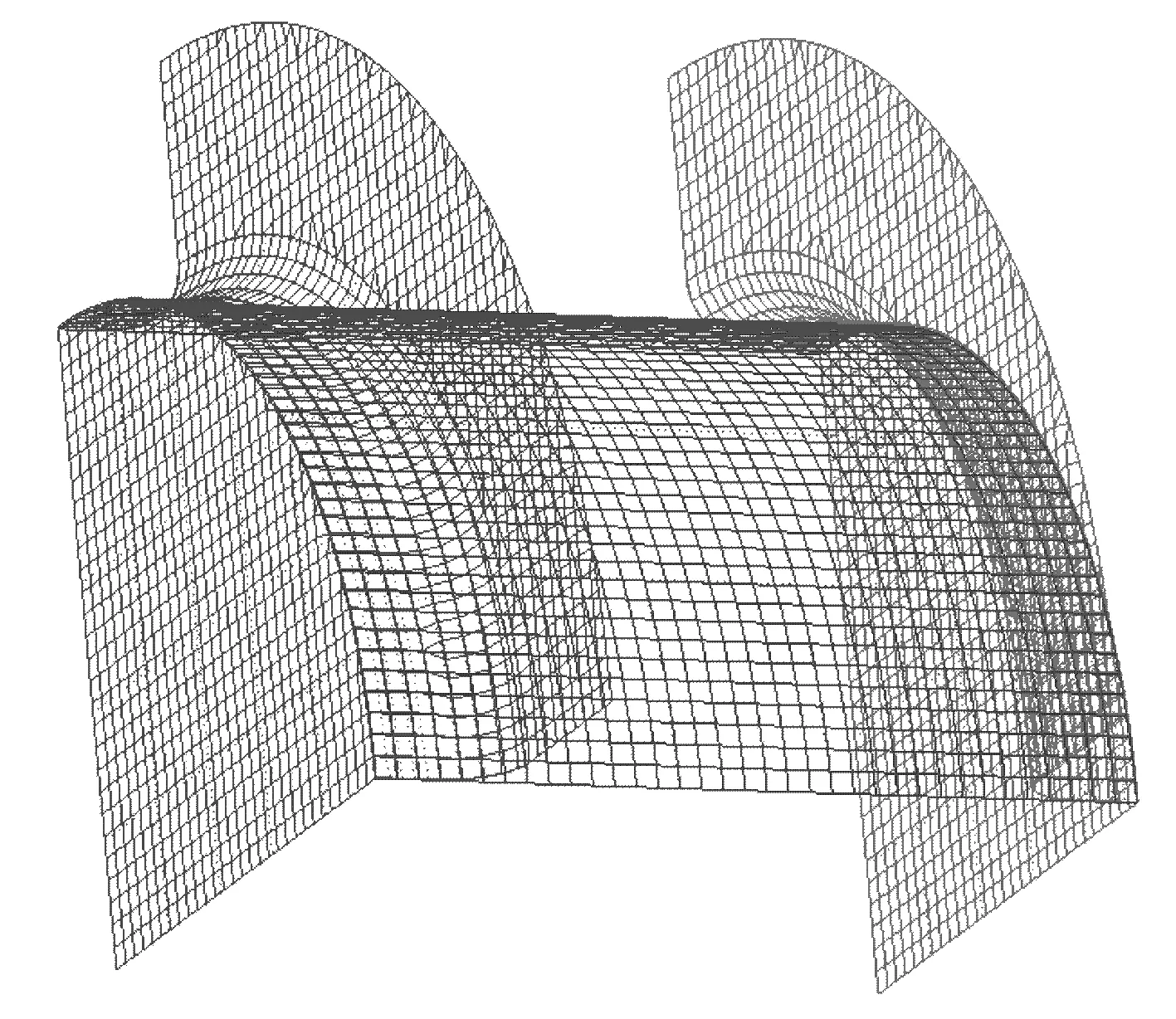
图2 波纹管液压成形有限元网格Fig.2 The finite element model of hydro forming bellows

3 加载路径对波纹管减薄率的影响

波纹管液压成形过程中的工艺参数主要包括轴向进给位移S与成形内压p,以及两者之间的匹配关系。不同的工艺参数组合得到液压成形过程各种加载路径,不同的加载路径导致管坯的不同应力分布状态,因此选择合理加载路径目的是为了使波纹管在液压成形过程中的应力分布状态尽量接近于σz+σθ=0,从而避免产生皱褶、屈曲和破裂等缺陷。

下面将对不同的加载路径下波纹管液压成形过程进行数值模拟,分析进给位移s和成形内压p等参数对波纹管减薄率的影响。

3.1 轴向进给对波纹管减薄率的影响

为研究轴向进给位移对波纹管减薄率的影响,先选定一种成形压力的加载曲线。参照工程经验参数,选取成形内压p随时间t的加载曲线,如图3所示,即初始的1 s时间内为增压阶段,压力从0线性增加至2.4 MPa,然后为保压阶段。

轴向进给位移S采用四种不同加载路径方式,如图4所示。路径1为台阶形位移加载曲线,路径2为双线性位移加载曲线,路径3为单线性位移加载曲线,路径4为二次函数位移加载曲线。四种加载路径最终的轴向进给量相等,均为17.3 mm。

通过数值模拟计算,得到上述四种加载路径下成形波纹管的厚度分布云图,如图5所示。为了更加直观地分析壁厚的分布情况,以波纹管的径向距离为横坐标,得到壁厚随径向距离的变化曲线如图6所示。

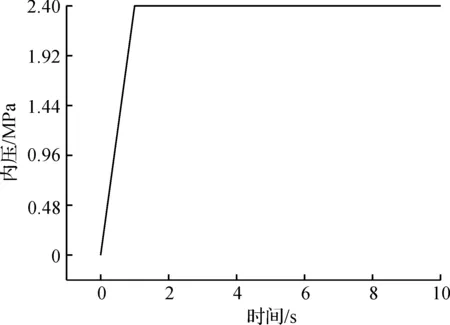
图3 不同轴向进给位移对应的成形内压加载曲线Fig.3 The loading paths of deforming pressure

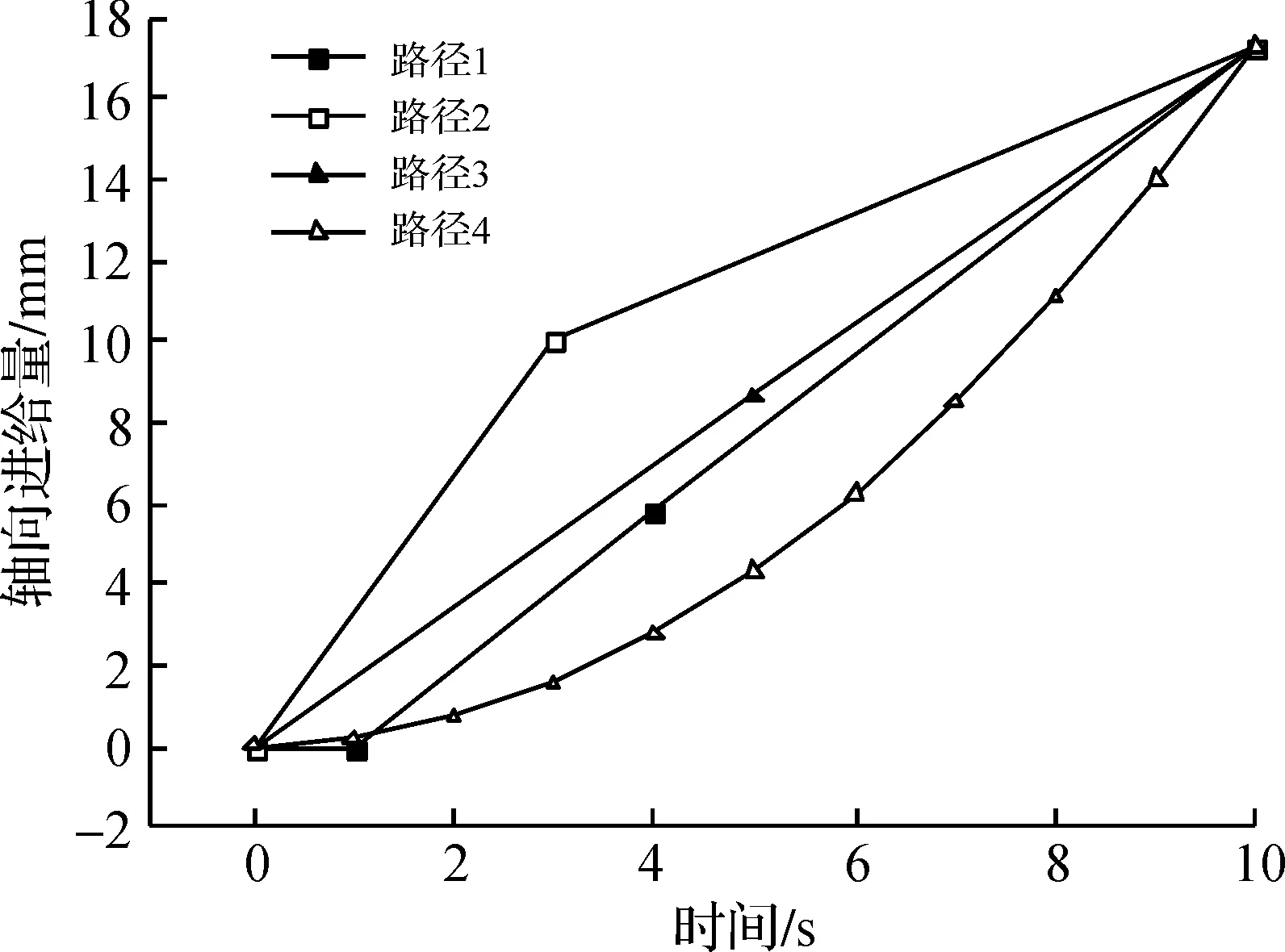
图4 四种轴向进给加载路径Fig.4 Four kinds of loading paths of axial feed displacement

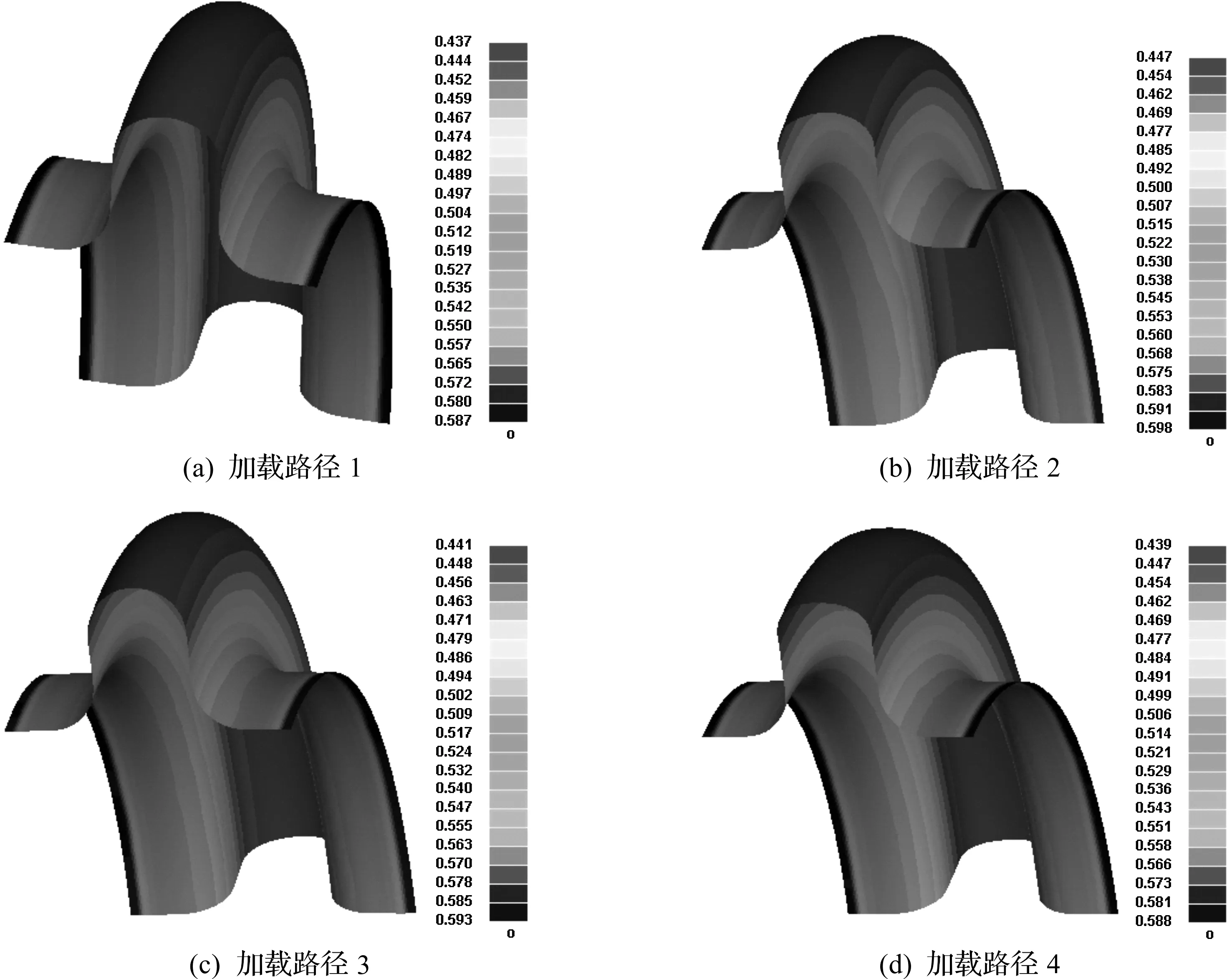
图5 四种加载路径下成形波纹管的厚度分布云图Fig.5 The bellows thickness distribution of four kinds of axial feed displacements

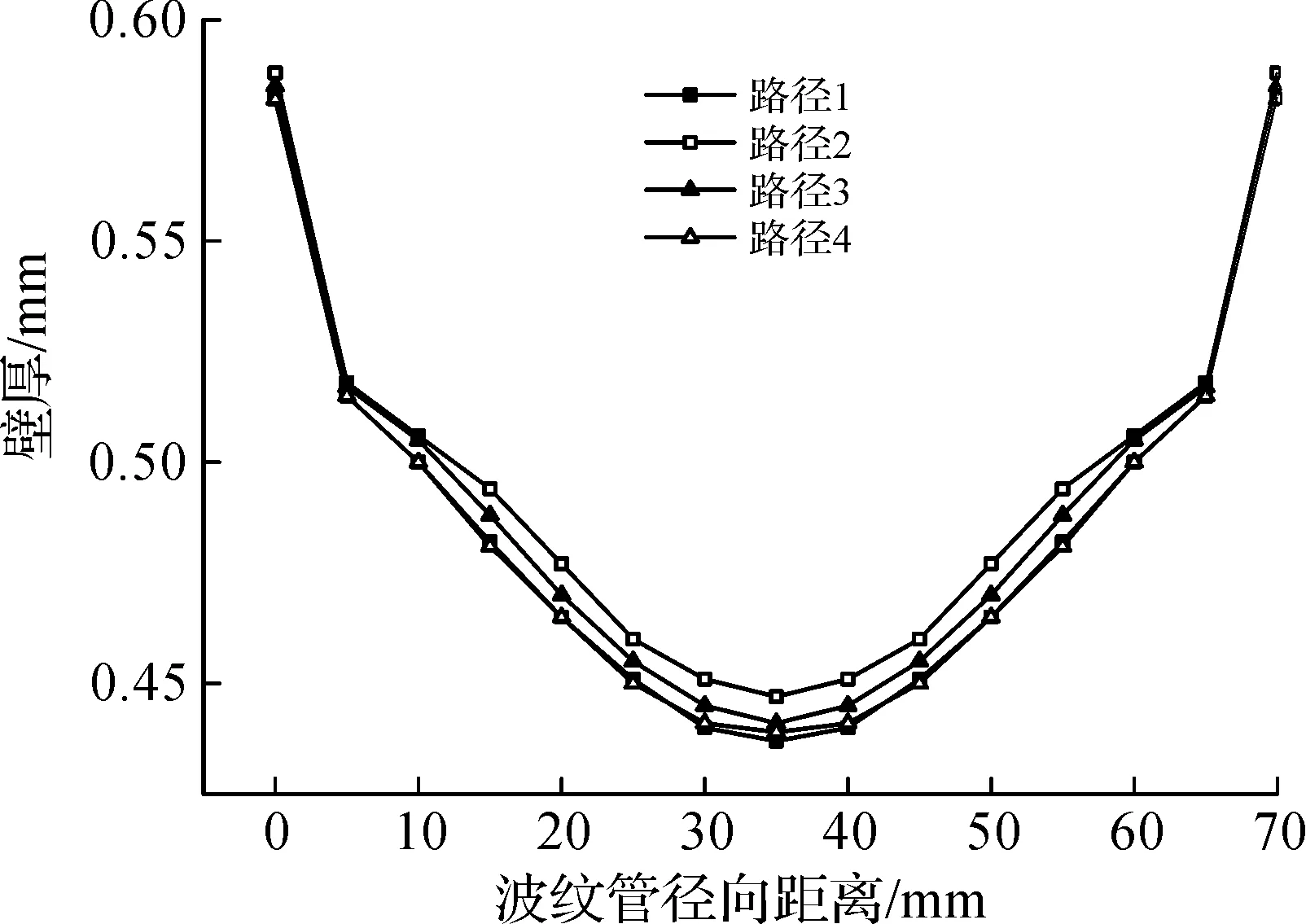
图6 壁厚随波纹管径向距离的变化曲线Fig.6 The bellows thickness varies with meridional distance(4 axial feed displacements)

由图5可见:四种轴向进给位移加载路径波纹管的厚度分布基本一致,即波谷处厚度减薄最小,从波谷到波峰厚度减薄率逐渐增大,在波峰处壁厚减薄最严重。比较四种加载路径:路径1和4的减薄率最大,路径3的减薄率次之,路径2的减薄率最小。说明在保持总轴向进给位移不变条件下,成形初期快速进给(路径2)有利于减小波纹管的减薄率。从成形过程的应力状态来看,成形初期快速进给导致轴向压应力(σz)增大,从而导致σz+σθ的减小,dεt趋向正值,厚度减薄率减小。

3.2 成形内压对波纹管减薄率的影响

选取上述轴向进给位移加载路径1,即初始的1 s时间内轴向进给为0,随后9 s时间轴向进给从0线性增加至17.3 mm,加载曲线如图7所示。

成形内压采用的四种不同加载曲线,如图8所示。不同加载路径对应的成形压力分别为2.2,2.4,2.6,2.8 MPa。

图7 不同成形内压下轴向进给的加载路径Fig.7 The loading paths of axial feed displacement

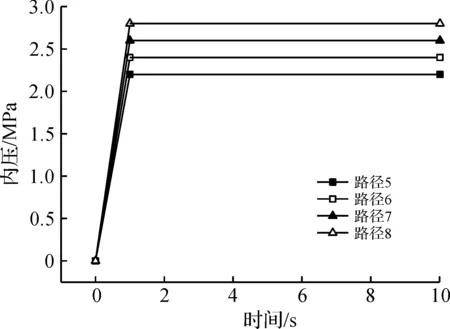
图8 成形内压的四种加载路径Fig.8 The four kinds of loading paths of deforming pressure

四种成形内压加载路径下波纹管的厚度分布规律也基本一致,即波谷处厚度减薄最小,在波峰处壁厚减薄率最大。在不同加载路径下,成形波纹管的厚度分布云图如图9所示。图中可见路径5对应的波纹管波峰处出现了明显皱褶,其余路径下均无明显缺陷。波纹管壁厚随经向距离的变化曲线如图10所示。

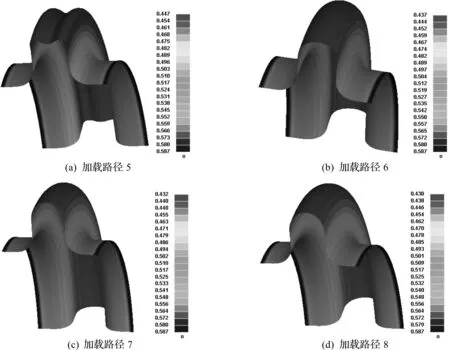
图9 四种成形内压加载路径下波纹管的厚度分布云图Fig.9 The bellows thickness distribution of four kinds of deforming pressures

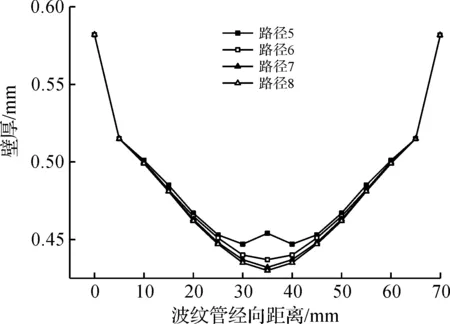
图10 四种成形内压加载路径下波纹管壁厚变化曲线Fig.10 The bellows thickness varies with meridional distance(4 deforming pressures)

比较四种成形内压加载路径,发现波纹管厚度减薄率随着成形压力的升高而增大。在加载路径5成形压力较低情况下,因成形压力与轴向进给之间匹配不合理,将导致波峰处出现明显皱褶的现象。

4 结 论

上述液压成形过程数值模拟分析表明,成形内压和轴向进给以及两者的匹配关系对波纹管的减薄率有很大的影响。通过四种轴向进给和成形内压的加载路径比较,得到下列主要结论:1) 波纹管液压成形过程中壁厚的分布规律为波谷处厚度减薄最小,从波谷到波峰厚度减薄率逐渐增大,在波峰处壁厚减薄最严重;2) 比较了四种轴向进给位移的加载路径对波纹管减薄率的影响,结果表明台阶形和二次曲线路径减薄率较大,单线性路径减薄率次之,双线性路径的减薄率最小;3) 在总轴向进给位移保持不变条件下,成形初期快速进给有利于减小波纹管的减薄率;4) 比较四种成形内压加载路径,发现波纹管厚度减薄率随着成形压力的升高而增大,如果成形压力过低,会因成形压力与轴向进给位移之间匹配不合理,导致波峰处出现皱褶的现象。