螺栓位置与换能器有效机电耦合系数的关系

杨佳婷，李娜，武婷婷，贺西平



螺栓位置与换能器有效机电耦合系数的关系

杨佳婷，李娜，武婷婷，贺西平

(陕西师范大学物理学与信息技术学院，陕西西安 710119)

研究了螺栓在换能器中部或后部(后置)位置时，对有效机电耦合系数的影响。将螺栓等效为T型四端网络，利用换能器的机电等效电路，全面分析了其对应的有效机电耦合系数与螺栓长度之间的变化关系。结果表明，螺栓处于中部时，换能器的机电耦合系数与螺栓长度呈正相关趋势；螺栓位于后端时，换能器的机电耦合系数与螺栓长度先呈正相关变化，随后呈负相关变化；相比于螺栓位于中部，后置螺栓长度的变化对有效机电耦合系数的波动比较大，但有机电耦合效率的系数数值均比中部位置螺栓的值小。这说明螺栓置于中部时机电耦合性能更好。

换能器；螺栓；有效机电耦合系数

0 引言

超声换能器是组成超声振动系统的核心部件之一。其中有效机电耦合系数是评价超声换能器声学特性的一个重要指标，有众多文献对此性能参数的影响因素进行了研究[1-5]。霍树青等[6]分析了不同的截面位置对换能器前后振速比和有效机电耦合系数的影响，并指出位移截面位于后盖板或中间时较佳。林书玉等[7]通过对径向振动电压换能器共振、反共振频率方程的推导求解，得出了有效机电耦合系数与换能器件在不同形状几何尺寸之间的相关性和依赖关系，与数值计算结果吻合。Aronov B[8]、ARNOLD F J等[9]提出了通过改变电极形状来优化换能器有效机电耦合系数的一种简单实用的方法。Siddiqui N A等[10]基于压电效应的基本原理，分别从理论和实验探究了换能器的谐振频率、反谐振频率及有效机电耦合系数与电负载阻抗(包括电阻、电感和电容)之间的变化关系。ZHANG Q等[11]推导了纵向振动压电换能器的机电耦合模型，结合能量法和机电等效电路法，得到了有效机电耦合系数与PZT陶瓷位置的关系规律。制作了原型换能器，对其进行了阻抗特性测试，实验结果与解析值吻合较好。李军等[12]探究了螺栓置于中部时的机电等效电路，给出了换能器的性能参数随螺栓长度、直径的变化曲线。实际应用中，换能器的预紧力螺栓可以设计在中部，也可以后置，之前从未有文献报道过螺栓位置对换能器的有效机电耦合系数的影响。本文对这两种情形进行了综合计算和分析比较。

本文用数值计算的方法，以材料45#钢为例，从理论上探究了压电换能器位移截面处于压电陶瓷中间位置时(这时的有效机电耦合系数最大[13])，螺栓处于中部或后置时对压电换能器机电耦合系数的影响，得到了换能器的螺栓置于中部比后置时的有效机电耦合系数高的结论。

1 压电换能器的频率方程

1.1 中部螺栓压电换能器的频率方程

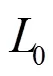
图1 中部螺栓压电换能器的结构示意图

图2 中部螺栓压电换能器的机电等效电路

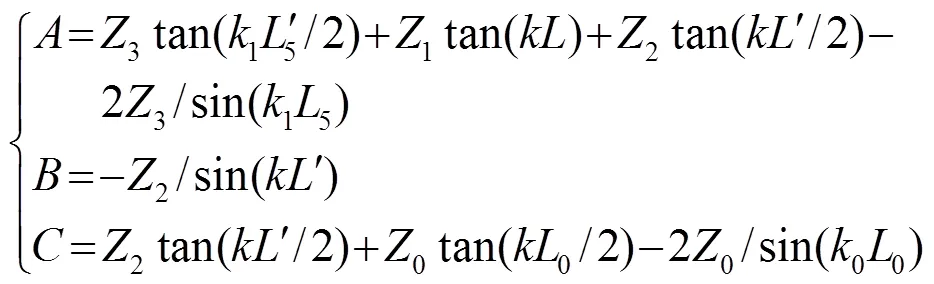
由图2可得整个换能器的输入电导纳如式(3)所示：

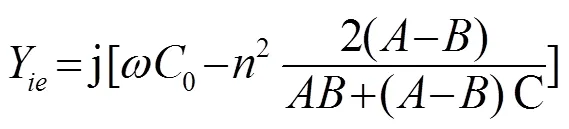
由式(1)可得换能器的共振、反共振频率方程分别如式(4)、(5)所示：

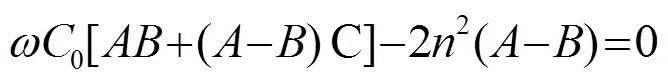
1.2 后置螺栓压电换能器的频率方程

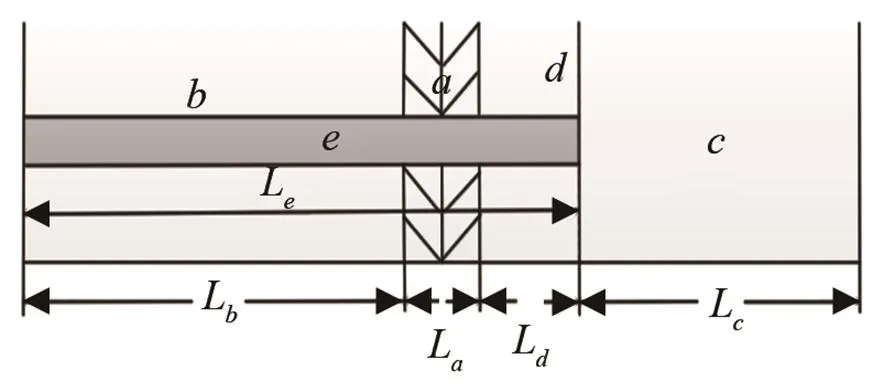
图3 后置螺栓压电换能器的结构示意图

图4 后置螺栓压电换能器的机电等效电路

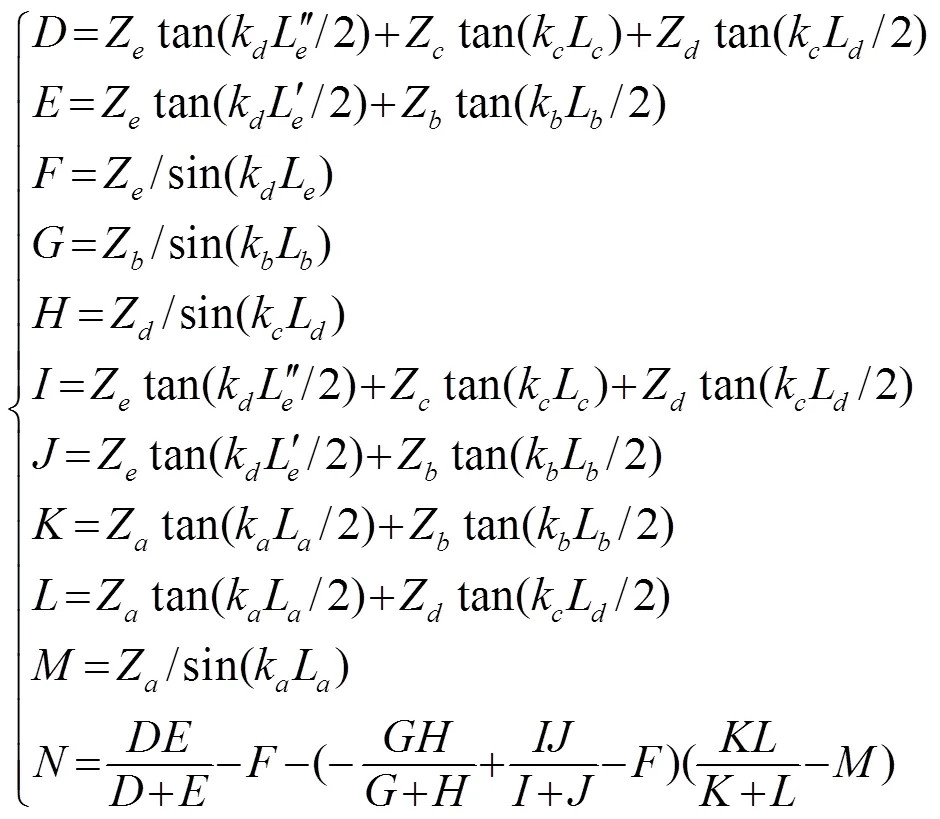
由图4可得螺栓后置时整个换能器的输入电导纳如式(8)所示：

2 螺栓位置对换能器性能参数的影响

2.1 中部螺栓与换能器共振、反共振频率及有效机电耦合系数的关系

设定换能器的总长度固定不变且为112 mm，采用45#钢作为前、后盖板材料，盖板长度为50 mm；将PZT-4作为压电陶瓷片材料，压电陶瓷片的厚度为6 mm，内径为10 mm，外径为20 mm；螺栓直径为12 mm，材料也选取45#钢。

图5、图6分别是中部螺栓换能器的共振、反共振频率、机电耦合效率与螺栓长度的关系。由图5分析可得，压电换能器的共振、反共振频率与螺栓长度呈负相关变化，且共振变化的振幅比较小，反共振趋于稳定状态。由图6分析可得螺栓的长度从20 mm变化到最长110 mm的过程中，有效机电耦合系数从0.427 9缓慢增大到0.453 4。

图5 中部螺栓换能器的共振、反共振频率与螺栓长度的关系曲线

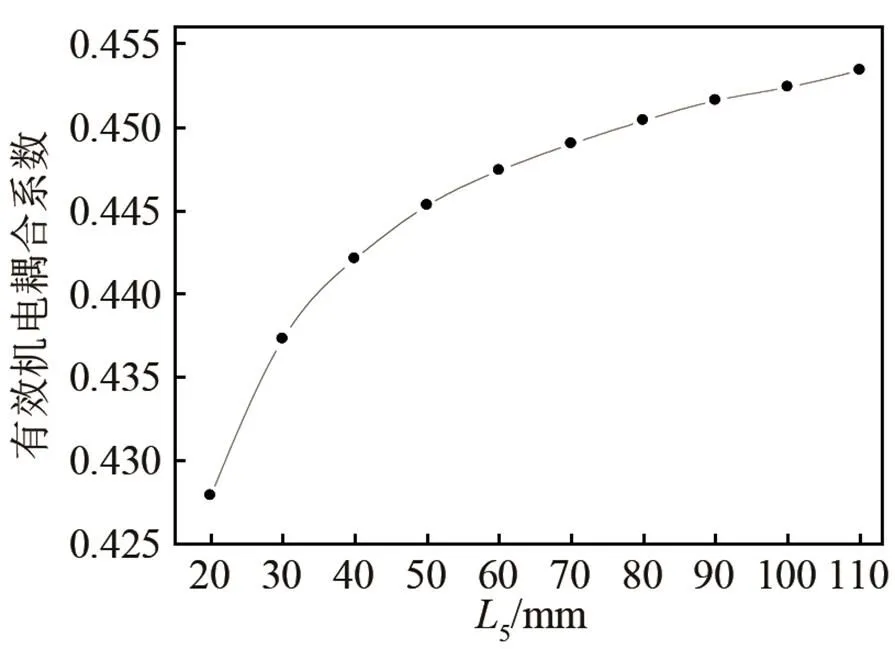
图6 中部螺栓换能器的有效机电耦合系数与螺栓长度的关系曲线

2.2 后置螺栓与换能器共振、反共振频率及有效机电耦合系数的关系

利用数值计算插值取点得到了如图7、8所示的曲线，图中曲线分别为当压电换能器的螺栓后置时，换能器的共振、反共振频率、机电耦合效率与螺栓长度之间的关系。由图7分析可得，压电换能器的共振、反共振频率随着螺栓的长度的增加而增加。共振频率随着螺栓长度的变化而缓慢变化，反共振频率随着螺栓长度的增加先缓慢增加，当螺栓长度为97.5 mm时，反共振频率发生突变，快速增加。由图8分析可得，机电有效耦合效率随着螺栓长度先缓慢增减，当螺栓长度为97.5 mm时，机电有效耦合效率快速衰减。总体分析得出，螺栓长度由65 mm增加到97.5 mm时，机电有效耦合效率由0.363 5缓慢增大到0.391 0，随着螺栓长度的继续增加，当增加到110 mm时，机电有效耦合效率快速衰减到0.180 6。

图7 后置螺栓换能器的共振、反共振频率与螺栓长度的关系曲线

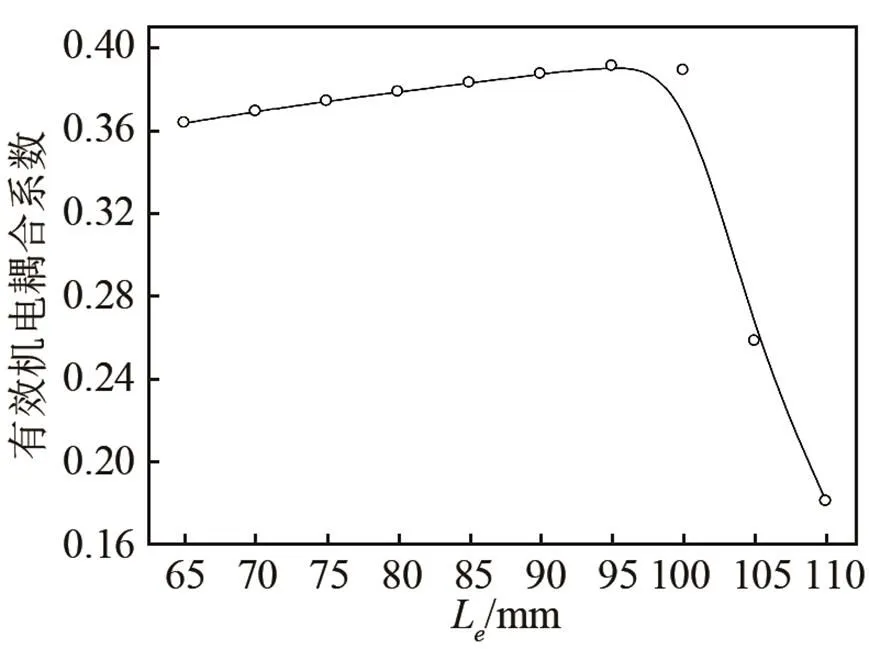
图8 后置螺栓换能器的有效机电耦合系数与螺栓长度的关系曲线

2.3 中部和后置螺栓的比较

由图6、8分析可得，当换能器的长度一定时，位于中部的螺栓换能器的有效机电耦合系数大于位于后端的螺栓换能器的有效机电耦合系数。此数据可以为后期换能器位置的选择提供参考和指导。

3 结论

通过数据分析了换能器的螺栓在不同位置时压电陶瓷的有效机电耦合系数随螺栓长度的变化规律。对螺栓位于中间位置和后端位置两种情况下，换能器的有效机电耦合系数进行分析比较，得出以下结论：

(1) 当螺栓位于换能器中部，且换能器总长保持不变时，换能器的有效机电耦合系数与螺栓的长度呈正相关变化；当螺栓位于换能器后端时，有效机电耦合系数先呈正相关变化随后快速衰减。

(2) 当位移截面位于换能器压电陶瓷元件中间位置不变时，螺栓处于中部时的有效机电耦合系数均高于螺栓后置时的有效机电耦合系数。

根据以上结论，设计换能器时，可以将其螺栓设计在换能器的中部位置来提高其机电转换效率。

[1] YARALIOGLU G G, ERGUN A S, BAYRAM B, et al. Calculation and measurement of electromechanical coupling coefficient of capacitive micromachined ultrasonic transducers[J]. IEEE Transactions on Ultrasonics Ferroelectrics & Frequency Control, 2003, 50(4): 449-456.

[2] TRINDADE M A, BENJEDDOU A. Effective electromechanical coupling coefficients of piezoelectric adaptive structures: critical evaluation and optimization[J]. Mechanics of Advanced Materials & Structures, 2009, 16(3): 210-223.

[3] KIM M, KIM J, CAO W. Electromechanical coupling coefficient of an ultrasonic array element[J]. Journal of Applied Physics, 2006, 99(7):410-416.

[4] WALLMERSPERGER T, LEO D J, KOTHERA C S. Transport modeling in ionomeric polymer transducers and its relationship to electromechanical coupling[J]. Journal of Applied Physics, 2007, 101(2):915-921.

[5] TRINDADE M, BENJEDDOU A. Effective electromechanical coupling coefficients of piezoelectric adaptive structures: critical evaluation and optimization[J]. Mechanics of Advanced Materials and Structures, 2009, 16(3): 210-223.

[6] 霍树青, 高长水. 夹心式换能器设计中截面位置的选择与分析[J]. 电加工与模具, 2009(2): 47-49.

HUO Shuqing, GAO Changshui. The analysis about the choice of the nodal surface's position in the course of the sandwich piezoelectric ultrasonic transducer's design[J]. Electromachining and Mould, 2009(2): 47-49.

[7] 林书玉. 一种新型级联式高强度功率超声压电陶瓷换能器[J]. 陕西师范大学学报(自然科学版), 2017, 45(6): 22-28.

LIN Shuyu. A new type of cascaded high intensity piezoelectric ultrasonic transducers[J]. Shaanxi Division Journal of Fan University(Natural Science Edition), 2017, 45(6): 22-28.

[8] ARONOV B. On the optimization of the effective electromechanical coupling coefficients of a piezoelectric body[J]. J. Acoust. Soc. Am., 2003, 114(2): 792-800.

[9] ARNOLD F J, MÜHLEN S S. The influence of the thickness of non-piezoelectric pieces on pre-stressed piezotransducers[J].Ultrasonics, 2003, 41(3): 191-196.

[10] SIDDIQUI N A, KIM D J, OVERFELT R A, et al. Electromechanical coupling effects in tapered piezoelectric bimorphs for vibration energy harvesting[J]. Microsystem Technologies-Micro-and Nanosystems Information Storage and Processing Systems, 2017, 23(5): 1537-1551.

[11] ZHANG Q, SHI S J, CHEN W S. An electromechanical coupling model of a longitudinal vibration type piezoelectric ultrasonic transducer[J]. Ceramics International, 2015, 41(1): 638-644.

[12] 李军, 贺西平, 丁少虎. 预应力螺栓对压电换能器性能参数的影响[J]. 压电与声光, 2010, 32(6): 985-986.

LI Jun, HE Xiping, DING Shaohu. Effect of bolt on the performance parameters of piezoelectric transducer[J]. Piezoelectrics & Acoustooptics, 2010, 32(6): 985-986.

[13] 汪承灏. 夹心式压电换能器的参数对有效耦合系数的影响[J]. 声学学报, 1981, 6(3): 194-197.

WANG Chenghao. The effects of the parameters of the sandwich piezoelectric transducer on the effective coupling coefficient[J]. Acta Acustica, 1981, 6(3): 194-197.

[14] 杨佳婷. 螺栓对压电换能器有效机电耦合系数影响的研究[D]. 西安: 陕西师范大学, 2018.

YANG Jiating. Relationship between the bolt position and the effective electro-mechanical coupling coefficient of a transducer[D]. Xi’an: Shaanxi Normal University, 2018.

Relationship between the bolt position and the effective electro- mechanical coupling coefficient of transducer

YANG Jia-ting, LI Na, WU Ting-ting, HE Xi-ping

(School of Physics and Information Technology, Shaanxi Normal University, Xi’an 710119, Shaanxi, China)

In this paper, the influence of the bolt position, which is in the middle or at the back of a transducer, on the effective electro-mechanical coupling coefficient of the transducer is studied. Considering that the bolt is equivalent to a T typed four-terminal network, the relationship between the effective electromechanical coupling coefficient and the bolt length is analyzed according to the electromechanical equivalent circuit of transducer. The results show that the electromechanical coupling coefficient monotonically increases with increasing the length of the bolt located in the middle of the transducer; however, it increases first and then decreases with increasing the length of the bolt located at the back of the transducer. The variation of the effective electromechanical coupling coefficient with changing the length of the bolt located at the back is more obvious, but its value is all lower than that of the bolt located in the middle, which illustrates that the electro-mechanical coupling performance of a transducer is better for the bolt located in the middle of the transducer.

transducer; bolt; effective electro-mechanical coupling coefficient

O426.2

A

1000-3630(2018)-06-0618-05

10.16300/j.cnki.1000-3630.2018.06.019

2017-11-15;

2017-12-18

国家自然科学基金(11774211)资助项目。

杨佳婷(1990－), 女, 陕西榆林人, 硕士, 研究方向为功率超声。

贺西平,E-mail: hexiping@snnu.edu.cn