基于多普勒特征恢复的声矢量阵鲁棒自适应波束形成方法
殷冰洁
基于多普勒特征恢复的声矢量阵鲁棒自适应波束形成方法
殷冰洁
(昆明船舶设备研究试验中心,云南昆明 650051)
在短快拍、信号导向矢量失配环境下,传统的自适应波束形成方法性能受到影响,对角加载技术是提高算法在复杂环境下性能鲁棒性的重要技术之一。针对水声环境和水声信号特点,提出一种基于声矢量阵的自适应波束形成方法。该方法利用水声信号的多普勒频率信息,在不同环境下自适应地选择最优对角加载因子,确定波束形成的权矢量,从而实现提取期望目标信号、抑制干扰和噪声的目的。无需任何用户参数,鲁棒性强、估计精度高。最后基于声矢量阵进行仿真实验,仿真结果证明了所提出的方法能够有效地获取目标信号,具有较好的抗干扰能力。
自适应波束形成;水声信号;矢量水听器;多普勒特征寻优算法;对角加载技术
0 引言
自适应波束形成在声呐、雷达、通信、射电天文及生物医学工程等领域已经得到了广泛应用[1-3]。然而,水声环境复杂多变,海水温度、风浪和其它环境条件的变化会影响水声阵列的阵形结构,从而给水声信号的自适应波束形成和波达方向估计带来困难。矢量水听器作为一种新型的传感器,由传统的无指向性声压传感器和偶极子指向性质点振速传感器构成,可以测量声场的声压与该处的质点振速,这些信息都有助于改善水声系统的性能,为解决一些水声问题提供了新的思路和方法。
早期的基于声矢量水听器阵列的波束形成算法主要有常规波束形成法(Conventional beamforming, CBF)和最小方差无畸变响应波束形成法(Minimum Variance Distortionless Response, MVDR又称Capon波束形成器)[4],然而,当存在导向矢量误差、阵元校正误差等模型误差时,波束形成器性能受到严重影响[5],而且分辨力由瑞利限决定[6]。瑞利限是波束主瓣的两个零点之间的距离,这个量衡量了阵列分辨两个不同平面波的能力。之后提出的MUSIC方法突破了瑞利限的限制。K T Wong等[7]讨论了基于声矢量传感器阵列的求根MUSIC法,避免了MUSIC方法所要求的噪声子空间的求解。
然而在实际应用中,阵元的幅相误差和位置误差在所难免,尤其对于拖曳阵,阵元位置本来就是时变的,这就导致了导向矢量不准确,加之实际跟踪的运动目标不具备长时间观测的条件,造成了观测数据不充分。在这样的场景下,传统的自适应波束形成方法性能严重下降。因此,如何提升自适应波束形成方法的鲁棒性受到学者们的热切关注。较为经典的鲁棒自适应波束形成算法主要有鲁棒Capon波束形成法(Robust Capon Beamforming, RCB)[8-12]和对角加载鲁棒自适应波束形成法等。RCB方法对导向矢量不确定集进行约束,极大降低了导向矢量误差对算法性能造成的影响,但需要用户参数。对角加载方法则需要根据不同准则选择合适的对角加载因子[13-15],导致了该方法在使用时受到条件限制。
本文从目标信号本身的特征出发来实现鲁棒波束形成,通过利用水声信号的多普勒频率信息,提出一种基于多普勒特征恢复的对角加载因子自动寻优方法,进而提取期望目标信号并抑制干扰信号和噪声。该方法不受导向矢量失配及有限快拍效应的影响,在短快拍条件下,依然具有较好的波束形成性能,而且在闭式区间进行对角加载因子寻优,极大降低了算法的计算复杂度。除此之外,该方法无需任何用户参数。
1 信号模型



2 算法实现
对角加载Capon自适应波束形成器的设计准则为


上述式(4)所描述的问题可用拉格朗日方法进行求解,得到:
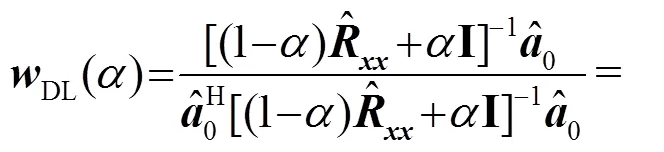

根据多普勒信号的结构特点,当干扰信号被完全抑制且期望目标信号被提取时,有:

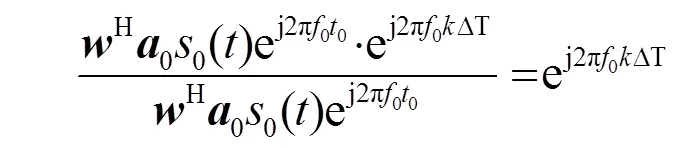

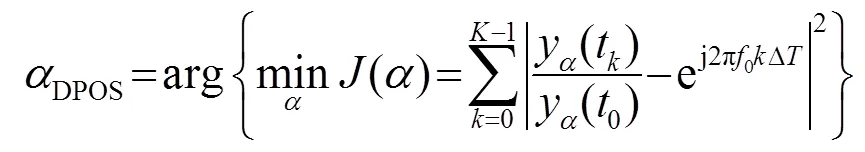
将式(9)代入式(6),得到最优权矢量,表示为
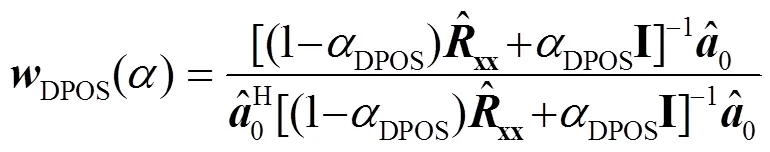
3 仿真实验与性能分析
声呐波束形成器的输出信干噪比(Signal to Interference plus Noise Ratio, SINR)定义为
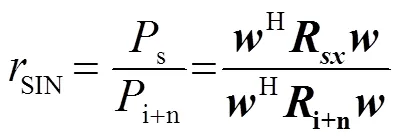

仿真实验1:波束方向图

分析图1和图2可知,本文所提的方法在不同信噪比条件下均能成功抑制干扰,在干扰方向形成很深的零陷,同时波束方向图主瓣对准期望目标信号方向,而传统的Capon波束形成方法则不能成功提取期望信号,在低信噪比的情况下,性能下降更为明显。
仿真实验2:输出信干噪比随信噪比变化曲线


图1 三种方法的波束方向图:快拍数固定为50,信噪比等于0 dB
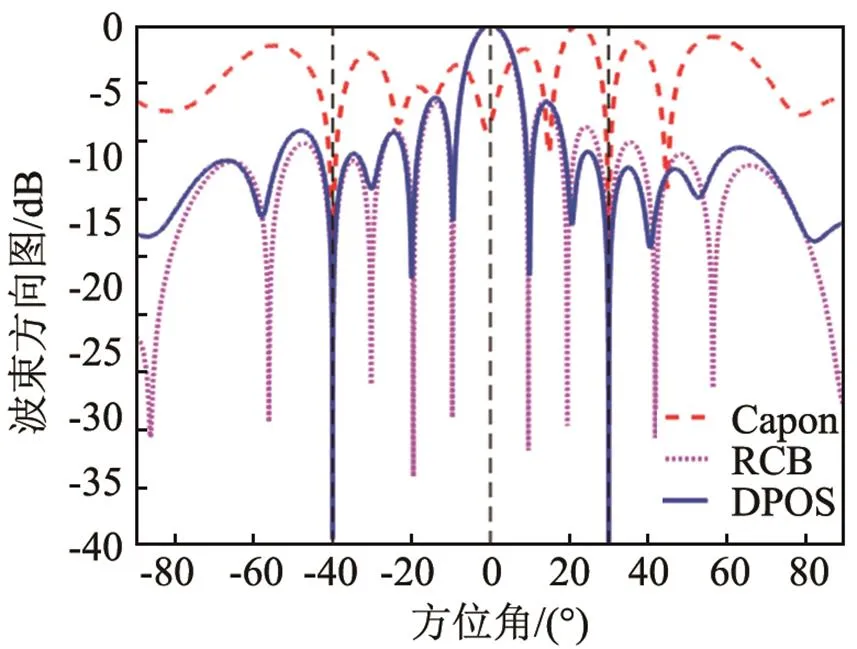
图2 三种方法的波束方向图:快拍数固定为50,信噪比等于15 dB

图3 输出信干噪比随信噪比变化的曲线:快拍数固定为50
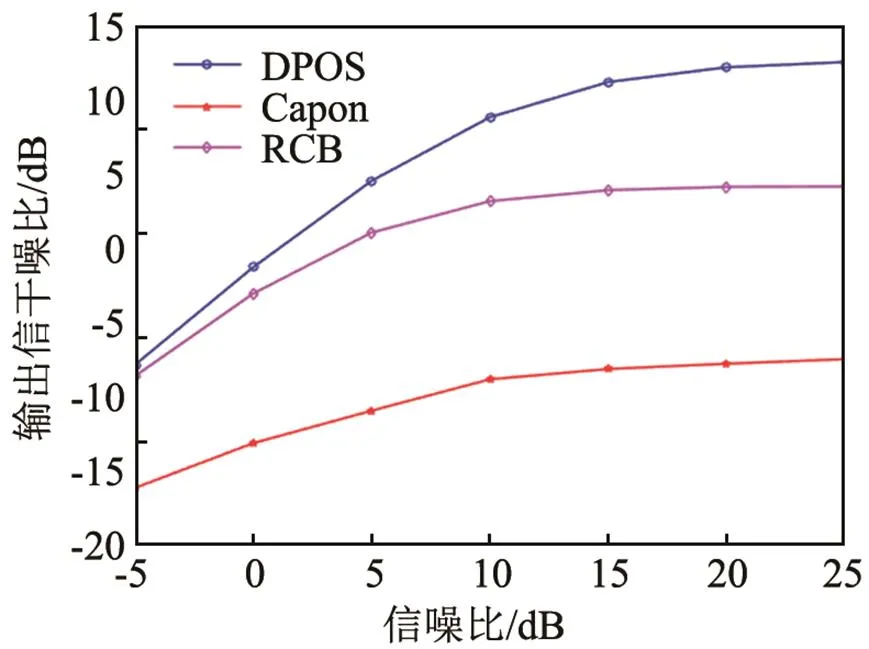
图4 输出信干噪比随信噪比变化的曲线:快拍数为200
仿真实验3:输出信干噪比随快拍数变化曲线
本实验旨在验证所提方法在面对导向矢量误差时的有效性。本实验中,信噪比固定为10dB,导向矢量误差为2°。图5和图6分别为信噪比等于0 dB和20 dB时的输出信干噪比变化曲线。图5和图6的仿真结果显示,DPOS方法在存在导向矢量误差时具有很好的鲁棒性,算法性能仍优于其它与之比较的方法,在短快拍环境下,算法性能尚未受到明显影响。

图5 输出信干噪比随快拍数变化的曲线:信噪比固定为0 dB
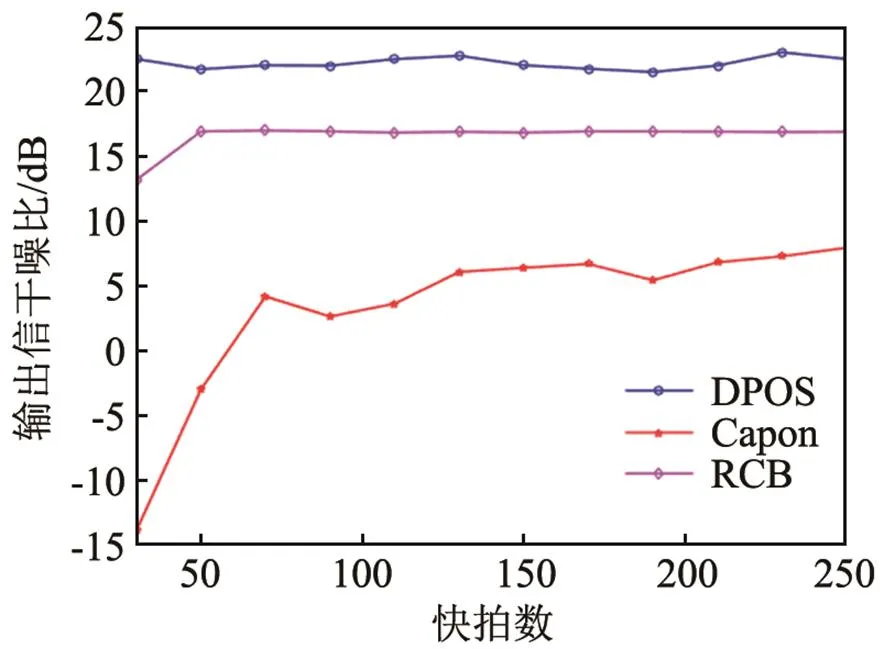
图6 输出信干噪比随快拍数变化的曲线:信噪比固定为20 dB
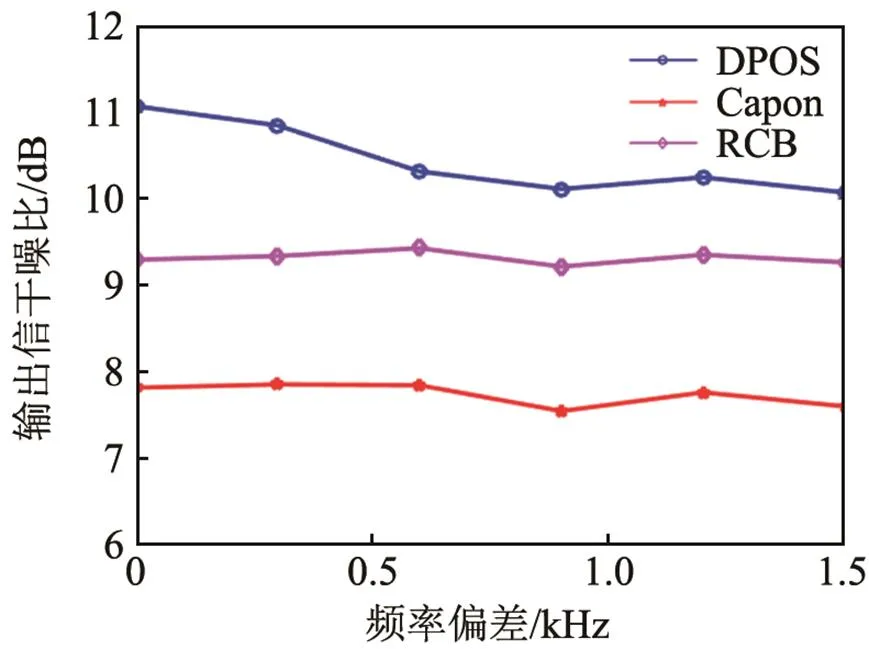
图7 输出信干噪比随频率偏差变化的曲线:信噪比固定为15 dB,快拍数为500
仿真实验4:输出信干噪比随频率偏差变化曲线
本实验研究传感器采样导致的多普勒频率偏差对算法性能的影响,图7为输出信干噪比随多普勒信号频率偏差变化的曲线。信噪比固定为15 dB,采样点数=500。由图7可见,随着频率偏差的增大,各算法性能均有所下降,但是文中所提的DPOS方法仍然有高于其余算法的输出信干噪比,说明DPOS方法具有优于其余算法的期望信号提取能力和干扰噪声抑制能力。
4 结论
本文从水声信号本身的特征出发,给出了一种利用信号多普勒特征进行对角加载因子自适应寻优的鲁棒波束形成方法。该方法充分利用了多普勒信号本身的特点,无需任何用户参数和训练数据;此外,该方法在闭式区间进行对角加载因子自适应寻优时,极大降低了算法的计算复杂度。仿真结果表明,DPOS方法不受导向矢量失配及有限快拍效应的影响,在短快拍条件下,依然具有优于RCB和Capon方法的输出性能,能较好地实现期望信号的提取和干扰噪声的抑制,具有重要的理论意义和应用价值。
[1] ELNASHAR A, ELNOUBI S M, ELMIKATI H A. Further study on robust adaptive beamforming with optimum diagonal loading [J]. IEEE Transactions on Antennas Propagations, 2006, 54(12): 3647-3658.
[2] 许光, 周胜增. MVDR自适应波束形成技术在水声中的研究进展 [J]. 声学技术, 2014, 33(6): 554-558. XU Guang, ZHOU Shengzeng. Development and application of MVDR adaptive beamforming technique in underwater acoustic[J]. Technical Acoustics, 2014, 33(6): 554-558.
[3] 刘广钟, 夏晓丽. 水声通信中RLS-LCMV波束形成算法的研究 [J]. 现代电子技术, 2011, 34(21): 89-91.
LIU Guangzhong, XIA Xiaoli. Research on RLS-LCMV beam forming algorithm in underwater communication[J]. Modern Electronics Technique, 2011, 34(21): 89-91.
[4] HAWKES M, NEHORAI A. Acoustic vector-sensor beamforming and Capon direction estimation[J]. IEEE Transactions on S ignal Processing, 1998, 46(9): 2291-2304.
[5] MESTRE X, LAGUNAS M A. Finite sample size effect on minimum variance beamformers: optimal diagonal loading factor for large arrays[J]. IEEE Transactions on Signal Processing, 2006, 54(1): 69-82.
[6] VAN TREE L. Optimum array processing[M]. Newyork: John Wiley &Sons Inc., 2003: 48.
[7] WONG K T, ZOLTOWSKI M D. Root-MUSIC-based azimuth elevation angle-of-arrival estimation with uniformly spaced but arbitrarily oriented velocity hydrophones[J]. IEEE Transactions on Signal Processing, 1999, 47(12): 3250-3260.
[8] LI J, STOICA P, WANG Z S. On robust Capon beamforming and diagonal loading[J]. IEEE Transactions on Signal Processing, 2003, 51(7): 1702-1715.
[9] LI J, STOICA P, WANG Z. Doubly constrained robust Capon beamformer[J]. IEEE Transactions on Signal Process, 2004, 52(9): 2407-2423.
[10] VOROBYOV S, GERSHMAN A B, LUO Z-Q. Robust adaptive beamforming using worst-case performance optimization: A solution to the signal mismatch problem[J]. IEEE Transactions on Signal Processing, 2003, 51(2): 313-324.
[11] STOICA P, LI J, TAN X. On spatial power spectrum and signal estimation using the pisarenko framework[J]. IEEE Transactions on Signal Processing, 2008, 56(10): 5109-5119.
[12] VOROBYOV S A. Principles of minimum variance robust adaptive beamforming design[J]. Signal Processing, 2013, 93(12): 3264- 3277.
[13] RÜBSAMEN M, GERSHMAN A B. Robust adaptive beamforming using multidimensional covariance fitting[J]. IEEE Transactions on Signal Processing, 2012, 60(2): 740-753.
[14] DU L, LI J, STOICA P. Fully automatic computation of diagonal loading levels for robust adaptive beamforming[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(1): 449-458.
[15] YANG J, MA X C, HOU C H. Automatic generalized loading for robust adaptive beamforming[J]. IEEE Signal Processing Letters, 2009, 16(3): 219–222.
Doppler feature restoration based robust adaptive beamforming for acoustic vector-sensor array
YIN Bing-jie
(Kunming Shipborne Equipment Research and Test Center, Kunming 650051,Yunnan,China)
According to the characteristics of underwater acoustic environment and signals, a diagonal loading adaptive beamforming method based on the vector hydrophone array is proposed for the purpose of improving the robustness of the traditional adaptive beamforming method in the presence of finite sample effect, signal-of-interest steering vector mismatch and/or model array error. This method determines the appropriate diagonal loading level adaptively by using the Doppler information of acoustic signals, then obtains the weight vector to extract the signal-of-interest and suppresses interference signals. Simulation results illustrate the superior performance of the proposed robust user-parameter-free beamformer in the cases of low signal to noise ratio and short snapshot numbers.
adaptive beamforming; acoustic signal; vector hydrophone; Doppler property optimal diagonal level searching(DPOS); diagonal loading
TN911
A
1000-3630(2018)-06-0596-05
10.16300/j.cnki.1000-3630.2018.06.015
2017-08-24;
2017-11-16
殷冰洁(1992-), 女, 云南楚雄人, 硕士, 研究方向为水声信号检测与处理。
殷冰洁, E-mail: bingjieyin@163.com

