具有时变时滞的T-S模糊系统的稳定性分析

杨佳秀， 张大伟

(山西大学 数学科学学院， 山西 太原 030006)

0 引言

最近几年，T-S模糊系统已经广泛应用在工业、航空、医学等各个领域.由于T-S模糊系统可以有效地逼近实际应用中的非线性系统，因此受到越来越多的关注.目前，T-S模糊系统的研究已经得到了大量的成果，特别是对于时变时滞的T-S模糊系统[1-2].那么，对于一个T-S模糊系统要得到可允许的时延上界来保证系统的稳定性，如何构造合适的Lyapunov-Krasovskii泛函(LKF)和如何估计LKF关于时间的倒数得到较小保守性的稳定性条件是最基本的两个问题，也正是本文的研究目的.

Tian E等[3]通过使用自由矩阵方法来得到稳定性判据.而Li L等[4]通过引入一些积分不等式和自由变量改善了Tian E等[3]的结果.Kwon O M等[5]利用含双积分项的增广Lyapunov-Kroviskil泛函(LKF)得到较小保守性的结果.Peng C等[6]采用了时滞分割和相互凸组合方法，这种方法与Kwon O M等[5]的方法相比，有更小的保守性.最近，Souza F O等[7]通过使用带有双积分项的部分非正定LKF提出一个新的方法来降低保守性，但是，Souza F O等[7]的方法基于Jensen不等式得到的结果导致了较大的保守性，则为了降低保守性，Feng Z G等[8]提出相互凸组合方法，对上述的问题进行改进，得到较好的结果.同时，研究时变时滞系统的无限维性质时，相比于先前的文献， Seuret A等[9]提出的Bessel-Legendre不等式可以提供一个更可能紧的上界，并且使用Bessel-Legendre不等式时，构造的LKF应该依赖于Bessel-Legendre不等式.因此，如何使用Bessel-Legendre不等式得到使具有时变时滞的T-S模糊系统稳定的较小保守性判据，正是本文的主要工作.

本文也将讨论具有时变时滞的T-S模糊系统的稳定性问题.通过构造一个新颖的合适的增广Lyapunov-Krasovskii泛函(LKF)，并且基于Bessel-Legendre不等式及相互凸组合引理，给出具有时变时滞的T-S模糊系统的一般稳定性条件.相比于先前文章中的Wirtinger不等式[10]、辅助函数积分不等式[11]和自由矩阵不等式[12]等，本文所提出的新的稳定性条件是对它们的推广，并且可以推广到一些常(离散或分布式的)时滞T-S模糊系统中.最后，通过数值例子，能够更直观地看出文中定理的优越性.

1 问题描述

考虑一个具有时变时滞的非线性系统，由下列的T-S模糊时变时滞模型定义：

规则i：

如果θ1(t)是Mi1，…，θp(t)是Mip，则：

(1)

系统(1)中：x(t)∈Rn是状态向量，Ai和Adi是适当维的常数矩阵.在区间[-τ,0]上定义初始函数φ(t).Mip是第i条模糊规则的前件变量θp(t)的模糊集，i∈{1,2,…,r}是模糊规则的个数.τ(t)是时变时滞函数，满足下列关系：其中，τ和μ都是正常数.

(2)

通过中心加权反模糊化，乘积推理和单点模糊化，可以将系统(1)表达为T-S模糊系统：

(3)

系统(3)中：λi(θ(t))为Mip的隶属度函数，

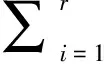
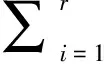
引理1[13]对于给定的整数N≥0,一个实对称正定矩阵R，两个标量a和b,且b>a,和一个向量值微分函数ω:[a,b]→n，则下列不等式成立：

(4)

式(4)中：

(5)

(6)

RN∶=diag{R,3R,…,(2N+1)R}

(7)

ϖN∶=col{ω(b),ω(a),δ1,δ2,…,δN}

(8)

(9)

引理2[14]令T1,T2∈(p×p)是实对称正定矩阵，ϖ1,ϖ2∈p,α∈(0,1).对于任意X1,X2∈(p×p)，下列不等式成立：

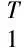
(10)

2 稳定性分析

假设时变时滞τ(t)函数满足条件(2)，在这种情况下，通过使用标准积分不等式分析T-S模糊系统(3)的稳定性.在此，定义：

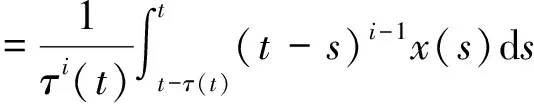
(11)

(12)

定理1对于给定的标量τ和μ，在条件(2)下系统(3)是渐近稳定的，如果存在实对称正定矩阵PN,Q1,Q2,R和适当维数的矩阵Y1N和Y2N使得对于任意的τ(t)∈{0,τ} 有下面的不等式成立：

(13)

(14)

式(13)、(14)中：

C11Ni∶=col{e1,e2,e3,τ(t)e6,…,τ(t)eN+5,

(τ-τ(t))e(N+6),…,(τ-τ(t))e2N+5}

C21Ni∶=col{e1,e2,e3,e6,…,eN+5}

C31Ni∶=col{e1,e2,e3,eN+6,…,e2N+5}

ϑ11,…,ϑ1N}

C32Ni∶=col{(τ-τ(t))ADi,

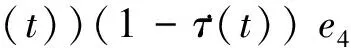
(τ-τ(t))e5,ϑ21,…,ϑ2N}

ADi∶=Aie1+Adie2,ε1Ni∶=col{e1,ADi}

ε3Ni∶=col{e3,e5},ε2Ni∶=col{e2,e4}

LN∶=col{l1,l2,…,lN},lj∶=col{l1j,l2j}

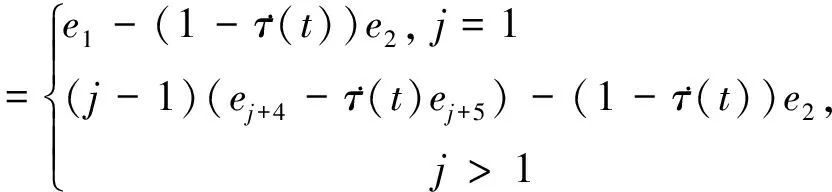
Γ1N∶=ΘNΛNcol{e1,e2,e6,…,eN+5}

Γ2N∶=ΘNΛNcol{e2,e3,eN+6,…,e2N+5}

ei∶=[(0n×(i-1)nIn0n×(N+5-i)n],(i=1,…,N+5)

证明：构造Lyapunov-Krasovskii泛函如下所示：

(15)

(16)

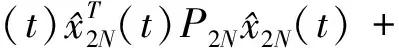
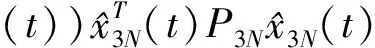
(17)

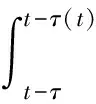
(18)

(19)

式(16)、(17)、(18)中:

τ(t)φ(t),(τ-τ(t))ψ(t)}

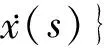
φ(t)∶=col{φ1(t),φ2(t),…,φN(t)}

ψ(t)∶=col{ψ1(t),ψ2(t),…,ψN(t)}

对V(t,xt)求导，得：

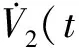
定义：

η(t)∶=col{x(t),x(t-τ(t)),x(t-τ),η1(t)}

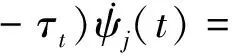
(j=1,2,…,N)

因此，Lyapunov函数(15)式的导数可被改写为：

(20)

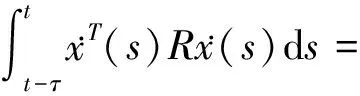
(21)

然后，使用引理1对式(21)进行估计，则有：

(22)

(23)

根据引理2 ，对式(22)、(23)中的凸组合项进行处理，可以得到：

(24)

式(24)中：α∶=τ(t)/τ.最后，联立 (20)、(24)式有：

(25)

定理2给定时滞系统(3),可允许时延满足式(2)，如果存在正整数N0，使得定理1的线性矩阵不等式满足N0，那么证明同样的线性矩阵不等式满足所有的N≥N0.

3 数值例子

在这一节提出一个数字例子证明定理1的有效性.现考虑T-S模糊系统(3)，其中系统矩阵如下：

隶属函数为：

λ2(θ(t))=1-λ1(θ(t)),θ(t)=x1(t)

应用定理1，在这里令μ=0.1，利用Matlab中的Yalmip工具箱求得当N={1,2,3}时的最大允许时延上界.文献[8]中τ(t)的最大允许上界与定理1得到的最大允许上界列于表1中.很容易得出本文所提方法比上述文献有较低的保守性.

表1 μ=0.1，τ(t)的最大允许时延上界

在初始条件φ(t)=[1.5 1]T下，在图1、2中给出了τ(t)=2.2+0.1sin(t),τ(t)=2.623 8+0.1sin(t)的系统轨迹图，以此证明所考虑的系统对于任意时延在τ≤2.623 8时是渐近稳定的，但随着时延允许范围的增大，系统稳定所需要的时间也越长.

图1 τ(t)=2.2+0.1sin(t)

4 结论

本文讨论了具有时变时滞的T-S模糊系统的稳定性分析问题.构造了一个依赖于标准Bessel-Legendre不等式的合适的增广Lyapunov-Krasovskii泛函，提出带有时变时滞的T-S模糊系统渐近稳定的充分条件.这种方法是对基于先前文章中的不等式得到的稳定性判据的一个推广，也有了明显的改进，从仿真例子中可得知.并且，这组线性不等式条件形成了一个分层，也就是随着Legendre不等式N的阶数的增大，能有效改善结果的保守性.