数字摄影测量系统在建立数字地面模型中的实验原理探索

贺翩

(江西中煤建设集团有限公司，江西 南昌 330000)

1 实验原理

1.1 共线方程

摄影影像是空间被摄物体的中心投影。因此，像点、摄影中心和物点共线。共线条件在数学上表示为中心投影构像，其相关的概念、表示及相关应用如下：

(1)概念及表示。共线条件方程：表示像点和物点的中心投影变换方程式。表示如下：

(1)

1.2 共面方程

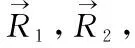
(2)

1.3 影像的内定向

影像内定向，必须量测影像上框标点的影像架坐标或扫描坐标，然后根据量测相机的检定结果所提供的框标理论坐标，用解析计算方法进行内定向，从而获得所量测各点的影像坐标。如果所量测的框标构像的仪器坐标或扫描坐标为(x′，y′)，并已知它们的理论影像坐标为(x，y)，内定向通常采用多项式变换公式，用矩阵表示的一般形式为：x=A′x′+t。

2 双向立体测图原理

2.1 立体像对的相对定向

像对的相对定向无论是模拟法或是解析法，还是数字摄影测量，都是以同名射线对对相交即完成摄影时三线共面的条件作为解求的基础。连续相对定向通常假定左方影像是水平的或其它方位元素是已知的，即可用把共面方程中的X1、Y1、Z1视为已知，且By≈Bx.u,Bz≈Bx.v,此时相对定向元素为右影像的三个角元素φ、ω、κ和基线分量有关的2个角元素u、v。因此将共面方程按多元函数泰勒公式展开的办法展开至小值一次项。通过量测5对同名相点坐标，求解上述未知数，按最小二乘原理进行迭代。

2.2 立体模型的绝对定向

对立体模型的绝对定向而言，通过空间相似变换确定需经过3个角度Ф、Ω、Κ的旋转，一个比例尺缩放λ系数和3个坐标ΔX，ΔY，ΔZ方向的平移，才能将模型点的空间辅助坐标变换为空间坐标。

2.3 单像空间后方交会

空间后方交会所采用的数学模型共线方程中观测值与未知数之间是非线性函数关系，为了便于计算，需把非线性函数表达式用泰勒公式展开成线性形式，我们把这一数学处理过程称之为“线性化”。线性化处理在解析摄影测量中经常用到。共线方程(1)进行线性化后的误差方程式一般形式

(3)

式中：x，y为观测值，相应该正数为vx，vy；X，Y，Z为地面点的坐标；XS，YS，ZS，φ，ω，κ，f，x0，y0为待定参数，(x)，(y)是地面点的坐标视为观测值引入改正数。

2.4 立体像对的空间前方交会

立体像对空间前方交会的数学模型：利用共线方程的严格解法：共线方程决定了摄影中心、像点和物点空间严格的关系。由共线方程(1)式可得：

(4)

对左、右影像上的一对同名点，可列出4个上述的线性方程式，而未知数个数为3，故可以用最小二乘求解。若n幅影像中含有同一个空间点，则可由总共2n个线性方程式解求X，Y，Z 3个未知数。这是一种严格的、不受影像数约束的空间前方交会方法，由于是解线性方程组，故也需要空间坐标的初值。

3 结论

以上就是数字摄影测量系统在建立数字地面模型中的实验原理，摄影测量中双像(立体像对)的量测是提取物体三维信息的基础。通过以上原理，我们对数字摄影测量系统在建立数字地面模型有了理论支撑，在Mapmatrix软件环境下通过内定向，相对定向，绝对定向，核线重采样，影像匹配，DEM的生成与编辑，最后生成数字地面模型DOM。