基于犹豫模糊灰关联的通航机场选址评价模型

陈 璐，郑唯唯

(西安工程大学 理学院，陕西 西安 710048)

通用航空作为航空产业重要的一环，因其机动灵活、快速高效、作业项目覆盖行业多等特点，在国际上获得迅猛发展.而我国通用航空才刚刚起步，通用航空的飞机数量由2005年的383架增长至2016年底的2 000余架[1]，远落后于世界先进水平.我国计划到2020年建成500个以上通用机场，加快通用航空机场建设成为通航发展的必然趋势.

因客观事物的不确定性和复杂性使人难以把握，很多事物难以做出准确描述.2010年Torra[2]开创性地提出了犹豫模糊集(HFS)概念，并给出了犹豫模糊集的基本运算法则和性质.2011年，Meimei Xia,Zeshui Xu[3,4]给出了犹豫模糊集的数学形式，提出了一系列犹豫模糊集的距离测度公式及相似性测度.2012年，Zeshui Xu,Meimei Xia[5]基于犹豫模糊熵测度提出了熵权法，基于犹豫模糊距离测度提出了离差最大化方法来确定属性的权重.2015年，Huchang Liao,Zeshui Xu[6]从标准差角度出发定义了犹豫模糊元的犹豫度及相关系数.2016年，谭吉玉，朱传喜等人[7]从群体一致性角度出发构建了群体一致性指数最大化的权重优化模型.灰关联分析(GRA)[8]是通过各备选方案与最优方案间的关联度大小对方案进行排序，因其计算方法简便，在处理离散型数据和多属性决策问题时具有很大优越性.王旭坪等人[9]提出基于改进直觉模糊AHP和灰色关联评价模型.李庆胜，刘思峰[10]将犹豫模糊集与灰集相结合，提出了灰色犹豫模糊集及其灰关联TOPSIS决策方法.

鉴于我国通用航空在部分地区首次试点，并无相关建设经验，使得通航机场选址评价的指标体系权值和部分指标数据难以准确确定，呈现出犹豫模糊数和精确数值相混合的数据类型，因此，构建基于犹豫模糊的灰关联通航机场选址评价模型.

1 通用航空机场选址评价指标体系

影响通用航空机场选址的因素众多，遵循科学性、独立性和层次性原则，根据《通用机场建设规范》(MH/T5026-2012)，借鉴民用机场选址指标，以通用航空机场选址为目标层，考虑运行环境、基础建设、经济条件、服务对象4个二级指标，并筛选出12个三级指标，构建通用航空机场选址评价指标体系如图1所示.

2 基于犹豫模糊灰关联的通航选址评价模型

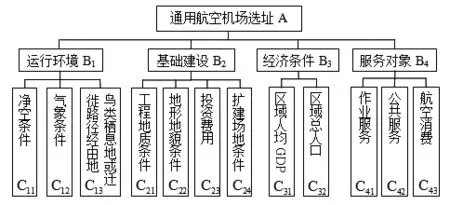
图1 通用航空机场选址评价指标体系

2.1 评价指标权重的确定

由于通用航空处于试点阶段，并无经验数据可以借鉴，设计的专家评价意见表，允许评价数据犹豫，基于犹豫模糊的下级指标对上级指标的重要性程度(隶属度)数据，通过犹豫度函数[7]确定指标权重.通常情况下，若几个专家提供的隶属度值相同时，则只保留一个.而文献[11]指出若只保留一个隶属度值，在两个犹豫模糊元距离的计算中会导致一定误差，且与专家表达的实际意义也有出入.因此，在这里保留专家提供的全部隶属度数据.

犹豫度反映了专家意见的差异大小，信息的差异程度越大，则可靠性就越低，应赋予较小的权重，反之，赋予较大的权重.假设p表示评价指标体系中的一个层次，得到p层指标权重为：

(1)

其中，i表示p层第i个指标，j表示i级指标下的第j个指标，s是p层i下指标j的个数，p,s,i,j∈N+. 集结各层指标权重并作乘积运算，可得p下层指标对目标层的权重，记为ωj，其中，j为指标从左到右的序号.

2.2 构建犹豫模糊灰关联选址评价模型

在一个混合型层次评价问题中，设Ai,i=1,2,…,m为备选方案集，指标权重由上节2.1可得，现对各备选方案进行择优评价.评价信息以犹豫模糊数和精确数值的混合形式给出，得到混合型评价矩阵

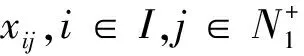
计算步骤如下：

(1)利用2.1提出的方法，确定指标权重.

(2)利用极值法和同向法分别对混合型评价矩阵H中精确值和犹豫模糊数进行数据处理，得到混合型规范矩阵.

效益型指标：

适中型指标：

其中，q为适中值；

(2)

成本型指标：

同向法对H中犹豫模糊数据的处理：

效益型指标：

成本型指标：

(3)

得到混合型规范矩阵：

(3)确定正、负理想方案H+,H-,计算各备选方案分别到正、负理想方案的距离D+,D-，其中，犹豫模糊数之间的距离采用犹豫模糊欧氏距离[4]计算.

确定正、负理想方案H+,H-：

计算各备选方案分别到正、负理想方案的距离D+,D-：

(4)计算各备选方案与正、负理想方案的灰色关联系数：

(4)

(5)

其中，ρ为分辨系数，一般取0.5.得到各备选方案与正、负理想方案灰色关联系数矩阵：

(5)由各备选方案的加权灰关联度计算各方案的相对关联度，据此获得各备选方案的择优排序.

计算各备选方案的加权灰关联度：

(6)

(7)

计算各备选方案的相对关联度：

(8)

从上述计算过程可知，相对关联度越大，方案距离正理想方案越近，方案越优，据此，可获得各备选方案的最优排序，方案Ai较方案Aj优，记为Ai≻Aj.

3 算例分析

设某通航机场选址有6个备选方案(Ai,i=1,2,…,6),运用图1所示的通航机场选址指标体系，C13、C23为成本型指标；3位专家给出的指标隶属度是犹豫模糊数，算例给出的混合型评价矩阵H见表1，其中，C13、C24的属性值是犹豫模糊数，其余是精确值；用MATLAB软件编程，实现对6个备选方案进行评价并择优排序.

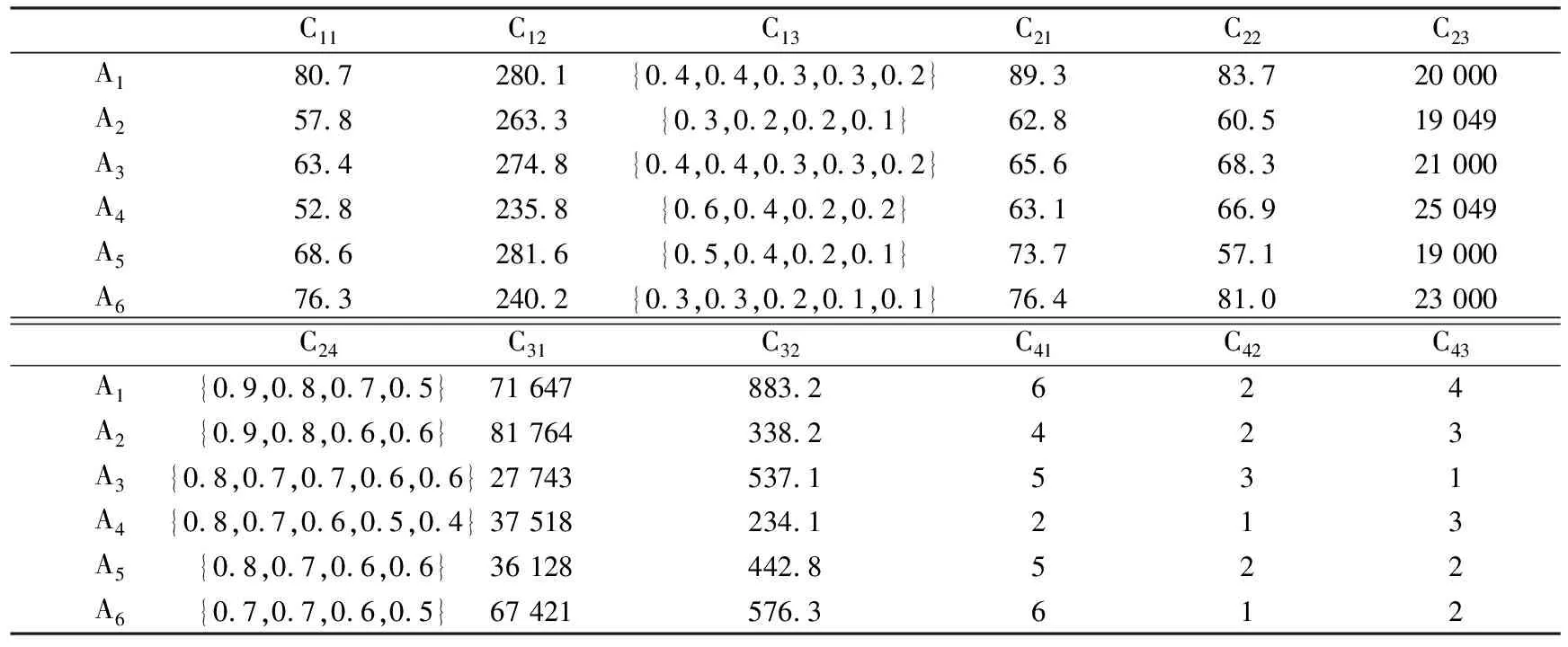
表1 混合型评价矩阵H

算法流程图，如图2所示.

(1)确定评价指标权重.从发放并收回的4份专家意见中，剔除1份数据不完整、不规范的专家意见表，保留其余相对完整的3份专家意见表并汇总数据见表2.

利用公式(1)得到指标权重：

ω1=(0.270,0.262,0.226,0.242),

得到指标层对目标层的指标权重：

ω=(0.092,0.089,0.089,0.065,0.067,0.061,0.068,0.116,0.110,0.079,0.079,0.085).

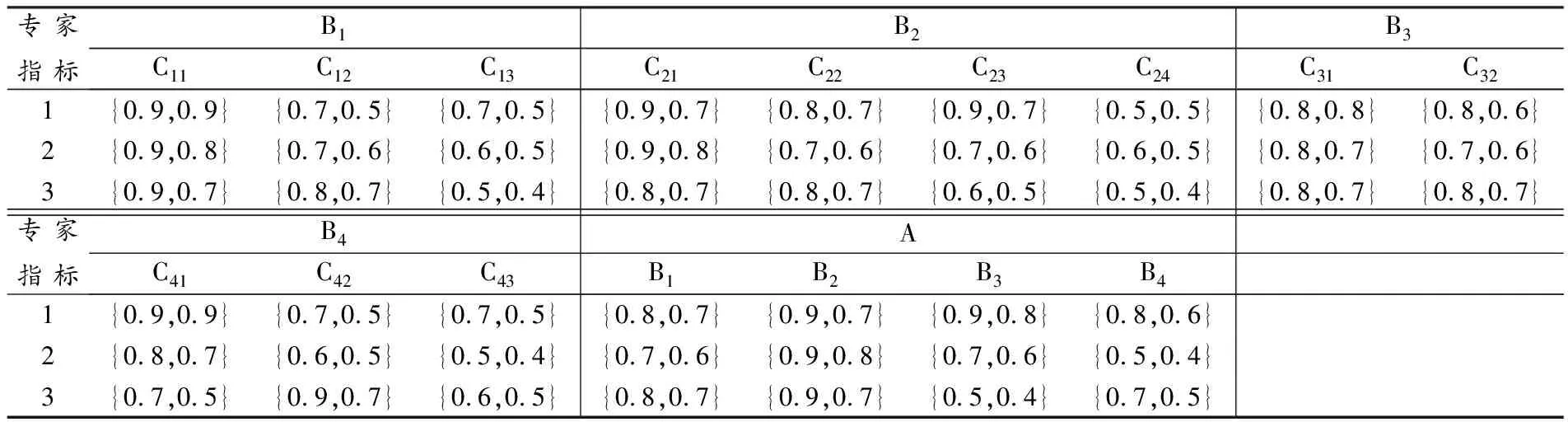
表2 专家意见数据汇总表

(2)利用极值法和同向法，即公式(2)、(3)分别对混合型评价矩阵H进行数据处理，得到混合型规范矩阵H*：

(3)计算正、负理想方案H+,H-及各备选方案分别到正、负理想方案的距离D+,D-(略).

(4)利用公式(4)、(5)，计算各备选方案与正、负理想方案的灰色关联系数，得到方案的灰色关联系数矩阵E+，E-：

(5)利用公式(6)、(7)、(8)，得到各方案的加权灰色关联度及相对关联度：

ξ1=0.697,ξ2=0.516,ξ3=0.484,ξ4=0.335,ξ5=0.511,ξ6=0.531.

依据相对关联度从大到小排序，则6个备选方案的择优评价结果为：A1≻A6≻A2≻A5≻A3≻A4.

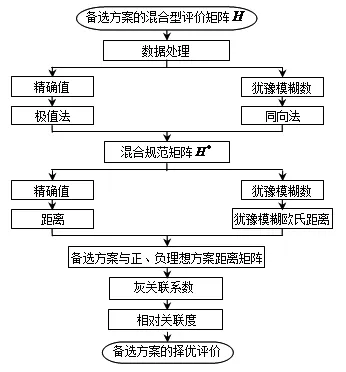
图2 算法流程图

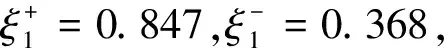
4 结束语

根据通航机场建设规范、民航机场建设指标体系及指标系统的科学规范要求，结合通用航空的特点，构建了通航机场选址评价指标体系；接受专家意见的犹豫模糊数据，给出基于犹豫模糊的指标权值计算方法；对精确数与犹豫模糊数的混合型数据，采用极值法和同向法分别对精确值和犹豫模糊数进行规范化处理；基于灰色关联分析得到各方案与理想方案的加权关联度与相对关联度；依据方案的相对关联度大小得到方案的择优评价及排序.通过通航机场选址算例及MATLAB编程实现并证实了方法的有效性.