两轴速率转台U型架结构设计及有限元分析

安红印

（河北汉光重工有限责任公司，河北 邯郸 056000）

两轴速率转台是导弹及航空航天领域进行半实物仿真和测试的关键设备，它可以模拟飞行器的运动姿态，广泛应用于航空、航天及武器系统中。转台是一种高精度运动仿真和测试设备，它的力学特性的优劣直接影响其仿真和测试精度，是保证航空航天产品以及武器系统性能和精度的基础。因此，在设计阶段对转台U型架进行结构静态和动态特性分析非常重要。

ANSYS软件是融结构、流体、电场、磁场、声场分析于一体的大型通用有限元分析软件，它能与多数CAD软件接口，实现数据的共享和交换，ANSYS软件中得结构分析模块包括静力学分析和动力学分析，动力学分析又包括模态分析、谐响应分析、随机振动分析、响应谱分析、瞬态动力学分析及线性屈曲分析。本文使用ANSYS软件结构分析模块对两轴速率转台U型架结构进行静力学和动力学分析。

1 转台的结构设计

两轴速率转台是集光、机、电一体化的复杂系统。其结构形式多种多样，主要有立式和卧式结构，其他结构都是在这两种结构的基础上衍生出来的。本文研究的两轴速率转台采用立式U-O型结构，即外框架采用U型结构，内框架采用O型结构，该系统采用双轴伺服控制系统，如图1所示是两轴转台的总体结构外形图。U型架是转台的主要结构部件，它有支撑内框及负载的作用，因此U型架要有足够的刚度、强度和尽可能小的转动惯量。

图1 两轴速率转台结构图

2 U型架的静力分析

2.1 静力学方程

结构静力学分析是有限元分析中最基础的分析方法。本文采用Ansys软件对外框架进行静力学分析，所谓静力就是结构受到静态载荷的作用，惯性和阻尼可以忽略，由经典力学理论可知，物体的静力学方程为：

或

式中：[K]——总刚度矩阵；

{x}——节点位移矢量；

N——单元数；

{Ke}——单元刚度矩阵；

{Fa}——支反载荷矢量；

{Fr}——所受总外载荷；

{F}——力矢量。

通过式（1）可以得出{x}，由位移插值函数可以得出单元节点应变和应力的关系表达式：

式中：{ξel}——由应力引起的应变；

[B]——节点上的应变；

{ξth}——热应变矢量；

{σ}——应力矢量；

[D]——弹性矩阵。

求解有限元方程式（4）和（5），即可得出单位各节点相对应的应力。

2.2 U型架网格划分

ANSYS实体模型既可以在ANSYS环境中直接创建，也可以在CAD软件中建模后再导入ANSYS环境下进行分析。本文是在Solidedge中建立实体模型，再将模型导入ANSYS中。两轴速率转台的U型架材料选用铸铝合金（ZL114A），力学性能如表1所示。

表1 ZL1114A力学参数

网格划分的疏密程度直接影响到计算结果的精度，但是网格加密会增加CPU计算时间和需要更大的存储空间。理想情况下的网格密度是其计算结果不再随网格的加密而改变。本例选用单元格尺寸（Element Size）为5mm进行划分,划分后的单元总数为71060个，节点总数为123176个，划分结果如图2所示。

图2 U型架网格划分

2.3 添加载荷和结算结果分析

根据转台U型架的实际受力情况对其进行添加载荷和进行边界条件的约束。添加的载荷主要有：①转台对U型架底面施加的约束，以限制底面的自由度；②U型架的自重和其上加载的负载对U型架施加的压力；③模拟转台在运转状态下产生的惯性力矩。经计算，求解结果如图3、图4所示。

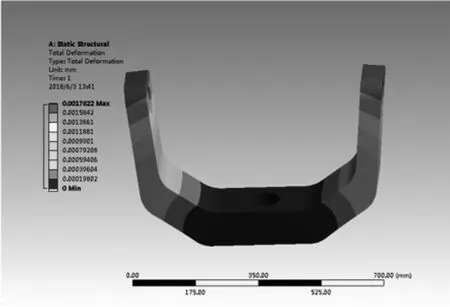
图3 U型架位移变形云图

图4 U型架等效应力云图

由图3可以得出，U型架结构在静力载荷作用下得到的最大位移变形发生在U型架两侧的顶端，且最大位移量为1.78×10-3mm。因仅考虑在静载荷作用下的位移变形，所以变形不大。由图4可知，最大应力区出现在U型架底部棱边处位置，最大应力σmax=0.47M P a，查表得 ZL114A的许用应力[σ]=230MPa,σmax＜[σ],故转台 U型架的结构设计能满足强度要求。

3 U型架得动力学分析

3.1 动力学方程

动力学分析是用来确定惯性和阻尼起重要作用时结构的动力学行为的技术，典型的动力学行为有结构的振动特性，动力学分析可以模拟的物理现象包括：振动冲击、交变载荷、随机载荷地震载荷等。N阶自由度系统的振动微分方程为：

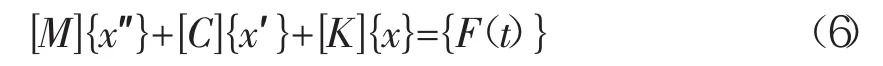
假设为自由振动并忽略阻尼时，其方程为：

结构的自由振动是简谐振动，即位移为正弦函数

将（8）式带入（6）式得

式中：[M]——质量矩阵；

[C]——阻尼矩阵；

{F（t）}——力矢量；

{x＇}——速度矢量；

{x″}——加速度矢量。

式（8）为经典的特征值问题，此方程的特征值为ωi2，其开方 ωi即自振圆频率，自振频率为 f=ωi/2π,特征值ωi对应的特征向量{x}i为自振频率f=ωi/2π对应的振型。

3.2 模态分析

模态分析是计算结构振动特性的数值技术，结构振动特性包括固有频率和振型。模态分析是最基本的动力学分析，也是其他动力学分析的基础，模态分析可以获取结构件的固有频率和振型，从而使结构设计避免共振或者以特定的频率进行振动。ANSYS中有7种模态提取方法，分别为子空间法、动态功率法、分块Lanczos法、缩减法、Power Dynamics法、非对称法和阻尼法，常用的是前4种方法。分块Lanczos法具有收敛速度快等特点，常用在实体单元模型中。本例采用分块Lanczos法进行求解。在对转台U型架精心模态分析时，因为求解的是U型架的固有频率和振型，与所受外力没有关系，所以模态分析时忽略外部载荷的作用。模态分析时施加的约束和网格划分类型应与静力分析时类似。

3.3 计算结果分析

经过计算分析，得到各阶的固有频率和振型云图如图5所示。

从图5中可以看出，一阶模态的固有频率是319.42H z,U型架两侧都沿X轴正方向振动；二阶模态的固有频率是326.36H z,U型架左侧沿X轴正方向振动，右侧沿X轴负方向振动；三阶模态的固有频率是495.2H z,U型架左侧沿Y轴负方向振动，右侧沿Y轴正方向振动；四阶模态的固有频率是495.55H z,U型架两侧都沿Y轴正方向振动；五阶模态的固有频率是974.66H z,U型架两侧绕Y轴向右侧发生弯曲；六阶模态的固有频率是999.33H z,U型架两侧绕Y轴向内发生弯曲。从分析结果可以得出，外框架前五阶的固有频率在319.42～999.33H z范围。在机械系统的设计过程中，一般要求结构的固有频率必须高于其最高工作频率的5～8倍，考虑到有限元分析的固有频率普遍偏高等因素，本文提出了高于机械系统工作频带的10倍要求，而两轴速率转台工作时由外部激励产生的工作频率在10H z左右，远小于外框架的第一阶固有频率319.42H z，所以转台工作时结构本身不会发生共振，设计是可以满足要求的。

4 结论

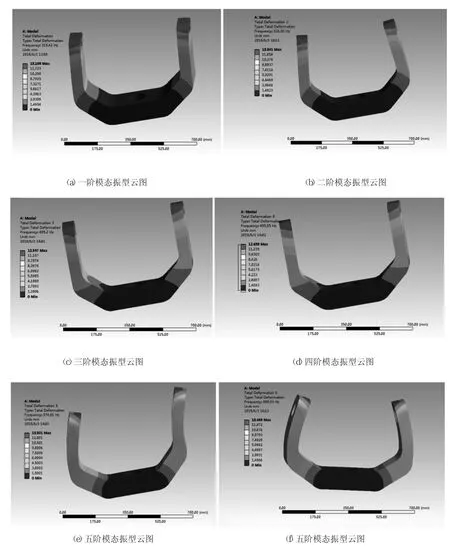
图5 U型架模态振型云图

通过ANSYS软件对U型架静态、模态分析可知，该U型架的设计满足强度和刚度的要求，其动态特性良好，工作时不会发生共振。同时也发现，U型架的结构设计比较保守，可对U型架进行结构优化设计。ANSYS分析计算的结果为结构优化设计提供了重要的理论依据，可让设计者避开结构的共振区间，避免共振的发生，提高机械系统设计的可靠性。