交流伺服式机械压力机用齿轮减速的合理方式探讨

杜 威，赵升吨，范淑琴，刘家骥，高 伟

（西安交通大学 机械工程学院，陕西 西安 710049）

0 引言

机械压力机是锻压生产中重要的设备，传统的机械压力机都带有飞轮，工作时主要依靠飞轮提供锻压所需要的能量，且控制精度低，对减速机构的主要要求是能够达到一定的传动比[1]。与传统机械压力机不同，伺服压力机主要由伺服电机驱动，通过精确控制滑块的运动曲线，获得更好的工件性能，这就要求压力机减速机构等效到电机轴上的转动惯量尽量小，从而获得更好的控制效果。因此伺服压力机取消了传统压力机中惯量大、可储存和释放能量的飞轮，工作时依靠电机的瞬时扭矩来提供滑块需要的压力，因此对伺服电机的扭矩要求比较高，根据工作行程中滑块受到的最大压力、减速机构的传动比和增力比、伺服电机的过载倍数来选择伺服电机的扭矩和功率[2-3]。因为伺服电机的扭矩有限，为了获得较大的吨位，伺服压力机要求减速机构有较大的传动比，同时减速机构的转动惯量尽量小，这样能够更好的发挥伺服电机的优势[4]。

伺服压力机的发展对减速机构提出了更高的要求，在满足传动比和增力比的情况下，减速机构等效到电机轴上的转动惯量要尽量小，目前已经有一些伺服压力机上采用了行星齿轮传动代替传统的外啮合齿轮传动，能够减小伺服压力机减速系统的转动惯量，使伺服驱动系统的加（减）速性能更好，尽可能的发挥伺服压力机的优势[5]。

本文以公称压力为16000kN，公称压力行程10mm，行程次数30次/min，采用一级皮带传动和一级齿轮传动的伺服压力机为例，对其第二级传动分别使用外啮合齿轮和行星齿轮传动进行了设计计算，定量分析了行星齿轮传动相比外啮合齿轮传动的优势。

1 伺服压力机常用减速机构

目前伺服压力机上常用的减速机构主要有以下两种[6]。

1.1 外啮合齿轮减速形式

这种减速形式一般采用一级皮带和一级或两级齿轮传动，传动比约为7～25，如图1所示。

外啮合齿轮传动系统要实现较大的传动比和传递扭矩时，为了满足强度的要求，大齿轮需要很大的体积，用在压力机上时，会占用很大的体积，给压力机减速机构的空间布置带来了很大困难[7]。

1.2 行星齿轮减速形式

和外啮合齿轮传动相比，行星齿轮机构由于行星轮个数多，传递扭矩时同时有多个齿啮合，因此在相同传动比和额定扭矩的情况下，行星齿轮机构的体积通常较小，结构紧凑，方便布置，因此越来越多的在伺服压力机中使用，图2就是一种采用行星齿轮传动的伺服压力机传动系统示意图[8]，为了获得较大的传动比，使用行星齿轮传动时，一般将齿圈固定，太阳轮作为输入，行星架做输出。

图1 采用外啮合齿轮减速的伺服压力机传动系统

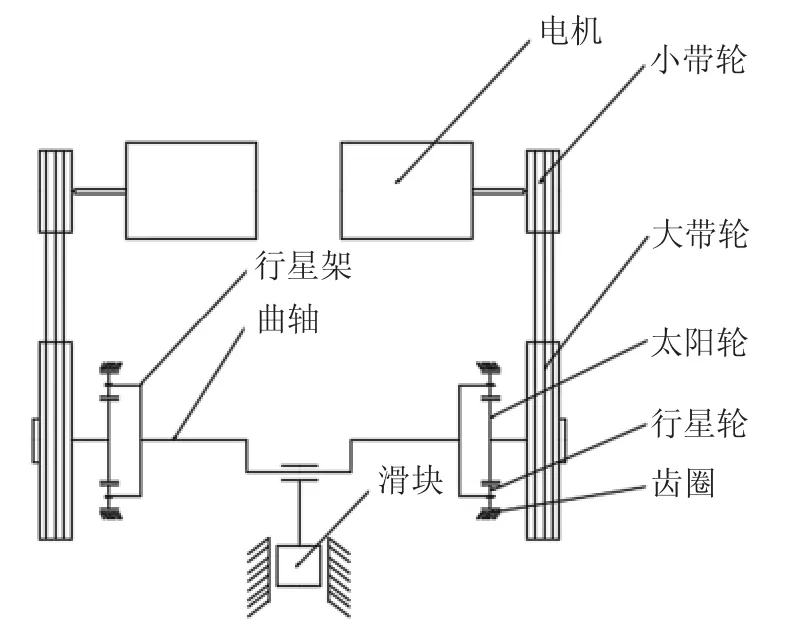
图2 采用行星齿轮减速的伺服压力机传动系统

2 外啮合与行星齿轮传动转动惯量的计算

为了定量比较在相同工况下，外啮合齿轮传动和行星齿轮传动转动惯量的大小，在计算转动惯量时，将齿轮近似看成实心圆柱体，则齿轮绕自身轴线的转动惯量可按下式计算：

式中：J——转动惯量；

Ρ——密度；

B——齿宽；

R——齿轮分度圆半径。

2.1 行星齿轮传动转动惯量计算

设n1为太阳轮转速，n2为内齿圈转速，n3为行星架转速，nP为行星轮自转转速，行星排的转速特性参数为为齿圈的齿数，Z1为太阳轮的齿数，行星齿轮传动的转速特征方程为

将整个机构加上-n3，行星架就固定不动，化为定轴轮系，此时

式中：ZP——行星轮的齿数。

行星齿轮传动时，行星轮在绕着自身轴线自转的同时，又绕着行星排的轴线做公转，因此其转动惯量包括两部分，对自身轴线的转动惯量和对行星排轴线的转动惯量。设太阳轮的转动惯量为J1，行星轮个数为p，自转和公转的转动惯量分别为JP1和JP2，齿圈的转动惯量为J2。假设行星齿轮系各零部件间的摩擦阻力忽略不计，在输入轴作用一个驱动扭矩，驱动扭矩在dt时间内所做的功等于行星齿轮机构的动能增量[9]，即：

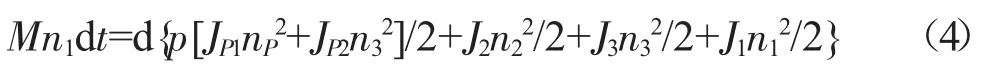
由上式可以得到

设整个机构等效到输入轴的转动惯量为Je，则等效动力学模型为

由上面两式可得到行星齿轮减速机构的等效转动惯量为：

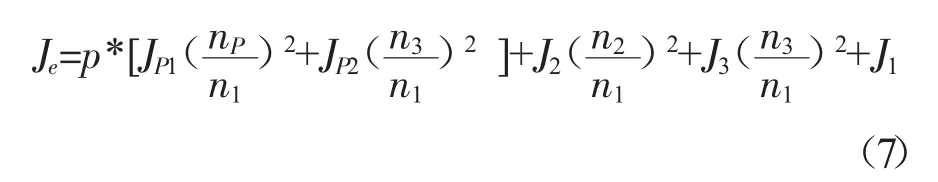
2.2 外啮合齿轮传动转动惯量计算

图3 行星齿轮传动简图

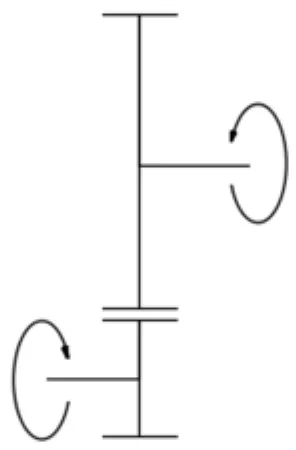
图4 外啮合齿轮传动简图

如图1所示，设n1为小齿轮的转速，n2为大齿轮的转速，J1为小齿轮的转动惯量，J2为大齿轮的转动惯量，R1和R2分别为小齿轮和大齿轮的分度圆半径，根据动力学理论，外啮合齿轮传动等效到小齿轮轴线的等效转动惯量为

3 等扭矩和等传动比条件下外啮合与行星齿轮传动的转动惯量对比分析

3.1 两种传动方式的几何尺寸确定

为了定量比较外啮合齿轮传动和行星齿轮传动转动惯量的大小，本文以采用一级皮带传动和一级齿轮传动，公称压力为16000kN，公称压力行程10mm，行程次数30次/min的伺服压力机为例。其第二级齿轮传动需要传递最大扭矩为50000Nm，传动比为5，根据机械设计手册[10]，对其分别采用外啮合传动和行星齿轮传动进行设计计算，选择20CrMnTi作为齿轮材料，加工精度定为6级，加工后的齿轮需要渗碳淬火处理，其表面硬度可达59～63HRC，其σFlim=340MPa[11]。

最终得到两种传动方式的参数如表1和表2所示。

3.2 两种传动方式的强度校核

为了验证减速机构设计的合理性，分别建立了外啮合齿轮传动和行星齿轮传动的三维模型，并将其导入到ANSYS中进行强度校核，主要校核齿轮啮合处的应力分布，为了简化计算，行星齿轮模型中去掉了行星架，只添加了一个行星轮。两种传动方式的载荷及约束条件设置如下：

外啮合齿轮传动：

（1）在大齿轮内圈施加固定约束；

（2）在小齿轮轴颈处添加圆柱面接触；

（3）在小齿轮（输入轴）施加转矩50000Nm。

表1 外啮合齿轮传动的参数

表2 三行星轮啮合传动的参数

行星齿轮传动：

（1）在齿圈的外圈添加固定约束；

（2）假设行星架固定，在行星齿轮内圈添加转动副；

（3）在太阳轮轴颈处添加圆柱面接触；

（4）行星齿轮载荷分布不均匀系数取1.05，在太阳轮（输入轴）处施加转矩50000/3×1.05=17500Nm[11]。

设置好载荷及约束条件的有限元模型如图5所示。

通过对两种传动方式有限元模型的求解，得到其应力分布云图，如图5所示。

从图5中可以看出，在给定转矩下，等效应力主要集中在齿轮相互啮合处。从图5（a）可以看出，外啮合齿轮传动最大应力在啮合齿的根部，最大值为103.41MPa；从图5（b）可以看出，行星齿轮传动应力最大值为111.8MPa。两种传动方式的最大应力都小于材料的弯曲疲劳极限340MPa，因此强度满足要求，并且两种传动方式在额定工况下最大应力相差小于10MPa，说明两种传动方式适用的工况相近，可以进行对比。

3.3 两种传动方式对比分析

假定采用的行星架结构为单臂式，计算转动惯量时当成一个实心圆柱体。根据第二节的公式可计算出外啮合齿轮传动和行星齿轮传动整体及各部件等效到输入轴的转动惯量如表3、表4所示。

从表3可以看出，外啮合齿轮传动中大齿轮的转动惯量占总体转动惯量的比例达到了96.16%，可见外啮合齿轮传动的转动惯量主要来自于大齿轮。从表4可以看出，行星齿轮传动中，行星轮的转动惯量占总体转动惯量比例最大，达到了63.2%。

图5 外啮合与行星传动的几何模型

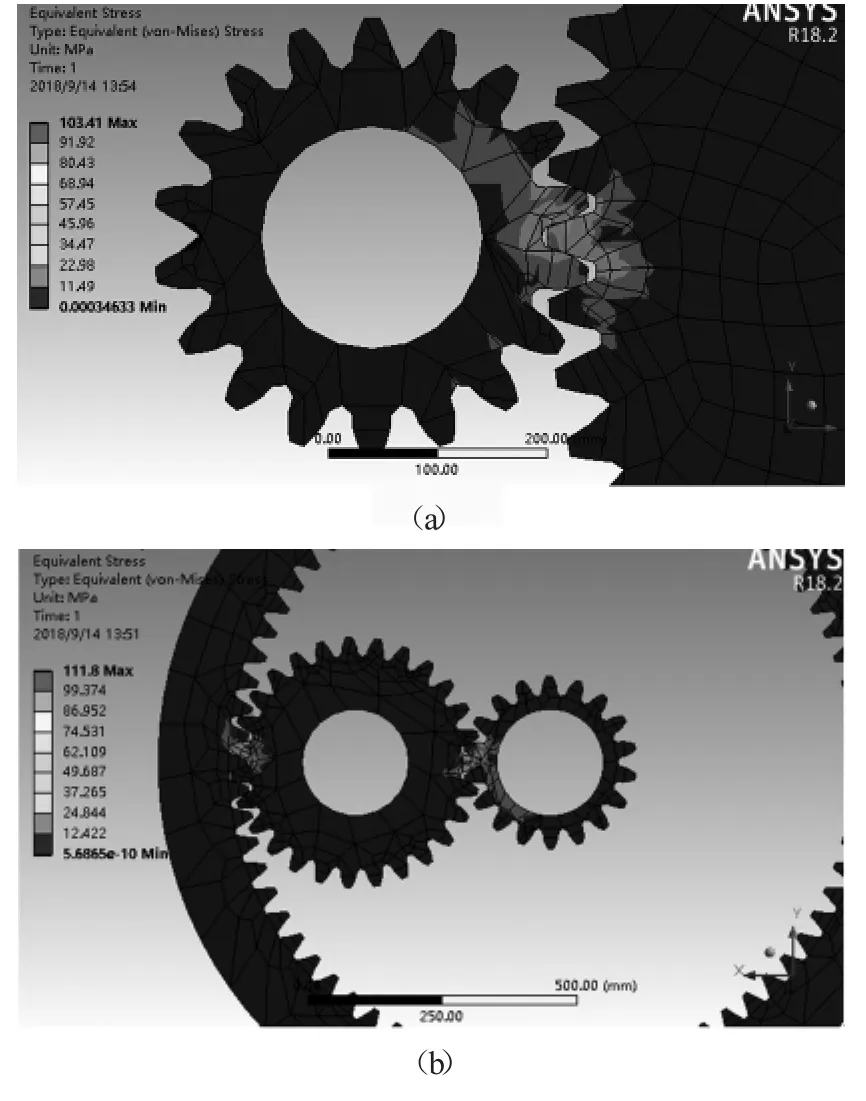
图6 两种传动方式应力分布云图

表3 外啮合齿轮传动的转动惯量

表4 行星齿轮传动的转动惯量

表5 两种传动方式参数对比

假定采用外啮合齿轮传动时，将大小齿轮直径之和作为最大截面尺寸，采用行星齿轮传动时，将齿圈外径作为最大截面尺寸，则可得到两种传动方式的参数对比如表5所示。

从表5可以看出，相同传递扭矩和传动比时，采用行星齿轮传动相比采用外啮合齿轮传动，转动惯量减少了82.36%，质量减少了42.55%，最大截面尺寸减少了41.34%。

4 结论

（1）和外啮合齿轮传动相比，使用行星齿轮传动能够大大减小减速机构的体积、质量和转动惯量。以传动比为5，额定扭矩50000Nm为例，使用行星齿轮传动相比外啮合齿轮传动转动惯量减少了82.36%，质量减少了42.55%，最大截面尺寸减少了41.34%。

（2）伺服压力机为了获得较高的运动控制精度，要求传动系统的转动惯量尽量小，因此相比外啮合齿轮传动，行星齿轮传动更适合用于伺服压力机，并且相比外啮合齿轮传动，行星齿轮传动的体积更小，更加便于压力机减速机构的安装布置。