肘杆式压力机运动学和静力学分析
潘龙飞
(扬州锻压机床股份有限公司,江苏 扬州 225128)
近年来,肘杆式压力机凭借自身结构特点越来越受到市场青睐。与传统曲柄连杆机构相比,肘杆机构具有如下优点:在工作行程阶段获得低而均匀的速度,能保证工件质量;提高滑块空程和回程速度,从而提高生产效率;降低模具与工件的接触速度,有利于提高模具寿命;降低曲柄所承受的扭矩,减小传动机构的零件尺寸和转动件的惯量;用较小的曲柄半径可获得较大的滑块行程,并增大了公称力行程量。
本文以6000kN六肘杆压力机为分析对象,运用机械原理相关知识对其杆系进行运动学和静力学分析,具体说明该结构压力机的特点。
1 杆系分析
1.1 杆系运动简图
由图1所示,该杆系为一六肘杆机构,BD、BE、DE为同一构件,AB杆为主动杆(曲柄),可以绕点A作圆周运动,带动连杆构件BDE摆动,构件BDE的运动又驱动滑块F作上下运动进行锻压加工。建立图1所示坐标系,设AB杆长为L1,其转角为θ1,初始转角为θ10(本文中设为0);BD的长度为L2,其转角为 θ2;BE 的长度为 L4,其转角为 θ4;DE 的长度为 L5,其转角为 θ5;CD 杆长为 L3,其转角为 θ3;EF 杆长为L6,其转角为 θ6;A 点的坐标为(a,-b),F 点的坐标为(0,-s)。

图1 杆系运动简图
1.2 杆系运动参数
6000kN肘杆式压力机的技术参数:公称力Pg=6000kN;公称力行程Sg=7mm;滑块行程S=200mm;行程次数n=40~60spm。
杆系参数:为了既满足使用性能又满足装配结构要求,需对各参数进行筛选,找到最为合适的参数,如表1所示。
2 运动学分析
2.1 求解θ2和θ3
按封闭矢量ABCD分析,写出ABCD的封闭矢量方程式为:

表1 肘杆式压力机的杆系参数

取实部得:

取虚部得:

消去θ2得:

即:

求得θ3后,进一步可求 θ2:
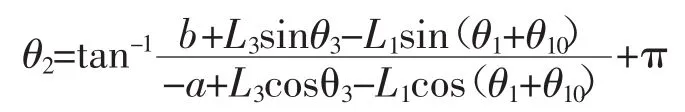
2.2 求解θ5
同理,按封闭矢量BDE分析,写出BDE的封闭矢量方程式为:

取实部得:L2cosθ2+L5cosθ5=L4cosθ4
取虚部得:L2sinθ2+L5sinθ5=L4sinθ4
消去θ4得:

即:

则有:Dsinθ5+Ecosθ5+F=0

2.3 求解θ6和s
同理,按封闭矢量CDEF分析,写出CDEF的封闭矢量方程式为:

取实部得:L3cosθ3+L5cosθ5+L6cosθ6=0
取虚部得:L3sinθ3+L5sinθ5+L6sinθ6=-s
所以:

为了直观表达滑块行程曲线,将式(4)曲线沿Y轴向上平移,使得滑块下死点位移为0,得到图2所示滑块行程曲线。
由图2知,滑块行程 S=200mm,当 θ1=66.6°(即AB杆逆时针旋转66.6°)时滑块到达下死点,当θ1=190.8°时滑块到达上死点,上述角度值表明:滑块从下死点运动到上死点,曲柄旋转了124.2°,滑块从上死点运动到下死点,曲柄旋转了235.8°,由此可推导出此肘杆式压力机具有快返程的结构特点;且由“滑块行程曲线”图可直接看出,滑块在下死点附近停留时间较长,即此肘杆结构下的滑块具有保压的作用。
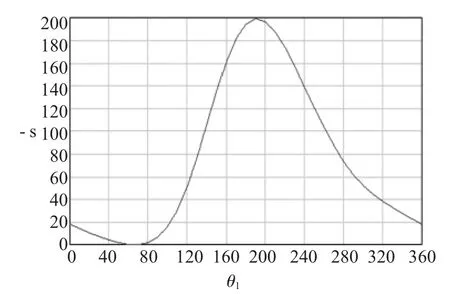
图2 滑块行程曲线
2.4 求解ν和α
根据滑块位移方程,结合压力机行程次数n=40~60spm,假设压力机按最高速运动,即曲柄角速度ω1=2πrad/s(逆时针为正),对式(4)求一次导,即可得到滑块速度曲线;对式(4)求二次导,即可得到滑块加速度曲线:


图3 滑块速度曲线

图4 滑块加速度曲线

由图(3)、(4)知:滑块位于下死点时,速度 ν=0,加速度a=2156.0mm/s2;滑块位于上死点时:速度ν=0,加速度a=-9816.6mm/s2;且滑块作往复运动过程中:最大速度 νmax=1085.0mm/s,最小速度 νmin=-666.7mm/s,最大加速度 amax=7912.7mm/s2,最小加速度amin=-10768.4mm/s2。
另外,当θ1=30.2°时滑块到达公称力发生位置(即公称力行程7mm处),此时,滑块速度ν=-113.4mm/s,滑块加速度a=600.0mm/s2.
3 静力学分析
肘杆式压力机杆系运转时,其各个构件上都受到力的作用,可分为:驱动力、阻力、运动副反力、重力、惯性力。在进行杆系力分析时,为简化计算而不影响工程质量,可根据实际工作条件和希望的计算准确度,只考虑那些解决问题时必不可少的力,而略去一些不重要的力。例如低速机械可以不计惯性力;进行连杆机构力分析时,在近似计算中,可以不计其摩擦阻力;当重力远小于其他各力时,可以忽略不计。本文运用理论力学相关知识,由机床公称力Pg=6000kN,推导曲柄扭矩T的大小。
现将杆系中每个构件简化为二力杆机构,由二力杆性质可知,杆件不是受拉就是受压,规定杆件受拉时为正,受压时为负。分别对B、D、E、F铰链处列静力学平衡方程,推导出扭矩计算公式。
3.1 求解F6
取铰链F列静力学平衡方程(∑Fx=0,∑Fy=0,下同):

求解方程组得:

3.2 求解F4和F5

取铰链E列静力学平衡方程:
求解方程组得:

3.3 求解F2和F3
取铰链D列静力学平衡方程:

求解方程组得:

3.4 求解F1和T
取铰链B列静力学平衡方程:
沿L1杆方向

垂直于L1杆方向

求解方程组得:

假设公称力Pg持续作用整个行程,可得假想扭矩曲线图5,图中可以清晰地看出任一公称力发生位置所对应的扭矩值大小。但压力机实际工作过程中,公称力Pg仅作用于公称力行程范围内,即从公称力行程7mm(即θ1=30.2°)处到滑块下死点(即θ1=66.6°),这段有效的扭矩曲线称为实际扭矩曲线,如图6所示。

图5 假想扭矩曲线图

图6 实际扭矩曲线图
结合图5、图6可知:公称力行程越大,曲柄L1所需提供的扭矩越大,反之,公称力行程越小,曲柄L1所需提供的扭矩就越小;在公称力行程7mm处,曲柄L1所需提供的扭矩大小为56389N·m。
6000KN肘杆式压力机与同吨位曲柄压力机(行程200mm,连杆长度1390mm,公称力行程7mm,最大转速60spm)相比,结果如表2所示。

表2 肘杆式压力机与同吨位压力机比较
4 结论
本文主要对肘杆式压力机进行运动学和静力学分析,详述各运动参数的推导过程,并绘制相关曲线图。由曲线图得出以下结论:
(1)肘杆式压力机在工作区域有较为理想的低速运动特性,模具与工件的接触速度低,有利于提高模具寿命。
(2)肘杆式压力机滑块位移曲线不对称,具有一定的急回特性,可以实现快返程的运动特性,从而提高生产效率。
(3)肘杆式压力机滑块于下死点附近停留时间较长,具有保压作用,保证冷挤压工件的质量。
(4)肘杆式压力机增力效果好,压力机各性能参数相同时,曲柄所承受的扭矩更小。

