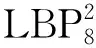基于AdaBoost局部二值模式特征的色织物纹理分类

李鹏飞,闫亚娣,张凯兵,王 珍,朱丹妮

(西安工程大学 电子信息学院,陕西 西安 710048)

0 引 言

由于织物表面是由基本组织结构按照一定的交织规律排列形成，不同的织物具有相异的组织结构，而纹理是描述织物表面的重要属性，具有局部区域不规则，整体区域规律的特点[1].织物种类的繁杂以及织物纹理的多样性和复杂性使得织物纹理在分类方面存在一定难度[2-3].目前对织物纹理的分类主要由人工视觉完成，这种人工视觉的方式不仅耗费大量的人力，且分类效率低[4-5].随着计算机和图像处理技术的发展，传统的人工视觉分类方法已经不能满足当今纺织行业领域的需求，基于图像处理技术的分类方法能够克服人工方法存在的问题，大大提高分类效率和分类准确率.

织物纹理图像的分类一直备受关注，作为织物分析研究领域的重要方面，对于织物纹理分类，早在1996年Barrett等[6]提出了一种基于小波神经网络方法的在线织物分类技术，具有较高的分类正确率，但该方法的数据采集速度较慢，达不到实时性的应用要求；Fan等[7]利用神经网络分类器和降维约减进行织物分类，实验结果表明该方法仅对部分类型的织物有效，且总体分类精度较低；Salem等[8]利用Gabor，支持向量机(SVM)和灰度共生矩阵(GLCM)3种方法对织物纹理进行分析实现自动识别，尽管有较高的识别率，但是SVM仅对平纹图像分类准确率高，而基于GLCM的方法计算时间复杂度较高；Jing等[9]基于纹理特征和概率神经网络(PNN)进行织物结构自动分类，实验结果表明，该方法分类准确率可达95%；之后，又提出了LBP灰度共生矩阵(GLCM)融合的织物组织结构分类方法，由于该方法获取的是织物的全局组织结构，对于纹理结构复杂的色织物分类性能存在较大的局限性[10]；张宏伟等[11]利用深度卷积神经网络进行织物花型分类，该方法具有较高的运算效率，但该方法需要大量的织物样本训练相应的模型，而且不同数量的样本训练得到的模型对分类精度有较大的影响.针对上述分类算法存在实时性较低、识别精度不高以及织物纹理结构存在的多样性等分类问题，本文给出一种基于AdaBoost局部二进值模式(LBP)特征的色织物纹理分类算法,针对织物图像的训练集训练不同的弱分类器，再集合这些弱分类器，构成一个更强的最终分类器，实现了4种类型的织物自动分类.LBP是从织物图像像素的邻域或者局部来描述织物纹理的特征，然后利用AdaBoost算法对织物进行分类.实验结果表明提出的分类算法具有一定的实时性，使得织物纹理的自动识别率更准确.

1 特征提取

1.1 纹理特征提取

纹理的特征提取是进行纹理分类的关键，目前图像纹理特征提取的方法主要有基于统计的方法[12]、基于模型的方法[13]和基于变换域的方法[14].统计的方法主要利用图像灰度直方图的统计矩阵进行提取，典型的分析方法有灰度共生矩阵[15]和方向梯度直方图[16]；基于模型的方法是假设图像为一参数模型，经典的方法有马尔科夫随机场模型[17]和分形模型[18]；基于变换域的方法主要有Gabor变换[19]、小波变换[20]和傅里叶变换[21].

针对织物纹理的局部不相似，全局有规律的特性，文中采用LBP进行织物图像的纹理特征提取，所提取的LBP特征能够获取织物图像的局部和全局纹理特征，并进行有效的分类.

1.2 LBP的实现

LBP是由T.Ojala等[22]于1994年提出的一种描述图像局部纹理的特征算子，具有旋转不变性和灰度不变性等特点，可用于图像特征的分析.经典的LBP算子定义为3×3的正方形窗口，以窗口的中心像素为阈值，将其相邻8邻域像素的灰度值与当前窗口中心点的像素值比较，若邻域的像素值小于中心点的像素值，则将该像素点的值置0，反之置1.比较之后产生一个8位的二进制数，即为LBP码.这样通过计算的LBP码就可反映该窗口的区域纹理特征信息.具体实现过程如图1所示.

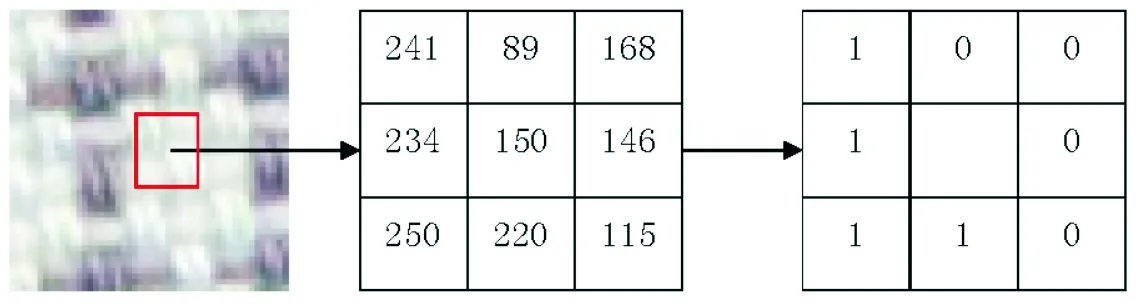
(10000111)10=225图 1 LBP码的形成过程Fig.1 The formation process of LBP code

但是该实现过程只覆盖了一个固定半径范围内的小区域，而且仅仅适用于灰度值的单调变化.为了满足不同尺寸和频率的纹理的需求，将3×3邻域扩展到任意邻域，并用圆形邻域代替正方形邻域，通过改变圆的半径和邻域个数可实现不同尺度和角度的特征分析.实际应用中，为实现旋转不变性，减少特征向量的维数，降低高频噪声带来的影响，定义如下的局部二值计算公式为

(1)

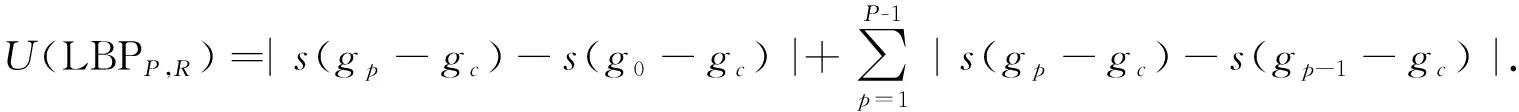
(2)

式中:gp表示邻域像素点的灰度值；gc表示中心像素点的灰度值；P表示邻域集内的采样点数；R表示圆形邻域的半径.不同半径和邻域像素形成的几种LBP算子如图2所示.

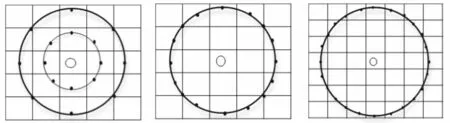
图 2 4种LBP算子Fig.2 Four types of LBP operators

在纹理分类等应用中，将图像划分为若干子区域，对每个子区域内的每个像素点提取LBP特征，然后在每个子区域内建立LBP特征的统计直方图，这样就可以用若干个直方图组来描述整个图像.对于实验中的织物图像进行特征提取时，为了较大程度地获取表征织物结构的特征，同时又不失去织物的细节特征，将输入的50×50图像划分为20×20个子区域，对每一个子区域内的各个像素点提取LBP特征，得到每一幅图像所表示的5 600维的LBP特征.然后对4类织物的400幅图像分别进行LBP特征提取，将得到的所有特征按行排列，即可得到最终400×5 600的特征矩阵作为下一步训练的模型.

2 AdaBoost分类算法

AdaBoost是一种集成迭代的自适应增强算法，能够很好地应用于分类问题.AdaBoost算法通过改变数据的分布，即在分类过程中通过修改样本的权值来实现分类，根据每次迭代中训练集内每个样本的分类正确与否，并参考上次迭代的分类正确率，来更新每个样本的权值.其核心思想是针对同一个训练集训练不同的分类器(弱分类器)，对于前一个弱分类器分错的样本，权值会得到加强，加权后的全体样本再次被用来训练下一个基本分类器，同时在每一轮中加入一个新的弱分类器，直到达到预先指定的迭代次数或者预定的最小错误率，每次迭代结束后，所有的弱分类器融合作为最终的决策强分类器.具体的算法描述如图3所示.

给定一个训练数据集T={(x1,y1),(x2,y2)，…，(xN,yN)},xi表示数据,yi表示数据所属的类．AdaBoos的目的就是从训练数据中学习一系列弱分类器,然后将这些弱分类器组合成一个强分类器．首先,初始化训练数据的权值分布,每一个训练样本最开始时都被赋予相同的权值,即1/N.

(3)

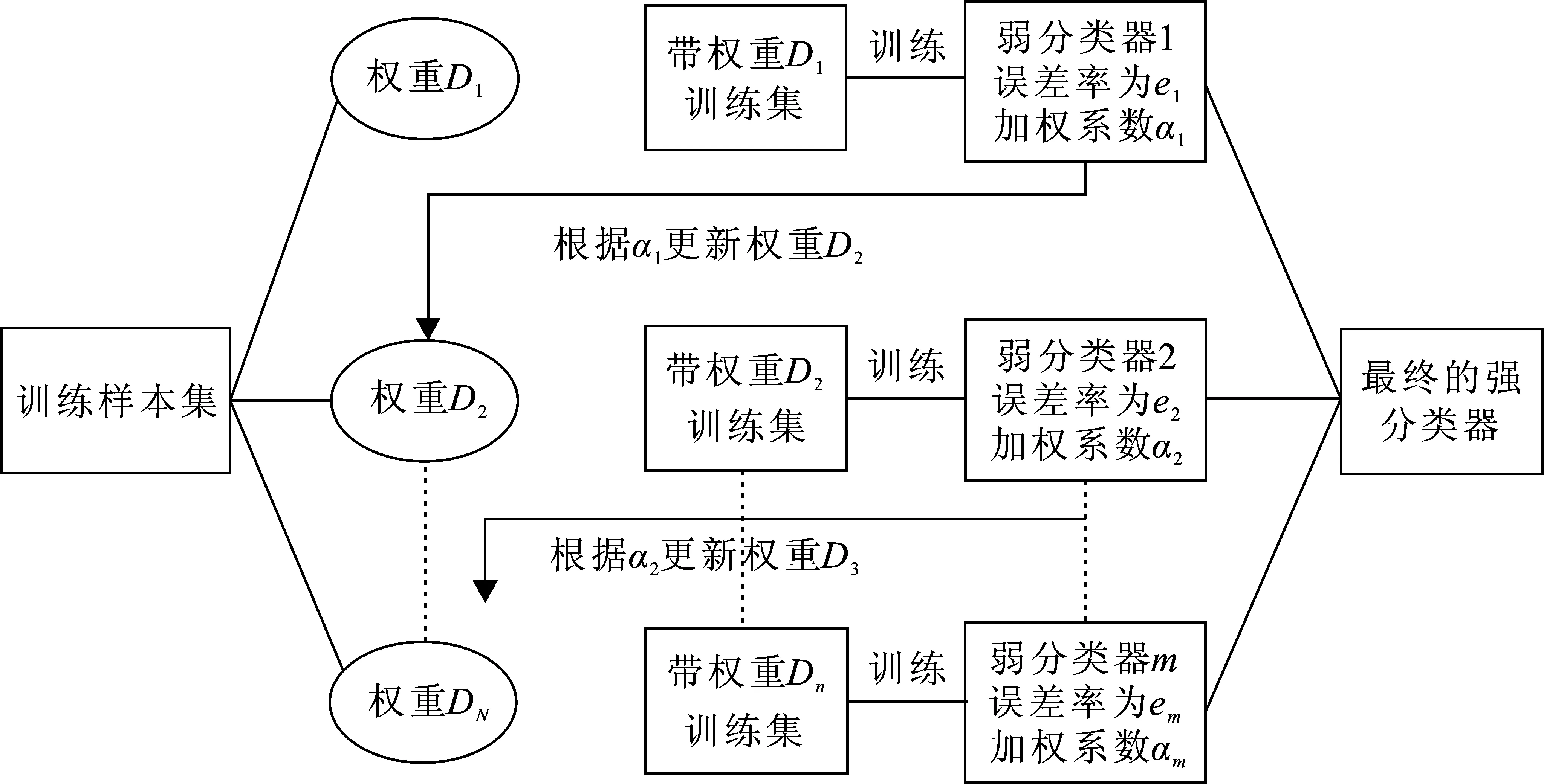
图 3 AdaBoost算法Fig.3 AdaBoost algorithm

进行迭代,用m=1,2,…,M表示迭代的轮数．使用具有权值分布为Dm的训练数据集学习,得到基本的弱分类器:Gm(x):χ→{-1,+1},即分类误差率大于50%的分类器,计算弱分类器Gm(x)在训练数据集上的分类误差率,得

(4)

(5)

更新训练数据集的权值分布,以得到样本新的权值分布,用于下一轮迭代,有

Dm+1=(ωm+1,1,ωm+1,2,…,ωm+1,i,…,ωm+1,N),

(6)

(7)

(8)

式中:Zm是规范化因子,在新一轮的迭代中,被基本分类器错分类的样本权值增大,而被正确分类的样本权值减小．通过这样的方式,AdaBoost方法能够重视错分类的样本,从而在下一轮迭代中分配较大的权重,使得难分的样本可以在新的分类中被正确分类.

组合各个弱分类器,表示为如下的f(x),得

(9)

通过分析可以得到最终的强分类器G(x)，为

(10)

3 实验与分析

此算法运行的软件环境为MATLAB R2014a，系统环境为Windows7和6 GB RAM内存。为了验证本文提出算法的有效性，从TILDA织物纹理图库及CCD相机采集的织物图像数据中选择了1 300幅织物图像进行实验，对其进行分类和预处理操作，将图像分为4类，包含缎纹、斜纹、梭织，其中缎纹由相邻两根经纱或纬纱上的单独组织点均匀分布但不相连续的织物组织，梭织是将纱线由经纬2个方向相互垂直交织而成的布，斜纹采用各种斜纹组织使织物表面呈现经或纬浮长线构成的斜向纹路，这里选择2种不同纹理的斜纹表示为斜纹1和斜纹2，分别标记为“1，2，3，4”.每一类包含100幅大小为50×50的相似纹理结构的织物图像，共400幅图像，部分织物样本如图2所示.对图像进行人工分类和标记，建立训练和测试图像库，其中在每一类图像集中随即选取75%(300幅图像)用于训练，剩余的25%(100幅图像)用于测试.在训练阶段，通过AdaBoost算法建立一个训练模型，在测试阶段用来分类，能够实现织物的自适应和实时分类.

(a) 缎纹 (b) 梭织 (c) 斜纹1 (d) 斜纹2图 4 织物样本Fig.4 The fabric samples

在使用LBP进行织物特征提取时,不同的邻域半径和邻域个数会导致不同的特征表示,实验中比较不同半径R=1,2,2,3对应的邻域像素P=8,8,16,24的LBP特征,以及该参数对应不同弱分类器时的分类准确率,具体的分类结果如表1所示.可以看出,对于相同纹理的织物,取不同邻域半径和邻域像素数时,所提取的LBP特征也是不同,从而建立的分类模型也不同,最后的分类准确率也不同;对于相同的邻域半径和邻域像素数,在不同的弱分类器个数下,分类准确率也不同.从表1的实验数据可以看出,当邻域半径为2,邻域像素为8时,分类的准确率最高为100%;当邻域半径为1,邻域像素为8时分类率在弱分类器为30时分类准确率达到最高,为94%;当邻域半径为2,邻域像素为16时在弱分类器为40时的分类率,最高仅能达到94%,但代价是消耗了更大的计算成本;当邻域半径为3,邻域像素为24时,分类准确率在弱分类器为40时最高可达到96%.根据上述实验结果和考虑识别过程中的计算成本,本文实验中选取的经典算子进行纹理特征的提取.

表 1 不同邻域半径和邻域像素数对应不同弱分类器的分类准确率Table 1 The accuracy rate with different R and P corresponding weak classifiers弱分类器数LBP不同取值准确率/%LBP(1,8)LBP(2,8)LBP(2,16)LBP(3,24)10819791942092989195309410093964092989496

由于LBP特征能够更好地表征织物纹理特性，为了证明LBP在织物纹理特征表征上的有效性，实验中对比了Gabor特征表示[19]、方向梯度直方图(histogram oriented gradient,HOG)特征表示[16]和本文提出的LBP特征表示在AdaBoost分类器上的准确率.具体的

表 2 不同特征表示的AdaBoost算法的分类精度Table 2 The classification accuracy of AdaBoost algorithm represented by different features

结果如表2所示, Gabor特征表示的AdaBoost分类准确率最高为75%，分类的准确率较低；HOG特征表示的AdaBoost分类在梭织和斜纹2上能够达到较高的准确率；而提出的LBP特征表示在实验的4类织物上都可达到较高的分类准确率.

为了评价提出的AdaBoost分类算法的性能，使用分类的正确率作为评价标准.其中分类的正确率y表示准确分类的样本数目与参加分类的总样本数的比值，实验中有4类织物，每类均有100幅图像，其中随机选取的75%作为AdaBoost训练样本，其余的25%作为测试样本.通过式(11)可得到分类的准确率.

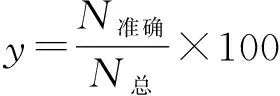
(11)

表 3 不同弱分类器数目下的分类 精度和运行时间Table 3 The classification accuracy and CPU Time in different numbers of weak classifier

式中：N准确表示正确分类的样本数目；N总表示进行分类的总样本.实验通过设置不同个数的弱分类器进行迭代，训练出不同的弱分类器，建立基于AdaBoost自动分类的模型，对随机选取的测试样本进行分类，具体的分类精度如表3所示.由表3可以看出，当训练的弱分类器的个数较少时，准确率较低，但是节约了运行时间，经过比较发现，弱分类器的个数为10时，分类的准确率仅仅86%，运行时间也相应地减少为194 s；当弱分类的数目达到30时，对错分样本的重视程度更高，在下一轮训练中，再次对错分样本进行训练，这样错分样本在更多次的训练中，权重增加；但是并不是弱分类器数目越大越好，当弱分类器个数过大时，CPU运行时间会成倍地增加，而分类精度的提升很小，这是因为错分的样本权重不可能无限地增加，所以实验中选择弱分类器即迭代次数为30进行训练.

为了进一步评价该分类算法的优劣，本文利用混淆矩阵和ROC曲线判定AdaBoost算法的分类性能.混淆矩阵也称为错误矩阵，矩阵的每一列表达了分类器对于样本的预测比例，每一行的数据总数代表了该类被分类的百分比.而ROC曲线是反映敏感性和特异性连续变量的综合指标，横坐标表示分类的假正率，纵坐标表示分类的真正率.

图 5 混淆矩阵Fig.5 Confusion matrix

图5是4种类型的织物纹理基于AdaBoost的分类结果.在该混淆矩阵中，斜对角线上的数据表示每一类织物分类的百分比.从图5可以看出，该分类算法对于第2类织物能完全分类，第4类织物也有较高的分类率.其中0.12表示第3类织物被错分为第1类的比例，0.04表示第4类被错分为第1类的百分比.可以得出，提出的基于AdaBoost织物纹理分类算法是有效可行的.

图6是4种类型织物分类的ROC曲线，在ROC曲线中，RFP(假正率)是作为X轴表示被预测为正的负样本结果数与负样本实际数的比值，RTP(真正率)作为Y轴是正样本预测结果数与正样本实际数的比值，表示式为

RFP=FP/(FP+TN)，

RTP=TP/(TP+FN).

式中：FP是假正，指被模型预测为正的负样本；TN是真负，指被模型预测为负的负样本；TP是真正，指被模型预测为正的正样本；FN是假负，指被模型预测为负的正样本.图6中红色曲线R为对每一类的每个样本的分类率，绿色曲线B为模拟的平滑曲线，当分类曲线越靠近坐标位置的左上角，即坐标1，分类的精确度就更高.从图6可以看出，对于进行分类的4种样本，梭织类和斜纹2的曲线更靠近坐标的左上角位置，相应的分类率也高，而斜纹1和缎纹类相应的准确率较低.通过综合分析，所提出的AdaBoost分类算法有很好的分类性能，对每一类织物的分类真正率都更接近1，假正率基本为0，即该分类器错分样本的能力很低.

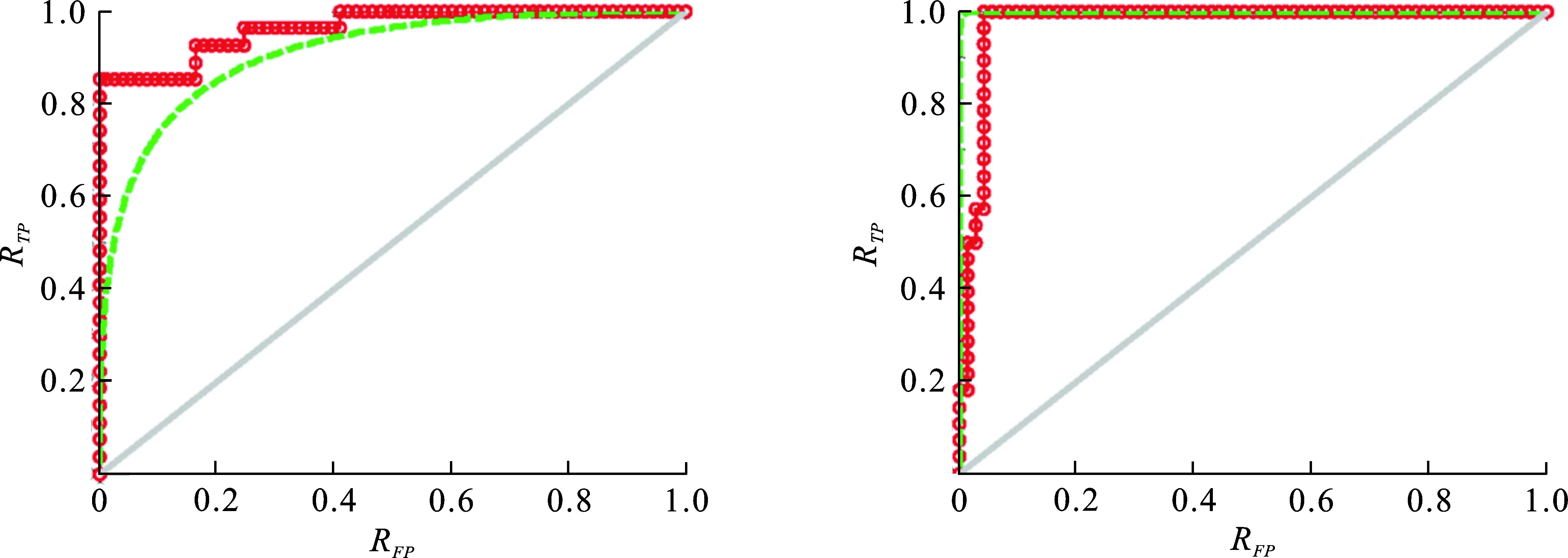
(a) 缎纹 (b) 梭织

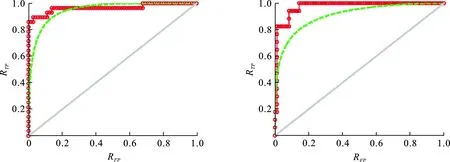
(c) 斜纹1 (d) 斜纹2图 6 ROC曲线Fig.6 ROC curves

4 结束语