基于主惯导参数特性的传递对准调平方法

杨管金子, 李建辰, 黄 海, 国琳娜



基于主惯导参数特性的传递对准调平方法

杨管金子, 李建辰, 黄 海, 国琳娜

(中国船舶重工集团公司 第705研究所, 陕西 西安, 710075)

初始对准时间作为一项重要指标, 直接关系到鱼雷在战场上的快速准备性能。传统对准算法及调平判据由于其内部参数一般固定不变, 一方面使得对准时间过长, 另一方面针对不同对准工况的适应性较差。文中提出一种基于主惯导速度注入参数和水平姿态角晃动参数特性的对准调平方法, 采用BP神经网络对该特性进行辨识, 实时自适应对内部特定参数进行在线更新, 在保证对准精度的同时, 以达到较快的滤波器收敛速度和不同工况下的及时调平判定。对比试验结果表明, 该方法能够有效地加快失谐角收敛速度, 且根据不同工况自适应设计调平判据, 可达到缩短初始对准时间的目的。

鱼雷; 主惯导参数; 传递对准; 调平判定; BP神经网络;

0 引言

鱼雷作为重要的反舰反潜水下战术武器, 在复杂多变的战争环境中, 其需要具备快速反应能力。随着技术的发展、战争快速性及多变性的升级以及战术指标的提高, 各国海军也逐步需要鱼雷具备更加敏捷的战场应变及机动能力。其中, 初始对准过程占据了大部分的射前准备时间, 成为鱼雷研制中的一项重要指标。

装载于水面舰或潜艇等平台的常规鱼雷, 其射前对准环境随着平台机动及风浪或洋流干扰形成动基座。在此条件下, 针对初始对准技术的研究, 一般着眼于对滤波算法的选择及改进, 但不同的滤波算法最终定位于采用自适应的方式对量测噪声进行在线估计, 以提高对准精度以及缩短对准时间, 研究结果表明, 以上方法相比较标准Kalman滤波而言在一定程度上能够提高滤波的收敛速度, 但并未对对准结束时刻进行明确说明[1-3]。国内外可检索到的针对调平判定方法的文献非常少。

考虑到从主惯导系统(main inertial navigation systems, MINS)获取的参数包括姿态、速度及位置信息, 由于现有平台及子惯导之间的交互存在匹配上的限制, 一般采用速度匹配的对准方式。姿态信息能够对外界工况进行一定程度上的实时反映, 在随着平台的机动及姿态晃动过程中, 对准过程中的滤波器收敛速度及精度会随着外界工况受到影响。

文中针对动基座条件下, 对采用速度匹配方式的对准方法进行研究, 以期进一步缩短对准时间。通过对速度注入参数的特性辨识, 在线优化阵取值, 以加快滤波收敛速度; 同时, 充分利用主惯导能够获得的姿态信息, 对敏感到的俯仰、横滚等水平姿态角参数晃动特性进行辨识, 以此为基础, 对滑动窗口阈值进行实时自适应设定, 以在不同工况条件下, 第一时间进行调平判定, 形成一种基于主惯导参数特性分析的传递对准调平方法。

1 方法概述

如何缩短对准时间, 一般从两方面采取措施: 一是加快滤波器收敛速度。在滤波器收敛过程中, 在满足可观测性的条件下, 对于特定观测量而言, 量测噪声阵的取值对对应状态量的收敛速度及收敛误差起直接作用。一般情况下,阵依靠对观测量的辨识经验设定初始值后不再改变, 其无法适应于不同工况下存在的观测量差异, 在不同工况下有可能造成较大的收敛误差。采用阵自适应后, 其收敛精度依赖于阵估计精度。要保证收敛精度, 需要一定时间等待阵估计至一定精度, 这将导致滤波器收敛时间增加。二是提前判定调平的时间。现阶段的调平判据主要依靠经验设定固定调平时间, 该方法为了能确保滤波器在一定时间内完全收敛, 会设计充分的时间余量而造成时间浪费; 或者设定滑动窗口进行滤波器收敛判定, 该方法虽能较早觉察到滤波的收敛, 但其窗口阈值不变, 面对诸多工况间的差异时, 无法进行区别, 以致以一种判据进行判定并不是一种科学的做法[4-7]。

基于以上问题, 在原本速度匹配传递对准基础上, 充分利用主惯导获取的速度噪声特性及姿态晃动特性, 针对滤波器内部参数及调平判据进行如下设定。

1) 采用阵序贯自适应算法进行滤波估计, 初期设定较小的阵初始值强制加快滤波器的收敛速度, 并对注入参数进行在线实时监测辨识。随后, 根据获取的速度噪声特性, 进行阵自适应滤波, 在不失收敛速度的同时, 保证滤波器的平稳收敛。

2) 自适应设计调平判据, 即在线根据监测的水平角晃动特性, 采用神经网络预测失谐角收敛误差, 根据其误差值按照“由小及大”的原理实时变更相应的滑动窗口判定阈值, 进行调平判据判断, 一段时间的失谐角误差成功被“捕获”进窗口后, 进行调平判定。

1.1 模型建立

文中估计状态量采用11维参数, 且

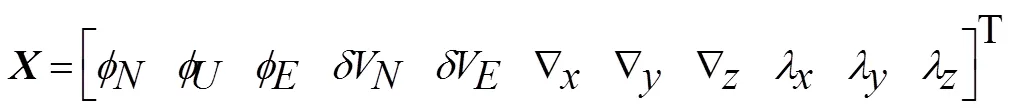
文中主要对北向失谐角及东向失谐角进行估计, 以修正初始姿态阵, 其中航向角信息采用直接注入方式。系统阵在此不作赘述。

对准方式采用速度匹配方式, 观测量采用北向速度及东向速度

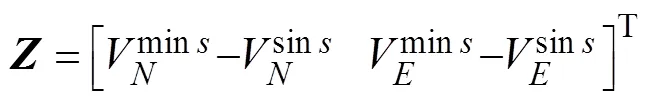
滤波器采用经典Kalman滤波, 且

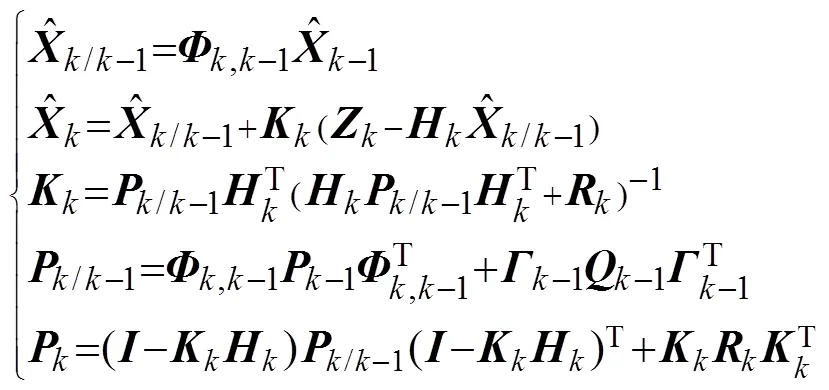
1.2 R阵序贯自适应算法

在速度匹配方式基础上, 为充分利用MINS注入参数特性, 加快滤波收敛速度, 缩短对准时间, 文中采用阵序贯自适应的方法进行滤波估计, 即, 在前期无法预知观测值噪声特性的情况下, 强制设计1个较小的阵初值(文中设定=0.1), 使得失谐角估计能尽快进行收敛, 在此阶段设计阵固定值估计时间为7.5 s(阵能够估计到一定精度)。7.5 s后, 根据监测的观测值噪声特性进行自适应滤波(此时阵初始值设定为较估计值大一些, 以适于阵随后的估计过程), 以在失谐角收敛阶段尽量平稳且接近真实值[8]。阵自适应算法参考

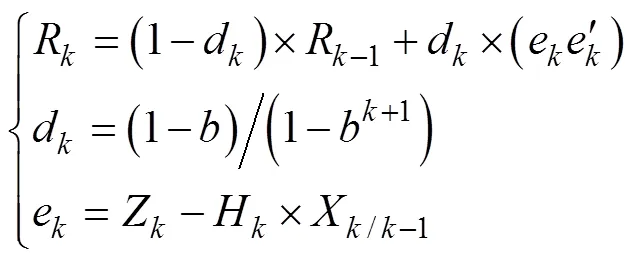
式中:e为观测量误差;为自适应因子(为了达到较好的自适应估计效果, 取0.96)。

以下对文中设计的阵序贯自适应算法与阵传统固定值算法及阵自适应算法进行仿真结果比较(如图1), 以北向失谐角收敛情况及北向速度观测噪声估计值为例(文中阵自适应初始值设为2)。

如图2所示, 从上述仿真结果可见, 序贯自适应方法, 无论是相比传统固定值方法, 还是纯自适应方法, 皆能满足快速收敛及后期平稳收敛至接近真实值的效果。在平台晃动的条件下, 仿真显示出同样的效果, 在此不再赘述。

1.3 神经网络预测滑动窗口阈值

综上所述, 平台机动及风浪或洋流干扰使得平台产生晃动, 在不同对准工况下, 失谐角收敛精度存在理论上的最高值, 因此单一的设定调平判据会造成不同工况下对准时间的差异及浪费, 甚至在恶劣工况下无法进行调平的情况。为保证不同工况下, 初始对准皆能快速进行调平判定, 以缩短对准时间, 调平判据应实时进行自适应设定, 其需建立在对外界工况的辨识基础之上。文中针对MINS传递水平姿态角(即俯仰、横滚方向)的晃动特性, 对滑动窗口阈值的自适应设定进行研究。

一般的, 平台晃动可以根据MINS传递水平姿态角用周期震荡形式表征

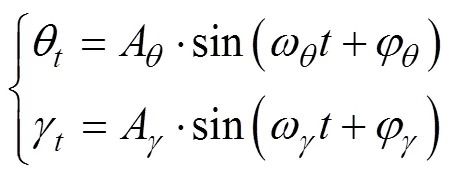
根据前期仿真结果, MINS传递水平姿态角参数特性中, 幅值及周期(即频率)对失谐角收敛段误差影响较大, 文中亦着重研究其与收敛段误差的关系, 并建立其与失谐角稳态误差之间的关系, 以作为滑动窗口阈值设定依据。图3为对随机2 000个不同周期、幅值得到的失谐角收敛段误差仿真做出的对应关系曲线图, 3维图对应关系为周期-幅值-北向失谐角收敛误差。

根据图3显示, 当幅值和频率同时增大时, 其北向失谐角收敛误差显示出随两变量增大的特性。为了建立上述四参量(俯仰、横滚的幅值及频率)与二参量(北、东向失谐角稳态误差)之间的复杂非线性关系, 同时保证输入输出之间映射的快速性, 文中考虑采用反向传播(back propagation, BP)神经网络进行复杂非线性拟合, 以隐含层作为“黑盒子”通过前期大量数据进行自适应训练, 快速映射出输出与输入之间的关系。图4为反向传播(back propagation, BP)神经网络非线性拟合算法流程, 包括建模、训练和预测。

在保证较短的训练时间基础上, 为提高网络精度, 通过资料所提出的经验公式, 及后期大量的试验验证, 确定网络设计为3个隐含层, 隐含层函数为logsig, 输出层函数为purelin。在 2 000组数中, 选取1 900组作为训练样本, 100组作为预测样本, 图5为预测样本与真实样本的比较[9-11]。

图6中可见, BP神经网络经自身训练后, 其预测输出误差大部分不超过0.0015º, 少数也不超过0.003º, 在动基座调平判定中, 该误差能够满足滑动窗口阈值设定精度需求。

参照上述数据库, 即可根据外界晃动情况, 进行初步的失谐角理论收敛精度的预估。依据该预估值, 结合指标要求, 即可根据外界环境自适应地设计滑动窗口阈值, 以适应不同工况下的快速调平。

2 仿真结果与分析

文中设计的仿真对比试验, 根据注入参数水平角变化特性设定滑动窗口阈值, 对序贯自适应方法与阵初始准确设定方法相比较, 仿真结果如下。

2.1 数学仿真

仿真条件: 陀螺常值漂移5º/h; 陀螺随机噪声5º/h; 加计常值零偏5×10–3g; 加计随机噪声5×10–3g; 注入的速度噪声0.2 m/s; 注入的水平角变化特性: 幅值正弦2º, 周期15 s。数据周期5 ms, Kalman滤波周期50 ms,阵贯序时间7.5 s, 自适应初始值2。仿真结果如图7所示。

在上述仿真中, 序贯自适应算法初期波动较大, 但能较快进行收敛; 结合晃动特性通过BP神经网络预测失谐角收敛段误差为0.036 829º、0.031 477º, 将其设定为调平判定滑动窗口阈值。阵序贯自适应算法于15.9 s完成调平判定, 准确固定阵设定算法于18.05 s完成调平判定。

2.2 半实物仿真

现场条件:利用自研惯性测量装置(inerti- alunit, IMU)及手动简易支架转台, 模拟现实情况下的对准工况, 采集产品实际数据输出, 对上述方法进行验证。经基准数据观测(见图8), 俯仰角晃动周期约为15 s, 幅值12º; 横滚角晃动周期为1.25 s, 幅值10.8º, 速度为0。数据采集周期为5 ms, Kalman滤波参数设定不变。

分别用阵准确固定值、阵自适应及文中所述方法进行对准, 结果见图9。

由图9可知, 半实物仿真结论与数学仿真相似。结合晃动特性预测北向、东向失谐角收敛段误差分别为0.184 4º、0.026 4º。阵序贯自适应算法于20.15 s完成调平判定, 准确固定阵设定算法于26.4 s完成调平判定。

实际过程中, 对准调平时间指标一般在30 s以上, 文中所述方法能够较迅速地完成收敛过程, 且能自适应进行调平判定, 在不同工况下较早地完成调平判定, 证明了该方法的有效性。

3 结束语

文中主要研究了在传递对准过程中, 除了引入MINS速度注入参数进行对准过程外, 同时考虑将速度噪声特性及水平角变化特性作为对准流程及调平判定的参考因素及依据。将MINS可获取的导航参数作为子惯导外的观测量进行考虑, 研究结果表明, 以速度噪声特性为依据, 对阵进行序贯自适应, 能够在一定程度上使阵估计至真实值附近, 加快滤波收敛速度, 平滑滤波收敛; 同时, 以水平姿态角变化(晃动)特性作为依据, 根据不同工况对调平判定滑动窗口阈值进行设计, 在不同工况下, 能够较早开始进行调平判定, 射前缩短对准时间, 以实现鱼雷的快速准备。

在晃动条件下, 滤波器稳态段也会呈现出波动特性, 采用滑动窗口的方式进行调平, 无法确定调平时刻在波动曲线的准确位置, 需对在波动曲线的不同位置调平对对准精度的影响进行分析。因此, 未来需进一步精确调平时刻的设定。

[1] 骆斐, 尤太华, 刘运鹏, 等.扰动基座下捷联惯组初始对准[J].战术导弹技术, 2016(6): 76-79.Luo Fei, You Tai-hua, Liu Yun-peng.et al.Initial Alignment of SIMU with Disturbances[J].Tactical Missile Te- chnology, 2016(6): 76-79.

[2] 郜福全, 陈丽容, 丁传红, 等.UD分解自适应滤波在SINS初始对准中的应用[J].计算机工程与设计, 2017, 35(1): 158-162.Gao Fu-quan, Chen Li-rong, Ding Chuan-hong.et al.Initial Alignment of SINS Based on UD Factorized Adaptive Filter[J].Computer Egnineering and Design, 2017, 35(1): 158-162.

[3] 苏宛新.自适应UKF滤波在SINS初始对准中的应用[J].中国惯性技术学报, 2011, 19(5): 533-536.Su Wan-xin.Application of Adaptive UKF Filter Technique in Initial Alignment of SINS[J].Journal of Chinese Inertial Technology, 2011, 19(5): 533-536.

[4] 刘红光, 张崇猛, 陈伟, 等.舰艇干扰因素对速度匹配传递对准性能的影响[J].中国舰船研究, 2013, 8(4): 86-91.Liu Hong-guang, Zhang Chong-meng, Chen Wei, et al.In- terference Factors of Velocity Matching and Transfer Al- ignment for Shipboard Weapons[J].Chinese Journal of Ship Research, 2013, 8(4): 86-91.

[5] Chen Y, Zhao Y.New Rapid Transfer Alignment Methodfor SINS of Airbome Weapon Systems[J].Journal of Sy- stems Engineering and Electrics, 2014, 25(2): 281-287.

[6] Fairfax L D, Fresconi F E.Position Estimation for Projectiles Using Low-cost Sensors and Flight Dynamics[J].Journal of Aerospace Engineering, 2014, 27(3): 611-620.

[7] 王艳永, 杨功流, 王永苗, 等.捷联惯性导航系统动态传递对准性能综合评估[J].中国惯性技术学报, 2013, 21(4): 425-429.Wang Yan-yong, Yang Gong-liu, Wang Yong-miao, et al.Comprehensive Assessment for Dynamic Transfer Align­m- ent Accuracy of Strap-down Inertial Navigation System[J].Journal of Chinese Inertial Technology, 2013, 21(4): 425- 429.

[8] 苌永娜, 张海, 李玉洁, 等.基于R阵动态估计的自适应滤波算法[J].电光与控制, 2012, 19(6): 26-31.Chang Yong-na, Zhang Hai, Li Yu-jie, et al.An Adaptive Kalman Filtering Algorithm Based on the Dynamic Estimation of Measurement Noises[J].Electronics Optics & Control, 2012, 19(6): 26-31.

[9] 章毅, 郭泉, 王建勇.大数据分析的神经网络方法[J].工程科学与技术, 2017, 49(1): 9-18.Zhang Yi, Guo Quan, Wang jian-yong.Big Data Analysis Using Neural Network[J].Advanced Engineering Scien­ces, 2017, 49(1): 9-18.

[10] Silver D, Huang A, Maddison C J, et al.Mastering the Ga- me of Go with Deep Neural Networks and Tree Search[J].Nature, 2016, 529(7587): 484-489.

[11] Wang J, Wu W, Zurada J M.Deterministic Convergence of Conjugate Gradient Method for Feedforward Neural Net- works[J].Neurocomputering, 2011, 74(14-15): 2368-2376.

Transfer Alignment and Leveling Method Based on Characteristics of MINS Parameters

YANG Guan-jin-ziLI Jian-chenHUANG HaiGUO Lin-na

(The 705 Research Institute, China Shipbuilding Industry Corporation, Xi’an 710075, China)

The initial alignment time directly relates to the fast prefiring performance of a torpedo.The internal parameters of traditional alignment algorithm and leveling criterion are fixed, which results in longer alignment time and poor adaptation to different alignment conditions.To solve the problem, this study proposed an alignment and leveling method based on the characteristics of main inertial navigation system(MINS) speed injection parameters and horizontal attitude angle sloshing parameter.The back propagation(BP) neural network was used to identify these characteristics, and the internal specific parameters were online adaptively updated in real time.Hence, on the premise of guaranteeing the alignment accuracy, fast convergence rate of the filter and timely leveling judgment in different working conditions could be ensured.Comparative test shows that the proposed method can effectively accelerate the convergence rate of the detuning angle, adaptively design the leveling criterion according to different working conditions, and shorten the initial alignment time.

torpedo; main inertial navigation system(MINS) parameters; transfer alignment; leveling judgment; back propagation(BP) neural network

TJ630.33; U675.7

A

2096-3920(2018)06-0537-06

10.11993/j.issn.2096-3920.2018.06.005

2018-03-15;

2018-07-25.

杨管金子(1988-), 男, 在读博士, 工程师, 主要研究方向为水下无人系统制导技术.

杨管金子, 李建辰, 黄海, 等.基于主惯导参数特性的传递对准调平方法[J].水下无人系统学报, 2018, 26(6): 537-542.

(责任编辑: 杨力军)