基于元启发算法的纯方位被动定位方法

赵伟康, 韩一娜, 杨益新, 刘清宇



基于元启发算法的纯方位被动定位方法

赵伟康1, 韩一娜1, 杨益新1, 刘清宇2

(1.西北工业大学 航海学院, 陕西 西安, 710072; 2.海军研究院, 北京, 100073)

传统的最小二乘的纯方位被动定位方法虽然运算简单, 但是定位结果不够可靠。基于此, 文中探究了利用元启发算法进行纯方位被动定位的可能性, 构建了相应的数学模型, 给出了具体的算法。通过对比该方法与传统方法的效果, 同时对该方法在水声观测环境下的应用进行仿真, 得出该方法的定位效果相较传统的最小二乘定位方法有显著的优势。

纯方位被动定位; 元启发算法; 最小二乘法

0 引言

目前, 国内外应用元启发算法进行无线定位优化的研究主要集中在无线传感器网络(wireless sensor network, WSN)定位中, 文献[1]通过改进差分进化算法以适用于WSN定位问题; 文献[2]利用差分进化算法改进距离无关(range-free)定位中典型的DV-Hop算法; 文献[3]使用粒子群算法进行WSN定位; 此外还有很多利用优化算法进行定位优化的研究[4-6]。以上的研究主要针对的是WSN中的自定位, 待定位对象是在网络中活动的节点, 不涉及目标的定位。基于此, 文中提出将元启发算法应用于非合作目标的纯方位被动定位, 以取代传统的基于最小二乘的定位方法[7-8]。目标定位问题本质上是基于观测数据的点估计, 在多传感器联合观测的环境下, 目标定位实际上是信息融合的过程[9-10], 在适当的建模后元启发算法能够很好地完成目标统计信息的融合, 给出可信的定位结果。

1 纯方位被动定位问题及传统解法

1.1 纯方位被动定位问题

纯方位被动定位问题指的是观测区域分布着若干传感器(在水声环境下指的是水声换能器基阵), 这些传感器被动工作且只能返回目标的方位估计(direction of arrival, DOA), 同时, 传感器的性能指标(即测量方差)、坐标以及参考方向(对于水声基阵即是基阵的朝向)均是已知的。

如图1所示, 纯方位被动定位问题即是要试图在已知4个传感器位置、传感器测量误差模型以及4个测量出来的方位的情况下估计出目标的位置。对于纯方位被动定位问题二维空间最少需要2个传感器才能完成定位, 这时候的定位方法是交叉定位, 当具有更多的传感器时可以用它们提供的信息修正定位结果。

1.2 基于最小二乘的纯方位定位方法

图1中4个传感器的观测形成了由4条射线组成的射线簇, 这些射线两两相交。最小二乘法试图在图中找出关于4条射线距离的平方和最小的点, 可以证明这个点就是4条射线形成的不规则四边形的重心, 该重心总是能用解析的形式表达出来。在文献[3]中有详细的三维条件下最小二乘交会被动定位方法的推导。这种方法的优点是其结果是解析的, 将观测结果代入相应公式即可得到定位结果。但是其间忽略了2个问题: 首先是在多个传感器性能差距比较明显的时候, 该方法并没有办法区分它们, 性能差的传感器携带了更少的目标信息, 却能无差别和性能优的传感器一起影响定位结果; 其次是某个点到观测射线的距离并不能完整地表征该点成为目标的可能性, 接近某个传感器的点距离观测射线的距离必然很短, 但是这并不能保证其成为目标的概率很大。因此, 需要寻找到一种可以考虑到这2个问题的模型。

2 基于元启发算法的纯方位被动定位

2.1 元启发算法概述

元启发算法(meta-heuristic algorithm)是区别于精确算法(exact algorithm)的一类算法, 它能向一些复杂的优化问题提供近似最优解, 尤其是应用于非凸的优化问题。文中使用的元启发算法为差分进化(differential evolution, DE)算法[11], 具有原理简单、易于实现、全局寻优能力较好和鲁棒性强等特点, 因此在科学研究和工程应用领域都得到了广泛应用。DE算法与其他类似功能的元启发算法的区别在于其关注了变量之间的相关性, 比较契合文中的优化情景。

2.2 数学模型

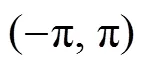
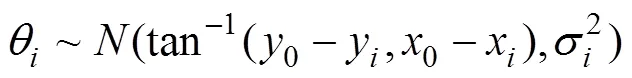
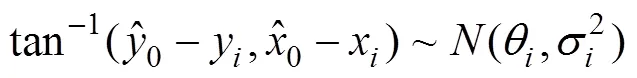
式(2)构建了目标关于传感器的真实方位在已知观测方位后的后验分布, 为了构建以目标真实位置为参数的似然函数, 还需要额外假设传感器的有效测量距离为。

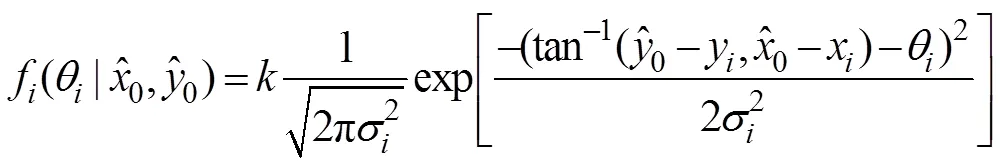
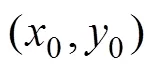
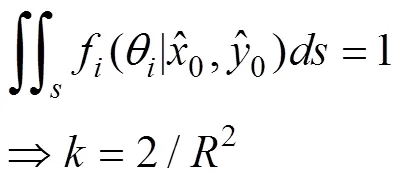
半径存在的意义在于如果不约束传感器测量的距离, 式(3)无法成为一个概率密度。对每个传感器的的要求是, 其圆形观测区域应该能包括目标的活动区域。

该概率密度在空间中的特点是射线上的概率密度相同, 其直观表现如图2所示。

图2中目标真实位置在(1000, 2000)处, 传感器位于原点。为了后续的计算方便, 对概率密度取负对数, 深红色区域表示概率密度大。

当多个传感器作用于该区域时, 由于它们之间的观测是相互独立的, 因此整个区域中某个点的概率密度正比于它在每个传感器上的概率密度的乘积, 即

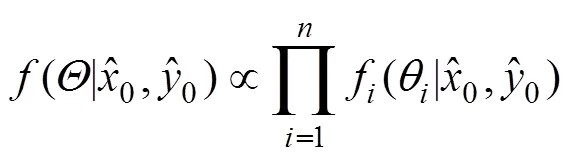
将式(5)带入式(3), 则在每个传感器的有效测量范围相同时, 有式(6)所示联合似然函数, 可以成为估计目标位置的依据。

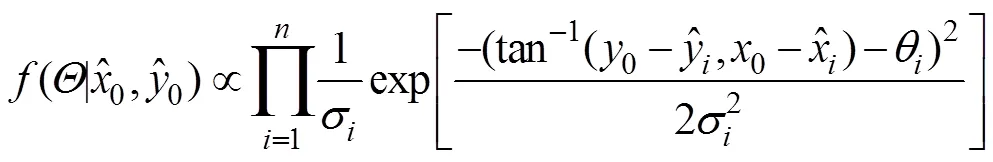
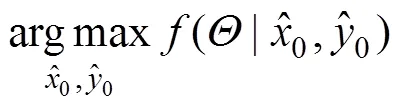
式(7)的目标函数十分复杂, 它依赖于包括观测集和传感器性能的诸多变量, 最优化问题最常见的对目标函数偏导数求极值的方法并不适用, 因为该方法数学形式不仅极其复杂且涉及到超越方程的求解, 即该最优化问题是找不到解析解的。另一个方法是网格搜索, 该方法较笨重, 无法同时满足高搜索精度和低运算量的要求。对于这类最优化问题, 元启发算法提供了一个新的思路。

2.3 差分进化算法求解模型

常见的元启发算法大多能在一定程度上解决非凸优化问题。式(7)的目标函数在图3的情景中是一个凸函数, 但在更为不规律的传感器布局下, 无法保证其始终是凸函数, 该函数局部最优值的数量是可控的, 它受限于传感器的规模。因此, 选择使用差分进化算法来求解式(7)中的优化问题, 它的差分算子和变异算子为算法提供了跳出局部最优解而寻求全局最优解的能力。

图4表示差分进化算法的普遍流程。该优化问题的目标函数只有2个变量, 因此算法压力并不大, 可以很快向全局最优解收敛。差分进化算法在该问题中泛用性很强, 而且在观测环境发生变化(传感器位置漂移、传感器发生更换和增减、观测的背景噪声变化等情况)时, 仅需要维护差分进化算法的适应度函数(对于优化问题即指优化函数本身)。

3 算法仿真分析

仿真分析分为两部分, 第1部分比较在相同的观测条件下文中方法和最小二乘法的性能; 第2部分是模拟该方法在分布式的水声监测网络中的工作情况。

第1部分仿真对不同的传感器测量标准差和不同的目标位置使用2种方法进行定位运算。使用100次蒙特卡罗试验的均方根误差大小来衡量定位结果的优劣

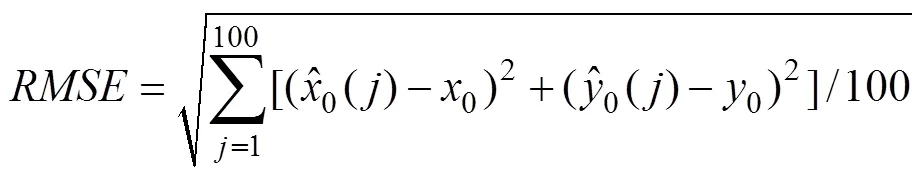
式(8)在统计意义上表达了定位的结果与真实位置的直线距离, 该值越小表示定位越准确。表1为不同条件下2种算法的性能对比, 其中用LS代指最小二乘的方法, 用ML-DE代指文中提出的方法。

表1中每一个情况都是有代表性的, 它们分别是: 1) 传感器性能好, 传感器误差相同, 目标在观测区域中央; 2) 传感器性能较差, 传感器误差相同, 目标在观测区域中央; 3) 传感器性能较好, 传感器误差有差异, 目标在观测区域中央; 4) 传感器性能好, 传感器误差相同, 目标偏离观测区域中央; 5) 传感器性能较差, 传感器误差不同, 目标偏离观测区域中央。根据结果可以看出,仅在各个传感器性能相同且目标与各传感器距离相同时, 最小二乘方法的效果才能接近文中方法。在传感器性能存在差异和目标真实位置距离传感器存在差异时, 最小二乘方法的效果明显降低, 这是其数学模型中没有考虑传感器性能差异和目标与传感器距离导致的, 理论上在该方法中一个性能极差的传感器能够平等的和其他传感器一起干预定位结果, 这违背了信息融合的原则。

表1 不同条件下2种算法的性能对比

第2部分仿真主要模拟该算法在水声应用背景下的定位效果。在水声环境下被动测向的精度受到很多因素影响, 例如信噪比、阵列布局、目标真实方位(端射方向的误差明显小于边射方向)、阵元间时延测量的误差, 以及DOA算法的选取都会影响对目标的观测模型。文中仿真考虑一种分布式的水声监测网络, 空间中存在大量独立工作的传感器节点, 每个传感器节点仅有2个接收单元, 采用相位法测向, 即通过测量2个水听器接收信号的相位差来解算目标方位。这样的传感器节点单独工作测向精度是不理想的, 无法达到阵元多孔径大、搭载了更为复杂的DOA算法的水声基阵的性能, 但是可以用多传感器信息融合的收益来提高精度。

图5体现了文中算法在水声监测网络的效果。图中分布有1个岸基节点和8个海上节点, 岸基节点测向精度较高, 方位估计偏差标准差为0.5º。海上节点标准差为2º。同时, 海上节点还存在自定位误差, 协方差为diag([100,100])。使用文中方法对(2000, 2000) m处的目标定位, 结果为(2062, 2055) m。

为了比较不同算法对该环境的定位误差, 选择主流的2种定位方法: 一种为正交向量估计器(orthogonal vectors, OV)的最小二乘方法和总体最小二乘方法(total least-squares, TLS)[12]。同样使用均方根误差衡量定位精度, 改变海上节点的测向标准差, 以上3种方法在不同测向精度下的表现如图6所示。

图6显示了3种算法对位置(6000 m, 6000 m)和(10000 m,10000 m)目标的定位效果。这2个位置分别代表了距离节点分布区域较近和较远的情况。在目标距离传感器节点较近时, 文中方法较其他2种方法的优势明显, 而其他2种方法效果相当。在目标距离传感器节点较远时, 3种方法的定位效果都有明显下降, 这是纯方位测量的固有特性, 此时文中方法依旧优于其他2种方法。

4 结束语

提出了一种应用于多传感器被动定位的方法, 主要针对传感器分布不固定, 传感器之间性能差距较大的情景, 该方法的定位效果相对于传统的最小二乘定位方法有显著的优势。同时, 模拟了该方法在水声环境下的应用, 在配合水声被动探测惯用的方法时, 可获得可靠的定位效果。

[1] 杨俊.差分进化算法的改进及在无线传感器网络定位问题中的应用[D].西安: 西安电子科技大学, 2015.

[2] 杨楚皙.基于差分进化的DV-Hop定位改进算法[D].吉林: 吉林大学, 2015.

[3] Li H, Xiong S W, Liu Y, et al.A Localization Algorithm in Wireless Sensor Networks Based on PSO[J].Computer Science, 2011, 6729: 200-206.

[4] Kannan A A, Mao G, Vucetic B.Simulated Anneaing Based Location in Wireless Sensor Network[C]//Proceedings of the 30th Annual IEEE Conference on Local Computer Net- works(LCN).Sydney: IEEE, 2005: 513-514.

[5] 叶蓉, 赵灵锴.基于蚁群粒子群混合的无线传感器网络定位算法[J].计算机测量与控制, 2011, 19(3): 732-735.Ye Rong, Zhao Ling-kai.Localization Algorithm for Wireless Sensor Network Bosed on ACOPSO[J].Com­pu­ter Measurement & Control, 2011, 19(3): 732-735.

[6] 孙美玲.基于遗传算法的无线传感器网络节点自定位算法研究[D].青岛: 中国石油大学, 2009.

[7] 谭维茜.多站纯方位被动跟踪粒子滤波算法研究[D].南京: 南京理工大学, 2009.

[8] 样柏胜.被动多传感器探测目标跟踪技术研究[D].西安: 西安电子科技大学, 2009.

[9] Stefano Coraluppi.Multistatic Sonar Localization[J].IEEE Journal of Oceanic Engineering, 2006, 31(4): 964-974.

[10] Mahler R P S.多源多目标统计信息融合[M].范红旗,卢大威, 刘本源, 等译.北京: 国防工业出版社, 2013.

[11] Storn R, Price K.Differential Evolution-A Simple and Efficient Heuristic for Global Optimization over Conti­nuous Sp- ace[J].Journal of Global Optimization, 1997, 11(4): 341-359.

[12] Kutluyil Dogancay.Bearings-only Target Localization Using Total Least Squares[J].Signal Processing, 2005, 85(9): 1695-1710.

Bearing-Only Passive Location Based on Meta-Heuristic Algorithm

ZHAO Wei-kang1, HAN Yi-na1, YANG Yi-xin1, LIU Qing-yu2

(1.School of Marine and Technology, Northwestern Polytechnical University, Xi’an 710072, China; 2.Naval Research Academy, Beijing 100073, China)

Because the traditional bearings-only passive location approach based on the least square method cannot give much reliable location result, this paper explores the possibility of solving bearing-only passive location problem via the meta-heuristic algorithm, builds a corresponding mathematical model, and deduces a specific algorithm.Moreover, application of this method in underwater acoustic observation environment is simulated, and compared with traditional method.The result indicates that this method can achieve much better localization effect, compared with the traditional least square based passive location method.

bearings-only passive location; meta-heuristic algorithm; least square method

O229; TP301.6

A

2096-3920(2018)06-0623-05

10.11993/j.issn.2096-3920.2018.06.018

2016-11-19;

2016-12-18.

国家重点研发计划(2016YFC1400200); 国家自然科学基金面上项目(61671388).

赵伟康(1995-), 男, 硕士, 主要研究方向为融合跟踪算法。

赵伟康,韩一娜,杨益新,等.基于元启发算法的纯方位被动定位方法[J].水下无人系统学报, 2018, 26(6): 623-627.

(责任编辑: 陈 曦)