基于最小二乘的被动声呐浮标多普勒最接近算法

张立琛, 张 驰, 张晓亮



基于最小二乘的被动声呐浮标多普勒最接近算法

张立琛1,2, 张 驰1,2, 张晓亮1,2

(1.中国船舶工业系统工程研究院, 北京, 100094; 2.水声对抗技术重点试验室, 北京, 100094)

为提高被动声呐浮标参数估计精度, 提出一种基于最小二乘的多普勒最接近算法。算法在新多普勒最接近算法基础上, 利用目标辐射噪声中特征频率的多普勒信息, 构建一个长方矩阵, 在最小二乘意义下, 计算目标最接近距离和速度。使用泰勒展开公式, 分析了算法的误差特性。计算机仿真及空气试验表明, 该算法可以正确计算出目标参数。与被动声呐浮标其他算法相比, 显著地提高了目标参数估计精度。

被动声呐浮标; 最小二乘; 多普勒最接近算法; 目标参数估计

0 引言

被动声呐浮标是浮标系列中重要的一种, 其参数估计的基本算法之一是多普勒最接近(Dop- pler-CPA, DC)算法。DC算法通过测量并记录目标多普勒数据来计算目标的速度和最接近点(closest point of approach, CPA)距离(即当目标运动到离被动声呐最接近时的距离)[1-2]。DC算法从理论上讲仅是一个近似公式, 只能计算出目标径向速度和近似的最接近距离。当距离较大时, 该算法计算误差很大。文献[3]在DC算法的基础上提出了一种新算法, 该算法推出了一个无误差的计算公式, 即accurate DC(以下简称ADC), 具有重要的理论意义。同时, 此算法在实际使用中更为方便, 它不需要求取CPA点频率变化的1阶导数, 而且输入数据没有必须关于CPA点对称的限制[3]。

文章在文献[3]的基础上提出了基于最小二乘多普勒最接近算法(least square DC, LSDC)。该算法使用多个目标多普勒数据, 在最小二乘意义下解算目标参数。由于利用多点数据, 预期可提高计算精度。同时设计进行了计算机仿真和空气环境模拟试验, 以验证该算法的正确性与有效性。

1 ADC算法

根据多普勒频移公式, 浮标检测到目标的线谱频率为[4]

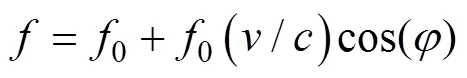
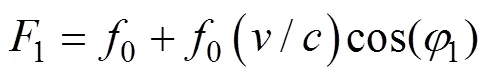
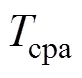
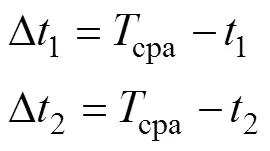
由式(1)可知

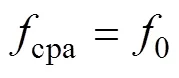
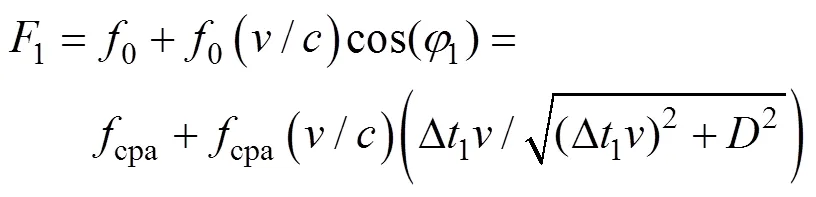
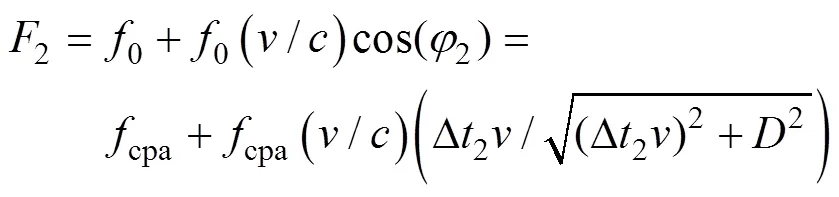
对式(6)和式(7)两边平方、化简, 并记

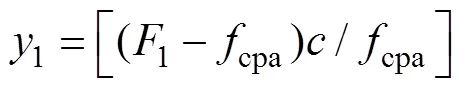
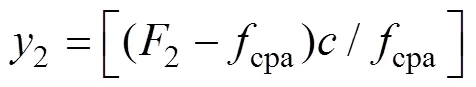
则有

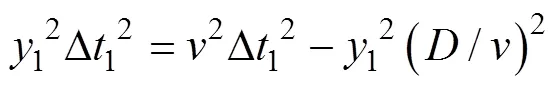
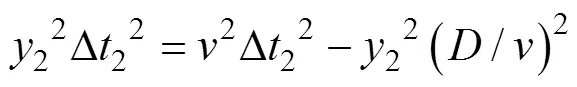
用矩阵形式可以表示为

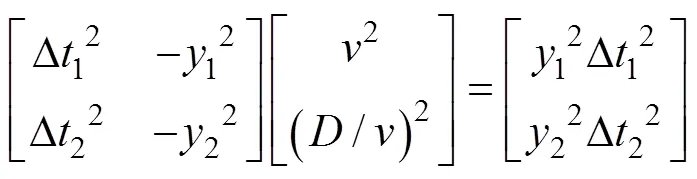
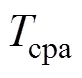
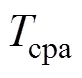
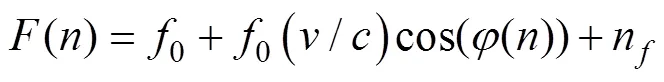
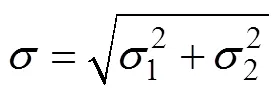
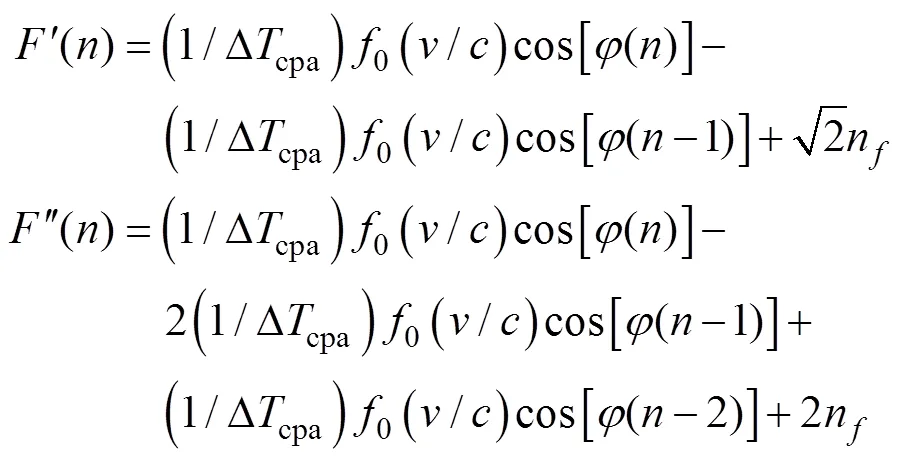
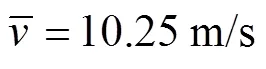
2 LSDC算法

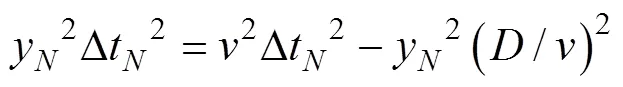
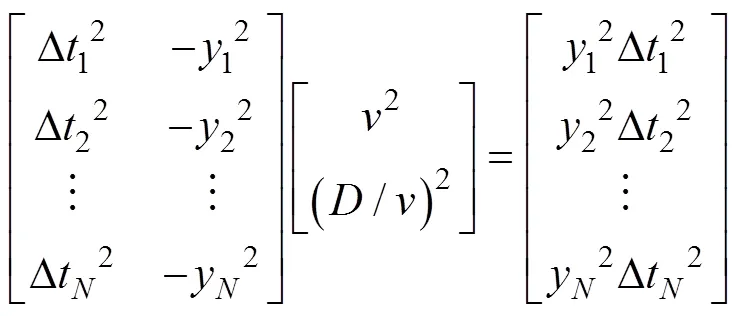
记作

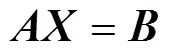
其中

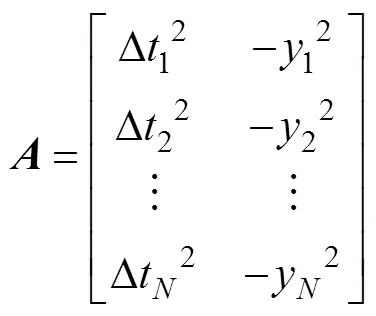
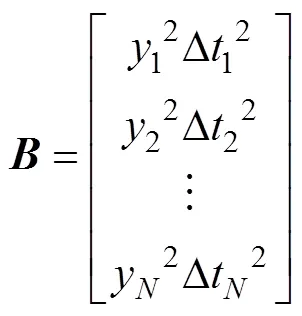
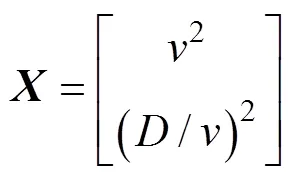
在最小二乘意义下, 可以获得方程的解

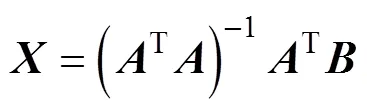
通过上式可计算出目标的CPA点距离和速度。

该算法利用了目标多个多普勒信息, 利用最小二乘原理, 可以获得最小二乘意义下的最佳解, 其精度优于ADC算法。

3 算法误差分析

在LSDC及ADC算法中, 计算目标经过CPA点的时刻及此时刻的目标特征频率是整个算法的第1步, 也是后续计算的基础, 因此这2个参数的估计精度将直接影响所有后续结果的精度[5]。

首先讨论CPA点时刻的误差, 如图2所示。为了计算简单, 假定目标过CPA点的时刻为0时刻。

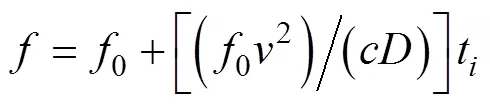
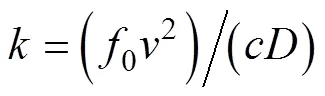
时间可表示为

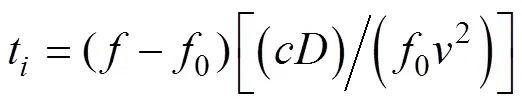
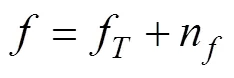
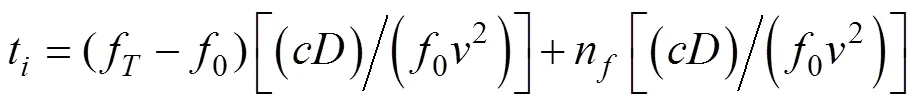
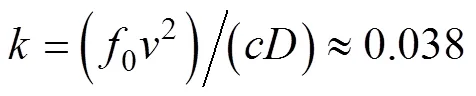
为了解决此问题, 在计算时先对记录的多普勒数据进行低通滤波, 尽量消除噪声影响, 以提高计算精度, 满足实际使用的精度要求。由于多普勒变化是一个慢变过程, 低通滤波器的截止频率可以设计得很低。

4 计算机仿真

对每种距离进行LSDC算法仿真并重复500次, 统计结果见表1。表中的均值是500次仿真结果的统计平均值, 反映算法是否能收敛到真值上; 均方差是500次结果的统计方差, 反映算法的一致性。

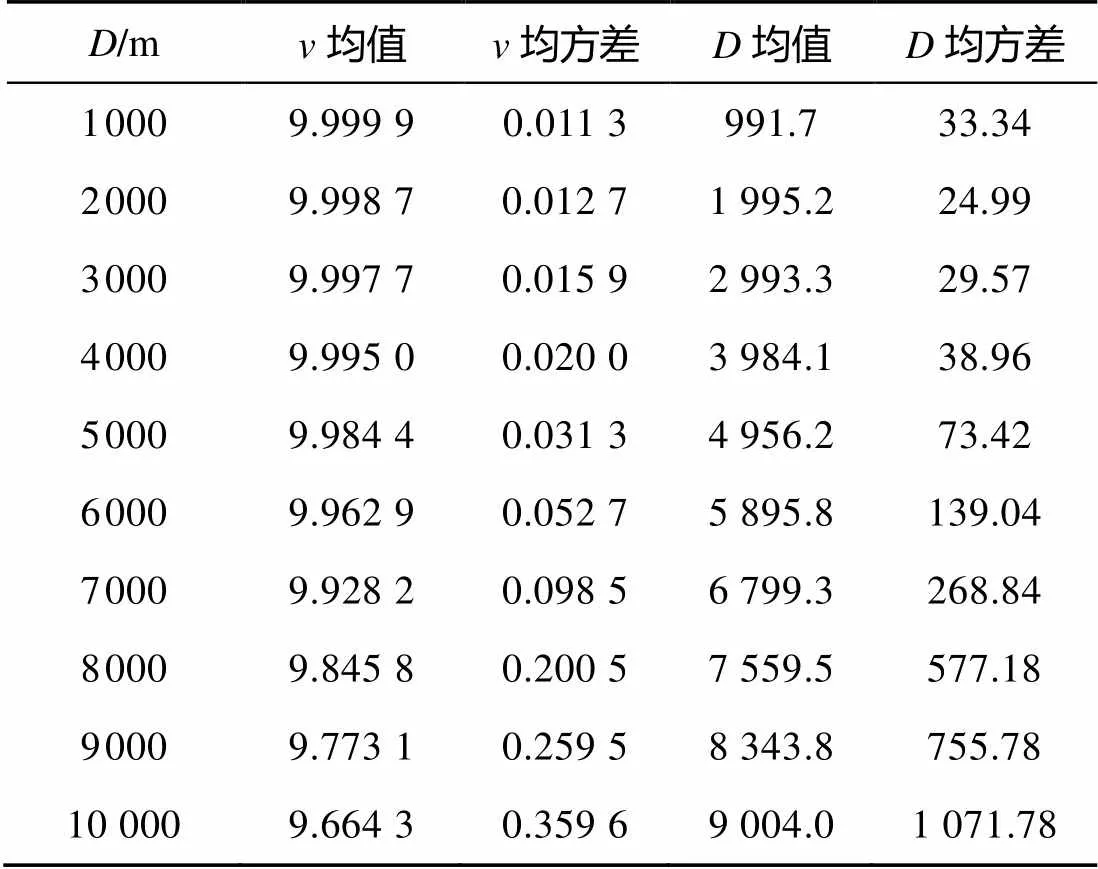
表1 基于最小二乘多普勒最接近算法仿真结果

从表1可看出, LSDC算法对目标速度的估计相当精确, 在测频噪声0.1 Hz, 距离10000 m的情况下, 速度估计误差仅有0.359 6 m/s。

对距离的估计误差随着CPA点距离的增加而增加, 与第3章误差分析结果一致。在10 000 m时, 测量的距离相对误差为10%。考虑到被动声呐浮标只进行频率测量, 同时附加0.1 Hz的频率测量噪声, 这样的误差仍是可以接受的。

使用DC算法在相同仿真条件=1000 m,=10 m/s下进行仿真, LSDC速度计算精度提高了2500倍, 统计均方差缩小20倍; 距离计算精度提高74倍, 统计均方差缩小41倍。

5 试验原理及处理算法

5.1 试验原理

考虑到在水下进行高速目标运动试验的难度, 选择在空气中进行算法验证试验。空气声速是水中声速的0.2266倍, 多普勒频移相应增加, 对目标参数估计有利。不利的因素是空气中更容易受到各种外界干扰, 同时声音传播损失增加, 严重降低信号信噪比。

试验地点选择在一条平直的公路上, 利用汽车来模拟水下高速运动目标。试验设备分为信号发生和采集两部分。信号发生部分利用汽车为载体, 使用信号发生器产生1个单频信号, 经过功率放大, 推动大功率扬声器发声, 来模拟水下目标的单一特征线谱。信号采集部分由高灵敏度麦克风、滤波放大器、频谱分析仪、数据采集仪及示波器组成。麦克风拾取空气中的环境噪声及目标特征频率, 经过滤波、放大, 最终由数据采集仪采集并存储。频谱分析仪和示波器作为监视设备分别从时域和频域对噪声信号进行观察。

试验时(如图4所示), 汽车以恒定速度行驶在公路上, 模拟水下目标运动, 匀速通过麦克风, 即CPA点。信号采集部分采集环境噪声和目标线谱, 并由数据采集仪存储。

试验内容主要是通过改变不同的目标线谱频率、CPA点距离(图4中)及车速, 利用采集数据计算和, 验证算法的正确性及不同因素对算法带来的影响。

5.2 处理算法

采集的噪声谱线是带噪声的连续信号, 为了精确估计每个时刻的频率, 采用短时傅里叶变换算法来估计频率, 每次FFT变换长度256个采样点, FFT重叠率50%, FFT算法长度1024。获得每个时间段的FFT后, 选择幅度最大的频率点作为此时刻段的频率测量值。

对计算后的频率信号进行平滑滤波, 使用32阶FIR低通滤波器, 低通截止频率100 Hz。

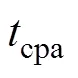
5.3 试验结果及分析

试验过程中, 麦克风灵敏度–45 dB, 麦克风频率响应50 Hz~18 kHz; 放大器增益60dB; 滤波器通带频率范围为0~20000 Hz; 数据采集仪采样频率5000Hz。试验选取了4种不同的CPA点距离, 分别为7 m, 11.6 m, 15 m和20 m(由于实际公路环境的限制, 最大距离20 m)。车速选取4种速度, 即20 km/h, 40 km/h, 60 km/h和80 km/h。信号频率分别为600 Hz, 1000 Hz和2000 Hz 3种。数据处理时空气中声音传播速度取=340 m/s。下面给出几个典型的处理结果。

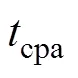
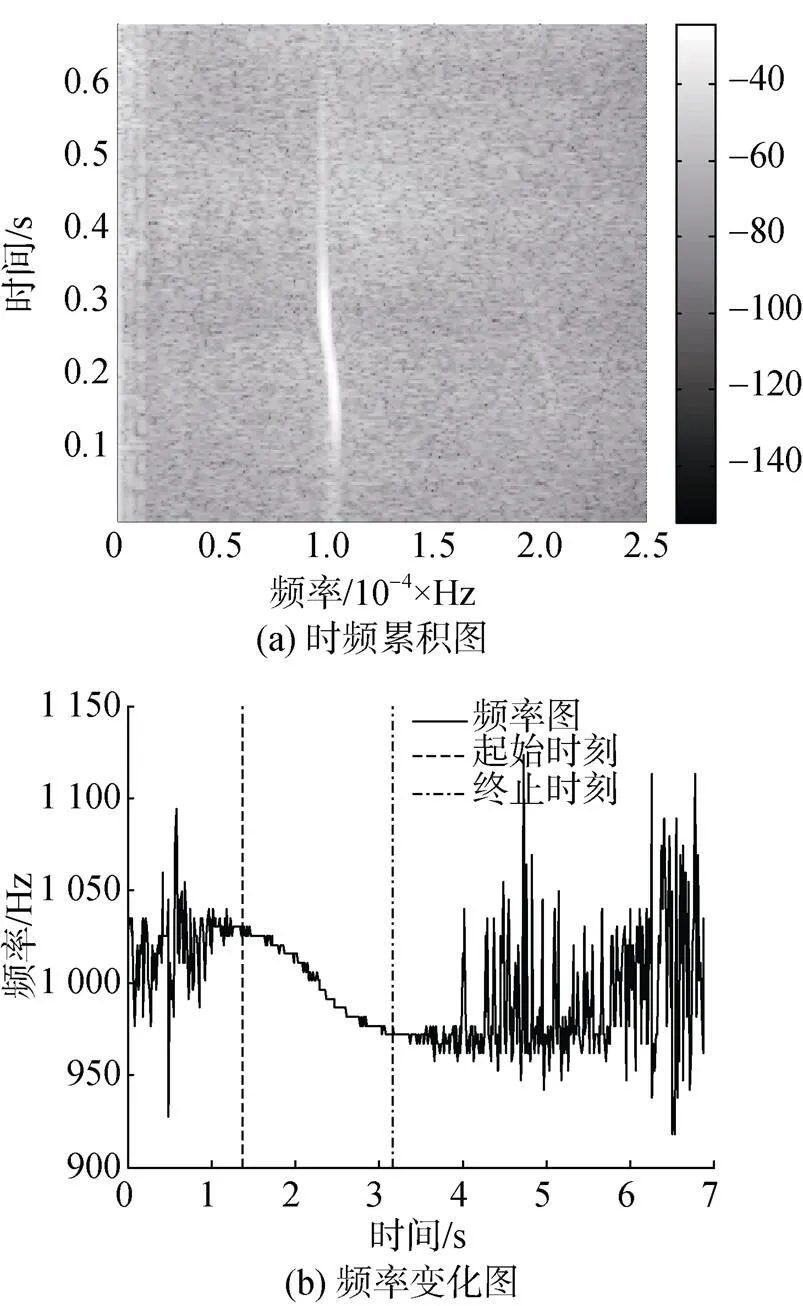
图5 距离7 m, 速度40 km/h, 特征频率1 000 Hz时的试验数据分析结果

图6为CPA距离最远时, 距离20 m, 速度40 km/h, 特征频率1 000 Hz的处理结果。参与计算的数据长度为6.3 s。计算结果距离16.74 m, 速度35.79 km/h。可以看出, 随着距离的增加, 目标线谱变化率减小, 根据式(22)可知, 计算误差将增加。与第3节误差分析结果一致。

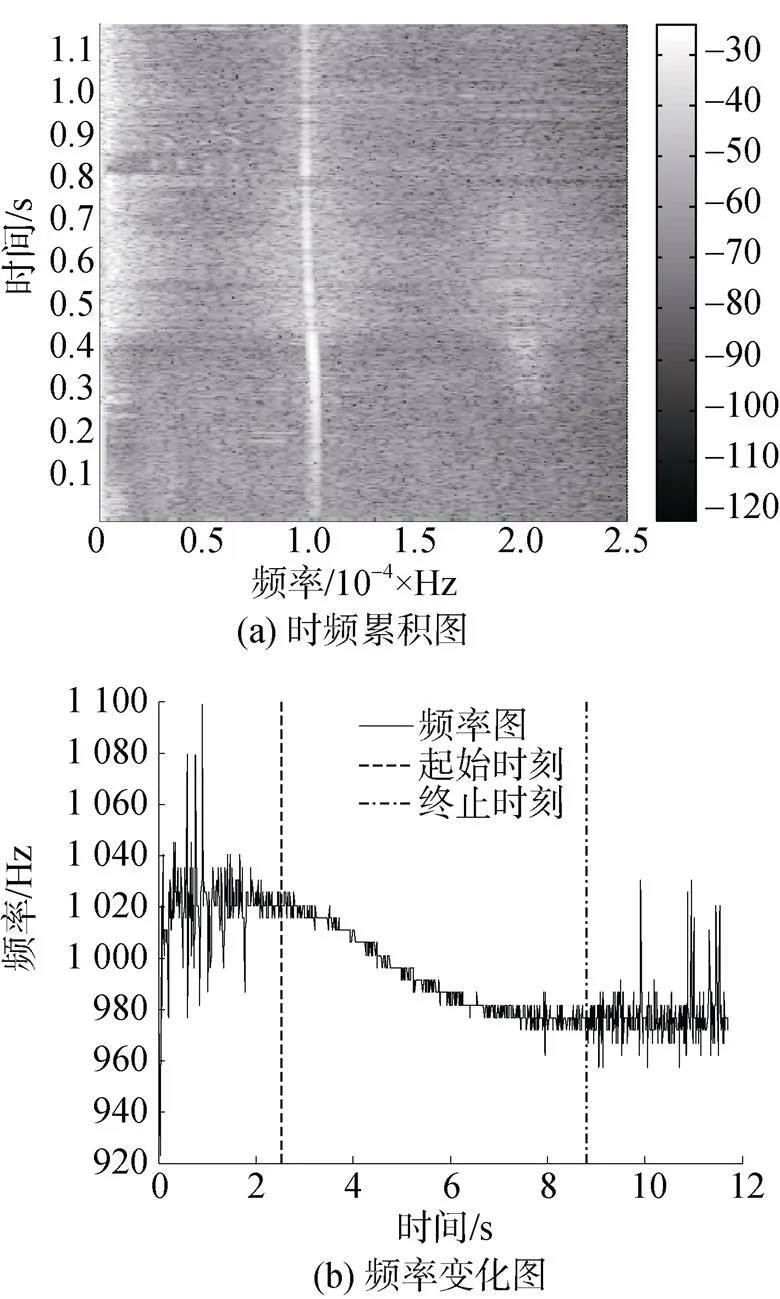
图6 距离20 m, 速度40 km/h, 特征频率1 000 Hz时的试验数据分析结果

整个试验过程共计20次有效过程, 经过后期分析处理, 结果如表2所示。

从表2数据可以看出, 试验取得了较好的结果, 大部分过程可以很好地估计出目标运动参数, 距离估计误差小于10%的约为60%, 速度估计误差小于10%的约为70%。

表1和表2的结果表明, 目标速度计算精度要优于最接近距离的计算精度。根据式(20), 目标速度可以直接解算得到。而目标最接近距离解算需要代入解算的目标速度, 因此会增加计算误差。

由于试验公路有来往车辆通过, 给某些试验过程带来干扰。其中有3个试验过程中不同程度受到公路其他宽带噪声的干扰, 分别为第3、5、10号过程。如10号, 距离11.6 m, 速度40 km/h, 特征频率1000Hz, 试验中, 正好有重型卡车慢速驶过, 带来一个宽带连续噪声, 如图7(a)所示。宽带噪声干扰使CPA点的频率出现大的跳变, 如图7(b)所示, 导致计算的目标参数误差较大。计算目标距离8 m, 速度34 km/h。

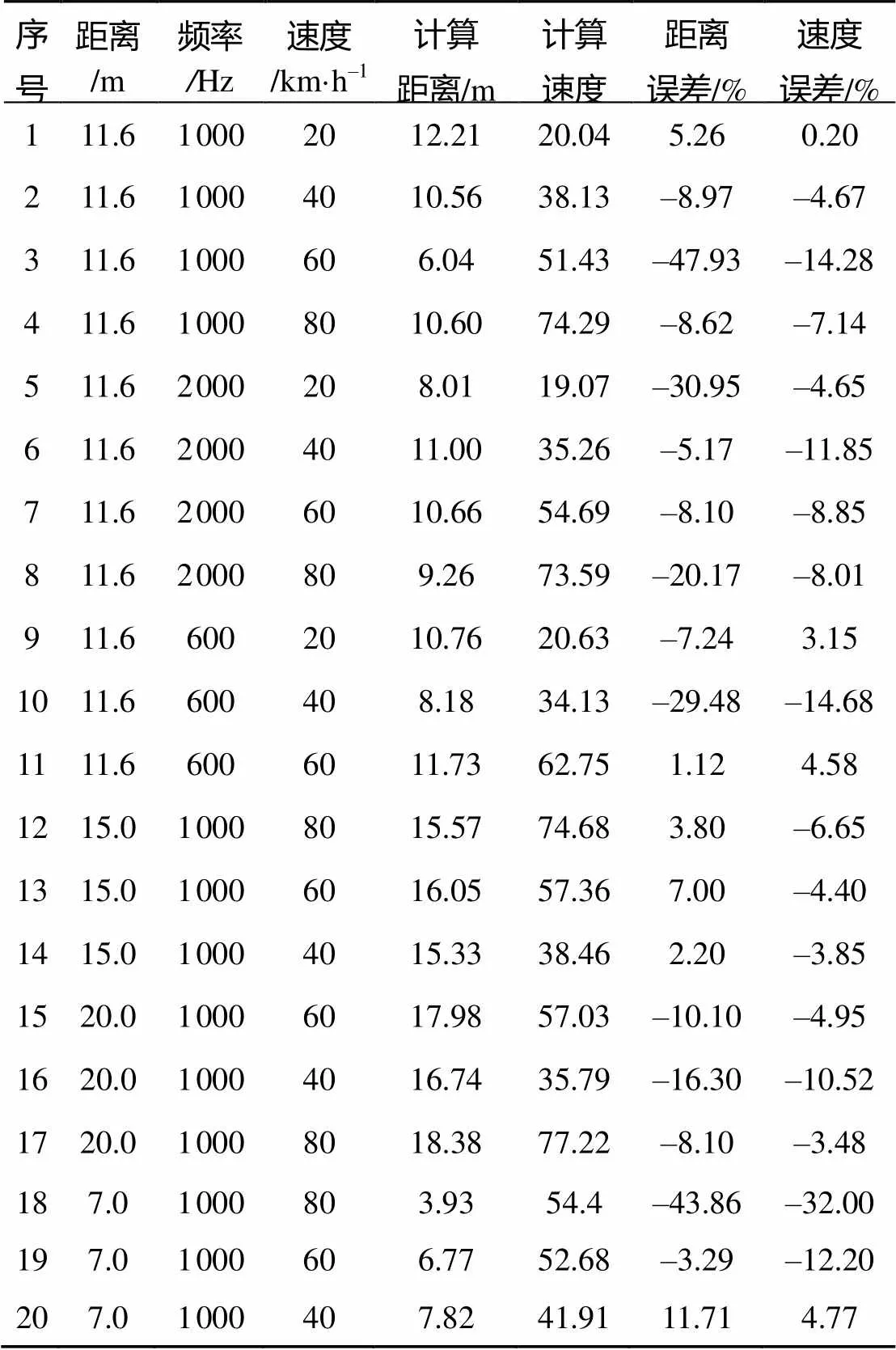
表2 试验结果

可见, 处理结果的好坏与采集信号的质量有很大关系。此外, 8号、18号过程车速为80 km/h, 由于空气中声音传播损失较大, 加上车速很高, 采集到的有用数据很少, 导致处理误差很大。

6 结束语

在DC算法的基础上, 利用最小二乘原理, 提出了新的LSDC算法, 该算法仅仅被动收听目标的辐射噪声, 利用噪声中特征线谱的多普勒信息, 求解出目标在最小二乘意义下的绝对运动速度和CPA点距离。

计算机仿真验证了此算法的正确性。在20次试验过程中, 3个过程受到干扰, 其余17个过程中, 计算距离误差小于10%的约为70%, 计算速度误差小于10%的约为82%。计算误差大于10%的过程主要是因为外部干扰, 或参与计算的有效数据太少导致。总的来看, 试验结果取得了很好的结果, 验证了该算法的正确性和有效性, 计算结果误差分布与理论分析一致。在仅仅被动采集目标特征线谱条件下, 计算出目标的绝对速度和CPA点距离, 表明了算法具有实际使用价值。

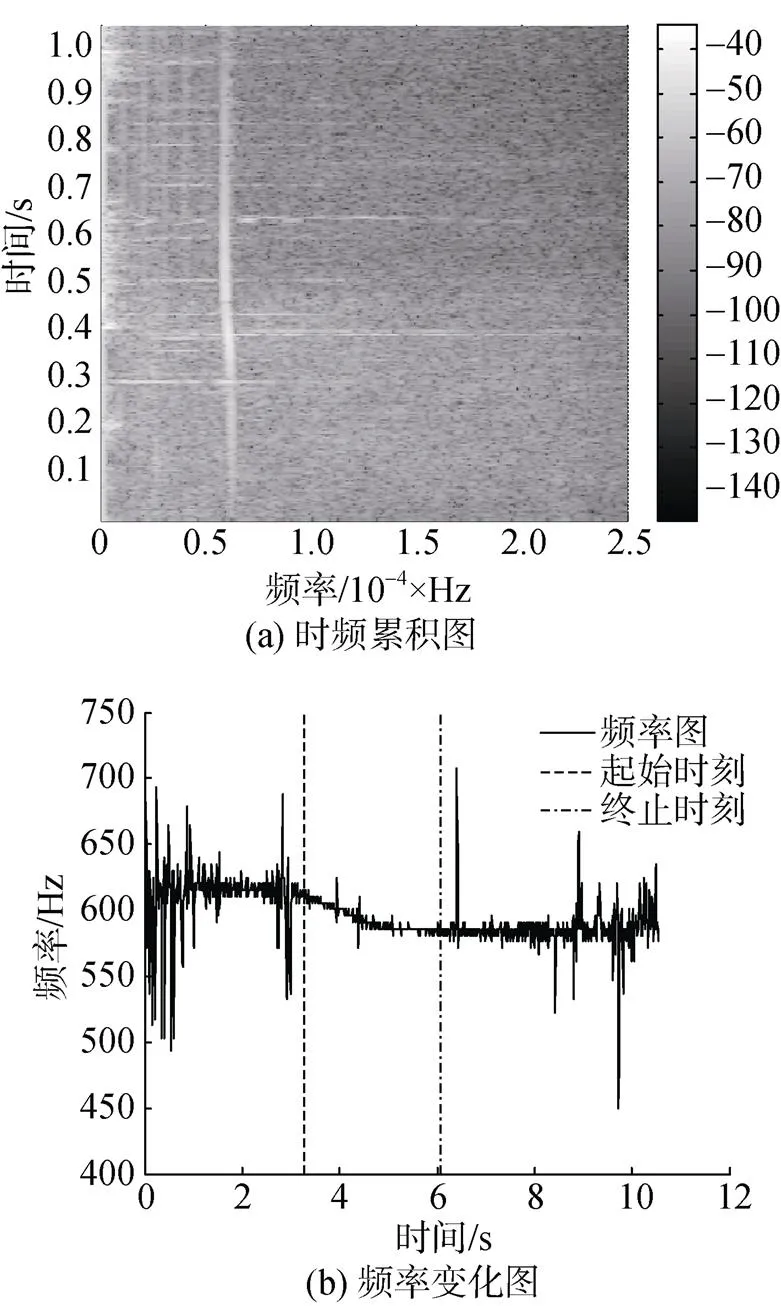
图7 有宽带噪声干扰下的试验数据分析结果

通过以上研究, 提出下一步的研究方向可能有: 在实际海洋环境验证算法的正确性和有效性; 在目标经过CPA点之前完成对目标的参数估计; 由于目标可能存在多个特征频率, 充分利用这一特征, 进一步提高计算精度; 多个被动声呐联合解算目标参数等。

[1] 蓉竹.机载声呐浮标和吊放声呐[J].现代军事, 2006(1): 62-63.

[2] 张晓利, 陈建勇.吊放声呐与声呐浮标在应召搜潜中的联合运用[J].海军航空工程学院学报, 2006, 21(6): 669- 671.Zhang Xiao-li, Chen Jian-yong.Joint Application of Dip­ping Sonar and Sonobuoy in Answering the Call to Anti- Submarine[J].Journal of Naval Aeronautical Engineering Institute, 2006, 21(6): 669-671.

[3] 陶林伟, 王英民, 王成, 等.声纳浮标多普勒最接近法的一种新算法[J].系统仿真学报, 2008, 20(23): 6353- 6355.Tao Lin-wei, Wang Ying-min, Wang Cheng, et al.New Algorithm for Sonobuoy Doppler-CPA[J].Journal of System Simulation, 2008, 20(23): 6353-6355.

[4] 田坦, 刘国枝, 孙大军.声呐技术[M].哈尔滨: 哈尔滨工程大学出版社, 1999: 21-24.

[5] 陶林伟, 王英民.一种新的单枚被动定向浮标目标定位算法[J].兵工学报, 2011, 32(3): 365-369.Tao Lin-wei, Wang Ying-min.A Target Location Algo­rithm Based on Single Direction Finding and Ranging Sonobuoy[J].Acta Armamentarii, 2011, 32(3): 365-369.

[6] Tao Lin-wei, Wang Ying-min.Target Localization Based on Joint Measurement of Amplitude and Frequency in a LOFAR Field[J].Journal of Zhejiang University-Science A, 2014, 15(2), 130-137.

[7] 刘俊星, 章新华, 綦敦浩, 等.单水听器被动测距的脉冲周期最接近法[J].应用声学, 2013, 32(1): 10-14.Liu Jun-xing, Zhang Xin-hua, Qi Dun-hao, et al.Pulse Periods Closest Point of Single Hydrophone Passive Ranging[J].Applied Acoustics, 2013, 32(1): 10-14.

[8] 刘俊星, 章新华, 綦敦浩, 等.基于脉冲周期的单元被动测距[J].电声技术, 2012, 36 (12): 46-48.Liu Jun-xing, Zhang Xin-hua, Qi Dun-hao, et al.Single Unit Passive Ranging Based on Pulse Periods[J].Audio Engineering, 2012, 36(12): 46-48.

[9] 刘俊星, 章新华, 綦敦浩, 等.单水听器被动测距的信赖域最优化算法[J].兵工学报, 2012, 33(9): 1118-1123.Liu Jun-xing, Zhang Xin-hua, Qi Dun-hao, et al.Trust Region Optimization Method for Single Hydrophone Passive Ranging[J].Acta Armamentarii, 2012, 33(9): 1118-1123.

[10] 郁涛.对水下目标的多普勒直接定位[J].中国电子科学研究院学报, 2011, 6(3): 328-330.Yu Tao.Doppler Direct Location for Underwater Target[J].Journal of China Acadewy of Electronics and Information Technology, 2011, 6(3): 328-330.

Doppler Closest Point of Approach for Passive Sonobuoy Based on Least Square

ZHANG Li-chen, ZHANG Chi, ZHANG Xiao-liang

(1.Systems Engineering Research Institute, Beijing 100094, China; 2.Science and Technology on Underwater Acoustic Antagonizing Laboratory, Beijing 100094, China)

To improve estimation precision of the passive sonobuoy parameters, a least square based Doppler closest point of approach (CPA) is proposed.On the basis of the new Doppler CPA, Doppler information of the characteristic frequency in radiated noise of target is used to construct a rectangular matrix, and the least square principle is employed to obtain the least square solutions to the nearest distance and speed of a target.Then, the error of the algorithm is analyzed using Taylor expansion formula.Computer simulation and air experiments show that the proposed method can calculate the target parameters correctly, and compared with other algorithms of a passive sonobuoy, the precision of target parameter estimation is improved significantly.

passive sonobuoy; least square; Doppler CPA; target parameter estimation

TJ630.34; TB566

A

2096-3920(2018)06-0605-07

10.11993/j.issn.2096-3920.2018.06.015

2018-08-01;

2018-11-22.

国家重点研发计划项目资助(2016YFC1400206).

张立琛(1986-), 男, 博士, 工程师, 主要研究方向为水声和水声对抗技术.

张立琛,张驰,张晓亮.基于最小二乘的被动声呐浮标多普勒最接近算法[J].水下无人系统学报,2018,26(6):605-611.

(责任编辑: 陈 曦)