电驱动海洋绞车主动升沉补偿自抗扰控制系统

廖 薇 赵延明 刘德顺,3 金永平，3

1.湖南科技大学机电工程学院，湘潭，411201 2.湖南科技大学信息与电气工程学院，湘潭，411201 3.湖南科技大学海洋矿产资源探采装备与安全技术国家地方联合工程实验室，湘潭，411201

0 引言

海洋绞车是水面支持系统中关键的甲板机械装备，广泛应用于水下拖曳系统、海底深水硬件安装、海洋钻探、海洋管道铺设、深海石油和天然气开发等海洋资源勘探与深海作业环境中[1]。由于经常在深海海洋动荡不定的场合下工作，受风浪、潮涌的作用，母船会出现上下起伏的现象，母船受风浪影响上下起伏不仅会对收放缆绳产生巨大的作用力，从而导致其断裂(尤其是脐带缆容易受到破坏)，而且作用力会通过缆绳传递到起重物，引起重物的摇荡。海洋绞车的卷筒应该具有升沉补偿功能，当拖船与被拖物之间的缆绳张力由于风浪等因素发生变化时，卷筒会自动收放缆绳，把重物的位移波动控制在一定的范围内，避免不均衡张力造成缆绳的损害以及对海底作业的影响。所以，在海洋绞车上配备主动升沉补偿装置可以大大增强海上作业的安全性、高效性和可靠性。

李海[2]在张力控制系统中使用模糊自适应PID控制器，把模糊参数通过自整定后放入常规PID控制器中，使系统响应速度快、容易控制；王生海[3]采用变参数PID控制方法，开展了垂直方向主动式波浪补偿控制系统的设计研究，达到了更好地波浪补偿的目的；王志刚[4]构建了一种基于模糊-PI控制的绞车恒张力系统，该控制系统具有良好的稳定性，可保证多台绞车在复杂海洋环境中的协同作业。

在重物收放过程中会受到海浪的外界扰动，海况是多变的，所以模型输入是随机变化的；而且电驱动海洋绞车升沉补偿控制系统是非线性的时变系统，其模型参数会随重物下放深度、下放速度、重物质量等的变化而发生变化，即其模型在重物收放过程中是变化的。以上方法虽然都有一定的控制效果，但是这些控制方法对模型的依赖性都较强，在海况和模型变化的情况下不能对其进行有效控制，还存在一定的缺陷。

自抗扰控制(active disturbance rejection control, ADRC)技术是由韩京清[5-7]在非线性PID的基础上提出的，它在强干扰和系统模型不确定时对系统仍有较好的控制效果。自抗扰控制器算法简单、易于实现、精度高、速度快、抗扰能力强，既可以处理确定系统的控制问题，又可以处理不确定系统的控制问题，还能抑制不需外扰模型的扰动等[6]，所以将自抗扰控制器应用到电驱动海洋绞车的升沉补偿中，能够有效提高绞车控制品质，具有重要的研究意义。

为了提高主动升沉补偿控制鲁棒性与响应速度，本文采用自抗扰控制器作为电驱动海洋绞车的升沉补偿控制器对电驱动海洋绞车系统进行动力学分析，建立电驱动海洋绞车系统数学模型和主动升沉补偿自抗扰控制系统的仿真模型并进行仿真分析。

1 电驱动海洋绞车系统动力学分析

电驱动海洋绞车系统主要由滚筒、收放架、滑轮、重物(重物为所吊负载)等组成，其结构简图见图1。

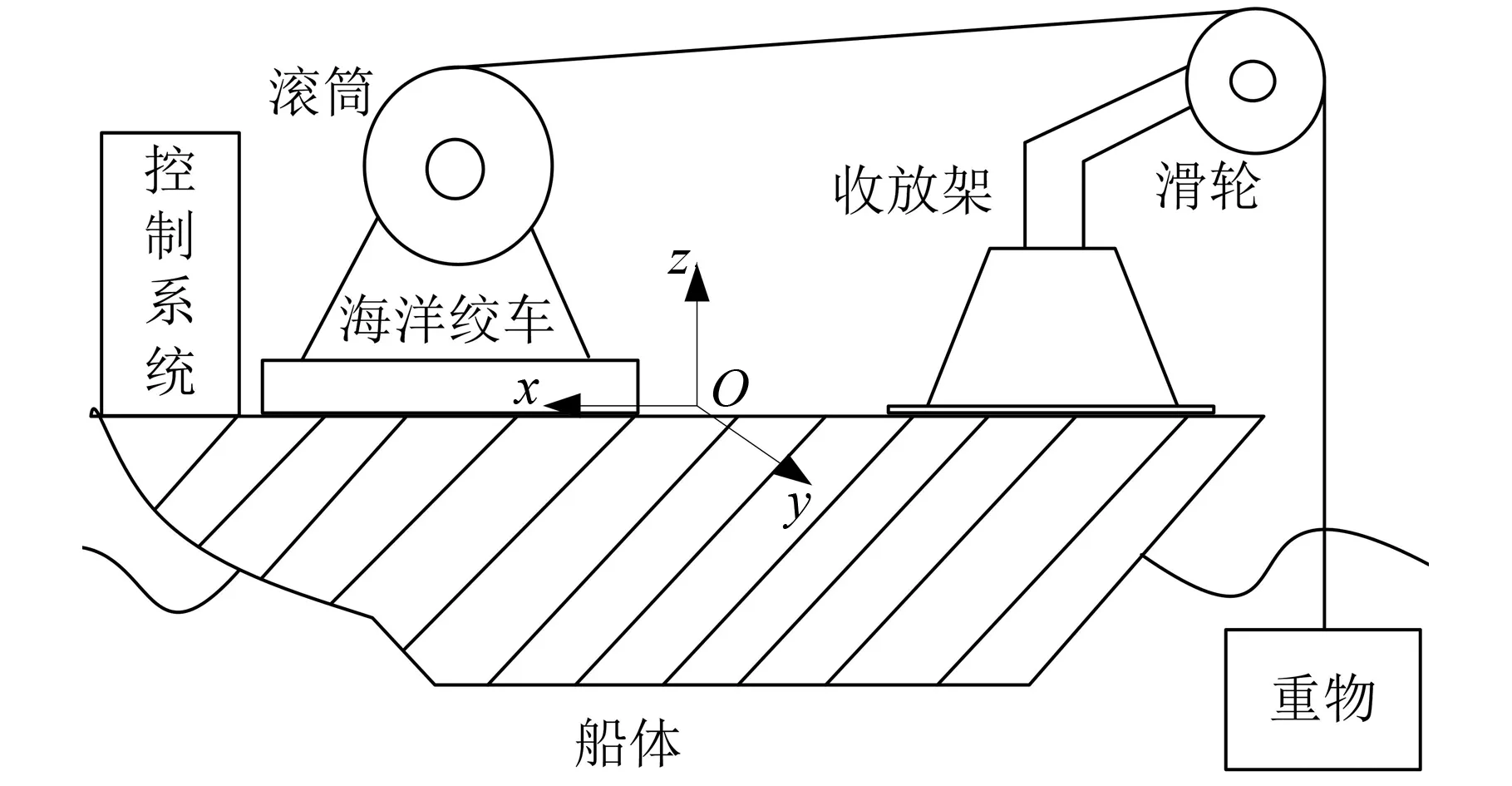
图1 电驱动海洋绞车系统结构简图Fig.1 The structural diagram of electric driven marine winch system

1.1 母船运动方程

本文采用基于动力学特征的简化模型，即将母船的运动看作垂直方向上的升沉，母船的升沉运动是由波浪运动引起的，它的运动规律可以看作简谐运动，其升沉位移由波高及船体的类型、结构、尺寸等因素决定。假设海浪是简单的正弦波，其波高为H，周期为T，升沉位移与波高比值为μ，则母船的运动方程近似为[8]

(1)

式中，z0为母船升沉位移。

将式(1)对时间t求一阶和二阶导，可以得到母船的升沉速度v0和升沉加速度a0：

(2)

(3)

1.2 波浪运动方程

流场速度势简化函数为[9]

(4)

k=2π/Lσ=2π/T

式中，k为波数；L为波长；d为水深；σ为波浪角频率。

将上式对z求偏导并忽略水平方向x的影响，可以得到水中任一水质点的垂直速度vw：

(5)

将上式对时间t求偏导，得到垂直方向上的水分子加速度aw：

(6)

1.3 重物运动方程

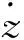
(7)

(8)

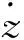
(9)

(10)

完全入水后，可忽略波浪运动的影响，重物的运动方程可由式(7)和式(8)表示。

1.4 缆绳张力计算

在重物入水之前，重物没有与海水接触，所以没有受到海水浮力与波浪力的作用，此时重物的运动可以表示为

(11)

式中，m为重物质量；FT为缆绳的张力。

将式(8)代入式(11)，可得重物入水前缆绳的张力：

(12)

重物刚入水后的一段时间内，重物受到海水浮力和波浪力的作用，此时重物的运动可以表示为[10]

(13)

式中，Fb为重物所受浮力；Fw为重物垂直方向上所受波浪力。

重物所受垂直方向的波浪力

(14)

式中，CL为阻力系数(一般取1.67)；ρ为海水密度；SL为重物在垂直方向上的受力面积。

将式(9)、式(10)和式(14)代入式(13)可以得到重物刚入水后一段时间缆绳的张力：

(15)

式中，V为重物排开海水体积。

当重物完全入水后，由于只有海洋表面的波浪较大，故重物完全入水后受到的波浪力可以忽略不计，且重物受到海水浮力，此时重物的运动可以表示为

(16)

将式(8)代入式(16)可得重物完全入水后缆绳的张力：

(17)

综上所述，由式(12)、式(15)和式(17)可以看出，无论入水前还是入水后，由于波浪和母船运动的作用，缆绳张力的动态响应均为振荡形式，缆绳的张力会随着重物的下放不断变化，缆绳时而拉伸时而收缩，这会使缆绳产生疲劳破坏，韧性下降，严重时会使缆绳达到疲劳强度而最终断裂，而且绞车缆绳一般为脐带缆，当缆绳张力较大时，缆绳会在一定程度上有所拉长，缆绳的收缩和拉伸会导致重物也随之上升或下降，所以应该对电驱动海洋绞车系统进行升沉补偿，在一定程度上抑制缆绳的疲劳损伤。

2 电驱动海洋绞车系统建模与分析

本文以某电驱动海洋绞车为研究对象，根据其系统的结构特点，可构建系统框图(图2)。本文采用输入-输出模型进行描述，将电驱动海洋绞车系统视为一个动态系统，以母船升沉速度作为输入，重物位移作为输出，通过观察重物位移的响应变化研究自抗扰控制器的控制效果。该控制系统框图的各模块如下。

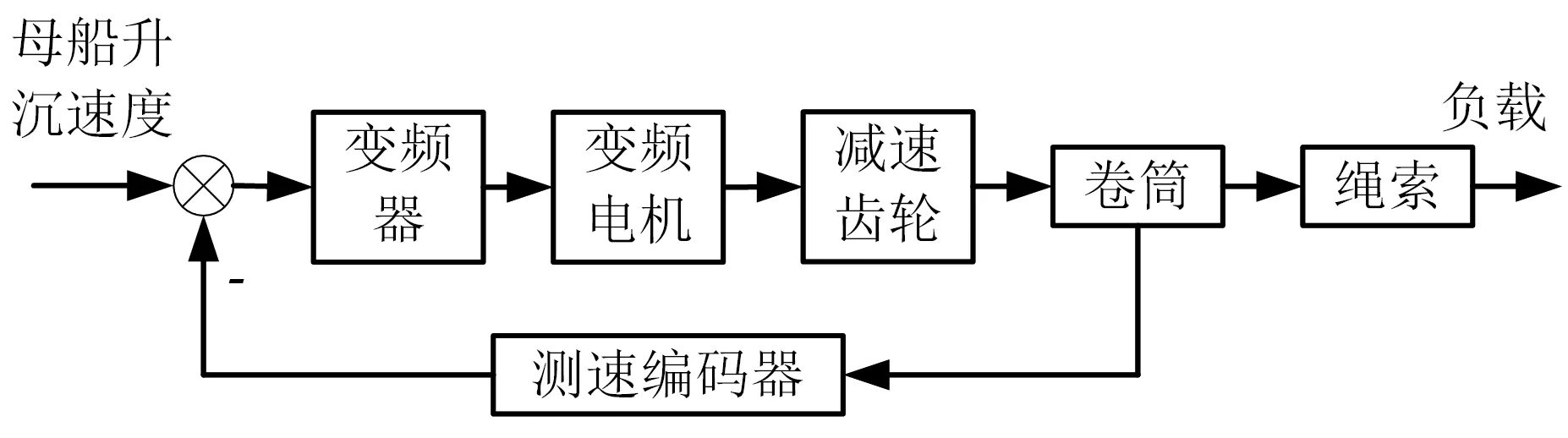
图2 电驱动海洋绞车系统框图Fig.2 The block diagram of electric drive marine winch system

2.1 变频电机-卷筒的数学模型

变频电机到卷筒的传递函数[11]为

(18)

mg=m+m1+m′m1=ρAlA=π(dc/2)2

式中，θ为卷筒转角；U1为变频电机输入电压；p为电机极对数；S′为转差率；R1为定子绕组的相电阻；R2为转子绕组的相电阻；N为线圈匝数；Kw为绕组系数；Φm为每极磁通量；X1为定子每相绕组的漏电抗；X2为转子每相绕组的漏电抗；J为传动部分折算到电动机轴上的总转动惯量；r为某时刻缆绳与滚筒总半径；i为齿轮传动比；mg为某时刻等效重物质量；m1为下放缆绳质量；A为缆绳横截面积；l为下放缆绳长度；m′为其他附加质量；dc为缆绳直径。

传动部分折算到电动机轴上的总转动惯量J可由下式计算：

J=mJrJ2=GD2/(4g)=Jd+J1+J2+J3+Js

(19)

式中，mJ为系统传动部分质量；rJ为系统传动部分半径；G为系统传动部分重力；D为系统传动部分直径；Jd为电动机转动惯量；J1为小齿轮转动惯量；J2为大齿轮转动惯量；J3为滚筒转动惯量；Js为缆绳转动惯量。

缆绳转动惯量Js由下式计算：

(20)

D4=D3+qdcm2=ρAlsls=qle

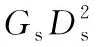
将式(20)代入式(19)可得

(21)

式中，GdD2d为电机飞轮矩；G1为小齿轮质量；D1为小齿轮直径；G2为大齿轮质量；D2为大齿轮直径；G3为卷筒质量。

2.2 卷筒到重物的数学模型

卷筒到重物传递函数[11]为

(22)

式中，R为卷筒半径；C为海水阻尼系数；A1为负载有效面积；Cd为阻尼系数(一般取0.5～0.6)；K为缆绳弹性刚度系数；E为缆绳弹性模量。

其他模块的数学模型都用比例系数的形式表示，KV为速度电压转换系数，K1、K2分别为变频器和变频电机的比例系数，Kf为测速编码器比例系数。

由式(21)可以看出，在重物下放过程中，绕在滚筒上的缆绳会随着重物下放而减少，则缆绳的层数q会减少，即绕滚筒的缆绳质量m2和缆绳与滚筒的总直径D4会减小，转动惯量J就会减小，这时变频电机到卷筒的传递函数也会发生变化，所以电驱动海洋绞车系统是一个非线性时变系统。

由式(18)、式(21)和式(22)可以看出，当下放缆绳长度l增加而其他参数不变时，缆绳弹性刚度系数K减小；下放缆绳质量m1增大，则等效重物质量mg增大；绕滚筒的缆绳质量m2减小，则传动部分总转动惯量J也会减小。当缆绳直径dc增加而其他参数不变时，缆绳横截面积A增大，则缆绳弹性刚度系数K增大,下放缆绳质量m1随之增大，则等效重物质量mg增大；同时D4也会增大，则总转动惯量J增大。当重物质量m增大而其他参数不变时，等效重物质量mg增大。所以下放缆绳长度l和缆绳直径dc的变化会引起等效重物质量mg、缆绳弹性刚度系数K和传动部分总转动惯量J的变化，而重物质量m的变化会引起等效重物质量mg的变化。

综上所述，可用各模块传递函数构建电驱动绞车系统的数学模型，并用MATLAB/Simulink的封装功能将电驱动海洋绞车系统进行封装，创建为子系统，作为电驱动海洋绞车主动升沉补偿系统的被控对象(命名为winch)，见图3。

图3 电驱动海洋绞车系统Simulink封装图Fig.3 The Simulink package of electric driven marine winch system

3 主动升沉补偿自抗扰控制系统建模

3.1 二阶自抗扰控制器的设计

自抗扰控制方法在解决不确定系统控制问题时的突出特点主要体现在两个方面：一是可处理大范围及复杂结构不确定系统，二是可保证闭环系统具有良好的动态性能。它的核心是根据被控输出和控制输入选择简单的积分串联型为标准型，把系统动态中异于标准型的部分视为“总扰动”，实时估计和消除“总扰动”，从而把具有扰动、不确定性和非线性的被控对象还原成标准的积分串联型。它由三部分组成：跟踪微分器(TD)、扩张状态观测器(ESO)和非线性状态误差反馈控制器(NLSEF)[12]，主要通过TD对输入信号快速有效地跟踪，ESO观测出系统模型的内扰和外扰的影响，再采用前馈补偿的方法通过NLSEF将被控对象转化为简单的积分串联型系统，实现改善系统控制效果的目的。本文采用的控制器为二阶自抗扰控制器，其基本结构见图4。

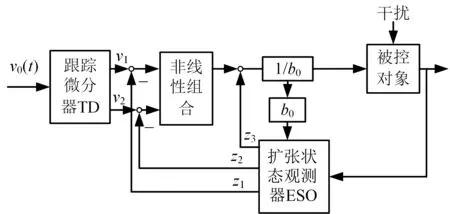
图4 二阶自抗扰控制器基本结构Fig.4 The basic structure of two order ADRC

3.1.1跟踪微分器(TD)

TD是一个信号处理环节，是参数输入的过渡过程，在电驱动海洋绞车系统的升沉补偿过程中，它可以实现对输入信号即母船的升沉速度的跟踪，同时对输入的给定信号进行预处理，解决了响应速度和超调性之间的矛盾。其算法如下：

其中，非线性函数fhan()的表达式为

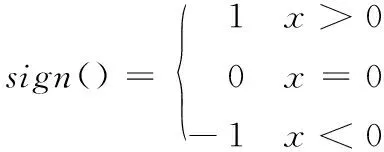
式中，v(k)为输入信号；v1(k)、v2(k)分别为v(k)的跟踪信号和近似微分信号；参数rv、h分别为速度因子和滤波因子。

3.1.2扩张状态观测器(ESO)

ESO是自抗扰控制器的核心，在电驱动海洋绞车系统的升沉补偿过程中，ESO的作用是对所接收到的重物的位置信号进行补偿，它既可以解决模型的未知部分和外部扰动对被控对象的影响，又能将非线性的不确定性转化为线性对象，对未建模动态和外扰进行补偿。其算法如下：

e=z1(k)-y(k)

其中，非线性函数fal(u,a,δ)表达式为

式中，β1、β2、β3为输入误差校正增益；z1、z2为跟踪输出，z3用来估计被控对象扰动量并反馈到控制量v0；δ>0。

3.1.3非线性校正器(NLSEF)

NLSEF给出非线性系统的动态反馈线性化，通过函数的非线性组合将TD输入和ESO输出形成的误差量生成一个控制量，然后传递给被控对象。其算法如下：

式中，e1、e2为状态误差；u为实际控制量；-z3(k)/b0为补偿量。

3.2 主动升沉补偿自抗扰控制系统Simulink模型

由于电驱动海洋绞车所在环境的时变性和其他非线性因素的影响，还有海浪等外界因素对母船的干扰，这些因素会对电驱动海洋绞车控制系统控制器的鲁棒性和稳定性提出较高要求[13]，故本文采用自抗扰控制器对电驱动海洋绞车系统进行控制，实现对电驱动海洋绞车的升沉补偿。以母船的升沉速度v0(t)作为输入，重物位移z(t)作为输出，封装电驱动海洋绞车模型作为被控对象，建立电驱动海洋绞车主动升沉补偿控制系统Simulink仿真模型，并结合PID控制进行对比，其仿真模型见图5。

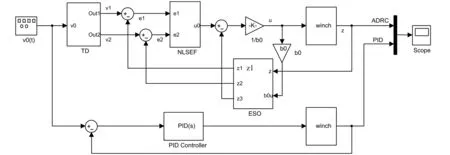
图5 电驱动海洋绞车主动升沉补偿控制系统Simulink仿真模型Fig.5 The Simulink simulation model of active heave compensation control system for electric driven marine winch

4 主动升沉补偿自抗扰控制系统仿真分析

4.1 仿真参数与结果

(1)模型输入。本文考虑4级海况下波浪补偿，波高H取2 m，周期T取5 s，升沉位移与波高比值μ取0.5，代入式(2)，可得母船的升沉速度，作为电驱动海洋绞车主动升沉补偿控制系统的输入。

(2)电驱动海洋绞车系统模型。电驱动海洋绞车系统模型参数取值如下：下放缆绳长度l=2 100 m、缆绳直径dc=32 mm、重物质量m=3 000 kg，其他绞车参数取值见表1，电机参数取值见文献[11]，并将其代入式(18)和式(22 )，计算出变频电机到卷筒以及卷筒到重物的传递函数，得到电驱动海洋绞车系统模型。

(3)控制器参数整定。自抗扰控制器参数比较多，一般情况下，对于非线性参数，如ESO中的{a1,a2,δ}和NLSEF中的{a1,a2,δ0}，都根据经验取固定值。对于幂参数ai，一般在ESO中取a1=0.5，a2=0.25；在NLSEF中取01.0，一般取a1=0.75或0.5，a2=1.25或1.5[14]。δ、δ0会影响自抗扰的非线性性能，如果取得较大，自抗扰可能只会在线性区工作；但如果取得较小，就会产生振颤现象。所以对于ai，本文选取ESO中：a1=0.5，a2=0.25，NLSEF中：a1=0.5，a2=1.5；对于δ、δ0，本文选取δ=δ0=0.1。对于其他参数，先对TD和ESO的参数按照“分离原理”进行整定，调节取得较好效果后再对NLSEF采用整体整定的原则，调节出一组控制效果较好的参数。对PID控制器用“试凑法”调节出一组控制效果较好的参数。参数结果见表2。

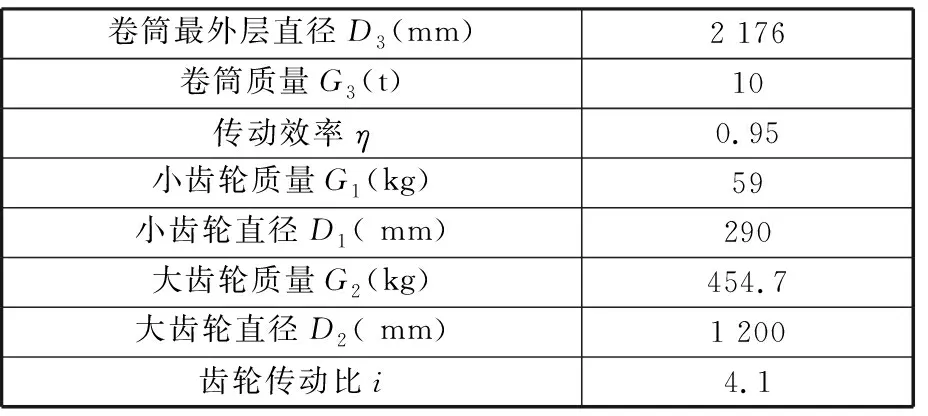
表1 绞车设计参数

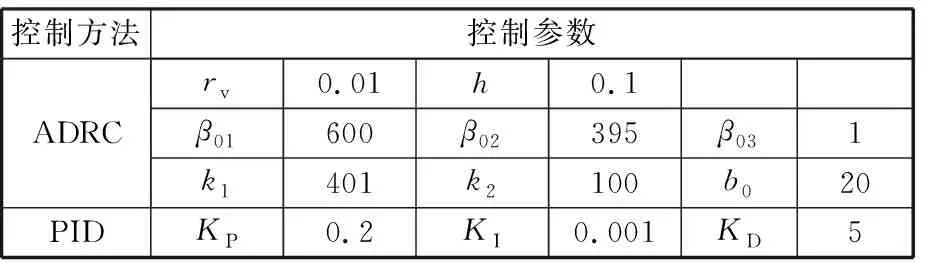
表2 ADRC和PID控制参数

(4)仿真结果。按上述方法整定好自抗扰控制器和PID控制器参数后，运用图5的电驱动海洋绞车主动升沉补偿控制系统Simulink仿真模型进行仿真，仿真结果见图6。为了更好地显示自抗扰控制器和PID控制器的补偿效果，在仿真图中增加母船位移和未加控制时的重物位移进行对比，仿真结果见图7。自抗扰和PID的调节时间、补偿精度、未加控制和加控制的重物位移幅值比的数据比较结果见表3。

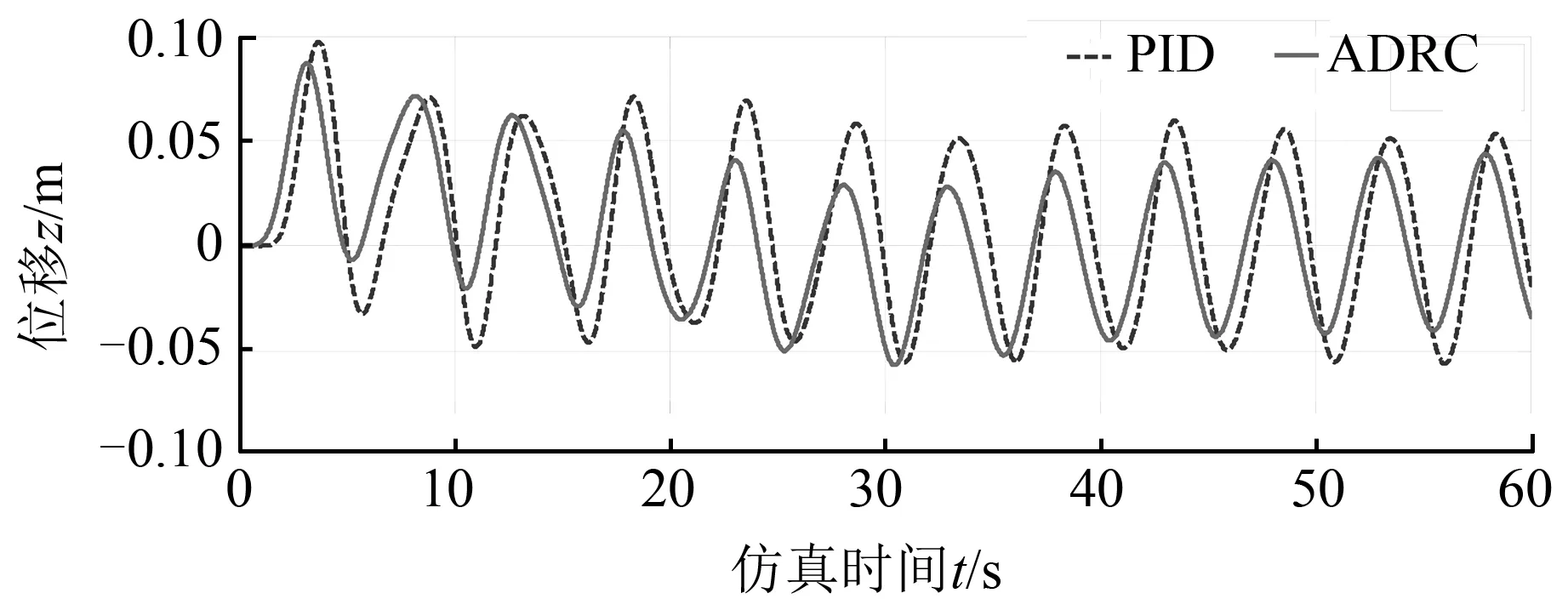
图6 电驱动海洋绞车主动升沉补偿控制系统仿真结果Fig.6 The simulation results of active heave compensation control system for electric driven marine winch

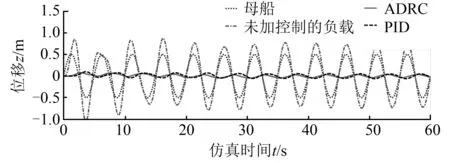
图7 对比仿真结果Fig.7 The contrast simulation results

控制方法调节时间(s)补偿精度(m)未加控制与加控制的重物位移幅值比(%)ADRC250.045.3PID300.068.0

由图6可以看出，在自抗扰控制器和PID控制器的控制下，前5个周期内幅度、振荡周期变化较大，后期重物运动逐渐稳定，这是由于控制器虽然起到了控制作用，但是其调节需要一定的时间，所以前期振荡较大，后期逐渐稳定。自抗扰控制的补偿精度为0.04 m，调节时间为25 s；PID控制的补偿精度为0.06 m，调节时间为30 s，自抗扰控制比PID的补偿效果提高了30%以上，调节时间比PID提前了5 s。由此说明，自抗扰控制的响应速度快，调节时间短，调节效果较好；PID的响应速度慢，调节时间长，调节效果较差。由图7可以看出，重物位移幅值比母船运动位移幅值大，且稍有滞后，这是由于缆绳较长且在重物的作用下有一定的伸长量，当母船从波峰往下回落时，重物还存在一个向上的运动速度，会继续往上移动一定距离，重物回落需要一定的时间，所以重物位移幅值比母船运动位移幅值大，且在时间上有所滞后。结合图5可以看出，施加控制后的补偿效果明显比未加控制时好，自抗扰控制时，滞后时间为2 s，未加控制与施加控制的重物位移幅值比为5.3%；PID控制时，滞后时间为3 s，未加控制的重物位移与施加控制的幅值比为8.0%。由此说明，控制系统加了自抗扰控制器后，虽然过渡时间稍有滞后，但是总体的调节质量较好，且比PID控制器的补偿效果好，证明了自抗扰控制器的先进性，它可以使升沉补偿控制达到较好的效果。

4.2 仿真分析

本文考虑的是4级海况下的主动升沉补偿，由于海况是变化的，不同海况等级会改变母船的升沉位移，从而改变重物的位移量，且不同海况对母船的位移影响较大，所以将自抗扰控制器和PID控制器在四级海况下的控制器参数应用于3级和5级海况，且不随海况的变化而变化，比较不同海况下自抗扰控制和PID控制对电驱动海洋绞车升沉补偿控制系统的控制效果。

电驱动海洋绞车系统的模型参数也是变化的，当绞车以一定速度下放缆绳时，会使重物不断下降，在其下降过程中，不同下放深度、不同缆绳直径、不同重物质量等都会影响重物位移的幅值和振荡周期。选取下放缆绳长度、缆绳直径、重物质量作为3个影响因素，分别代入式(18)和式(22)，计算出变频电机到卷筒以及卷筒到重物的传递函数，得到不同的电驱动海洋绞车系统Simulink模型，并进行仿真分析。由于3个模型参数均会改变电驱动海洋绞车控制系统模型，在分析某个具体模型参数对控制效果的影响时，只改变该模型参数，其余模型参数保持不变，模型输入仍为4级海况，并且自抗扰控制器参数和PID控制器参数取4.1节中整定好的参数，在电驱动海洋绞车系统模型改变时，控制器参数保持不变。

4.2.1不同海况时仿真分析

3级海况有效波高H的范围为[0.5 m, 1.25 m]，波高H取1 m，周期T取4 s，升沉位移与波高比值μ为0.5，代入式(2)，可得母船的升沉速度，作为电驱动海洋绞车主动升沉补偿控制系统的3级海况输入。同理，5级海况有效波高H的范围为[2.5 m, 4.0 m]，波高H取3.5 m，周期T取10 s，升沉位移与波高比值μ为0.5，代入式(2)，可得母船的升沉速度，作为电驱动海洋绞车主动升沉补偿控制系统的5级海况输入。

不同海况时的补偿效果仿真结果见图8，补偿精度、重物位移与波高的幅值比数据比较结果见表4。由图8和表4可见，随着海浪级数的增大，其周期变大，幅值增加，母船的升沉运动也会加剧。在自抗扰控制下，3级海况时补偿精度为0.02 m，重物位移与波高的幅值比为2.0%；4级海况时补偿精度为0.045 m，重物位移与波高的幅值比为2.25%；5级海况时补偿精度为0.06 m，重物位移与波高的幅值比为2.0%。虽然不同海况的幅值变化较大，但是自抗扰控制后幅值比变化不大。在PID控制下，3级海况时补偿精度为0.045 m，重物位移与波高的幅值比为4.5%；4级海况时补偿精度为0.055 m，重物位移与波高的幅值比为2.75%；5级海况时补偿精度达到0.1 m，重物位移与波高的幅值比为3.5%，PID控制下幅值比变化较大，并且在4级海况下幅值比最小，说明在不同海况下，只能通过被动改变PID

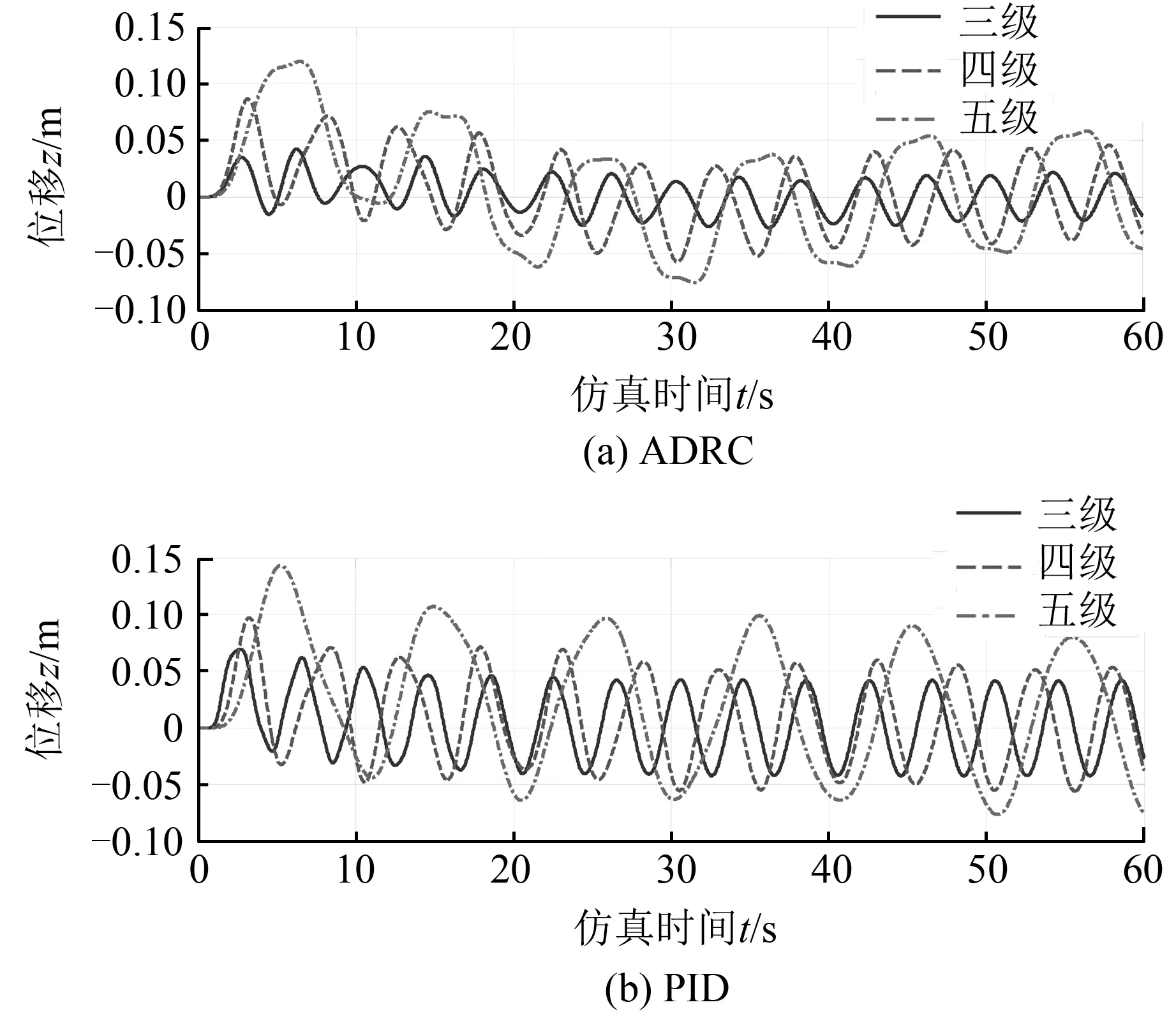
图8 不同海况时的补偿效果Fig.8 The compensation effect in different sea states

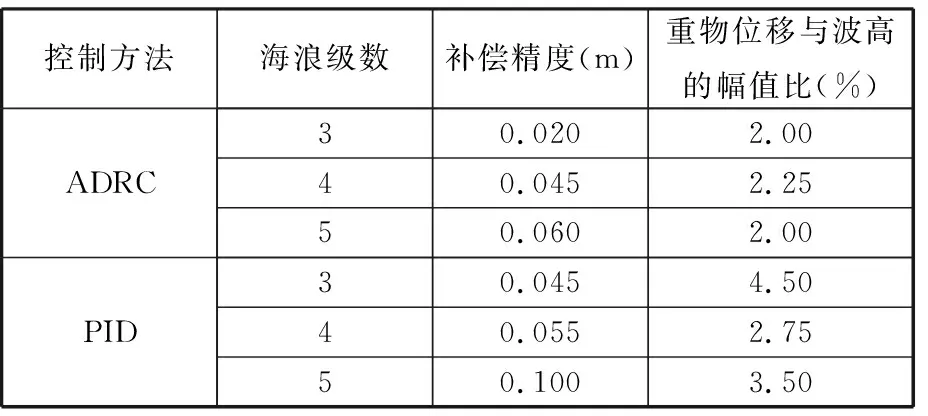
表4 不同海况时数据比较结果

参数来达到较好控制效果。由此说明，在海况变化时，自抗扰控制器的同一组参数对不同海况有很好的升沉补偿效果，PID控制器的同一组参数的补偿效果较差。

4.2.2不同下放深度时仿真分析

重物下放的过程中，下放深度不断变化，即电驱动海洋绞车控制系统模型会不断改变，下放缆绳长度l分别取700 m、2100 m、3500 m，补偿效果见图9，补偿精度数据比较结果见表5。由图9和表5可见，在自抗扰控制下，前25 s随着下放深度的变化，重物响应位移有所变化，后期控制效果稳定后，重物响应位移大体不变，系统补偿精度基本稳定在45 mm。在PID控制下，重物下放深度为700 m和2 100 m时重物响应位移相差不大；深度为700 m时，系统补偿精度为0.07 m；深度为2 100 m时，系统补偿精度为0.06 m；深度为3 500 m时，补偿效果较差。15 s时系统补偿精度达到0.18 m，虽然30 s后系统补偿精度稳定在0.08 m，但是40 s后，系统补偿精度又达到0.17 m，由此可见：下放深度为700 m时，自抗扰控制比PID控制的补偿效果提高了35%以上；下放深度为2 100 m时，自抗扰控制比PID控制的补偿效果提高了30%以上；下放深度为3500 m时，自抗扰控制比PID控制的补偿效果提高了70%以上。同时可以看出，下放深度为2 100 m时，PID的控制效果是最好的，这是由于控制器参数是在电驱动海洋绞车控制系统模型参数(l=2 100 m、m=3 000 kg、dc=32 mm)时整定得到的，所以在这组模型参数下的控制效果是最好的，说明不同模型下，都应对PID控制器的参数进行调节才能达到较好的控制效果。由此说明，下放深度发生变化时，自抗扰控制器的同一组参数有很好的补偿效果，PID控制器的同一组参数的补偿效果较差。

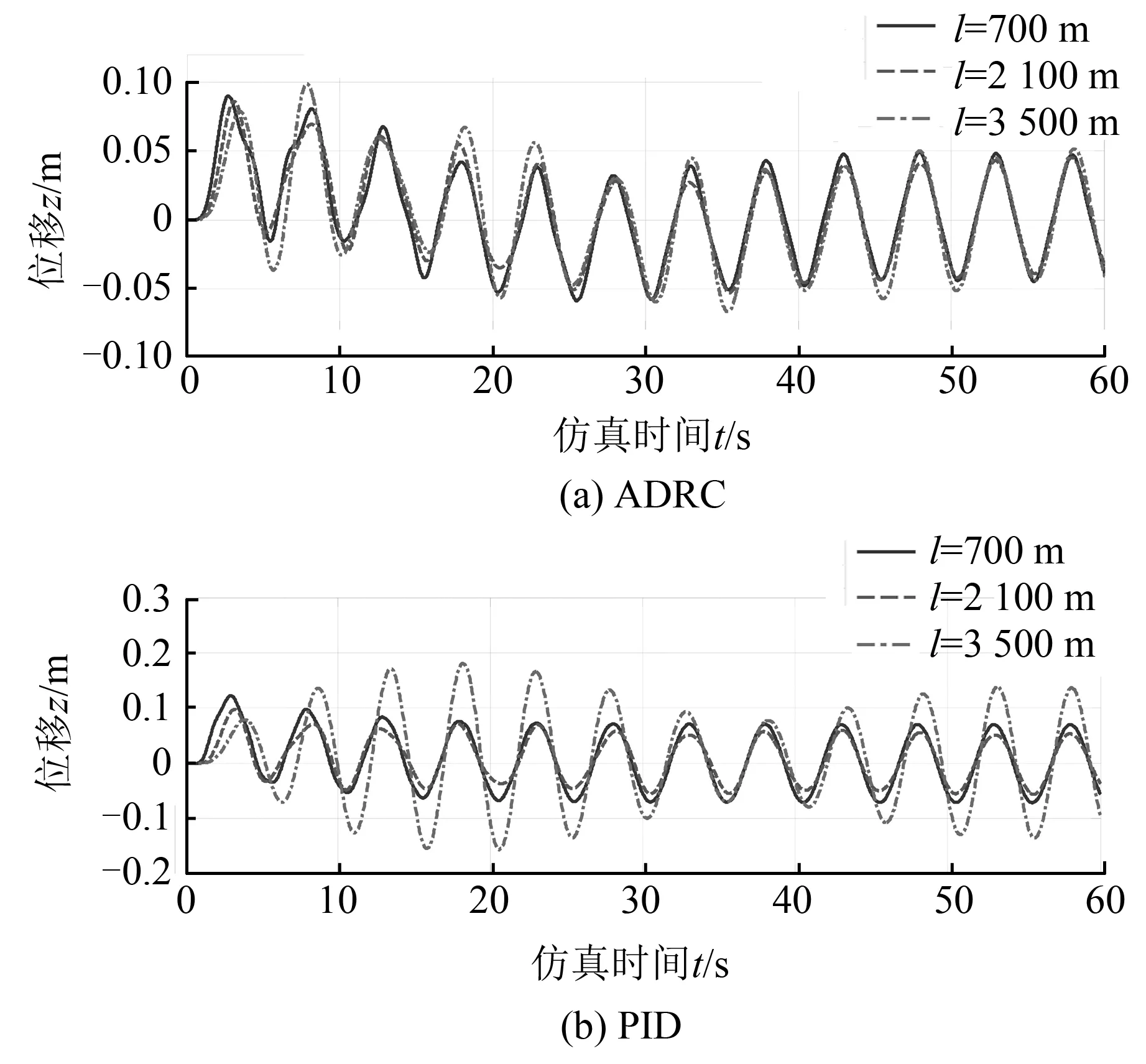
图9 不同下放深度时的补偿效果Fig.9 The compensation effect at different transfer depth

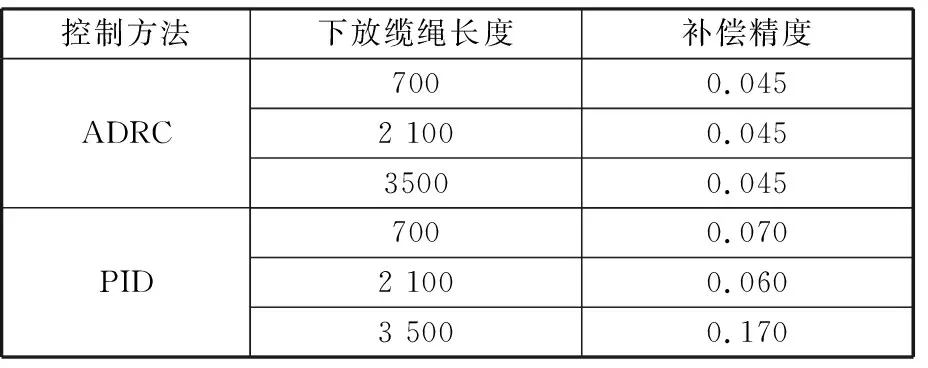
m

4.2.3不同缆绳直径时仿真分析

当缆绳的直径不同时，电驱动海洋绞车控制系统模型也会不断改变，缆绳直径dc分别取20 mm、32 mm、44 mm，仿真结果见图10，补偿精度数据比较结果见表6。由图10和表6可见，缆绳直径越大，重物位移幅值越小，这是由于没有控制器控制时，缆绳直径越大，其弹性刚度系数、等效质量均越大，所以重物运动位移幅值越小，加入控制器控制后，其控制效果也随之变化。在自抗扰控制下，重物响应位移大体不变，直径为20 mm时， 系统补偿精度为0.05 m； 直径为32 mm

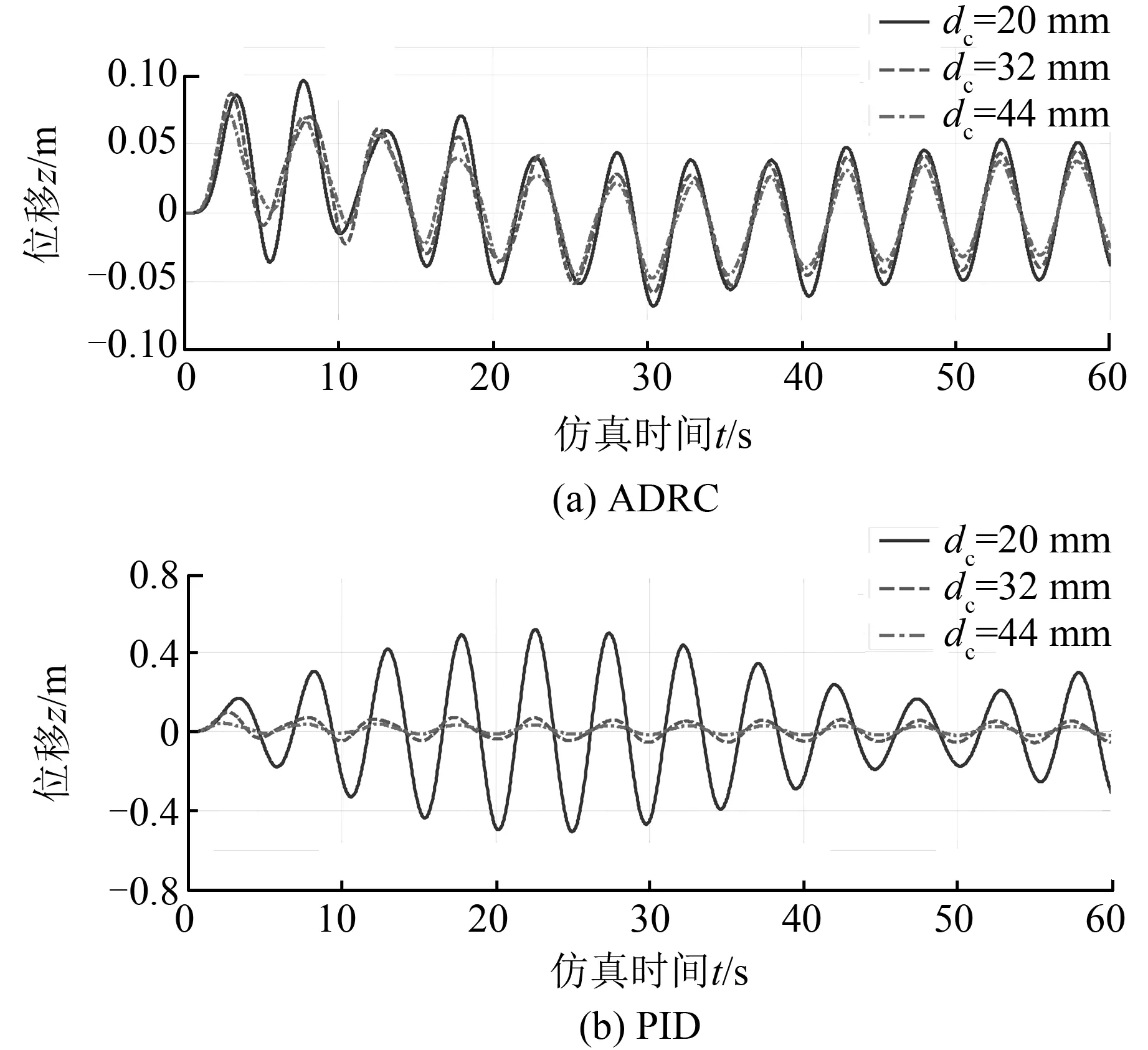
图10 不同缆绳直径时的补偿效果Fig.10 The compensation effect of different cable diameters

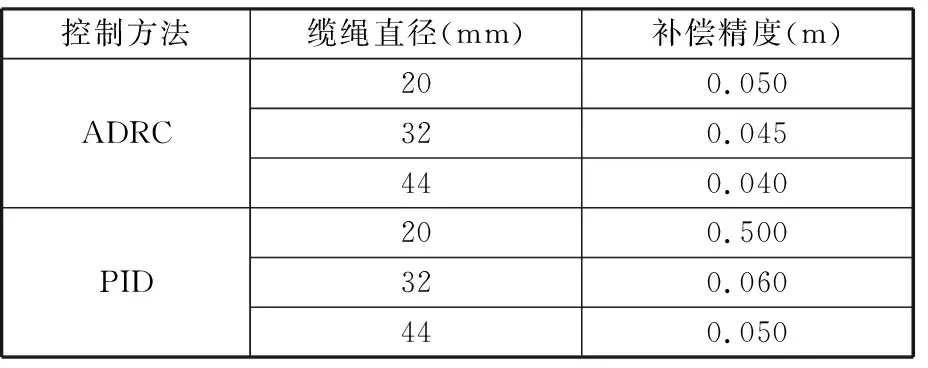
控制方法缆绳直径(mm)补偿精度(m)ADRC200.050320.045440.040PID200.500320.060440.050

时，系统补偿精度为0.045 m；直径为44 mm时，系统补偿精度为0.04 m。在PID控制下，缆绳直径为32 mm和44 m时重物响应位移变化不大，直径为32 mm时，系统补偿精度为0.06 m；直径为44 mm时，系统补偿精度为0.05 m；直径为20 mm时，补偿效果较差。20 s时系统补偿精度达到0.5 m，虽然50 s后系统补偿精度控制在0.2 m，但是55 s后，系统补偿精度又达到0.3 m，基本上没有补偿效果。由此可见：缆绳直径为20 mm时，自抗扰控制比PID控制的补偿效果提高了15%以上；缆绳直径为32 mm时，自抗扰控制比PID控制的补偿效果提高了30%以上；缆绳直径为44 mm时，自抗扰控制比PID控制的补偿效果提高了85%以上。由此说明，在缆绳直径发生变化时，自抗扰控制器的同一组参数有很好的补偿效果，PID控制器的同一组参数的补偿效果较差。

4.2.4不同重物时仿真分析

当需要对不同重物进行下放时，其质量会随重物的不同而变化，即电驱动海洋绞车控制系统模型会不断改变，重物质量m分别取1 000 kg、3 000 kg、5 000 kg时，仿真结果见图11，补偿精度数据比较结果见表7。由图11和表7可见，在自抗扰控制下，重物响应位移大体不变，系统补偿精度基本稳定在45 mm；在PID控制下，重物响应位移变化也不大，质量为1 000 kg时，系统补偿精度为0.05 m；质量为3 000 kg时，系统补偿精度为0.06 m；质量为5 000 kg时，系统补偿精度为0.07 m。由此可见：重物质量为1 000 kg时，自抗扰控制比PID控制的补偿效果提高了10%以上；重物质量为3 000 kg时，自抗扰控制比PID控制的补偿效果提高了30%以上；重物质量为5 000 kg时，自抗扰控制比PID控制的补偿效果提高了35%以上。由此说明，在重物质量发生变化时，自抗扰控制器的同一组参数有很好的补偿效果，PID控制器的同一组参数的补偿效果较差，但在一定范围内，重物质量这一模型参数的变化对控制效果影响不大。

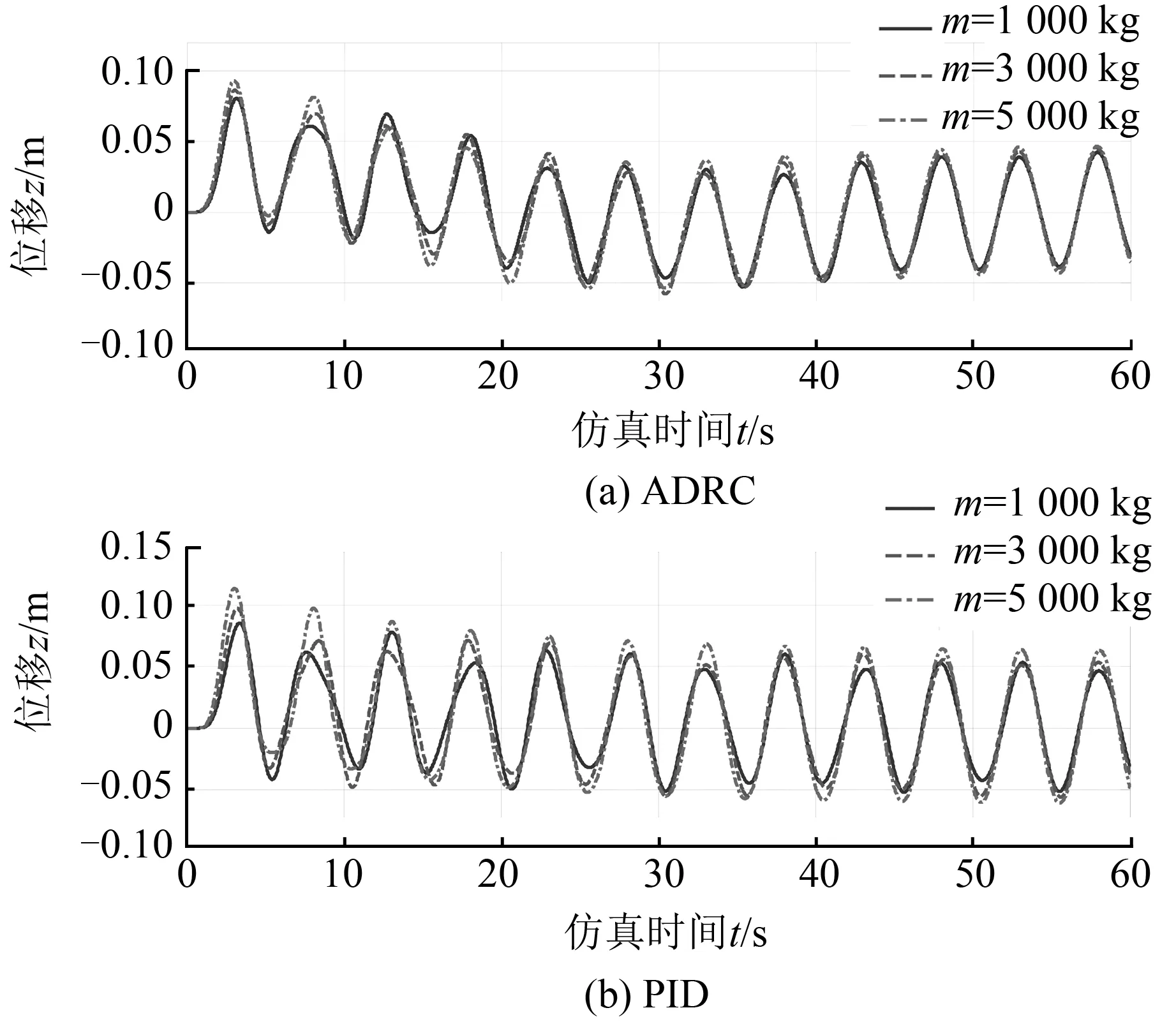
图11 不同重物时的补偿效果Fig.11 The compensation effect of different heavy objects

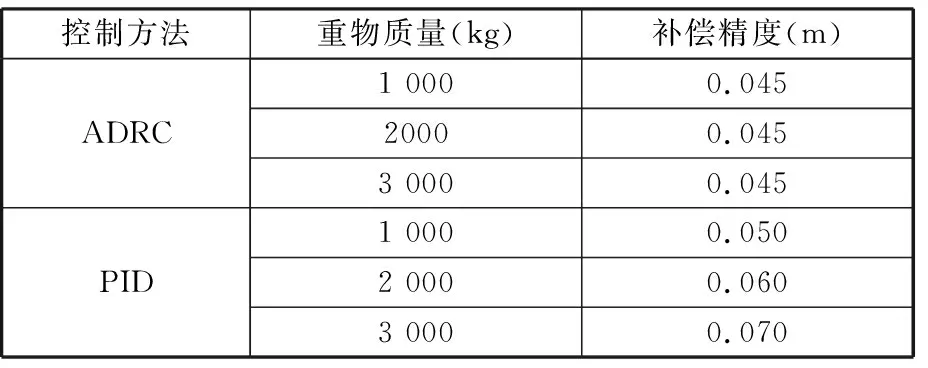
控制方法重物质量(kg)补偿精度(m)ADRC1 0000.04520000.0453 0000.045PID1 0000.0502 0000.0603 0000.070

综上所述，海况、模型均相同时，自抗扰控制器比PID控制器的响应速度更快，调节时间更短，调节效果更好。海况发生变化时，自抗扰控制器的同一组参数控制下有较好的控制效果，具有很好的鲁棒性；模型发生变化时，自抗扰控制器对模型变化不敏感，能够有效地观测到系统参数变化引起的模型的变化，主动估计并且补偿系统的动态变化，说明其控制参数在一定范围内，具有一定的通用性，它被用于控制不同的模型时均可取得较好的控制效果。而PID控制器的同一组参数应用于不同海况和不同模型时控制效果较差，说明在不同海况和模型下，都应对PID控制器的参数进行调节，所以只能通过被动改变其参数来进行补偿。因此，当海况和电驱动海洋绞车参数发生变化时，在控制器的同一组参数控制下，自抗扰控制器比PID控制器的鲁棒性更强，抗干扰能力更好，将其应用到电驱动海洋绞车升沉补偿控制系统中，可以取得很好的控制效果。

5 结论

(1)当海况和电驱动海洋绞车控制系统模型相同时，通过对比发现自抗扰控制器比PID控制器的响应速度更快，调节时间更短，调节效果更好。

(2)电驱动海洋绞车控制系统模型参数会随重物下放深度、缆绳直径、重物质量等的变化而变化，将自抗扰控制引入电驱动海洋绞车系统中，可以在模型参数发生变化时，对系统有较好的控制效果，在不同海况下，自抗扰控制器的补偿效果也较好。因此，自抗扰控制器比PID控制器的鲁棒性强，抗干扰力好，能更有效地为电驱动海洋绞车主动升沉补偿控制提供理论依据。