液压缸非线性弹簧力下的轧机特性及控制
刘 彬 潘贵翔 李 鹏 姜甲浩 刘 爽 刘兆伦
1.燕山大学电气工程学院,秦皇岛,066004 2. 燕山大学信息科学与工程学院,秦皇岛,066004
0 引言
板带轧机在重工业机械领域发挥着重要的作用,随着科技的飞速发展,高端领域对板带轧机的要求越来越高[1]。然而板带轧机辊系在工作过程中经常发生振动,影响轧制产品的质量和生产效率,很难达到现在高端领域对轧制产品的要求,严重时损坏轧制设备,造成经济损失,在很大程度上限制了轧制产业的快速发展[2-4]。
板带轧机振动问题的研究已经持续了近半个世纪,国内外学者从不同角度进行了分析研究。文献[5]研究了张力对轧机非线性振动的影响,通过改变外激频率分析轧机振动系统的稳定性,得出轧制速度和带钢厚度对系统稳定性有很大影响的结论。文献[6]研究了轧辊与液压缸之间的分段非线性因素,通过建立轧机单自由度分段非线性垂直振动模型,发现分段非线性约束可能是导致轧机颤振发生的一个原因。文献[7]考虑轧件和轧辊间的相互作用, 建立了基于辊缝动态摩擦方程的轧机辊系垂直振动模型,研究了轧件-轧辊工作界面动态摩擦机制影响下的冷轧机辊系垂振机理及系统稳定性。文献[8]引入Duffing振子和参激刚度项,建立了轧机辊系垂直振动模型,仿真分析了轧机辊系振幅在非线性参数变化下的分岔特性。文献[9-10]认为速度改变引起液压缸内部摩擦因数的变化,动态载荷引起液压缸等效刚度的变化,摩擦因数和等效刚度的变化都会使液压缸产生非线性。以上研究主要对入口张力、轧件和轧辊的相互作用以及液压缸摩擦力对轧机辊系振动的影响进行了分析,没有给出抑制消除轧机辊系垂直振动的具体方法。
笔者以轧机辊系为研究对象,考虑液压缸非线性弹簧力,建立非线性约束作用下的轧机辊系振动模型。通过仿真分析轧机辊系振动的特性规律,引入吸振器控制装置,研究吸振器的质量、弹簧力和摩擦力对控制轧机辊系振动行为的影响。
1 轧机辊系振动模型
1.1 非线性弹簧力
液压弹簧刚度是指液压缸工作腔完全封闭时,在外力作用下,油液体积被压缩后所形成的液体非线性弹簧刚度。本文以轧机工业中常用的双作用单活塞液压缸为研究对象进行分析,图1为双作用单活塞液压缸的结构图。
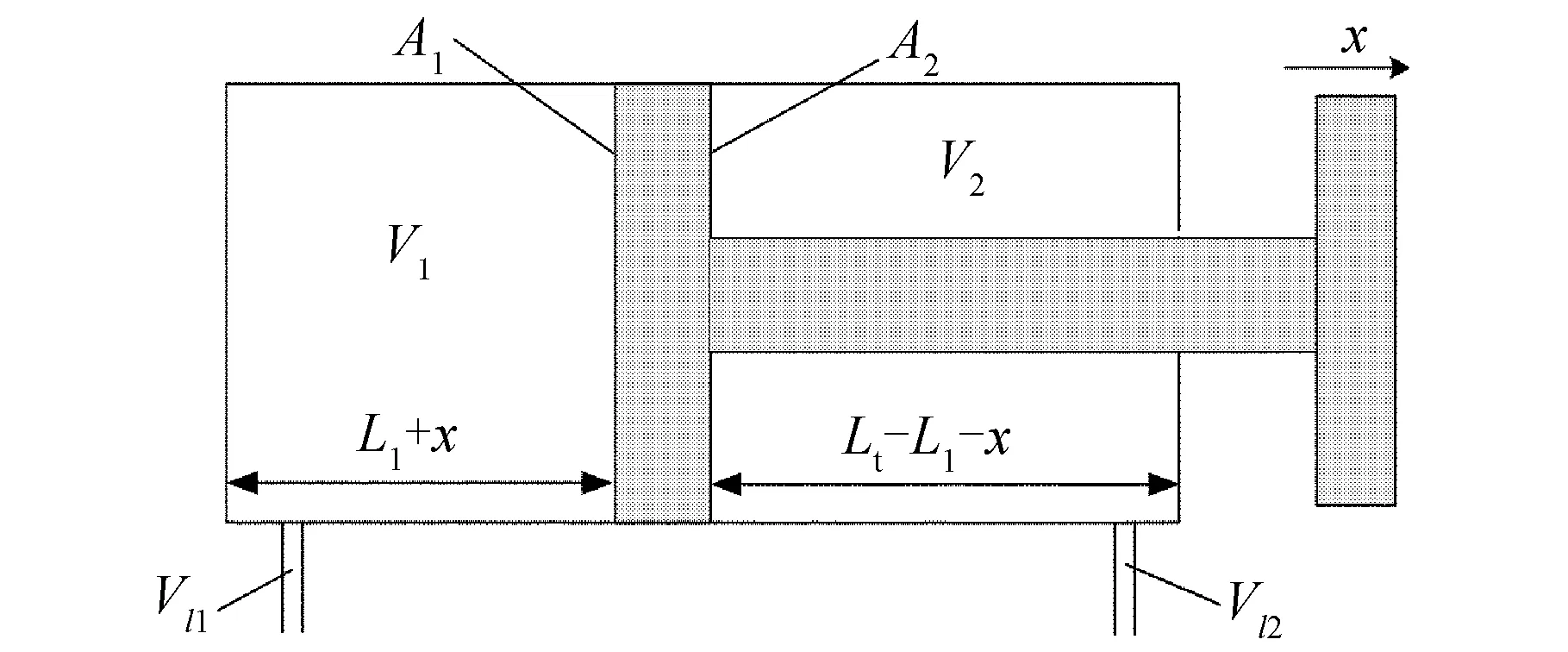
图1 双作用单活塞液压缸的结构图Fig.1 Structural diagram of double acting single piston hydraulic cylinder
轧机液压缸的弹簧刚度由液压油刚度和活塞杆刚度串联组成[11]。活塞杆的体积模量是液压油体积模量的近百倍,所以把活塞杆视为刚体,液压缸的非线性刚度主要由液压油的刚度决定[12]。两腔油液始终存在压力并均处于压缩状态,而且两腔油液是同时起作用的,因此液压缸总液压弹簧刚度可等效为两腔液压弹簧刚度的并联[13]:
(1)
式中,K为液压缸油液体积弹性模量;A1、A2分别为液压缸无杆腔和有杆腔的活塞侧有效面积;L为液压缸总行程;L1为活塞杆初始位置;Vl1、Vl2分别为进油阀与无杆腔之间油管内油液体积和进油阀与有杆腔之间油管内油液体积,它们相对于两油腔体积很小;x为液压缸活塞杆的振颤位移。
则原点x=0处k(x)展成的泰勒级数为
(2)
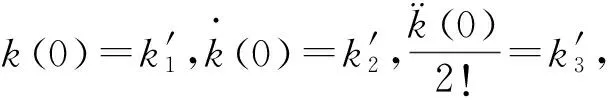
(3)
非线性弹簧力为
(4)
对式(4)积分,由于弹簧弹性势能Ep具有对称性,故忽略奇次幂项,即有
(5)
对式(5)求导,则液压缸的弹簧力可表示为
(6)
1.2 非线性弹簧力约束下的轧机辊系振动模型
根据非线性动力学的观点,研究轧机液压缸系统的非线性弹簧力动态特性对轧机辊系振动的影响[14],根据轧机的机械结构可以简化轧机辊系的结构,如图2所示。
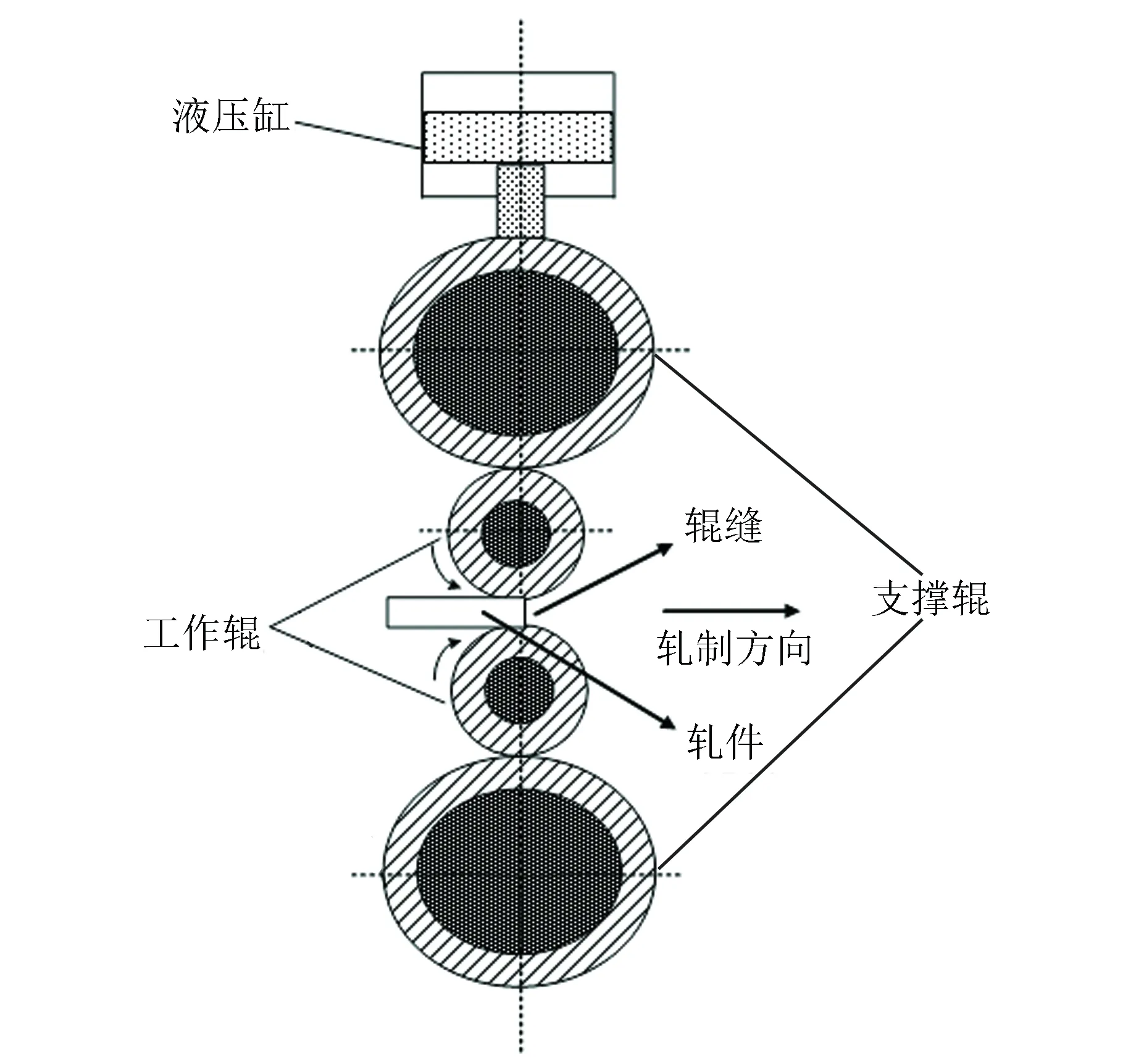
图2 四辊轧机结构简图Fig.2 Structural diagram of four high mill
为简化研究,只对轧机上部辊系进行分析,建立一种液压缸非线性弹簧力约束下的轧机辊系振动模型,其振动模型如图3所示。
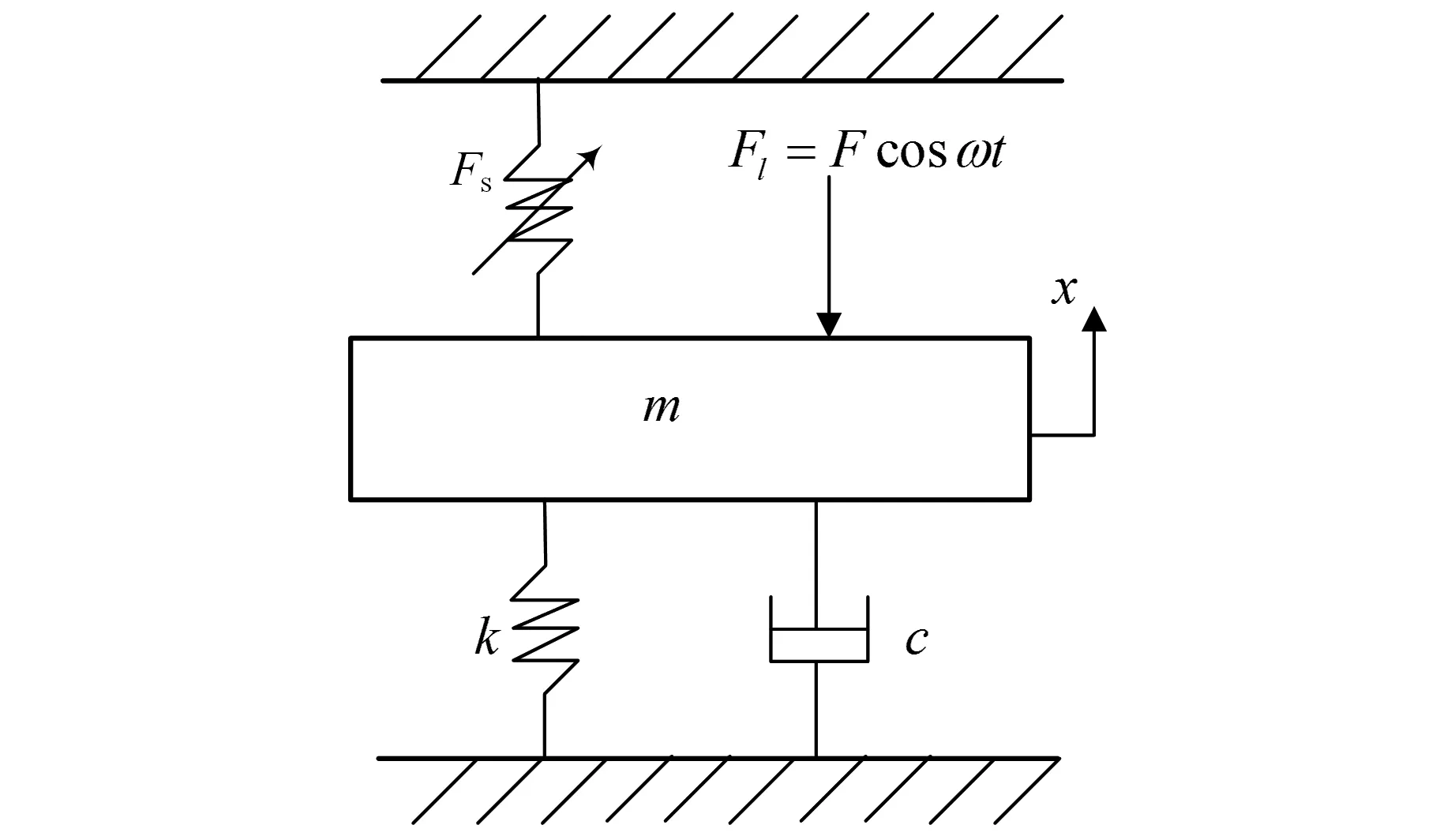
图3 轧机辊系振动模型Fig.3 Roll system vibration model of rolling mill
根据广义耗散拉格朗日原理,建立轧机辊系垂直振动动力学方程:
(7)
式中,m为四辊轧机上支承辊、上工作辊及其轴承座的等效质量;c为轧机系统轧件的等效阻尼;k为轧机系统轧件的等效刚度;F为等效负载力。
为了研究不同非线性约束对轧机辊系振动行为的影响,给方程非线性弹簧力冠以系数α。
2 轧机辊系动态响应
为了方便计算,将动力学方程式(式(7))化简为
F*cosωt
(8)
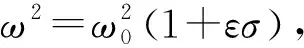
(9)
αx[ρ1+ρ2+(γ1+γ2)x2]
(10)
式中,ε为非线性项系数;σ为频率调谐因子。
当ε=0时,式(8)的派生系统为线性保守系统,导出派生系统的解及其导数:
(11)
(12)
(13)
φ=ωt-θ
式中,a、θ为时间的慢变函数。
将式(10)代入式(13)得
(14)
将式(14)代入式(12)得
(15)

0.75αa2(γ1+γ2)]2
(16)
式(16)为轧机辊系振动系统的幅频特性方程,是研究轧机液压缸非线性约束下轧机辊系振动的基础。
3 轧机辊系振动行为特性
以某厂板带轧机参数为例,对液压缸非线性作用下的轧机辊系垂直振动模型进行数值仿真求解。通过理论研究,探索液压缸非线性弹簧力和摩擦力等非线性因素对轧机辊系动力学特性的影响规律。系统模型中的参数取值如表1所示。

表1 轧机辊系振动参数
3.1 频域特性
轧机辊系振动规律受不同轧制参数的影响,采用表1所列参数对系统幅频特性进行仿真,分析活塞杆初始位移和液压缸非线性弹簧力对轧机辊系振动规律的影响。
图4为轧机液压缸活塞杆不同初始位移的幅频特性曲线,可以看出,幅频特性曲线对活塞杆初始位移的变化非常敏感,当初始位移稍微减小,系统的幅频曲线右移,轧机固有频率小幅变大,同时幅频特性曲线的弯曲度也变大,即系统的不稳定区域变宽。在工艺允许的范围内,适当调整轧机活塞杆初始位移可以增强系统的稳定性。

图4 不同初始位移的幅频特性Fig.4 Amplitude frequency characteristics of different initial displacements
比较图5中不同非线性弹簧力系数曲线发现,随着非线性弹簧力系数α的增大,系统的幅频曲线右移,轧机固有频率变大,同时幅频特性曲线的弯曲度也变大,系统的不稳定区域变宽,轧机辊系的轧制过程会因此而更易于失稳。

图5 非线性弹簧力系数对幅频特性曲线的影响规律Fig.5 Influence law of nonlinear spring force coefficient on amplitude frequency characteristic curve
3.2 分岔特性
以外激励幅值作为分岔参数,分析系统分岔响应随外激励幅值的变化规律,研究外激励幅值对系统稳定性的影响。
由图6可知:外激励取不同值时,系统发生了不同程度的分岔现象,在分岔图上出现单值曲线、多值曲线和无穷多值曲线;系统方程存在单解、多解和无穷解,即轧机辊系振动在单周期运动、倍周期运动和混沌运动等之间交替变化。外激励F=591 kN时的仿真结果如图7所示,相轨迹在有限区域内重复,呈一封闭曲线,Poincare截面上只有一个孤立的点,说明此时轧机辊系振动系统为周期运动状态。外激励F=601.2 kN时的仿真结果如图8所示,相轨迹仍在有限区域内重复,呈一封闭曲线,从局部放大图中可以看出,此时轧机辊系振动有2个振动速度,Poincare截面上有2个孤立的点,说明此时轧机辊系振动系统为2倍周期运动状态。外激励为F=627 kN时的仿真结果如图9所示,相轨迹不再是一封闭曲线了,Poincare截面上变现为离散的点,说明此时的轧机辊系振动系统处于混沌运动状态。
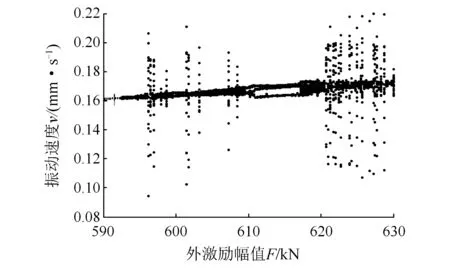
图6 轧机辊系的分叉特性Fig.6 Bifurcation characteristics of mill roll system
图7 F=591kN时的1倍周期运动Fig.7 One times periodic motion at F=591 kN

图8 F=601.2kN时的2倍周期运动Fig.8 Two times periodic motion at F=601.2 kN

图9 F=627kN时的混沌运动Fig.9 Chaotic motion at F=627 kN
4 轧机辊系振动控制
4.1 吸振器控制模型建立
轧机吸振器是通过弹性元件和阻尼元件,把辅助质量连接到轧机主系统(轧机支架)上的减振装置,吸振器安装到轧机辊系后,二者构成一个两自由度系统,减振器在空间和结构上的安装情况如图10所示。轧机辊系和吸振器装置只做垂直方向的直线运动,系统静止时,轧机上辊系和吸振器装置的平衡位置为运动原点,轧机辊系和吸振器装置的振动位移的大小代表振动强度,减小轧机辊系的振动,就需要减小振动位移。轧机辊系在简谐外激励作用下振动,轧机辊系的振动能量通过吸振器的弹性元件和阻尼元件转移到吸振器装置上。吸振器通过弹性元件和阻尼元件作用在轧机辊系上的作用力,与外界对轧机辊系的作用力方向相反,把轧机辊系的振动能量转化为摩擦力热能和吸振器动能,从而减小轧机辊系的振动位移,达到抑制振动的目的。

图10 安装减振器后的轧机辊系简图Fig.10 Roll diagram of rolling mill after shock absorber installation
如图11所示,在轧机上辊系(等效质量为m1)上安装一个质量为m2的动力吸振器,x1为轧机上辊系的绝对位移,x2为吸振器的绝对位移,k1、c1分别为轧机上辊系和轧件之间的等效刚度和等效阻尼,k2、c2分别为吸振器和轧机上辊系之间的等效刚度和等效阻尼,Fl(t)=Fcosωt为等效负载力,其中,F为外激励幅值,ω为外激励的角频率。
轧机上辊系和吸振器以及轧机上辊系和轧件之间的等效刚度和等效阻尼是线性的,液压缸的弹簧力是非线性的。带吸振器的两自由度系统模型的运动方程为
(17)

图11 带吸振器两自由度系统模型Fig.11 System model of two degrees of freedom with vibration absorber
4.2 带吸振器控制装置的系统响应
式(17)可简化为
(18)
令质量比μ=m2/m1,根据吸振器的最优控制原理可近似得[15]:
式(18)等号右边非线性项冠以系数ε,得
δ=εδ1ξ=εξ1ρ=ερ1F0=εF10
(19)
采用多尺度法求解:引入不同时间尺度T0=t和T1=εt。
对T0=t和T1=εt中的时间t进行求导:
(20)
只研究式(20)的一次近似解,设解x1和x2的形式为
(21)
将式(20)、式(21)代入式(19),使方程两端带有参数ε且同次幂的系数和相等,得到各阶近似方程:
(22)
(23)
将零次近似方程组(式(23))的解写为复数形式如下:
(24)
将式(24)代入一次近似方程组(式(23))的右边得到:
(25)
式中,cc代表左边各项的共轭复数。
考虑内共振情况,假设ω=ω10+εσ,ω20=ω10+εσ1,并将其代入式(25)并消去久期项,可得
(26)
为求解式(26),引入复函数B1=0.5a·exp(iφ1),B2=0.5bexp(iφ2),其中,a、b、φ1、φ2都是时间T1的函数,引入中间变量θ1=φ2-φ1+σ1T1,θ=σT1-φ1,将B1、B2、θ1、θ2代入式(26),令等式两边的实部和虚部相等,可得
(27)
(28)
式(28)为带吸振器轧机辊系振动系统的幅频特性方程,是研究吸振器控制特性的基础。
4.3 吸振器控制特性研究
为了对比吸振器控制装置对轧机辊系振动行为的影响,仿真分析了加入吸振器控制装置前后的时域特性曲线和幅频特性曲线,分析了吸振器控制装置的质量、弹簧力和摩擦力对幅频特性的影响。图 12为加入吸振器控制装置前后的时域曲线,可以看出,吸振器控制装置减小了轧机辊系的振动幅值。
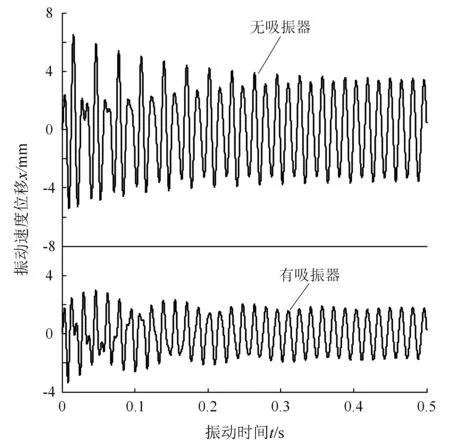
图12 加入吸振器前后时域曲线Fig.12 Time domain curve with and without vibration absorber
图13~图15分别为不同吸振器质量、弹簧力和摩擦力的振动幅频特性曲线。比较图4、图13可以清晰看到,吸振器的加入使轧机辊系的幅频曲线高度减小,说明吸振器控制装置对轧机辊系振动控制的有效性。由图13可以看出,不同吸振器质量对应不同弯曲度和高度的幅频特性曲线,即吸振器质量的大小影响系统的稳定性;由图14可以看出,吸振器弹簧力的改变使幅频特性曲线的弯曲度随之改变,改变了系统稳定的范围;由图15可以看出,吸振器摩擦力的改变使幅频特性曲线的高度发生变化,即吸振器摩擦力影响系统的振动幅值。

图13 不同吸振器质量的幅频特性曲线Fig.13 Amplitude frequency characteristics of different absorbers

图14 不同吸振器弹簧力的幅频特性曲线Fig.14 Amplitude frequency characteristics of spring force of different vibration absorbers

图15 不同吸振器摩擦力的幅频特性曲线Fig.15 Amplitude frequency characteristics of friction force of different vibration absorbers
5 结论
(1)液压缸活塞杆初始位置和非线性弹簧力的改变,影响轧机固有频率的大小和系统的稳定区域的范围。随着活塞杆初始位置的增大,轧机固有频率减小,不稳定区域的范围减小;非线性弹簧力的增大使轧机辊系的不稳定区域变宽,轧机固有频率增大。
(2)为了抑制轧机辊系的振动,本文考虑吸振器在减振过程中的作用,构造了一种带吸振器装置的轧机辊系振动模型,通过吸振器吸收轧机主振动系统的振动能量。通过调整吸振器的质量、刚度及阻尼参数,使吸振器能尽量多地吸收主系统的能量。
(3)不同的吸振器质量、弹簧力和摩擦力对轧机辊系振动幅频特性曲线的幅值和稳定区域有着不同的影响。在一定范围内减小吸振器的质量可以提高系统的稳定性;一定范围内增大吸振器弹簧力可以缩小系统不稳定区域;一定范围内增大吸振器摩擦力可以减小系统的振动幅值。为了提高轧机辊系的稳定性,选取最理想的吸振器质量、弹簧力和摩擦力至关重要。

