基于结构张量的四阶偏微分方程图像降噪模型

王 娜， 刘 祎， 王晓旭， 杨冠儒， 桂志国

(1. 中北大学 山西省生物医学成像与影像大数据重点实验室， 山西 太原 030051；2. 中北大学 信息与通信工程学院， 山西 太原 030051； 3. 中北大学 环境与安全工程学院， 山西 太原 030051；4. 北京工业大学 信息与通信工程学院， 北京 100022)

0 引 言

随着计算机和网络技术的高速发展， 人类已步入数字图像时代. 数字图像在采集、 压缩、 传输和储存过程中往往会受到成像设备和外界环境等诸多因素的干扰而导致图像失真. 图像失真主要表现为图像模糊、 图像结构信息被噪声淹没等， 失真后的图像已不能真实地反映原始图像的信息， 这样给图像的后期处理如图像增强、 图像分割、 边缘检测等带来困难， 因此图像去噪和图像去模糊在图像处理研究领域中是最基础和最重要的环节. 近年来， 基于变分和偏微分方程( PDE) 方法在图像处理中得到了广泛的应用[1]. 其中最著名的是由Perona 和Malik[2]所提出的基于偏微分的各向异性扩散模型， 即PM模型， 该模型是偏微分方程在图像恢复领域的开创性工作. PM模型定性地采用关于梯度模值的函数作为边缘检测函数来自适应地控制图像的边缘区域和非边缘区域的扩散强度. 迄今为止， PM模型仍被众多学者所关注， 不断对其进行深入研究， 在图像分割、 图像去噪、 边缘检测、 修复和图像增强等许多图像处理领域被广泛应用[3-6]. 基于二阶偏微分方程的PM降噪模型是对热传导模型的优化具有良好的保边去噪性能， 但是当同样是高频信息的噪声点的梯度模值与边缘的梯度模值相似时， PM模型就会把噪声信息误判为边缘信息在该噪声点处减少扩散强度， 在图像演化过程中形成伪边缘(即“阶梯效应”). “阶梯效应”现象对所获降噪图像的主观视觉评价造成负面影响， 也对进一步的图像理解和图像分析造成不可估量的困难.

减少“阶梯效应”现象的一个有效途径是增加扩散模型中导数的阶数， 目前主要是基于四阶偏微分的降噪模型[7-12]. You和Kaveh两人首次提出了基于拉普拉斯算子的四阶偏微分方程降噪模型(YK模型)[10]， 通过分段斜面来逼近原图,有效地克服了“阶梯效应”. 但是YK模型不具有边缘保持特性， 而且很容易产生斑点噪声. 为了进一步优化YK模型， Mohammad Reza Hajiaboli将梯度模值引入YK 模型提出一种具有边缘保持能力的改进YK模型(MRHA模型)[11]， 该模型收敛速度相比YK模型有了很大的提升,并且在去除噪声的同时起到保持斜坡边缘(ramp edge)的作用， 但也有不足之处， 降噪图像的阶跃边缘(step edge)仍会失真. 此后， Mohammad Reza Hajiaboli基于局部几何特征对MRHA模型进行了进一步的研究， 提出了各向异性扩散四阶去噪模型(MRHB模型)[12]， 所提出的MRHB模型考虑了扩散的方向性， 可以更好地保留图像的边缘细节信息， 但在平坦区域引入“阶梯效应”影响了降噪图像的视觉效果.

在MRHB模型的基础上， 结合结构张量， 本文提出一种新的各向异性四阶偏微分降噪模型. 在图像平坦区域， 梯度和边缘方向具有同等强度的扩散， 而在图像边缘处， 只沿边缘方向进行扩散， 从而可以有效去除边缘噪声同时可以保留图像边缘细节. 此外， 在图像的角点处不进行扩散， 图像的角型区域得到有效保护.

1 四阶偏微分模型

1.1 各向同性四阶偏微分模型

为了有效去除二阶偏微分方程中出现的“阶梯效应”， You和Kaveh两人将拉普拉斯算子和高阶微分代入图像的能量泛函， 提出基于高阶偏微分方程的去噪模型[10]. 该模型的最小能量泛函为

f′(·)≥0.(2)

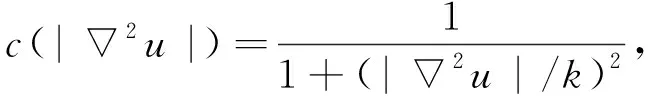
式中：k>0是拉普拉斯阈值. 阈值k的选择是影响去噪效果的关键参数之一.k值选择过小时， 噪声去除不彻底；k值选择过大时， 低对比度的边缘或纹理会被过度平滑掉.

YK模型利用分段斜面来逼近原图的,有效地克服了“阶梯效应”， 但是从图像的局部几何特征来分析该模型的扩散行为， 可知该模型实质上是各向同性的， 不具有保边能力. 具体原因阐述如下：

式中：η和ξ分别表示梯度方向和边缘方向，uηη和uξξ分别是图像沿着梯度方向和边缘方向的二阶方向导数. 显而易见， 在边缘方向和梯度方向的扩散强度是一样的， 所以该模型会导致图像中的边缘过度平滑， 使图像丢失边缘细节信息. 另外， 在去噪过程中会在结果图中产生一些孤立的黑白斑点噪声， 影响降噪图像的视觉效果.

Mohammad Reza Hajiaboli对YK模型进行了优化， 引入梯度模值作为YK模型的边缘检测算子提出一种改进的YK模型[11]

c(|u|)(7)

1.2 各向异性四阶偏微分模型

为了克服各向同性四阶偏微分去噪模型缺点， Mohammad Reza Hajiaboli提出了一种基于定向扩散的各向异性扩散四阶去噪模型[12]

c(|u|)(9)

式中：c1=c(|u|)2,c2=c(|u|). 因为函数c(·)恒小于1， 取值范围是(0，1]， 所以c1≤c2. 该模型以局部几何结构特征来刻画所执行的平滑过程. 平滑策略为主要沿着边缘方向进行扩散， 在梯度方向的扩散总体小于边缘方向， 以达到边缘保持的目的. 但这样的平滑机制使模型在平坦区域内边缘方向和梯度方向的扩散强度不同， 从而引入了“阶梯效应”影响了降噪图像的视觉效果.

2 基于结构张量的各向异性四阶偏微分模型

在图像处理中， 灰度图像的每一个像素除了具有灰度信息外， 还具有几何结构信息. 结构张量常用来分析与提取图像的局部信息， 如几何结构与方向. 结构张量已被广泛应用于数字图像处理和机器视觉领域[13]. 在图像处理中， 结构张量定义如下

Tρ(uσ

式中：Gρ表示以ρ为参数的高斯平滑核，ρ决定结构分析邻域的大小； *是卷积操作符；uσ表示对图像进行参数为σ的高斯平滑， 其使得边缘检测对于尺度小于的图像内容不敏感， 主要用来减少噪声对滤波的影响. 结构张量是一个对称的半正定矩阵， 其包含了比梯度模值更丰富的结构信息.Tρ的两个特征值分别为

(11)

它们对应的两个单位特征向量分别为

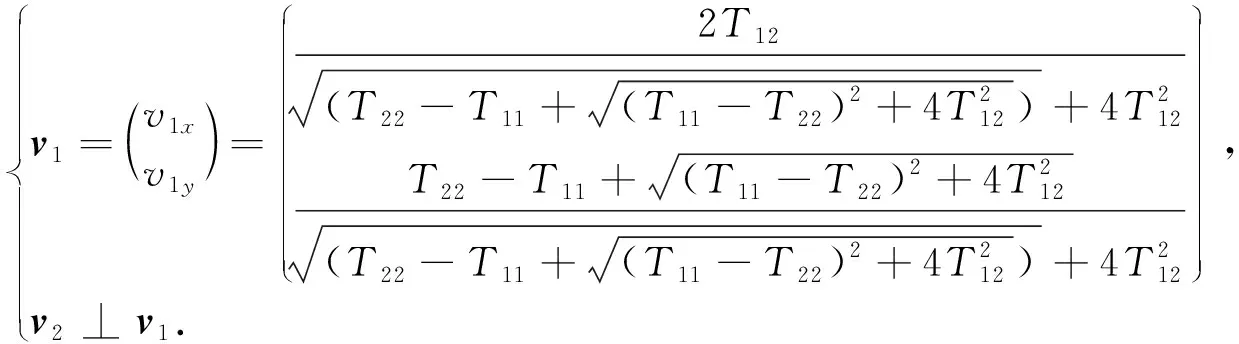
特征值λ1,λ2可以反映图像的局部结构特征， 在图像平坦区域，λ1≈λ2≃0； 在边缘区域，λ1≫λ2=0； 在角点区域，λ1≥λ2≫0. 特征向量v1,v2分别是对局部结构梯度和边缘方向的估计. 计算结构张量的迹h1(h1=λ1+λ2)和行列式h2(h2=λ1*λ2)， 通过区分h1和h2的关系可以区分图像的区域. 当h1≃0且h2≃0时， 像素分布在图像的平坦区域； 当h1≫0且h2≃0时， 像素分布在图像的边缘区域； 当h1≫0且h2≫0时， 像素分布在图像的角点区域.

受文献[14]启发， 利用图像的结构张量的行列式和迹作为边缘检测因子， 并且利用结构张量矩阵的特征向量来估计边缘和梯度方向， 同时为了更好地保持图像的细节， 引入数据保真项. 对新提出的数据保真项中的噪声图像用高斯滤波进行了预处理， 降低噪声点的梯度， 从而可以更真实地刻画噪声图像的几何结构特征. 本文提出如下基于结构张量的自适应四阶偏微分模型

(13)

式中：u0表示噪声图像；K是边缘保持阈值；λ为拉格朗日乘子， 对扩散项和数据保真项起到平衡作用；uv1v1和uv2v2分别是图像沿着由结构张量估计的梯度方向和边缘方向的二阶方向导数， 计算如下

(14)

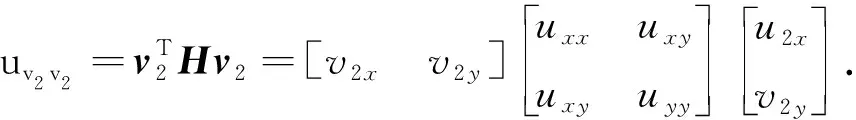
式(14)， (15)中H是海森矩阵. 由式(13)可知， 本文提出的模型关于图像梯度方向和边缘方向的扩散系数c1,c2分别取决于图像结构张量的迹和行列式. 在图像的平坦区域，h1≃0，h2≃0， 此时c1→1，c2→1， 则在梯度方向和边缘方向的扩散强度相同， 对图像进行各向同性扩散， 可以有效地去除噪声； 在图像的边缘区域，h1≫0，h2≃0， 此时c1→0，c2→1， 则只沿着边缘方向进行扩散， 可以有效保持边缘等细节； 在图像的平坦区域，h1≫0，h2≫0， 此时c1→0，c2→0， 则在梯度方向和边缘方向均不进行扩散， 可以有效地保护角点信息. 此外， 数据保真项的引入， 也使该模型可更好地保护图像的局部细节.

二、悄悄走过去，独自把丁主任抓个现行，给他警告，让他改过自新。这样也好，丁主任的工作和地位保住了，名声也保住了，我都一大把岁数了，就这样不明不白地背个名声也就算啦，再说也没什么人指名道姓地说小偷就是我。哎！还是多担待点吧，小丁走到现在也不易。

3 数值实现

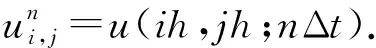
(16)

由此计算图像沿着由结构张量估计的梯度方向和边缘方向的二阶导数分别是

(17)

令g=c1uv1v1+c2uv2v2， 改进模型的离散形式可写为

(19)

对式(19)引入空间离散符号， 则

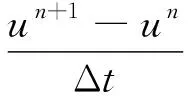
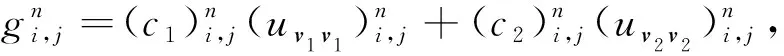
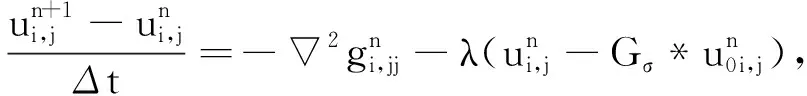
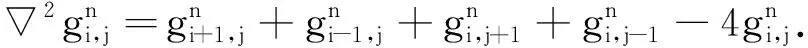
最后得到改进模型的下述离散的迭代形式

(24)

4 实验结果与分析

为了验证改进模型去噪的有效性， 本文进行了大量仿真实验. 在仿真实验中， 采用大小为256×256的Lena、 Boat和Peppers的标准图像作为测试图像， 对测试图像分别加入均值为0， 方差为0.002的高斯噪声. 分别用YK 模型[10]、 MRHA模型[11]、 MRHB模型[12]、 张量PM模型[14]、 张量自蛇模型[15]和本文改进模型对加噪图像进行滤波处理. 对其滤波性能采用主观评价(视觉效果)和客观评价来对去噪图像质量进行评价分析. 其中客观评价指标采用信噪比(SNR)、 均方误差(MAE)、 峰值信噪比(PSNR)， 其定义如下

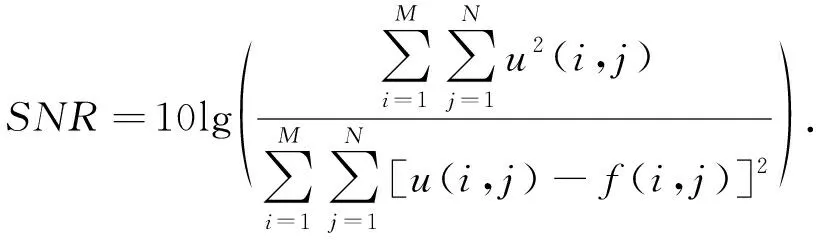
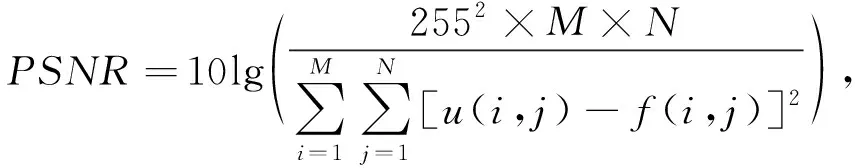
式中：M×N表示图像的大小，u和f分别表示原始图像和恢复图像.SNR值、PSNR值越大，MAE值越小表示图像去噪效果越好.

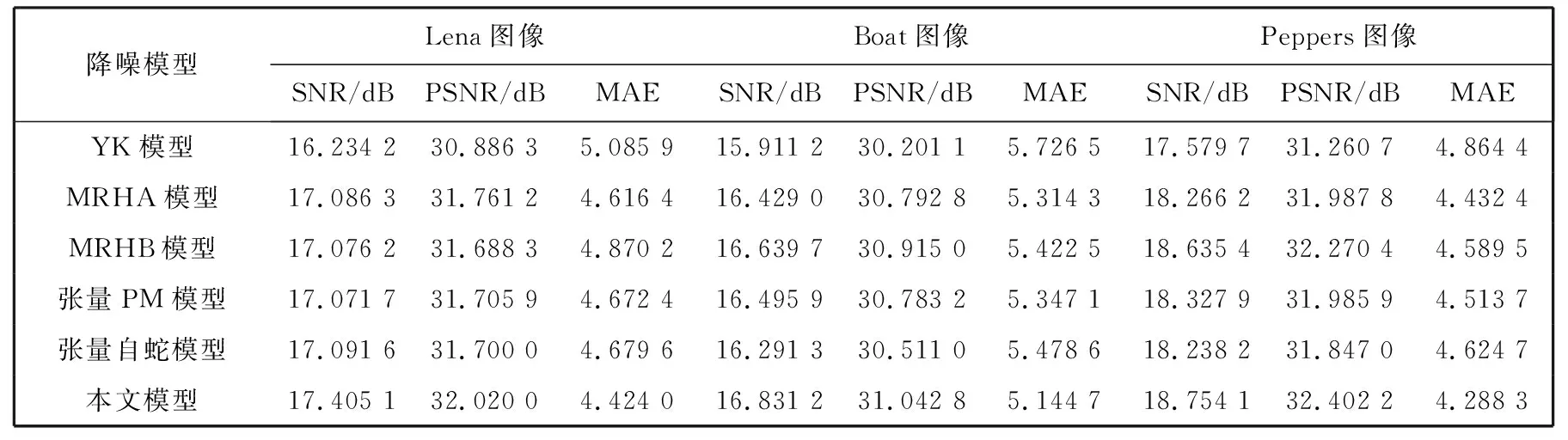
上述各模型的参数按最优实验结果进行设置. 经实验验证， 当时间步长Δt为0.05， 阈值参数K为60， 保真项系数λ为0.08， 迭代次数n为30时， 本文模型去噪效果最好. 滤波处理后图像的主观视觉效果如图 1～图 3 所示， 各种模型对应的客观评价性能指标比较如表 1 所示.

从图 1～图 3 可看出, YK模型的处理结果中边缘细节模糊， 会有一些孤立的黑白斑点的产生； MRHA模型的处理结果中黑白斑点得到有效的去除， 但是在边缘处仍有残留噪声， 边缘细节损失也较严重； MRHB模型的处理结果中边缘细节得到较好的保护， 但是会产生阶梯伪影带来不好的视觉效果； 张量PM模型的处理结果中图像的轮廓边缘失真严重； 张量自蛇模型的处理结果中在平坦区域产生了许多伪影； 而本文模型的处理结果具有较好的视觉效果， 图像噪声得到了有效的抑制， 边缘细节也得到了很好的保留， 如Lena图像的眼部和唇部等细节特征、 Boat图像中众多细微的线条轮廓和Peppers图像的边缘细节特征等. 从表1的客观评价标准可以看出， 在同等噪声条件下， 本文模型得到的信噪比、 峰值信噪比、 均方误差明显都优于YK 模型、 MRHA模型、 MRHB模型、 张量PM模型和张量自蛇模型. 因此， 本文所提出的模型比YK 模型、 MRHA模型、 MRHB模型、 张量PM模型和张量自蛇模型有更强的去噪效果和边缘细节保护能力.

图 1 Lena图像去噪效果对比Fig.1 Comparison of denoising results on Lena image

图 2 Boat图像去噪效果对比Fig.2 Comparison of denoising results on Boat image

图 3 Peppers图像去噪效果对比Fig.3 Comparison of denoising results on Peppers image

降噪模型Lena图像Boat图像Peppers图像SNR/dBPSNR/dBMAESNR/dBPSNR/dBMAESNR/dBPSNR/dBMAEYK模型16.234 230.886 35.085 915.911 230.201 15.726 517.579 731.260 74.864 4MRHA模型17.086 331.761 24.616 416.429 030.792 85.314 318.266 231.987 84.432 4MRHB模型17.076 231.688 34.870 216.639 730.915 05.422 518.635 432.270 44.589 5张量PM模型17.071 731.705 94.672 416.495 930.783 25.347 118.327 931.985 94.513 7张量自蛇模型17.091 631.700 04.679 616.291 330.511 05.478 618.238 231.847 04.624 7本文模型17.405 132.020 04.424 016.831 231.042 85.144 718.754 132.402 24.288 3

5 结束语

本文提出一种基于结构张量的各向异性四阶偏微分降噪模型， 该模型利用图像的局部几何信息， 根据图像结构张量的行列式和迹作为图像几何结构的边缘检测因子， 并依据图像结构张量的特征向量作为图像几何结构的方向信息， 自适应地在图像的边缘方向和梯度方向进行不同强度的扩散， 从而可以有效地去除噪声、 克服阶梯效应， 同时又能较好地保持图像的边缘细节. 与YK模型、 MRHA模型、 MRHB模型、 张量PM模型和张量自蛇模型相比表明， 该模型不仅具有更好的去噪效果， 而且具有更好的定向扩散能力和对图像的边缘细节特征的保护能力.