某坦克炮连续射击温升对身管变形影响

陈志坚， 宋大明， 徐宏英

(1. 解放军边防学院， 陕西 西安 710108； 2. 西安现代控制技术研究所， 陕西 西安 710065；3. 西北机电工程研究所， 陕西 咸阳 712099)

0 引 言

坦克炮在战争中发挥着重要作用[1]. 某105 mm 坦克炮在连续射击[2-3]过程中， 身管在变化的温度场[4-8]作用下发生复杂变形[9-13]， 严重影响了射击精度[14-15]. 因此， 迫切需要对温度场作用下该型号坦克炮连续射击过程中身管变形规律进行研究.

在研究过程中， 本文主要对以下两种工况进行了分析. 工况一为常温加自重作用下身管装配到位时保持平直无弯曲， 即炮口角0°， 15连发射击(3组5连发)； 工况二为常温加自重作用下身管装配到位时炮口端面向上旋转3′， 即炮口角3′， 15连发射击(3组5连发).

通过对比两种工况条件下的分析结果， 获得该型号坦克炮连续射击过程中初始炮口角及连续发射数目对身管变形的影响规律.

1 坦克炮身管变形分析模型

1.1 部件材料参数

坦克炮起落部分结构材料为某型号合金钢. 室温环境下， 其材料密度、 泊松比及热膨胀系数如表 1 所示， 弹性模量与温度的对应关系如表 2 所示. 坦克炮射击过程中， 周围环境温度取285 K.

表 1 某型号合金钢材料参数

表 2 某型号合金钢弹性模量随温度的变化

1.2 起落部分装配模型简化及网格划分

根据坦克炮起落部分结构特点、 分析目的及各部件实际装配关系对其进行简化. 模型简化时， 不考虑高低机的影响， 但考虑后坐部分与摇架的接触关系， 最终简化模型由身管、 抽气装置、 炮尾和摇架等部分组成， 有限元分析模型如图 1 所示.

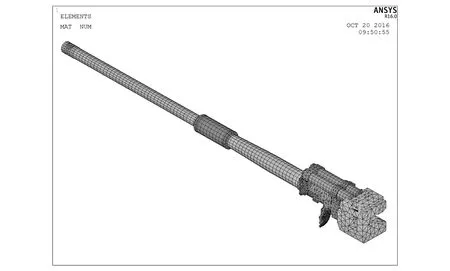
图 1 有限元分析模型Fig.1 Finite element analysis model

1.3 边界条件及载荷

根据实际情况， 对坦克炮起落部分装配结构施加相应的边界条件及载荷. 载荷主要为结构自重和身管内、 外壁随时间与空间位置变化的温度场载荷. 图 2 示出了第一组5连发射击过程中身管内、 外壁距身管尾部端面0.01 m(身管尾部附近)， 2.70 m(身管中间附近)， 5.10 m(炮口附近)处的温度-时间历程曲线， 第二、 三组5连发射击过程中温度-时间历程曲线变化规律同第一组基本相同.

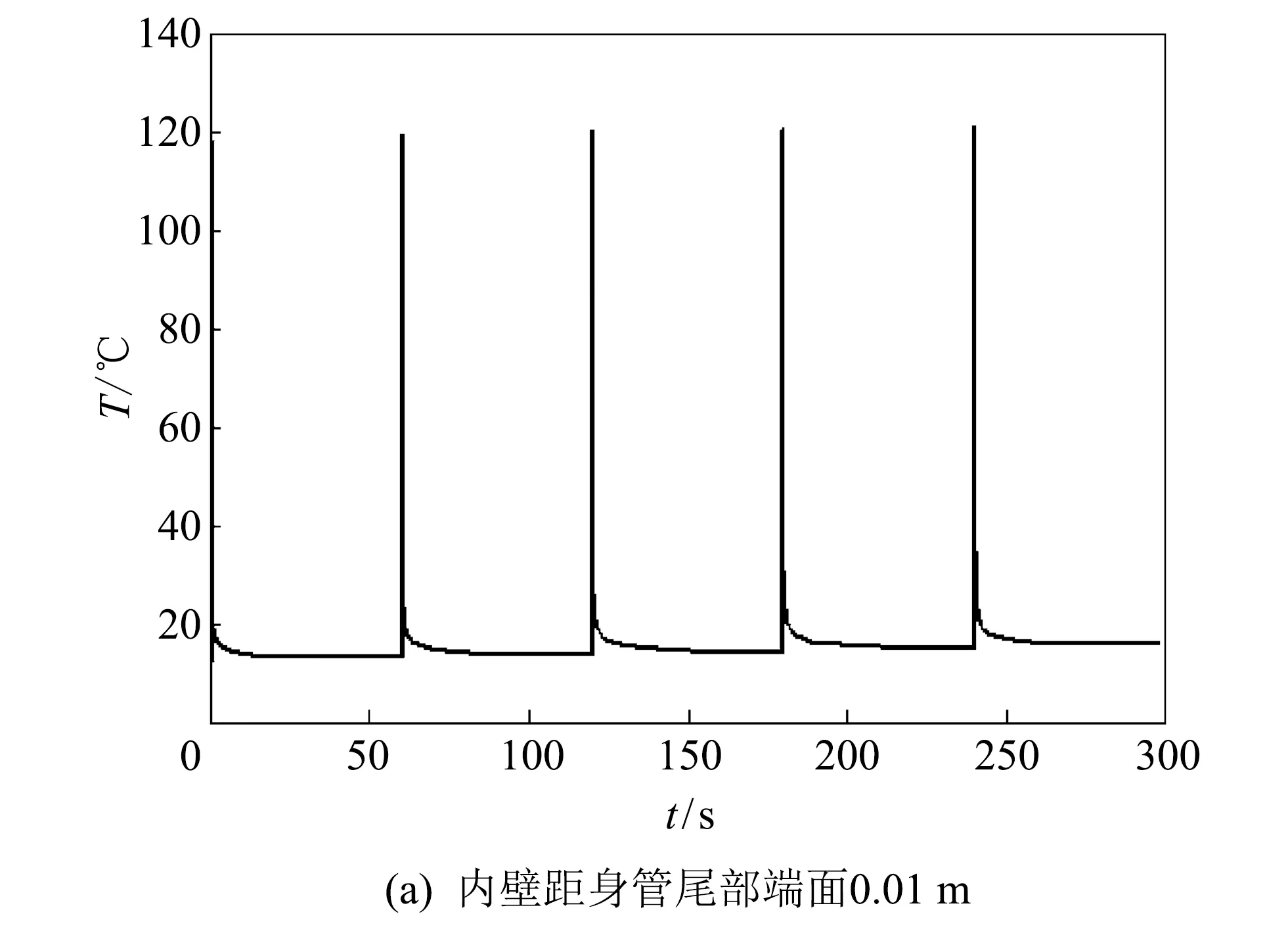
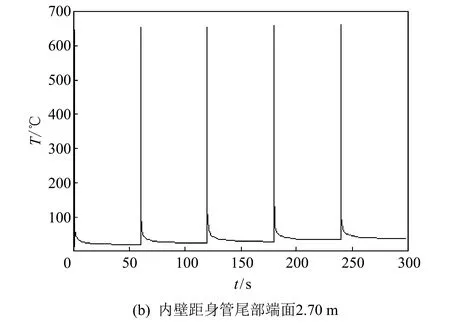
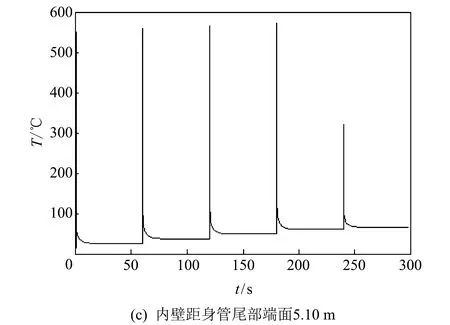
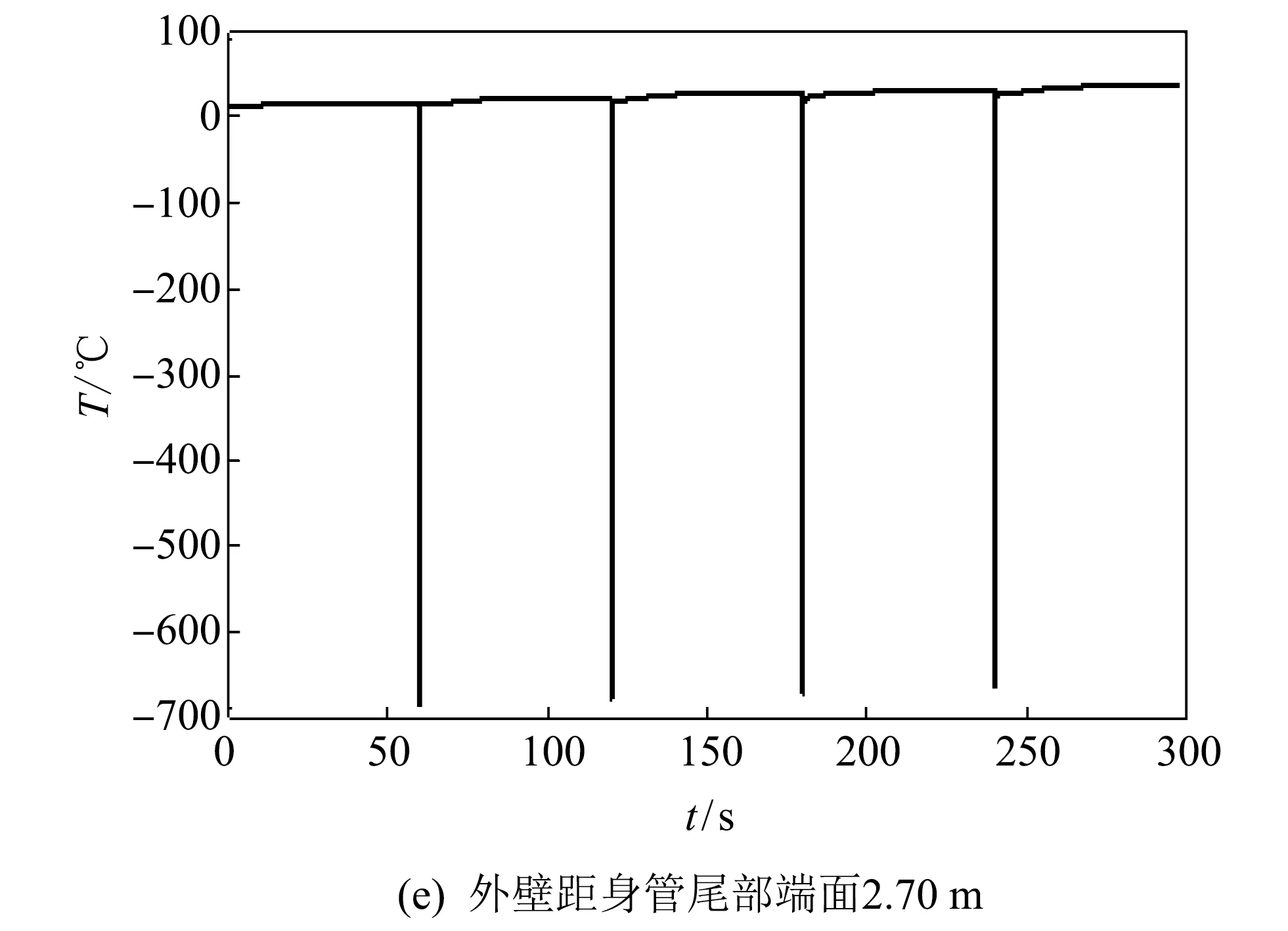
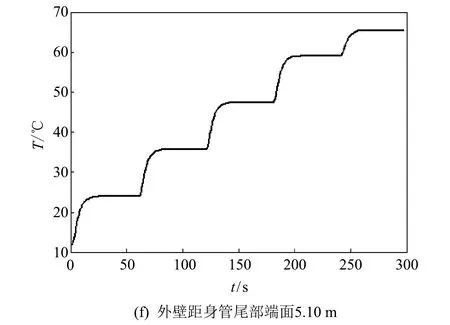
图 2 内外壁温度-时间历程曲线

在身管温度场分析过程中， 首先建立了膛内运动及后效时期火药燃气的温度方程， 然后分析并确定了内弹道时期身管膛壁对流换热系数， 随后建立了身管的传热学模型， 最后通过求解传热学模型获得了连发射击过程中身管不同位置处的温度-时间历程曲线[16]. 在同身管关键位置的温度试验测试值比较后， 确认最终获得的温度-时间历程是比较可靠的.

2 不同工况条件下坦克炮身管变形分析结果

对于坦克炮身管变形分析的两种工况， 每种工况的分析过程完全相同， 均分两步进行：首先进行整体结构自重作用下的常温静平衡状态计算， 然后施加随时间与位置变化的温度场载荷， 进行瞬态热-结构直接耦合分析.

在工况一(炮口角为0°)和工况二(炮口角为3′)条件下， 连续射击15发， 即三组5连发， 每组5连发中每发间隔1 min， 第一组5连发与第二组5连发时间间隔25 min， 第二组5连发与第三组5连发时间间隔20 min. 对于每一组5连发来说， 射击开始时刻和结束时刻分别指第1发击发时刻和第5发击发后60 s的时刻. 炮口中心高低方向和轴向位移随时间变化曲线如图 3 和图 4 所示， 炮口端面相对于初始炮口角高低方向的旋转角度(以下简称为炮口端面高低转角)随时间变化曲线如图 5 所示.

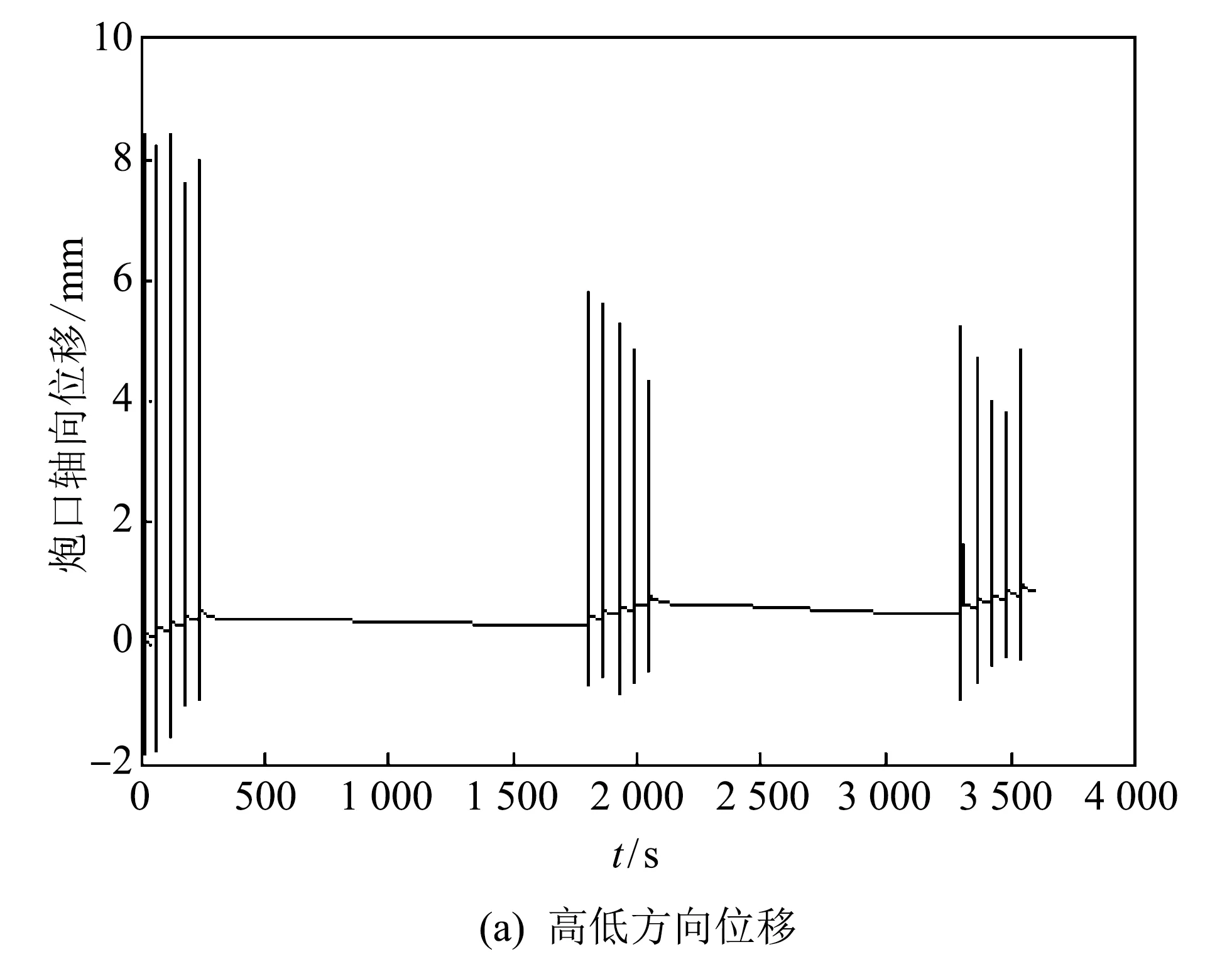
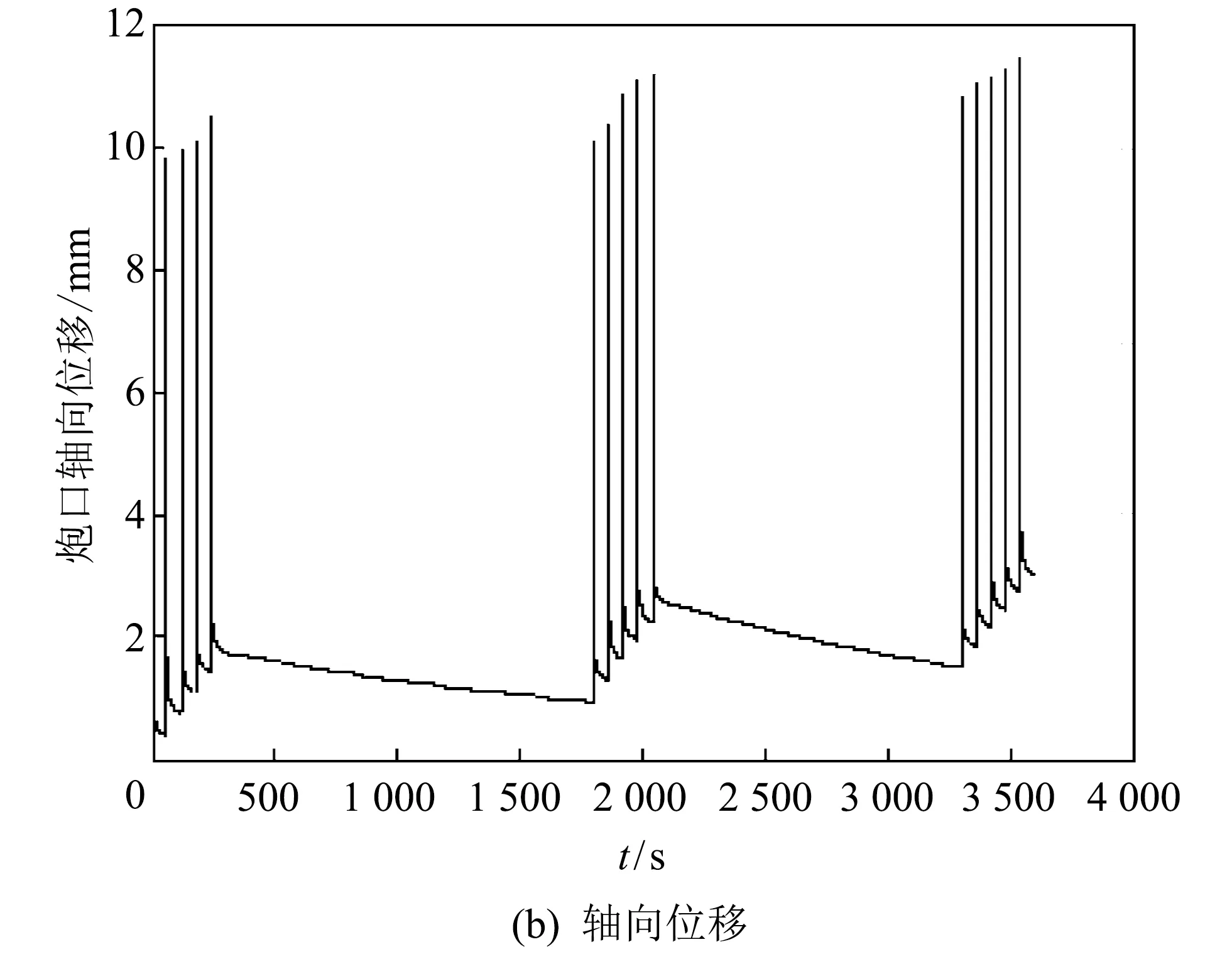
图 3 工况一条件下炮口中心位移随时间变化曲线Fig.3 Curves of displacement of gun muzzle center with time under condition one

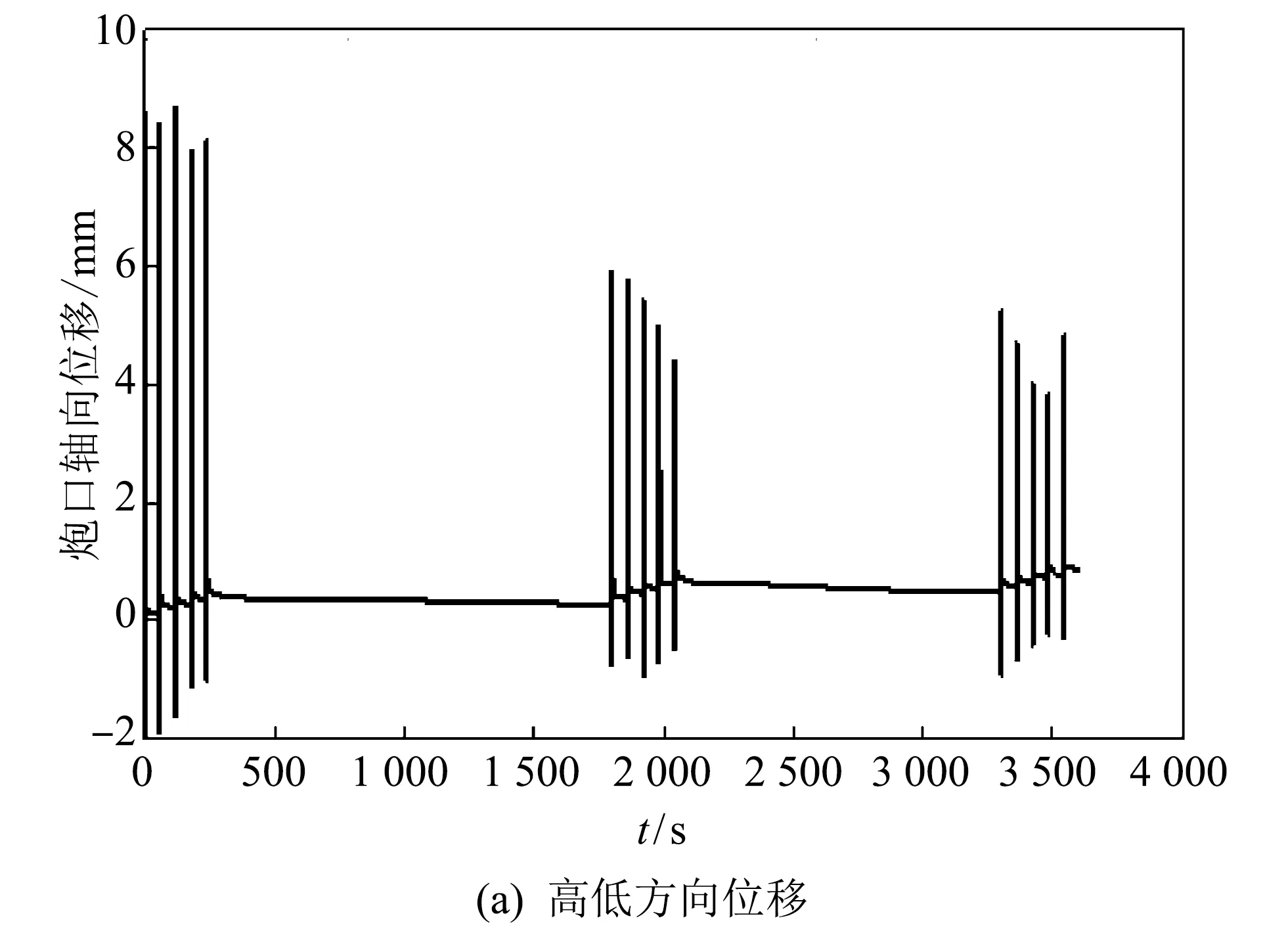
由图 3～图 5 可知， 每组5连发射击结束时刻， 炮口中心高低方向和轴向位移及炮口端面高低转角均比射击开始时刻大. 与上一组5连发结果相比， 下一组5连发， 炮口中心高低方向位移的幅值变小， 轴向位移的均值变大.

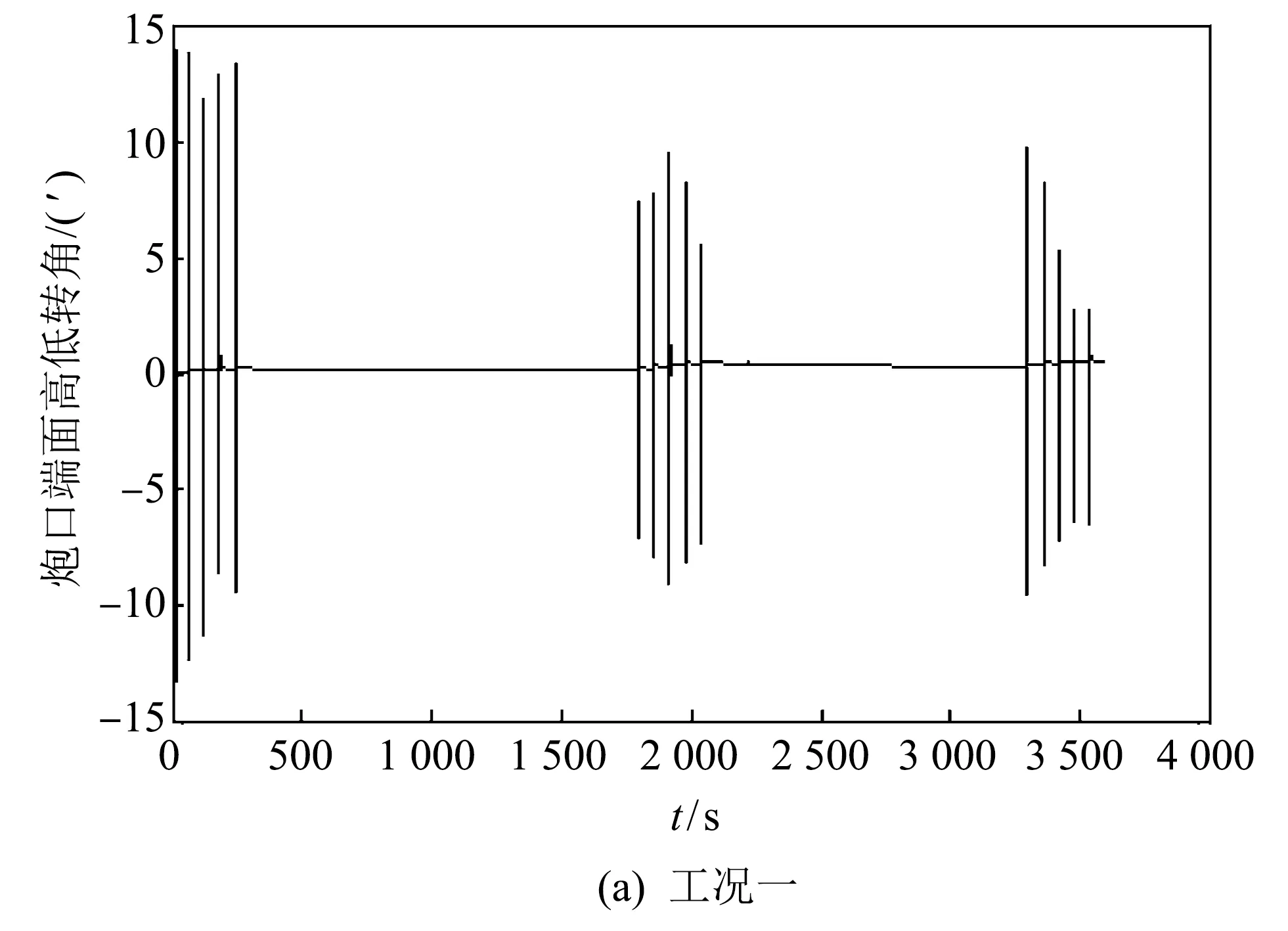
图 5 炮口端面高低转角随时间变化曲线Fig.5 Curves of high-low rotation angle of face of gun muzzle with time

0°和3′两种初始炮口角度条件下， 15连发射击过程中， 每组5连发结束时刻， 炮口中心的高低方向和轴向位移如表 3 所示， 每组5连发开始及结束时刻炮口端面高低转角数值如表 4 所示.

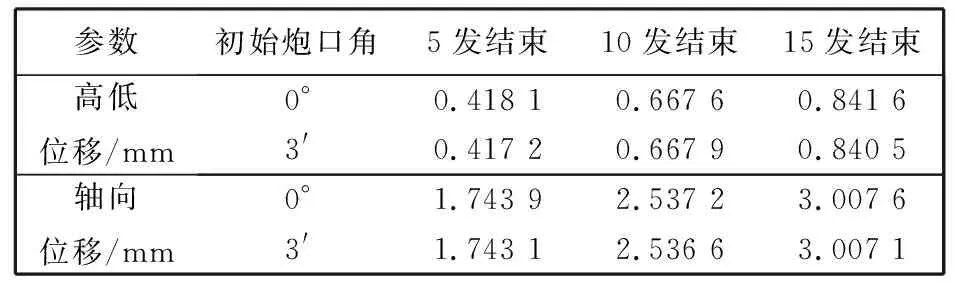
表 3 不同初始炮口角条件下的炮口响应结果

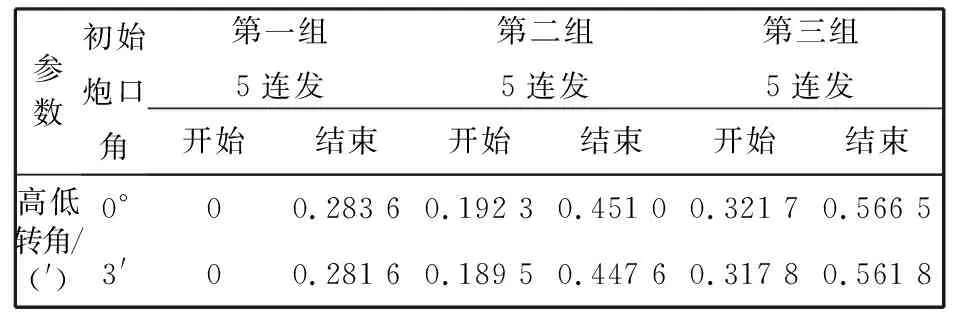
表 4 炮口端面高低方向转角

由表 3 可知， 初始炮口角分别为0°和3′两种角度下， 5发、 10发和15发射击结束时刻炮口高低方向和轴向位移均相差很小， 高低方向位移分别约为0.42, 0.67和0.84 mm， 轴向位移分别约为1.74, 2.54, 3.00 mm.

由表 4 可知， 初始炮口角分别为0°和3′两种角度下， 5发、 10发和15发射击结束时刻炮口端面高低转角相差很小， 分别约为0.28′, 0.45′和0.56′.

图 6(a)～(f)给出了工况一在0.008, 300, 1 800, 2 100, 3 300和3 600 s时刻身管的高低方向变形图.

图 6 工况一条件下各时刻身管高低方向变形云图

图 6 所示的高低方向最大位移， 0.008 s时刻比300 s时刻大得多， 因为击发后极短的时间内身管内壁温度更高， 温度场更复杂； 1 800 s时刻和3 300 s时刻分别比300 s时刻和2 100 s时刻小得多， 因为从前一组5连发结束时刻至下一组5连发开始时刻， 身管内外壁温度逐渐降低， 身管又慢慢向下弯曲.

3 结 论

笔者以某105 mm坦克炮起落部分为研究对象， 建立了坦克炮身管变形分析有限元模型， 在温度场作用下， 进行了连续射击过程中两种工况条件下的动态响应特性分析， 获得如下规律：

1) 随着射击发数增加， 身管温度也随之升高， 身管材料弹性模量随温度升高而降低， 在结构自重与温度场共同作用下炮口高低方向与轴向变形也在增加.

2) 初始炮口角分别为0°和3′两种角度下， 多重因素综合作用下的身管炮口高低方向与轴向变形相差很小.

3) 初始炮口角分别为0°和3′两种角度下， 相同射击发数结束时刻的炮口端面高低转角相差很小， 且随着射击发数增加， 炮口端面高低转角持续增大.

4) 对每组5连发来说， 射击结束时刻相对于开始时刻身管在多重综合作用下炮口向上翘起； 而从前一组5连发结束时刻至下一组5连发开始时刻之间的时间段内， 随温度下降身管又向下弯曲； 但整体来看， 随着射击组数的增加， 炮口端面高低转角也随之增大.