机床箱体有限元分析与轻量化设计
张焕梅, 郭芸俊
(1. 太原工业学院 机械工程系, 山西 太原 030008; 2.太原工业学院 计算机工程系, 山西 太原 030008)
0 引 言
传统的机床箱体作为机床总成的主要承载部件, 其受力情况比较复杂, 会受到较大的弯曲、 扭转力的共同作用. 若箱体的强度、 刚度不够, 就很难满足机床工作时的稳定性要求; 若仅为了保证总体强度而单纯增加箱体厚度, 则机床的总重量就会增大, 增加了制造成本. 因此在满足强度、 刚度及使用要求的条件下, 设计出体积最小或质量最轻的机床箱体结构就显得非常关键[1-2].
随着有限元分析理论与现代优化技术的发展, 企业在产品研发、 升级过程中逐步开始普及应用新技术. 有限元法(Finite Element Method)[3]是分析机床结构应力应变分布的有效方法之一, 既可以检验机床箱体结构的强度是否满足要求, 也可以进行结构优化.
目前集有限元分析和结构优化设计的商业优化软件(如ANSYS, Hyperworks,OptiStruct等)也在机床界逐步普及, 优化技术在工业上的应用逐渐展开[4-5]. 例如Altintas和Cao[6]以机床主轴系统为研究对象, 建立了具有非线性特征的主轴与轴承有限元模型, 并通过试验数据与有限元分析对比, 验证了该有限元建模方法的可行性, 同时为机床结构动态分析和优化设计提供了指导. 文桂林等[7]在高速机床零部件优化设计研究中, 以结构尺寸为设计变量, 提出了基于近似模型的机床零部件优化设计方法, 有效提高了机床零部件设计的效率, 为其结构改进提供了理论依据, 降低了生产成本.
本文以机床的床头箱为研究对象, 基于不同加载方式对有限元结果的影响, 对模型进行有效简化, 获得精度较高的有限元模型. 同时为提高优化计算效率, 通过灵敏度分析方法得出床头箱壁厚对于质量、 位移及应力的影响, 分析后筛选出合适的因素, 最后根据结构优化设计理念, 以轻量化为目标建立数学模型, 采用尺寸优化方法进行迭代计算, 获得有效的最优解.
1 机床床头箱有限元建模与分析
1.1 机床床头箱三维模型的建立
床头箱是机床的一个重要部件, 如图 1 所示, 床头箱由壳体、 主轴及其轴承、 工件传动装置组成, 根据其工作原理, 本文选择了顶尖装夹的方式, 故主轴不转动, 所以带轮和电机模型不需要绘制, 利用三维软件绘制机床床头箱零部件模型数据并进行装配.
如图 1 所示床头箱中壳体模型, 顶部的空缺设计是为了表示电机位置和垫板形状, 两侧面有多个定位孔, 底板有螺钉孔, 底部有和底座连接的孔和定位孔; 内部心轴由轴套、 主轴和顶针组成, 顶针尾部为锥形嵌入主轴的锥孔中, 主轴、 轴套、 心轴是无间隙装配.
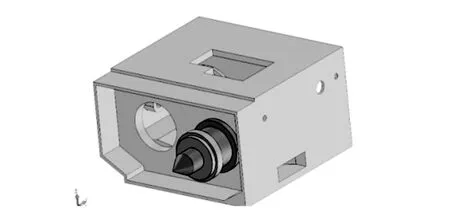
图 1 床头箱总装配模型Fig.1 The machine tool headstock assembly model
1.2 机床床头箱有限元模型的建立与分析
床头箱结构由于加工定位、 工装等条件约束, 侧板上的定位孔、 连接孔等让床头箱箱体比较复杂, 但这些孔位对机床床头箱的力学性能及本文轻量化的研究影响不大, 反而增加了有限元网格的划分难度, 所以在进行有限元建模前先对机床床头箱结构进行模型简化[8], 其三维模型简化过程如下:
1) 将壳体两侧与底端的定位孔、 螺栓孔等进行简化, 定位孔是加工和安装时辅助定位的, 对床头箱结构性能无影响; 底板与底座螺栓孔起到固定床头箱的作用, 在有限元建模过程中通过虚拟约束体现.
2) 将壳体的部分倒角和凸台简化, 本文选用顶尖装夹, 主轴不转动, 故内部的变速传动结构可进行简化; 倒角和凸台属于工艺, 故可简化.
3) 顶部电机的位置孔是为了说明电机的位置和电机垫板的形状, 在有限元建模中通过不同加载方式来模拟电机负重.
其中简化过程与结果如图 2 所示.

图 2 三维模型简化过程与结果Fig.2 Result and process of model simplification
在有限元分析软件Hyperworks中导入模型, 划分网格, 壳体抽取中心面, 划分成2D壳单元网格, 其单个壳单元尺寸为3 cm ×3 cm; 在对主轴划分网格时, 选用的单元类型为二阶实体四面体单元, 每个二阶四面体单元有10个节点(4个角点和6个中间节点), 并且每个节点有3个自由度. 二阶实体四面体单元模拟了二阶(抛物线型)位移场以及相应的一阶应力场, 当单元因加载而变形时可有效地传递载荷. 在壳体和主轴之间定义3D-2D接触关系来传递载荷关系, 最终完成有限元模型, 如图 3 所示.

图 3 机床床头箱有限元模型Fig.3 Finite element model of machine tool headstock
床头箱结构的主要作用是固定于保持工件的作用, 在工作过程中主要受压、 弯、 扭三种形式的组合变形. 根据金属切削原理[9-10], 查表得到工件为铸铁时沿工件径向进给方向的作用力Fx/Fy比值最大, 取值为3, 则水平方向的最大载荷Fx=3Fy=1 206 N; 机床砂轮主电机的功率为14.08 kW, 砂轮线速度为v=35 m/s, 由公式得切向力Fy=1 000P/v=402 N, 假设工件重力为G1=9 800 N, 则竖直向下的载荷为FG=9 800 N+402 N=10 202 N; 径向切削力与水平惯性力同时作用在被夹持工件上, 假设加工过程中床头箱和尾架顶尖的距离为1 000 mm, 在工件的中心位置到顶尖前端的节点产生一个扭矩M=743×500=3.72×105N·mm; 最后床头箱顶部电机重70 kg, 垫板重2 kg, 重力载荷为G2=705.6 N, 电机和砂轮的质量偏心产生惯性力为100 N.
如图 4 所示为力的加载示意图, 顶尖处切削产生的竖直载荷FG=10 202 N, 水平载荷Fx=1 206 N, 扭矩M=3.72×105N·mm, 床头箱电机的重力G=705.6 N, 惯性力F3=100 N; 整个底面约束Z方向自由度, 2个螺钉孔处约束6个自由度.
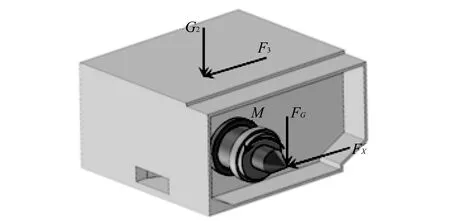
图 4 机床床头箱结构受力图Fig.4 Machine tool headstock structure diagram
床头箱材料的基本参数: 铸铁材料的密度为7 200 kg/m3, 泊松比为0.25, 弹性模量(E)为1.2×105MPa.
根据力学分析, 其载荷对机床床头箱的影响主要在主轴顶尖与靠近顶尖的壳体前板区域. 根据圣维南原理, 在弹性结构一块区域上的载荷所引起的应力, 在离载荷作用稍远的地方, 基本上等同于载荷的合力和合力矩. 本文研究的工况为静力学, 底面的6个自由度已经全部约束, 模拟电机的载荷相对较小, 而且加上底端自由度约束的影响, 其合力和合力矩对于主轴和壳体前板的应力影响几乎为零.
为了验证该分析的正确与否, 同时进一步简化优化仿真模型, 本次有限元分析中通过三种不同仿真加载方式将电机的力加载于壳体顶板, 同时增加一组电机载荷为零仿真分析作为对比, 三种方案有限元仿真模型如图 5 所示, 具体试验方案如下:
方案一: 床头箱电机的重力和惯性力通过一个等效节点, 等效节点与床头箱壳体之间通过刚性rigid连接来传递载荷;
方案二: 床头箱电机的重力和惯性力通过有限元网格间的节点, 将载荷均匀分布在该区域;
方案三: 床头箱电机的重力用压力的方式加载于安装区域, 根据压力公式P=F/S, 每个单元平均施加压力.

图 5 三种方案有限元仿真模型Fig.5 Finite element simulation models of three schemes
通过有限元分析软件Hyperworks进行静力分析, 在有限元模型中选择主轴顶尖处相同的节点提取位移量, 得出了床头箱的位移云图和应力云图, 三种方案的详细分析结果数据对比如表 1 所示.

表 1 三种方案仿真结果比较
通过分析结果对比, 虽然床头箱电机力的加载方式不同, 但床头箱的最大位移都集中在主轴顶尖处, 三种方案的位移量相差不大, 且最大应力的区域也相似, 均分布在床头箱前板与主轴轴套相配合的凸台上.
针对机床床头箱的静力分析中, 电机的重力和惯性力的合力对于主轴顶尖处的位移和壳体前板应力的影响很小, 符合前期的相关力学分析, 其中方案一是根据前期力学分析而提出的简化性方案, 有利于提高优化迭代的计算效率, 本文采用方案一的建模方式来进行优化分析计算.
2 机床床头箱结构优化设计
2.1 设计思路与流程
机床床头箱主要由箱体与主轴系统组成, 其中主轴系统是机床的核心件, 设计影响因素众多, 不适合作为本次优化的目标, 考虑到再设计及生产成本, 轻量化设计在尽量不改变模具、 工艺等情况下, 由板筋件组成的箱体外壳是最佳选择, 以有限元分析为基础, 通过优化箱体板材的厚度来达到减重的目的[11].
床头箱主轴系统的回转精度和刚度直接影响产品的质量, 根据机床设计手册机床主轴的回转精度为0.07 mm, 刚度不小于150 N/mm[12]. 根据前述有限元分析数据结果表明, 最大位移发生在床头箱顶尖处, 最大应力分布在壳体前面, 故在后续优化设计中要保证壳体满足许用应力, 同时主轴顶端处的最大位移不能大于限定值.
根据以上设计准则, 床头箱在静态工况下的轻量化设计流程如图 6 所示.

图 6 结构尺寸优化流程图Fig.6 Optimized flowchart of structural dimensions
2.2 灵敏度分析方法
机床床头箱箱体为壳体模型, 根据设计方案, 主要是对壳体的尺寸优化, 其初始壁厚的尺寸为: 前圈和后圈壁厚为10 mm, 顶板和底板壁厚为20 mm, 前板和后板的壁厚为25 mm, 左侧板和右侧板的壁厚为15 mm. 根据壁厚对性能的影响划分为8个设计变量, 如图 7 所示为X1前板、X2前圈、X3顶板、X4左侧板、X5后圈、X6右侧板、X7后板和X8底板.

图 7 壳体参数变量布局Fig.7 Shell parameter variable layout
在结构力学分析中, 定量研究目标函数、 约束函数对设计变量的敏感程度称为灵敏度分析[13-14]. 假设由多参数定义的目标函数为f(x1,x2,…,xn), 那么该函数f对各个参数的导数, 即被称作该参数对函数f的灵敏度, 其数学表达式为
(1)
式中:uj为第j个响应;xi为响应的第i个设计变量;X0为由设计变量的初始值组成的向量, 通过求解响应的灵敏度, 可以在设计变量的可行域内逐步逼近响应的最优化解[15].
针对大型复杂结构设计问题, 灵敏度分析可以看作是确定模型输出信息与模型输入信息变化的关键技术, 在建立模型、 检验模型、 鉴定模型等方面具有重要的作用, 主要体现在以下几个方面[16]:
1) 灵敏度分析可确定不同自变量对响应对象影响的重要程度, 从而减少有限元模型的校核次数, 提高效率;
2) 灵敏度分析可以确定输入信息的不确定性从而判断科学假设的真实性;
3) 灵敏度分析可以得到对输出信息影响较大的输入参数, 可以从模型中去除不重要的参数从而简化模型.
利用Hyperstudy软件, 基于正交试验设计进行灵敏度分析, 选择机床床头箱质量M、 床头箱主轴顶尖测点位移δ及应力σ为响应量, 获得机床床头箱的8个尺寸对以上3个响应量的灵敏度数据, 如表 2 所示.

表 2 尺寸变量对于不同响应的灵敏度仿真分析
为了能够直观获得自变量的尺寸变化对不同响应量的影响, 经过进一步统计处理, 可得到尺寸变化对该3个响应量的影响百分比, 如图 8 所示.

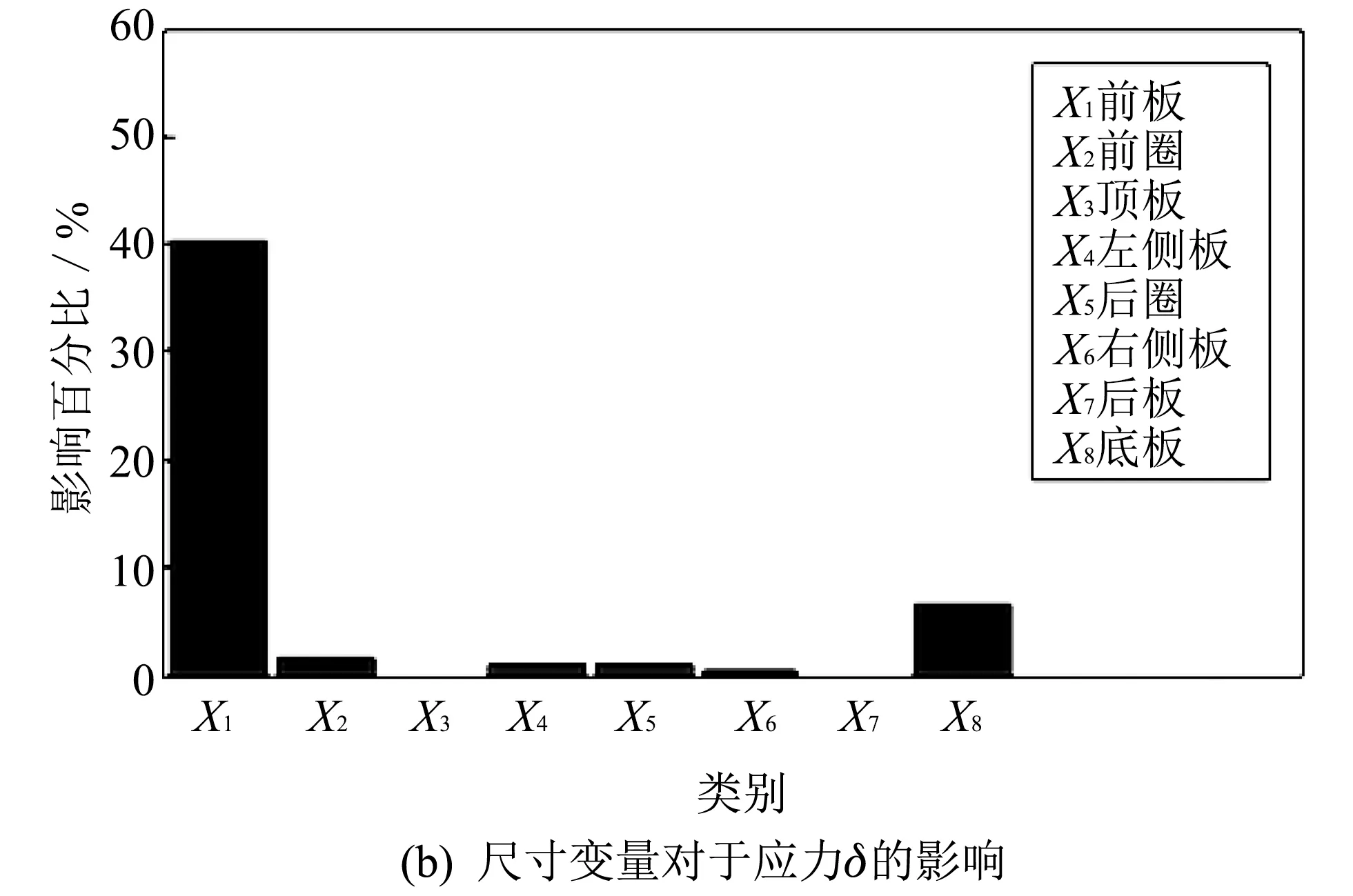

图 8 尺寸变量对于不同响应的影响百分率Fig.8 Size variables have a percentage effect on different responses
通过数据分析, 发现对于位移和应力的影响, 前板X1所占比重最高, 说明灵敏度比较高, 如果改动其值对于位移和应力的影响很大, 但是对于质量M的影响不是最主要的, 故不选择前板X1作为优化变量; 对于底板X8, 对质量响应的贡献度很小, 对位移和应力响应的贡献度比较高, 故也不选择其为优化设计变量. 顶板X3、 后圈X5和后板X7对质量的贡献度比较高, 对于位移和应力的贡献度比较小, 最终选择这三个因素进行优化.
2.3 优化数学模型的建立
基于轻量化的机床床头箱优化模型中, 以质量最小作为优化目标, 考虑到结构刚度能反映机床的整体性能, 故数学模型中以刚度作为其中一个重要约束. 结合床头箱的设计要求, 主轴的回转精度为0.07 mm, 床头箱壳体的材料为灰铸铁HT100, 是脆性材料, 以断裂为主要失效方式, 强度极限σb=100 MPa, 安全系数nb通常取2~3.5, 故床头箱的许用应力为[σ]≤50 MPa. 所以静态工况下机床床头箱优化的数学模型表示为
FindX=(x1,…,xi,…,xn)T,
MinimizeM,
s.t.δ(x)≤0.07 mm,
[σ]≤50 MPa,

在HyperWorks中对机床床头箱结构的箱体厚度进行尺寸优化, 结果7次优化迭代后, 位移达到约束值0.07 mm, 取得最优解, 停止迭代计算, 具体参数改变如表 3 所示.
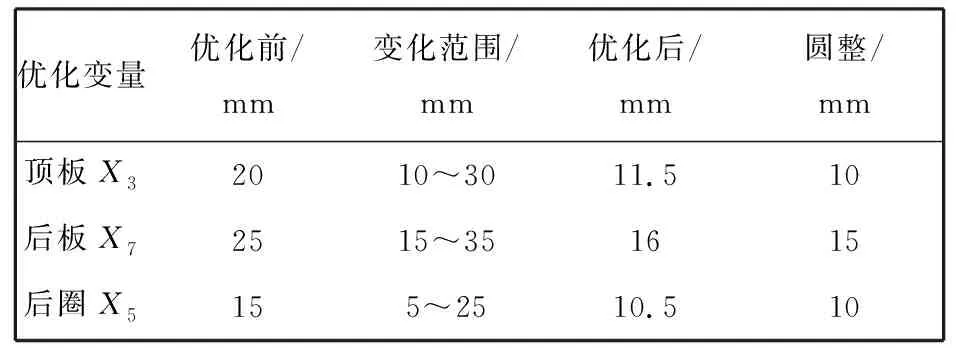
表 3 优化前与优化后的尺寸
将优化后的圆整结果更新到有限元模型中重新计算, 查看优化后床头箱的位移和应力情况. 如图 9 所示, 优化前机床床头箱结构的最大位移为62.9 μm, 优化后的最大位移为69.37 μm<δ=70 μm; 优化前的最大应力为46.748 MPa, 优化结构的最大应力为47.96 MPa<[σ]=50 MPa, 满足设计要求.
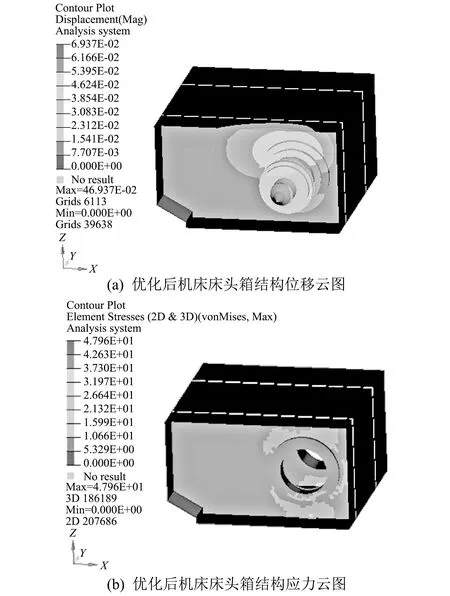
图 9 优化后机床床头箱有限元分析Fig.9 The finite element analysis of machine tool headstock was optimized
通过优化床头箱与原床头箱位移和应力云图的分析, 优化后的床头箱质量减小, 而且位移和应力满足设计要求. 优化后机床床头箱质量减重比达到18.33%, 其优化前后质量对比如表 4 所示.

表 4 优化前后结构质量比较
3 结 论
本文以机床床头箱结构为例, 提出了一种基于灵敏度分析的床头箱结构轻量化方法, 研究了有限元分析精度及计算效率的关键问题, 获得了有效的简化模型, 最后在轻量化目标下进行了尺寸优化设计, 获得可靠的最优解, 并通过优化前后对比表明, 在保证机床床头箱性能要求的前提下, 质量得到较大下降, 验证了提出的优化方法的可行性, 同时对机床结构进行全面优化研究具有一定的指导意义.

