高压输电线路覆冰清除爆破参数研究

谢东升， 宋 巍， 王 玮， 孙 滔， 黄铁铮， 蔡宣明

(1. 国网山西省电力公司经济技术研究院， 山西 太原 030051； 2. 中北大学 理学院， 山西 太原 030051)

电力为国民经济有条不紊的发展提供了有力的能源保证， 但是， 高压输电线覆冰的问题给高压输电线路带来了极大的安全隐患[1-4]， 严重影响到国家电网的稳定正常运行及人们的正常生活， 因此， 消除高压输电线路的覆冰隐患变得极为迫切.

高压输电线路除冰问题是当前国内外研究的热点和难点， 目前国内外研究报道的主要是传统除冰方式. 已有的各种直接应用于输电线上的除冰设备， 采用强力振动法、 滑轮铲刮法等相对较为简单的机械办法来处理覆冰(机械除冰法)， 其中的滑轮铲刮法比较实用， 它所消耗的能量较少， 而且价格便宜， 但其在使用过程中比较困难， 安全性不高[5]； 随后发展的很多机械除冰法， 如近些年较为热门的机器人除冰法， 除冰效果较好， 但是其能量消耗大， 还会受天气的影响； 总之， 机械除冰法不是一种非常理想的除冰方式， 其安全性差， 工作效率低[6]. 一些研究学者利用风及其他自然力的作用， 再应用辅助设备， 例如在高压输电线上安装平衡锤、 阻雪环等辅助设备， 使输电线上的覆冰达到一定程度时自动脱落， 从而起到防冰及除冰的作用(被动除冰法)， 此方法较为简单方便， 而且成本较低[7]， 但是， 其只实用于特定的时间和地点， 不能广泛地应用于所有输电线的覆冰情况， 该方法不能全面有效地消除输电线覆冰的危害. 另一些研究学者利用输电线路本身的发热以及一些附加的热源， 使得冰雪无法在输电线上覆冰， 或者使已形成覆冰的地方熔化， 从而达到除冰的效果(热力除冰法). 其中， 低居里铁磁材料应用较为广泛， 当温度小于0 ℃时， 这种材料磁滞损耗大， 产生的热量使得输电线表面不易形成覆冰， 或使得已经覆冰的地方熔化， 达到防冰、 除冰的效果； 当温度大于0 ℃时， 此时不需要熔冰， 该材料的磁滞损耗较小[8]. 热力除冰法效果较为明显， 但是消耗的能量大， 使用范围较小， 设备成本投资大， 不适宜远距离防冰及除冰. 除了上述除冰方法之外， 国内外也研究了电晕放电、 电子冻结、 碰撞前颗粒冻结以及超声技术等除冰方法. 但是， 电晕放电已被证明对除冰没有明显的效果， 电子冷冻只在负极性条件下才有用， 使用范围极小， 超声技术也已证明没有明显的除冰效果[9]. 综合国内外研究现状， 对高压输电线路除冰方式多集中在传统的方法上， 而对爆破除冰方式的研究很少.

本研究结合实验研究获得的冰与输电线路接触表面的摩擦系数， 以及相关文献参数， 应用LS-DYNA对高压输电线路爆破除冰进行模拟仿真计算， 计算控爆参数， 确定输电线路上炸药的最佳分布方式， 并通过缩比实验验证仿真计算结果.

1 高压输电线路覆冰的形式及机理

1.1 覆冰的形式

按照高压输电线路覆冰的形成及危害， 大致可以分为白霜、 积雪、 雾凇、 混合凇、 雨凇五种类型[9-12]， 这些覆冰的种类有以下几个特点：

空气中的湿气接触到0 ℃以下的冷物体时， 在其表面上就形成了白霜[13]， 虽然其对高压输电线的威胁不大， 但是输电线路的电晕损失会有所增加. 自然降雪(有干雪和湿雪)到高压输电线时， 就形成了积雪， 干雪密度≤0.1 g/cm3， 对输电线的黏附作用力很微弱； 湿雪密度约为0.103 g/cm3， 其对输电线的黏附作用力较弱. 雾凇的密度在0.1～0.3 g/cm3之间， 其对输电线的黏附作用力很弱. 混合凇的密度大约为0.507 g/cm3， 其较为坚硬， 对输电线路的黏附作用力较大. 雨凇的密度>0.8 g/cm3， 比较坚硬， 且对输电线路的黏附作用力非常强.

1.2 覆冰的机理分析

干增长和湿增长是分析高压输电线覆冰的形式及其机理的重要依据， 其实质是分析覆冰过程的热平衡及热传递. 输电线的覆冰密度、 厚度都取决于输电线表面的热平衡状态， 初始建立的输电线路覆冰的热平衡方程[14]为

Q0+Qf+Qr1=Qd1+Qd2+Qd3+Qr2,(1)

式中：Q0是空气摩擦对冰表面所加的热量；Qf是将冰从0 ℃降到覆冰表面的稳定温度时所释放的热量；Qr1是冷冻时所释放的能量；Qd1是在碰撞过程中过冷却水滴上升到0 ℃时所吸收的热能；Qd2是空气与输电线表面热对流所损失的热量；Qd3是冰面辐射时所损失的热量；Qr2是覆冰表面升华或蒸发时所消耗的能量. 式(1)的左边表示输电线路覆冰表面所吸收的能量， 右边表示损失的能量. 该初始热平衡方程能够初步揭示输电线路覆冰能量分配的基本形式， 但是该平衡方程忽视了覆冰湿增长过程中的碰撞水滴的动能、 热传导等对覆冰状态的影响， 而未考虑到输电线路的电流及其电场对覆冰状态的影响， 然而实际中这种影响还比较重要， 因此， 为了能够更好地揭示输电线路覆冰状态中的能量关系， 文献[9]建立了更加完善的热平衡方程

Q0+Qf+Qr1+Qb+Qc+Qd=

Qd1+Qd2+Qd3+Qr2+Qk+Ql+Qm,(2)

式中：Qb是日光短波加热；Qc是过冷却水碰撞冰面时动能所加的热；Qd是电流传输过程中的焦耳热；Qk是水滴离开冰面时所消耗的热能；Ql是在热传导过程中所损失的能量；Qm是风强制对流时的热损失.

2 爆破除冰数值模拟

基于LS-DYNA对爆破除冰进行仿真， 考虑到爆炸问题中结构的大变形和高应变率效应， 采用流固耦合方法计算炸药与覆冰、 输电线之间的相互作用. 炸药与空气采用Euler算法， 覆冰和输电线采用Lagrange算法， 网格尺寸为1 mm， 采用Lagrange网格进行建模和计算， 覆冰与导线间采用固连断开模型， 炸药与覆冰之间的相互作用采用接触算法控制， 来模拟覆冰的侵蚀.

2.1 有限元计算模型

文中电线直径25 mm， 覆冰厚度25 mm， 导爆索ρL=6.0 g/m， 长度为0.6 m. 考虑到网格划

分质量问题， 将圆形导爆索横截面简化为正方形， 根据以往模拟经验， 该简化算法对爆炸作用效果的影响可以忽略， 其有限元计算模型如图 1 所示.

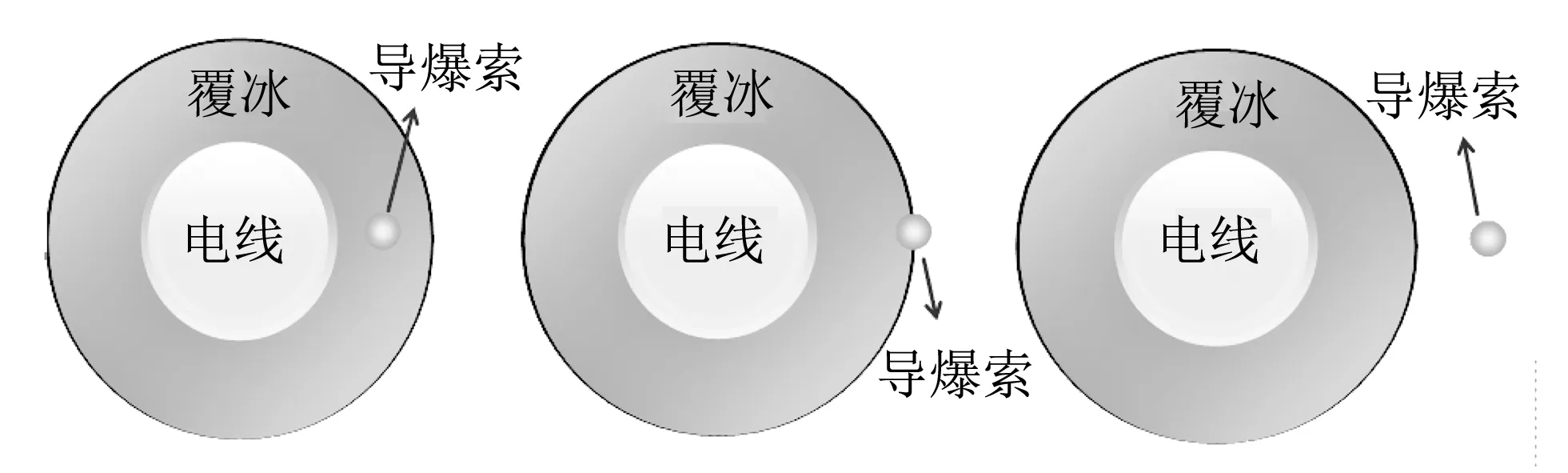
图 1 有限元模型Fig.1 Finite element model

2.2 冰的参数

冰的参数主要包括密度以及冰与输电线路表面的摩擦系数. 根据不同地段的覆冰情况， 分析其覆冰的密度， 仿真中采用相对应的覆冰密度， 如表 1 所示； 冰与输电线路表面的摩擦系数通过摩擦系数测试实验得到.

表 1 冰的相关参数[15-16]

2.3 炸药的模型参数

数值模拟中炸药材料模型采用LS-DYNA材料库中的MAT_HIGH_EXPLOSIVE_BURN模型， 该模型的结构主要由爆速、 密度状态以及爆炸压力三个方面组成. 炸药起爆之后的爆轰产物体积变化规律采用典型的JWL状态方程， 其模型中的压力可由内能及相对体积的相关函数来描述， 表达形式为

(3)

式中：e为比内能， 表示单位质量炸药所含的内能，R1,R2,A、B以及ω均为由模型(3)拟合实验结果获得的常数.η=ρ/ρ0为起爆之后的爆轰产物与炸药没有起爆之前密度之间的比值. 该数值模拟研究中采用的炸药为RDX基复合材料炸药， 因此， 其状态方程中的参数有两种选择情况： ① 直接应用起爆之后的爆轰参数； ② 可根据爆热关系将RDX基复合炸药换算为TNT炸药， 数值模拟直接应用TNT炸药参数. 本数值模拟研究中的炸药直接采用含有20%铝粉复合炸药的JWL状态方程参数， 其具体参数如表 2 所示.

表 2 RDX炸药和TNT炸药JWL参数[15-16]

2.4 空气模型参数

由*MAT_NULL控制空气介质材料模型， 并应用*LNIEAR_POLYNOMIAL MODEL描述空气介质状态， 其表达形式为

p=c0+c1μ+c2μ2+c3μ3+(c4μ+c5μ2+c6μ3)E,(4)

式中：μ为比容；c0,c1,c2,c3,c4,c5,c6表示实验研究常数， 在空气当中，c0=c1=c2=c3=c6=0，c4=c5=γ-1，γ为比热比；E为单位体积能量. 空气状态方程相关具体参数如表 3 所示， 其表达形式为

(5)

表 3 空气的状态方程材料参数[15-16]

2.5 输电线模型参数

数值模拟中的输电线采用主体材料为铝合金绞线， 可应用应变强化弹塑性模式描述其响应特性， 该模型能够较好地描述材料随动硬化行为， 以及各向同性力学行为， 可应用于多种不同单元类型， 材料应变率效应可采用Cowper-Symonds进行描述[15-16]， 其表达式为

(6)

式中：σ0为材料静态屈服应力;σd为材料动态屈服应力;C和P均为应变率效应相关项参数. 在纯铝材料中， 其应变率效应表现更为明显， 但目前研究的绝大部分铝合金材料其应变率效应不明显， 因此， 在本数值模拟研究中， 不考虑输电线的应变率效应， 其具体参数如表 4 所示.

表 4 模型参数[15-16]

2.6 模拟结果与讨论

控爆参数的计算主要包含两方面： 输电线覆冰除冰的效果， 炸药起爆后的冲击波对输电线及塔的动态力学响应. 通过炸药在输电线上的不同间隔分布， 以除冰效果为评估依据， 获得输电线上炸药的最佳分布方式.

为研究装药间隔δ对输电线路除冰效果影响， 进行5组装药间隔数值模拟研究， 装药间隔分别为15, 20, 25, 30以及40 mm. 由数值模拟研究结果以及表 5 可知， 装药间隔在15, 20, 25, 30 mm 时， 输电线路上的覆冰全部脱落， 图2为装药间隔30 mm时的除冰情况， 由图可知， 除冰效果显著， 达到预期除冰目标要求.

表 5 不同炸药间隔脱冰情况

图 2 装药间隔为30 mm的模拟结果Fig.2 Simulation results of 30mm charging interval

结合实际除冰情况， 对于装药间隔δ而言， 设计δ过小， 则爆炸容易损伤导线， 产生毛刺、 塑性变形甚至裂纹， 增大断线的危险性. 但如果δ过大， 一方面覆冰厚度小于δ时， 对应于之前实验中采用的导爆索位于覆冰之外的工况， 空气衰减层的存在不利于爆破除冰； 另一方面，δ过大在实际施工过程中不便于导爆索和导线的平行布设， 也不利于导爆索防绕线扭转等情况的控制， 因此根据实际覆冰除冰需求和考虑实际施工控制， 炸药间隔在30 mm时除冰效果较为理想. 为进一步验证数值模拟仿真计算结果， 进行缩比爆破除冰实验研究.

3 缩比爆破除冰实验验证

根据输电线路的实际工况， 以爆破除冰数值模拟为指导， 对输电线路爆破除冰进行缩比实验， 其中模拟导线直径为25 mm， 覆冰厚度为25 mm， 导爆索ρL=6.0 g/m， 两端角钢固定约束， 导爆管雷管引爆.

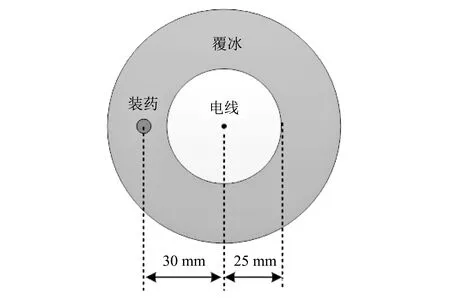
图 3 缩比实验装药分布形式Fig.3 Distribution pattern of scaled experiment charging

导爆索与模拟导线间距为30 mm(模拟导线中心位置至导爆索间距)， 如图 3 所示， 缩比爆破实验中高速相机拍摄帧率为40 000 fps. 图 4 为高速相机拍摄到的缩比爆破除冰实验及仿真除冰情况， 由图可知， 缩比爆破除冰效果较为理想， 从起爆开始， 到模拟导线上覆冰全部去除， 所需时间约为40～50 μs， 爆破除冰效果显著， 与数值模拟仿真结果基本吻合.

图 4 实验与仿真除冰情况Fig.4 Experiment and simulation of deicing condition

4 结 论

1) 有效覆冰参数， 以及高压输电线与覆冰表面摩擦系数的确定为爆破除冰控爆参数计算提供了重要参数.

2) 以除冰效果及输电线的动态力学响应为依据， 通过控爆参数有效模拟仿真计算， 确定了输电线(直径为25 mm)上25 mm厚的覆冰最佳除冰方案： 线装炸药ρL=6.0 g/m， 装药与导线中心位置间隔值为30 mm.

3) 缩比爆破除冰实验验证了爆破除冰控爆参数的可靠性及可行性， 研究结果可为高压输电线路爆破除冰设计提供依据.