混合自适应动态规划和蚁群算法的agent路径规划
周丽娟
(山西财经大学 实验教学中心, 山西 太原 030006)
多agent的路径规划是智能规划领域的一个研究重点[1-2]. agent规划任务是要寻求从初始位置到目标位置的一条可行路径. 多agent的动态路径规划是指多个agent从不同的初始位置同时出发, 在未知的环境中通过学习, 避开所有障碍物, 寻求到不同目标位置的路径.
常用的求解方法包括模糊神经网络方法[3]、 智能优化算法[4-9]、 动态规划方法[10-11]以及启发式搜索方法[12]. 钱夔[3]等提出了一种模糊神经网络方法, 采用神经网络对输入量进行模糊处理, 并建立基于输出量的逻辑规则, 求解的策略是基于输出量和逻辑规则来生成最优规划路径. 伍永健[4]等提出了一种基于量子粒子群和Morphin算法的混合路径规划方法. 首先, 通过栅格离散化方法建立环境模型, 建立自适应的局部搜索策略和交叉操作对粒子群算法改进, 从而规划出最优路径. 王学武[5]等将点焊机器人的路径规划问题转换为焊接顺序的优化问题, 设计一种基于莱维飞行的粒子群算法来求解路径优化问题. 屈鸿[6]等设计了一种改进的蚁群算法[7-9], 通过引入相关策略避免死锁问题, 通过调整转移概率来限定信息素强度上下界, 并提出了相应的碰撞避免策略. 唐振民[10]等充分考虑多机器人系统的动态特征, 运用Dijkstra算法和图论的相关知识, 求解路径规划. 朱广蔚[11]等提出了一种基于动态规划方法的路径规划方法, 首先寻找图中的包含所有节点的TSP回路, 然后利用动态规划来对回路分段, 以最小化路径总距离和关键负载为目标. 陈洋[12]等将完成目标序列访问任务的总时间最短为代价, 建立目标优化模型, 将机器人路径规划问题转换为混合整数凸优化问题.
除了这些常见方法, 还有一些方法是将以上多种方法进行结合[13-17], 这些方法虽然提供了路径规划更灵活的求解方式, 但是仍然主要针对单agent的规划场景, 同时大部分工作没有考虑到障碍物的随机动态变化. 强化学习[18-19]是一种通过最大化长期的累计奖赏来获取最优策略的方法, 能通过在线学习快速学习到agent的最优策略, 能适合多agent共寻优的要求. 因此, 本文研究基于强化学习并立足于解决多agent的并行路径规划问题, 同时场景动态实时变化.
为了解决该问题, 本文提出一种基于动态规划和混合蚁群算法的多agent路径规划方法, 采用蚁群算法来初始化经过栅格化的各个位置点处的信息素, 针对每个agent的初始位置和目标位置, 采用动态规划方法实时规划出一条最优路径, 从而实现多条路径的并行实时规划.
1 agent输入输出设置
agent 附加了多个传感器来感知环境状态, agent 的输入来自传感器所感知的状态, 而输出则是根据自适应动态规划获得的最优策略, 如图 1 所示.

图 1 agent传感器设置图Fig.1 Setting of the sensors of agent
agent被安置了6个传感器, 其中5个为距离传感器, 分别为前置传感器、 左置传感器、 右置传感器、 左前传感器、 右前传感器, 用于对周边环境状态进行检测, 测量出机器人在当前动作执行后移动的距离值, 对应的传感器测量的距离值分别为:d1,d2,d3,d4和d5. 还有一个传感器为目标传感器, 用于检测目标所在方向与机器人行进方向的夹角θ.
所有传感器测量的数据都将被归一化处理, 对于距离传感器, 其数据归一化的方式为(i=1,2,…,5)
(1)
式中:l是测量距离的最大值, 因此, 距离值xi经过归一化后, 将会位于[-1,1]之间, 当xi=-1时, 表示机器人撞到障碍物; 当xi=1时, 表示机器人到达了终点; 当xi=0表示未检测到障碍物或目标. 目标传感器主要读取的两个值θ1和θ2, 分别为移动机器人前进方向和水平方向夹角和目标与机器人前进方向的夹角. 目标传感器的测量值为: Δθ=θ1-θ2, 则目标测量值可以表示为
Δθ=θ1-θ2.(2)
归一化后的目标传感器值可以表示为
(3)
归一化的位置传感器和目标传感器构成的状态X=(x1,x2,x3,x4,x5,θ). 在某时刻, 当机器人以常速在环境中行驶, 根据输出策略u的值, agent调整其前进方向, 当策略值u>0时, agent向左调整其前进方向20°, 当u<0时, agent向右调整其前进方向-20°, 当u=0时, agent保持前进方向.
2 基于蚁群的值函数初始化
2.1 蚁群算法
蚁群算法是由Dorigo于20世纪90年代提出的仿生智能算法. 当经过某条路径的蚂蚁数量越多, 就会留下越多的信息素, 使得后面的蚂蚁选择信息素较多的路径的可能性更大, 而这些信息素较多的路径很可能就对应了短路程的路径.
在初始时刻, 蚂蚁位于相同的初始位置处, 场景中的每个可能的位置点处都分布一定的初始信息素, 假设某条较短的路径为S, 较长的路径为L, 经过S和L的蚂蚁数量分别为M1和M2, 经过这两条路径的蚂蚁总和为
M=M1+M2.(4)
当M只蚂蚁行走过后, 则第M+1只蚂蚁选择路径S的几率为
(5)
式中: 参数a和b为位于[0,1]之间的数. 设计一个阈值b, 如果PM(S)>h时, 将会选择路径S, 否则会选择路径L.
2.2 信息素更新
蚂蚁在路径上留下的信息素会使得这些区域对蚂蚁来说具有吸引力, 而信息素会随着时间挥发, 采用GBA/stlb信息素更新策略
(6)
式中:ρ为信息素挥发因子;Γ*(n)表示上一个周期的最优路径. 从式(6)可以看出, 未被选择路径在下一个搜索周期中, 信息素会随着时间挥发而逐渐变少.
2.3 基于蚁群算法的值函数初始化
采用蚁群算法更新值函数的方法为:
输入: 参数a和b, 蚂蚁的数量NC, 信息素挥发因子ρ, 任意位置到下一位置的信息素τi,j;
初始化: 环境模型, 对环境场景中所有位置点的信息素进行初始化, 当前蚂蚁数量N=1;
1) 设定蚂蚁的初始位置和目标位置, 将蚁群的位置置于初始位置点;
2) 蚂蚁根据各路径上的信息素, 根据转移概率来移动到下一个位置点;
3) 根据式(6)来更新信息素;
4) 当蚂蚁没有达到目标位置时候, 则重新下一位置的移动概率, 并根据移动概率来移动到一个位置, 同时更新信息素; 否则, 就从蚁群中派出下一只蚂蚁, 并使得蚂蚁从步骤1)开始继续执行;
5) 当所有蚂蚁都找出最优路径时, 根据各位置点上的信息素来初始化和更新值函数;
6) 算法结束.
输出: 将求出的信息素τi,j转换为初始的值函数.
采用蚁群算法来初始化值函数的流程, 如图 2 所示.

图 2 基于蚁群算法的值函数初始化Fig.2 Initialization of the value function based on ant colony algorithm
3 基于自适应动态规划的agent路径规划
3.1 自适应动态规划
动态规划方法是一种基于模型的强化学习方法, 通过不断迭代贝尔曼方程来求解最优值函数. 然而, 在通常的强化学习场景中, 模型是未知的, 因此, 无法直接通过动态规划的两类方法, 值迭代算法和策略迭代算法, 来求解最优值函数.
Q学习作为一种基于样本的值迭代算法来求解, 能在无需动态性模型的情况下, 仅需在线获取样本就能实现值函数的学习. 在采用Q学习值函数学习时, 需要设定奖赏函数和迁移函数.
奖赏函数的设置为学习到目标状态后, 获得一个值为0的立即奖赏, 而在其它位置获得值为-1的立即奖赏. 迁移函数的设置是根据agent距离传感器测量出的距离来确定x方向的坐标值和y方向的坐标值.
3.2 基于自适应动态规划的agent规划算法
采用自适应动态规划来实现agent路径规划的算法如算法1所示, 即采用改进的Q学习来求解agent最优路径的规划算法.
算法 2 基于Q学习的agent最优路径规划算法
输入: 动作探索因子ε, 折扣率γ, 学习率α, 最大情节数Emax, 情节的最大时间步Smax;
初始化: 设置任意状态动作处(x,u)的Q值为0, 即Q0(x,u)=0, 设置当前状态为初始状态x=x0, 当前情节数E=1, 当前时间步S=1;
1) 根据状态x处Q值来确定最优动作
2) 采用ε贪心策略来选择当前状态处的动作
3) 根据迁移函数来获得当前状态和动作执行后获得的后续状态x′和立即奖赏r;
4) 根据状态x′处Q值来确定最优动作
5) 采用ε贪心策略来选择下一状态x′处的动作
6) 更新当前状态动作对(x,u)的Q值
Q(x,u)=
Q(x,u)+α(r+γ(Q(x′,u′*)-Q(x,u)).
7) 更新当前状态:x←x′
8) 更新下一个状态处执行的动作
u←u′;
9) 更新当前时间步S=S+1, 如果S不超过Smax, 则转入1)继续执行;
10) 更新当前情节数E=E+1, 如果E不超过Emax, 则转入1)继续执行;
输出: 任意状态动作对应的Q值, 从而获得沿着每个状态处的最优动作, 即最优路径.
算法2所示的基于Q学习的agent最优路径规划算法如图 3 所示.

图 3 基于Q学习的路径规划算法Fig.3 Route planning algorithm based on Q-Learning
4 仿真实验
4.1 实验描述
在Matlab仿真环境下, 对文中所提方法进行验证. 仿真场景图如图 4 所示, 其中黑色阴影部分为障碍物, agent移动的初始位置在左下角处, 而右上角则是移动的目标位置.
4.2 场景栅格化
为了对仿真场景进行量化, 对二维环境场景进行栅格化, 对x轴方向和y轴方向分别进行等分成20份来进行栅格化, 栅格化的结果如图 5 所示.

图 4 迷宫仿真场景图Fig.4 Setting of the maze

图 5 环境场景栅格化图Fig.5 Discretization of the maze
4.3 最优路径的获取
为了获得agent从初始位置到目标位置的最优路径, 首先采用蚁群算法来对场景中各个状态处的值函数进行初始化, 然后再通过自适应的动态规划算法来求取各个状态动作处的最优动作之后的函数, 从而获得各状态处最优动作.
参数设置为: 参数a=0.4和b=0.6, 蚂蚁的数量NC=200, 信息素挥发因子ρ=0.4, 任意位置到下一位置的信息素τi,j=0.5. 动作探索因子ε=0.05, 折扣率γ=0.9, 学习率α=0.5, 最大情节数Emax=300, 情节的最大时间步Smax=200.
下面在障碍物分布固定和障碍物分布随机两种情况下对迷宫场景进行分析, 障碍物固定是指障碍物的位置是在实验初始化时就固定, 而障碍物分布随机是指障碍物在初始时刻的位置是随机分布的(通过随机函数在当前迷宫状态空间中随机生成的位置), 较固定情况时更能对算法的鲁棒性进行测试.
1) 在障碍物固定的情况下, 当算法运行完后, 得到的agent从初始位置到目标位置的最优路径为图 6 所示.
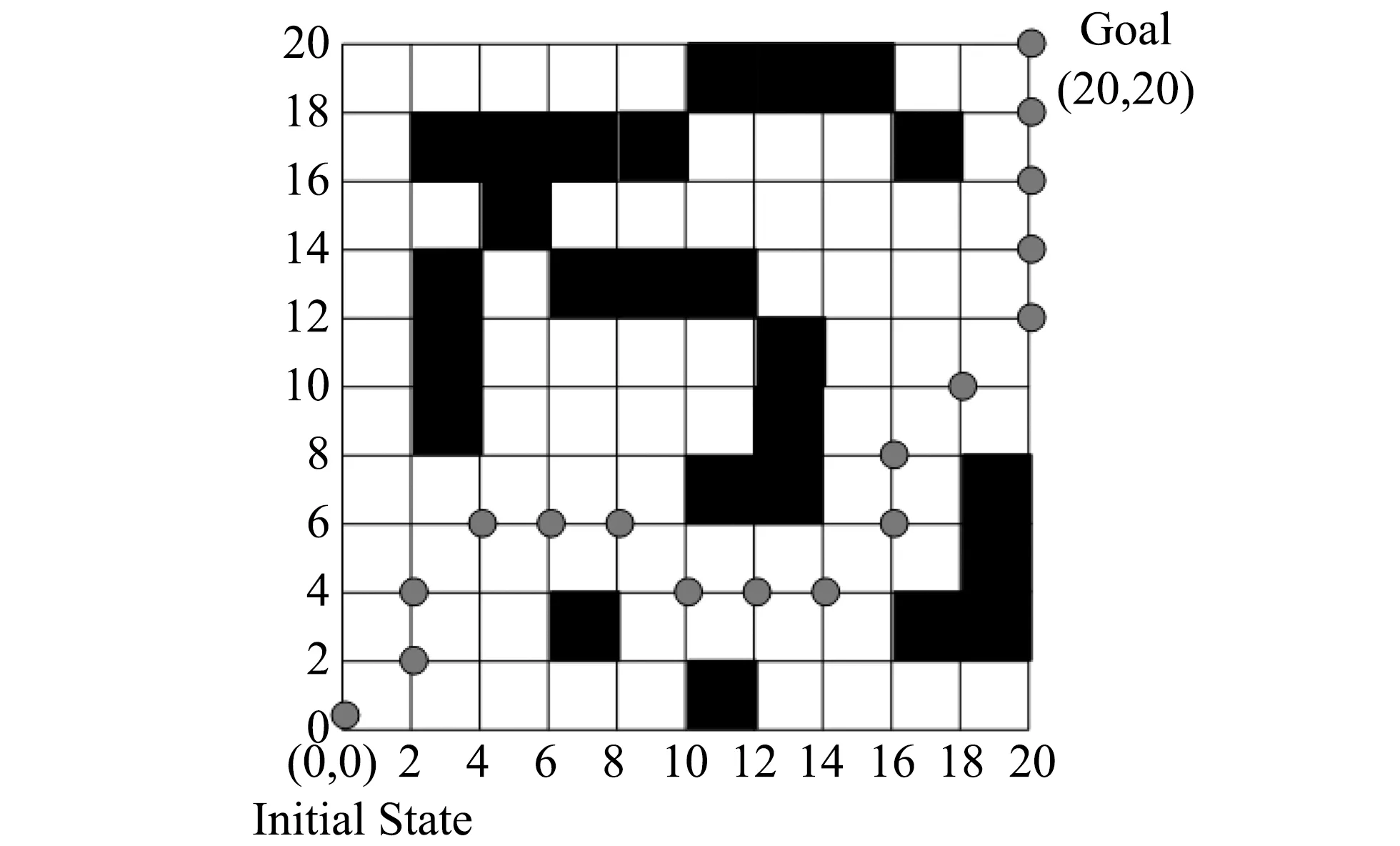
图 6 固定障碍物下的最优路径Fig.6 Optimal route with the fix barrier
2) 当初始时刻的障碍物随机分布时, 此时的场景如图 7 所示.

图 7 随机障碍物下的仿真场景Fig.7 Maze scenario with the random barrier
算法运行完后, 得到的agent从初始位置到目标位置的最优路径为图 8 所示.

图 8 随机障碍物下的最优路径Fig.8 Optimal route with the random barrier
4.4 比较与分析
为了进一步验证文中方法的优越性, 将文献[9]中基于蚁群算法的规划方法以及文献[10]中基于动态规划的方法进行比较, 在固定障碍物的情况下, 三种方法得到的收敛所需的时间步随情节增加的变化如图 9 所示.

图 9 固定障碍物下的方法比较Fig.9 Comparisons of different methods with the fix barrier
从图 9 可以看出, 本文方法的收敛速度最快, 大约在210个情节后收敛, 而文献[9]和文献[10]方法在240个情节和300个情节后开始收敛, 但收敛后所需要的时间步为18, 大于本文方法所需的17个时间步.
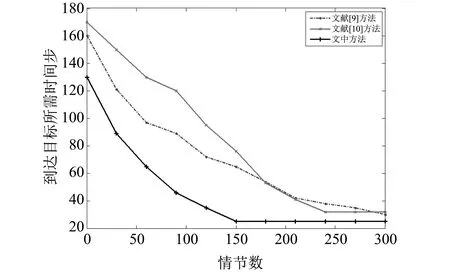
图 10 随机障碍物下的方法比较Fig.10 Comparisons of different methods with the random barrier
从图 10 可以看出, 在随机障碍物下, 本文方法的收敛速度最快, 大约在150个情节后收敛, 收敛所需的时间步为25, 而文献[9]始终未能收敛, 而文献[10]方法虽然收敛, 但收敛时所需的时间步为32. 显然, 本文方法远远优于文献[9]方法和文献[10]方法.
三种方法在固定障碍物和随机障碍物情况下对应的收敛性能如表 1 所示.
从表 1 可以看出, 本文方法相对于文献[9]和文献[10]方法, 不仅具有较快的收敛速度, 而且具有更好的收敛精度.

表 1 收敛性能比较
5 结 论
为了实现agent的最优路径规划, 提出了一种混合自适应动态规划和蚁群算法的agent路径规划方法. 首先, 根据agent配置的传感器对系统状态的输入和输出进行了定义. 然后, 采用改进的蚁群算法来更新路径中各个位置的信息素, 并根据更新的信息素来初始化值函数. 此后, 采用改进的自适应动态规划算法来进一步更新值函数, 直至值函数收敛. 根据最优值函数实现任意状态到动作的映射, 从而求解出agent从初始状态到目标状态的最优路径. 在文中对两个算法均进行了仔细的定义和描述. 通过仿真实验证明了文中方法无论是在固定障碍物还是在随机障碍物情况下, 都具有收敛速度快和收敛精度高的优点.

