热脉冲-时域反射技术原位测定土壤孔隙度及其影响因素分析

刘晓娜， 丁庆伟

(太原科技大学 环境与安全学院， 山西 太原 030024)

0 引 言

土壤孔隙度(n)影响着土壤的通气透水性能[1]、 土壤中微生物的活性以及CO2和N2O等气体在土壤中的产生与传输等一系列过程[2]， 是研究农田生态系统的重要物理参数.

土壤孔隙度一般根据土壤容重计算而得. 而利用传统测量土壤容重的方法测定土壤孔隙度， 或多或少存在一定的局限性. 测定土壤容重的传统方法主要有环刀法、 蜡封法和γ射线法等[3]. 环刀法与蜡封法操作简便， 结果准确. 但由于土壤容重的空间变异性， 需要较大数目的样品方可得到具有代表性的观测值. 同时， 田间采样费时费力， 对土壤破坏严重， 在同一地点不可重复取样测定， 难以实现定位观测[4].γ射线法对土壤结构影响轻微、 测定迅速、 可以进行定点测定， 但测定土壤容重时的标定需求以及不可避免的辐射危害限制了该技术在科研和生产中的广泛应用. 近年来， 随着介电技术(特别是TDR技术)在介质物理特性测定中的应用， 测定多孔介质容重的技术得到了一定发展. Trabelsi等通过测定特定频率微波下容器内谷物种子的介电常数， 得到了种子的容重[5]. 该方法对介质结构无任何破坏作用， 可以用于动态监测容重， 但需要首先建立标定方程， 而且局限于实验室应用. Yu 和 Drneivich 发展了常规时域反射(TDR)方法， 提出了Purdue TDR技术， 在获得田间土壤含水量和容重的信息的同时实现了温度变化对测定结果影响的校正[6]， 但不足是经验方程中的参数值只能通过室内标定获得， 而且不同质地土壤的参数差异较大， 需要分别标定， 实际应用中很不方便. Fratta等采用TDR系统和压电式加速度表测定了一定水分梯度下的土壤含水量和P-波速率， 并进一步利用模型反求出了土壤容重[7]. 该技术测定容重的精确度较高， 但需要人为创造田间土壤水分梯度， 测定和计算过程中比较繁琐， 而且难以实现连续观测. 此外， 土壤容重和孔隙度随时间呈现动态变化特征[8-10]， 理想的测定技术应当在农田条件下完成孔隙度的连续定位监测. 而由于传统方法测量的局限性， 目前还没有关于土壤孔隙度动态监测方面的研究.

Ren等[11]建立了Thermo-TDR技术， 提出了利用Thermo-TDR技术测定土壤容重和孔隙度的理论[12-13]. 热脉冲-时域反射技术的出现， 满足了动态监测土壤容重的要求. 而针对热脉冲-时域反射技术测量田间土壤容重时准确性较低的问题， Liu等[14]根据前人对影响热脉冲技术测量精度的关键因素的分析[15-18]， 结合热脉冲探头和时域反射探头的设计标准， 在Ren等[11]常规探头基础上， 对Thermo-TDR探头进行了优化， 实现了土壤容重的准确原位动态监测[19]. 本文利用热脉冲-时域反射探头原位动态监测不同含水量和容重下的充气孔隙度， 并对热脉冲-时域反射技术测定土壤充气孔隙度的影响因素进行分析.

1 材料与方法

1.1 测定原理

土壤孔隙度(n)和充气孔隙度(na)通常由土壤容重计算得到[20]

(1)

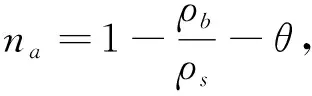
式中：ρs为土粒密度， kg·m-3；θ为土壤的容积含水量， m3·m-3；ρb为是土壤的容重， kg·m-3， 由热脉冲-时域反射技术得到.

1.2 Thermo-TDR探头

热脉冲-时域反射探头结构如图 1 所示. 图 1(a)为Ren等[11]常规探头， 图 1(b) 为Liu等[14]改进后的探头. 二者构造基本相同， 均由三根不锈钢管组成， 不锈钢管内部填充加热丝和热电偶. 但探针长度和间距略有不同. Ren等[11]常规探头钢管直径1.3 mm， 长40 mm， 间距为6 mm. Liu等[14]改进后的探头钢管直径2 mm， 长45 mm， 间距为8 mm， 且探针末端为尖头. 本研究中室内和野外实验均采用图 1(b) 的探头. 实验过程中， Thermo-TDR探头与数据采集仪和电缆测试仪相连， 电缆测试仪自动采集TDR波形， 利用Topp等[21]公式计算得到土壤含水量； 数据采集仪记录热脉冲数据， 根据热传导方程得到土壤的容积热容. 而利用土壤热容量与含水量的关系， 即可计算的到土壤的容重， 从而进一步得到土壤孔隙度和充气孔隙度.

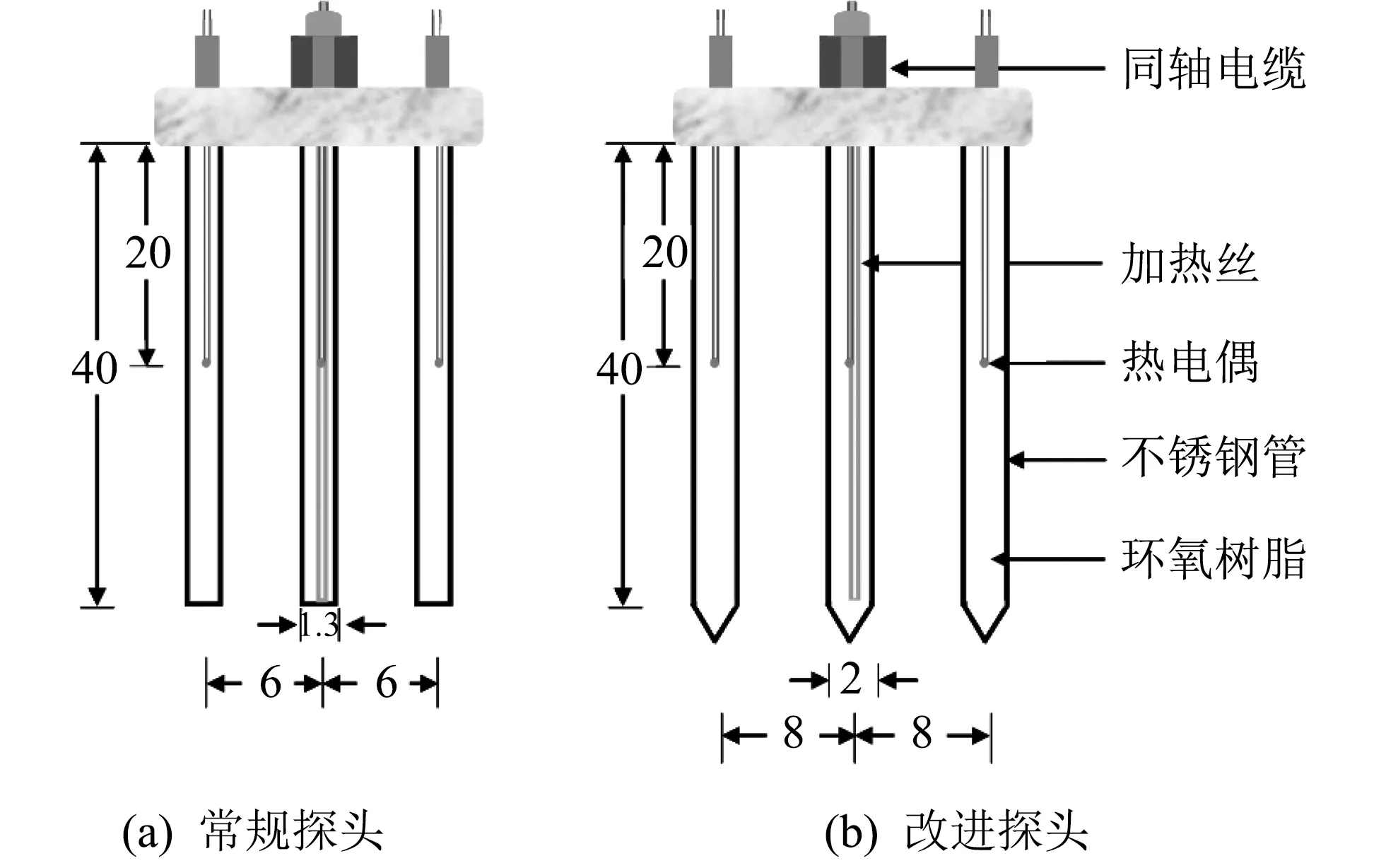
图 1 Thermo-TDR探头结构示意图Fig.1 Schematic view of Thermo-TDR sensor

1.3 实验测定

室内实验采用三种不同质地的土壤(粉壤， 砂土及粘壤)， 首先将土壤样品风干， 过筛(2 mm)， 然后按不同含水量和容重填装土柱. 最后将土柱用保鲜膜密封， 以防止水分的蒸发损失， 置于恒温室中(20±1 ℃)24 h后进行测定. 野外实验选择质地为壤土的耕地休闲地. 首先， 将0～30 cm土层进行翻耕使得土壤自然均匀疏松. 然后， 人工挖一土壤剖面(深20 cm)， 将Thermo-TDR探头插入距地表5 cm 和15 cm处即测定0～10 cm和10～20 cm土层数值. 24 h后， 待探头与土壤周围环境温度平衡后， 开始进行测定. Thermo-TDR技术详细测定方法可参阅Liu 等[16]. 测定完成后， 在探头周围环刀取样， 利用烘干法测土壤容重和孔隙度， 与Thermo-TDR值进行比较. 田间试验持续41 d， 整个实验持续过程中， 未采取任何人为耕作措施， 土壤容重和孔隙度的变化受降雨后土壤的干湿交替等自然过程影响. 测定时间间隔取决于田间土壤容重和孔隙的实际变化情况. 实验设五个重复， 所有数据取五个重复的平均值.

2 结果与讨论

2.1 室内不同质地土壤的孔隙度测定

图 2 是实验室内对三种不同质地土壤孔隙度及充气孔隙度的测定结果与烘干法测定结果的比较， 图中实线为1∶1线. 从图中可以看出， 所有数据均不同程度自由分布在1∶1线的两侧， 即Thermo-TDR测定值与烘干值较吻合. 对结果进行误差分析， Thermo-TDR孔隙度的均方根误差(RMSE)为0.019， 对土壤充气孔隙度的均方根误差则为0.015. 说明Thermo-TDR探头能准确反映土壤孔隙度的信息.

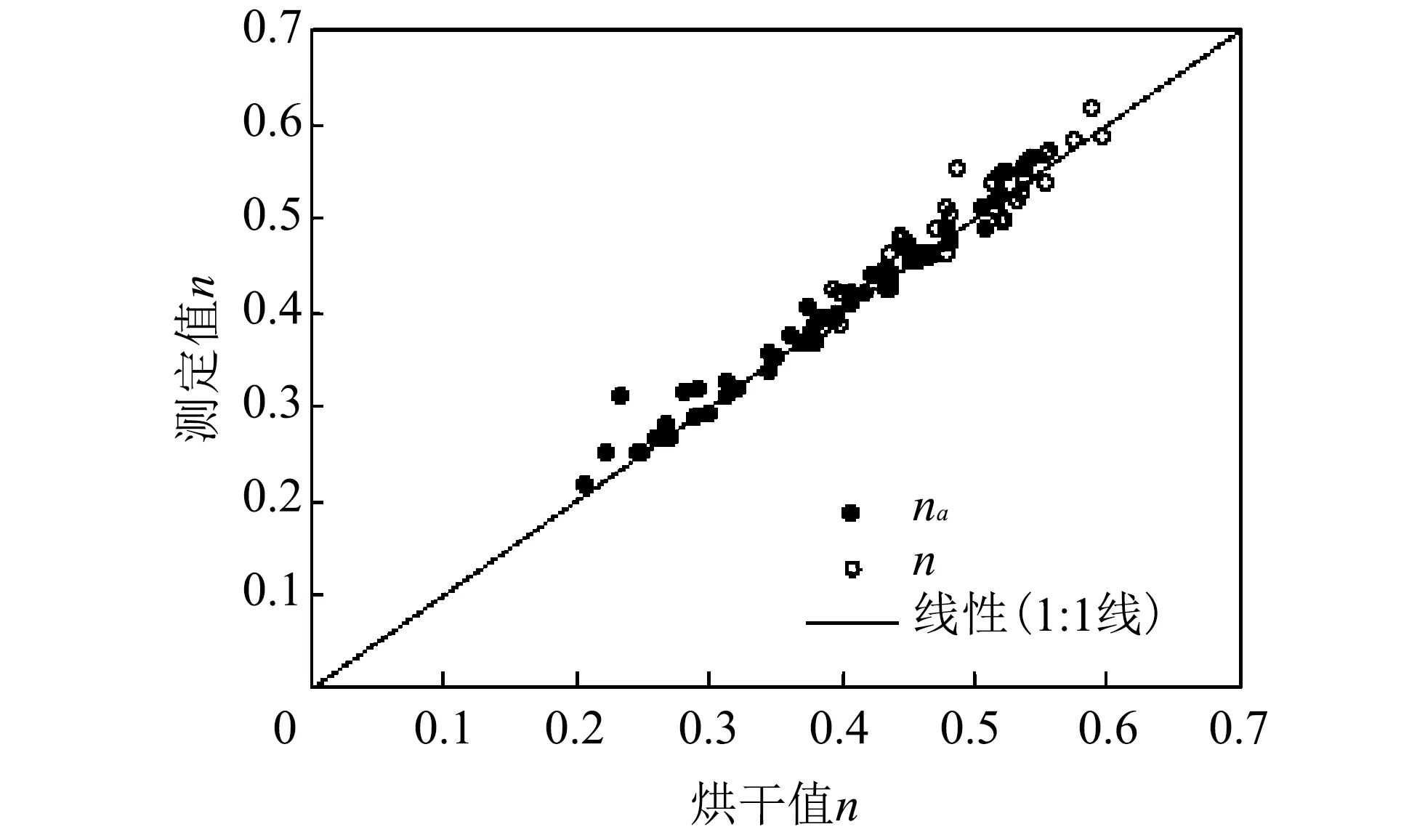
图 2 Thermo-TDR室内土壤孔隙度和充气孔隙度与烘干值的比较Fig.2 Comparison of Thermo-TDR estimated n and na with gravimetric measurement

2.2 野外定位监测土壤孔隙度的动态变化

图 3 展示了田间Thermo-TDR孔隙度动态变化. 图中每一个点是五个点的平均值.

图 3 土壤孔隙度的动态变化图Fig.3 Thermo-time domain reflectometry (TDR) estimated the dynamic n

如图 3 所示， Thermo-TDR孔隙度能准确反映出田间土壤孔隙度的动态变化过程. 整个实验过程中， 土壤孔隙度的变化大致可分为两个阶段， 第一个阶段从第10 d到第41 d， 土壤孔隙度以一定的速率快速地由初始值0.62左右下降至0.51， 在第二个阶段， 即第41 d以后， 土壤孔隙度变化缓慢， 到最后基本不再发生变化. 从实验测定开始计算， 大约30 d左右， 土壤孔隙度能基本达到稳定状态， 变化不再明显. 另外， 从图中可以看出， 不同土层即0～10 cm和10～20 cm两个土层的孔隙度的变化情况基本相同， 不存在明显差异. 主要原因有： 首先， 在开始测定前， 表层土壤经过翻犁， 初始土壤容重上下一致， 孔隙度相同， 不同土层间不存在差异； 其次， 土壤孔隙状况是一个随时间变化的动态性质， 主要是受土壤水分及温度的影响， 在本实验中， 土壤容重和孔隙度的变化主要依赖于土壤自身的干湿交替过程， 无人为干扰因素； 最后， 实验时间持续51 d， 时间较短. 因此， 不同土层间土壤孔隙度差异不明显.

2.3 Thermo-TDR土壤充气孔隙度与烘干值的比较

Thermo-TDR测定土壤充气孔隙度结果与烘干实测值的比较见图 4. 由图 4 可见， 所有数据点较好地分布在1∶1线的两侧. 均方根误差RMSE值为0.023； 与烘干实测值进行比较， 所有Thermo-TDR数据结果的相对误差都在5%以内， 能准确地反映土壤充气孔隙度的信息.

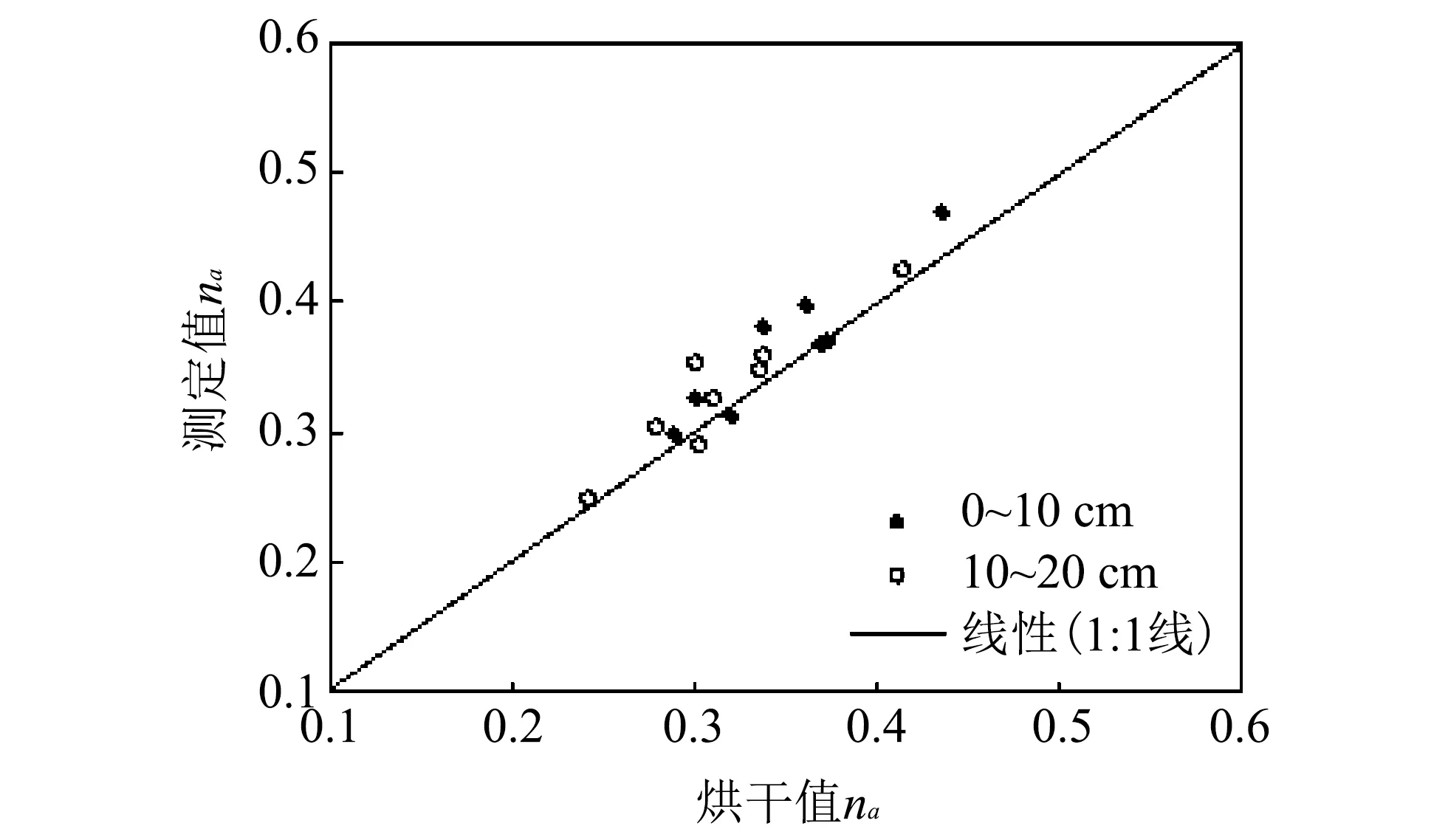
图 4 Thermo-TDR充气孔隙度与烘干值的比较Fig.4 Thermo-TDR estimated na versus gravimetrically measured na

实验过程中， Thermo-TDR探头定位监测土壤孔隙度的动态变化， 每次测定完成后， 用环刀在尽量靠近探头的位置取样计算烘干值， 而取样位置与测定位置的空间差异使Thermo-TDR孔隙度与烘干值之间存在误差. 为检验此误差对实验结果的影响程度， 在最后一次测定完成后， 在探头插入位置环刀取样， 计算得到孔隙度烘干数值， 并与Thermo-TDR土壤孔隙度进行了比较. 经测定， Thermo-TDR技术得到不同土层(0～10 cm和10～20 cm)的孔隙度数值分别为0.498和0.501， 而对应烘干的实测孔隙度数值为0.505和0.506， 可见， Thermo-TDR测定的孔隙度值是准确可靠的.

2.4 热脉冲-时域反射技术测定土壤充气孔隙度的影响因素及误差分析

在热脉冲理论中， 假设无限长的线性热源置于无限大的且均匀的等温介质中瞬时加热， 土壤的容积热容量与最大温度升高值之间的关系方程无法进行偏微分运算， 为便于进一步计算分析， 本文采用此公式的简化表达式[22]

(3)

式中：C为容积热容量， J·m-3·℃-1；q为单位长度的热源的热量输入， J·m-1;Tm是距离线性热源r处的最大温升， ℃.

土壤的容积热容量可以近似表达为[3]

C=Cwθ+ρbcs,(4)

式中：Cw是水的容积热容量， J·m-3·℃-1；θ是土壤的容积含水量， m3·m-3；ρb是土壤容重， Mg·m-3；cs是土壤固体的比热， kJ·kg-1·℃-1. 把式(4)代入式(3)中， 则有

(5)

进一步， 充气孔隙度则有

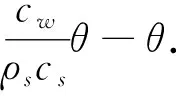
可以看出， 热脉冲技术测定土壤孔隙度的误差与含水量θ、 固体比热cs、 热量q、 间距r和最大温升Tm有关. 式(6)的一阶误差分析[23]表达式为

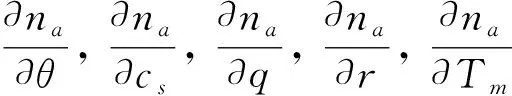
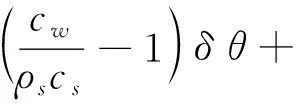
通过公式(8)， 可以计算出热脉冲测量中各个变量即含水量θ、 固体比热cs、 热量q、 间距r和最大温升Tm等的测量误差对土壤充气孔隙度的测量结果准确性的影响[24].

首先， 设定有关变量的初始值，θ取0.2 m3·m-3,cs为0.8 kJ·kg-1·℃-1,q为0.9 kJ·m-1， 以及r为6 mm. 为了考虑各因素对充气孔隙度的影响程度， 选择了三个不同的容重值， 即ρb=1.0， 1.3 和1.6 Mg·m-3. 则通过式(5)计算得到对应的一系列Tm值， 分别为1.79， 1.56和1.38 ℃， 通过式(6)计算得到相应的na值， 分别为0.423， 0.309和0.196.

其次， 将给定的各个变量θ,cs,q,r和Tm等的数值代入式(7)， 可以计算得到各个变量的敏感系数.

最后， 将得到的敏感系数乘以δθ,δcs,δq,δr的值就得到δna值， 其值大小可以说明θ,cs,q,r等变量对土壤充气孔隙度的影响程度. 这里，δθ,δcs,δq,δr分别取设定的θ,cs,q,r值的5%. 例如，θ的给定值为0.2 m3·m-3， 则θ的5%的偏差将造成δθ=0.01 m3·m-3， 再乘以敏感系数-0.91 m3·m-3则计算得到δna=-0.009 Mg ·m-3， 说明含水量的0.01 m3·m-3的正偏差将造成孔隙度0.009 Mg·m-3的负偏差.Tm值对土壤孔隙度的影响的计算稍不同于几个变量. 由于不同的土壤孔隙度值计算得出不同的Tm值， 对于δTm取0.05 ℃， 将敏感系数乘以0.05 ℃， 则分别得到δna=0.022 Mg·m-3(na=0.4)，δna=0.029 Mg·m-3(na=0.3)和δna=0.036 Mg·m-3(na=0.2).

敏感系数及各变量影响的δna值计算结果均列在表 1 中， 可以看出，θ的敏感系数不随土壤容重值的变化而发生变化. 而随着孔隙度值的降低，cs,q,r和Tm等的敏感系数则相应增大. 另外， 通过各个δna值的大小， 可以看出θ,cs,q,r和Tm等变量对土壤孔隙度测定结果的影响程度， 其中，q和r值对容重的影响最大， 当土壤容重ρb=1.0 Mg·m-3即na=0.4时， 5%的q和r的误差将带来0.039的土壤充气孔隙度正偏差.

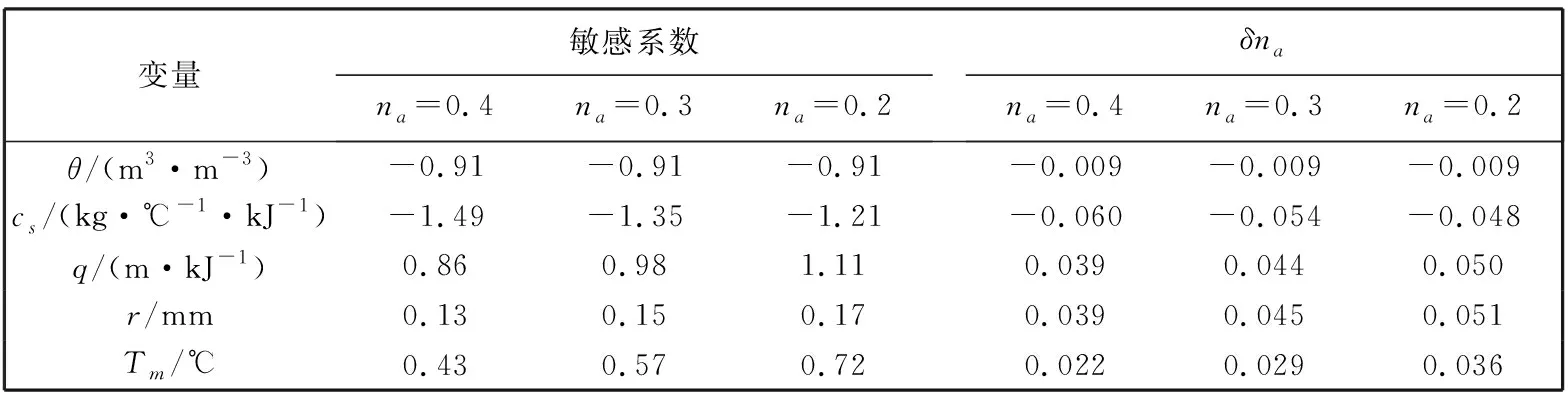
表 1 影响充气孔隙度测定的变量及其敏感系数

综上所述， 热脉冲-时域反射技术测定土壤孔隙度的准确性受土壤含水量(θ)、 土壤固体比热(cs)、 加热过程中能量大小(q)、 探针间距(r)和探针最大温升(Tm)等因素的共同影响， 而r和q的不确定性是误差的最主要来源.

在热脉冲-时域反射技术测定过程中， 电流值是通过测定一个精确电阻(1 Ω)的电压下降(ΔV)来确定的. 加热能量的大小根据土壤含水量调节， 一般保持两侧探针温度的最大升高值为0.8～1.0 ℃. 探头的加热能量

(9)

式中：Rr为探头的总电阻， Ω；Rh为单位长度加热丝的电阻， Ω·m-1；t0为热脉冲持续时间， s.

实验过程中， 可以认定对于热量的输入q的测定是比较准确的， 也就是说q值的测定误差可以被忽略. 因此， 热脉冲-时域反射技术测定土壤容重的误差主要来源于探针的间距r. 在测定过程中， 减少探针入土时的摆动导致的探针间距r变化可以有效降低热脉冲-时域反射技术测定误差.

3 结 论

1) 利用热脉冲-时域反射技术原位动态监测土壤孔隙度， 解决了传统方法不能连续反复测定原状土壤孔隙度的难题.

2) 热脉冲-时域反射技术可以快速准确地反映土壤孔隙度的动态变化和土壤充气孔隙度的信息， 室内测定均方根误差(RMSE)值为0.015， 野外测定RMSE值为0.023， 相对误差在5%以内.

3) 热脉冲-时域反射技术测定土壤充气孔隙度的准确性受土壤含水量(θ)、 土壤固体比热(cs)、 加热过程中能量大小(q)、 探针间距(r)和探针最大温升(Tm)等因素的共同影响， 而r和q的不确定性是误差的最主要来源. 减少探针入土时的摆动导致的探针间距r变化可以有效降低热脉冲-时域反射技术测定误差.