基于三坐标测量机的立方镜标定精度分析
倪爱晶 郭 庆 赵 婕 于望竹 蔡子慧 杨 纯
(北京卫星制造厂有限公司,北京 100094)
1 引 言
航天器总装是将航天器上各分系统装配在一起,形成一个能够完成特定任务的完整系统[1]。航天器装配精度对其功能的实现有着直接影响,装配过程需严格保证重要部件的安装位置与方向,因此总装过程需依赖测量手段保证装配精度,测量对象涉及多种有效载荷,如天线系统、设备、相机等。由于各分系统尺寸大、结构复杂,测量过程中难免出现遮挡导致的不可测量情况。因此,航天器总装中通常引入立方镜作为工艺基准,通过提前标定立方镜和有效载荷的姿态关系,来确定有效载荷的安装位置和姿态。
航天器总装用立方镜是经过精密加工的规则的正方体,根据边长的不同分为多种规格。立方镜6个表面的平面度都极高,且表面中心处刻有十字刻线,精度达微米级。任意相邻面的垂直度可达±3″[2]。立方镜表面的法线可通过经纬仪、三坐标测量机等测量设备进行测量获得,利用多个面的法线便可构造立方镜坐标系。因此,航天器研制过程中,通常使用立方镜坐标系表示重要部件的空间位置。
由于装配的最后阶段只能通过测量获取到有效载荷上立方镜坐标系,而精度测量和调整的对象是有效载荷。因此在分系统装配前需要通过测量并建立立方镜坐标系及产品自身机械坐标系,从而获得立方镜坐标系与机械坐标系的关系矩阵,通常我们将此过程称为立方镜的标定。基于测量精度方面的考虑,测量范围1m以内时,立方镜的标定通常使用三坐标测量机。由于立方镜的标定结果作为航天器装配的输入条件直接影响装配精度,因此有必要对基于三坐标测量机的立方镜标定精度进行分析。而立方镜坐标系由立方镜表面法向确定,所以立方镜标定精度可以通过立方镜相邻面夹角的测量精度进行分析。
本文利用试验采样的方法,对立方镜相邻面夹角的重复性精度进行了评估。在此基础上,使用蒙特卡罗仿真法和解析法对立方镜标定的精度进行了评估。最终结合试验数据和仿真数据对基于三坐标测量机的立方镜标定给出了具体建议。
2 立方镜采样试验
以精度±5″、边长20mm的立方镜为试验对象,使用三坐标测量机测量立方镜上3个互相垂直的平面,所用型号的坐标测量机示值误差为(2.2+3L/1000)μm,20mm测量范围内,测量精度约为3μm。立方镜采样试验分为3个步骤,分别是在立方镜3个互相垂直的表面上测量4点/面、9点/面、25点/面,如表1和图1所示。每个步骤采样重复6次,试验中的采样均使用三坐标测量机的自动测量功能,重复采样使用相同的测量程序。用每个面的测点拟合平面,分别得到立方镜的面1、面2、面3,评价相邻面的夹角,以夹角的重复测量精度评判立方镜标定的重复性精度。
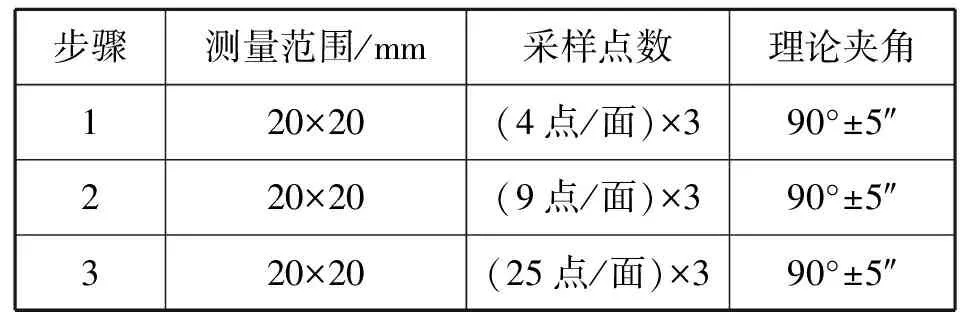
表1 立方镜采样试验Tab.1Tests with different sampling strategies of cube-mirror
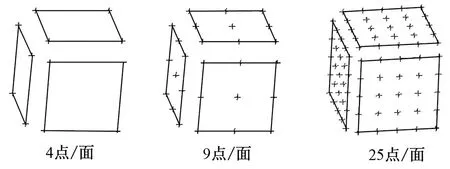
图1 立方镜采样试验Fig.1Tests with different sampling strategies of Cube-mirror
3 试验结果与分析
利用立方镜平面上测点拟合平面,计算每次采样的相邻面夹角,分别得到4点/面、9点/面、25点/面试验时面1与面2夹角、面1与面3、面2与面3夹角共3个夹角数值,如表2、表3、表4所示。从表中数据可以看出,4点/面、9点/面、25点/面试验的极差都比较大,接近8″,从实验标准差数值来看,3组试验的实验标准差相差较小,从平均值数值看,25点/面的6次采样的均值与理论值最为接近。可见,单纯从数值上难以分辨几组试验的效果,也没有规律可循。
利用表2、表3、表4中夹角数据绘制折线图,分别如图2、图3、图4所示,图中横轴为采样次数,纵轴为相邻面夹角θ数值。每幅图中有3条折线、2条虚线和3条细实线。3条折线表达立方镜3个互相垂直被测表面的3组相邻面夹角,两条虚线表达精度±5″立方镜的理论夹角区间(89.998 61°,90.001 39°),细实线表达夹角折线的平均值。从折线图可以看出,4点/面和9点/面采集测点时,3条夹角折线分布在(89.996°,90.004°)区间内,明显不能被理论夹角区间包络,且3条夹角折线的平均线只有1条在理论夹角区间内。而25点/面的3条夹角折线分布在(89.999°,90.002°)区间内,大部分能够被理论夹角区间包络,最关键的是3条夹角折线的平均线均在理论夹角区间内。
表24点/面立方镜夹角
Tab.2Thecube-mirrorangleof4points/surface(°)
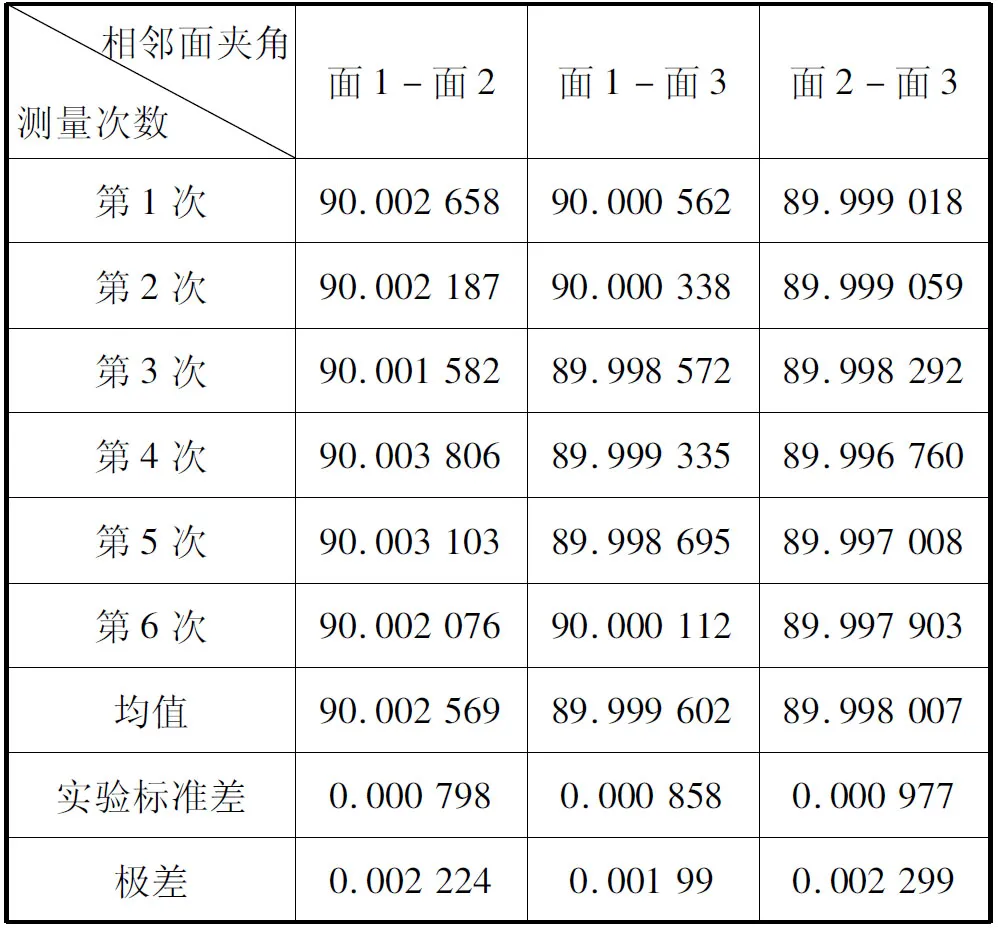
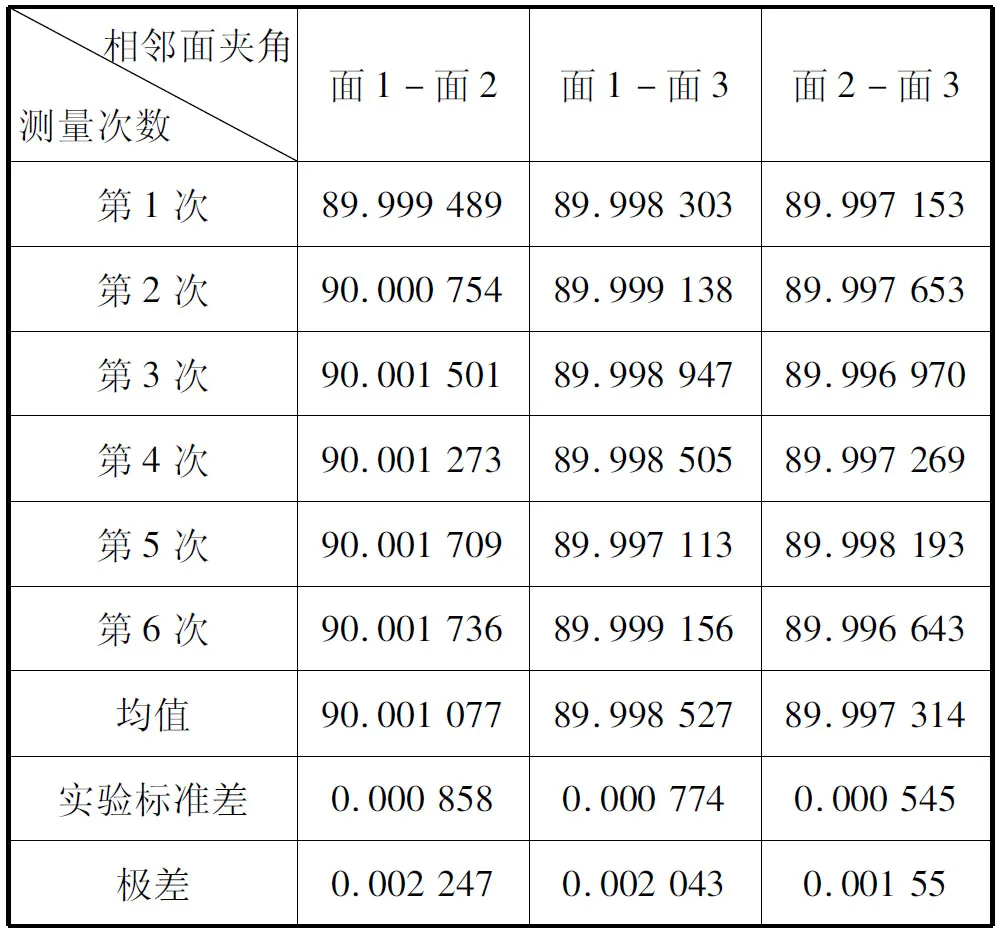
表3 9点/面立方镜夹角Tab.3 Cube-mirror angle of 9 points/surface (°)
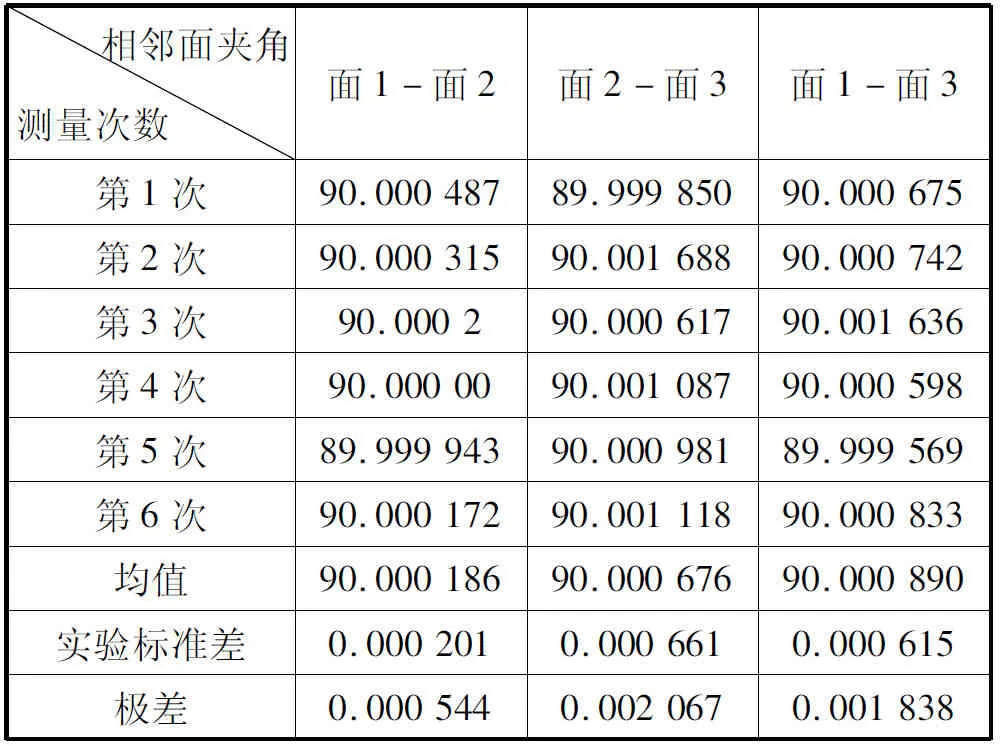
表4 25点/面立方镜夹角Tab.4 Cube-mirror angle of 25 points/surface (°)

图2 4点/面立方镜夹角Fig.2 Cube-mirror angle of 4 points/surface
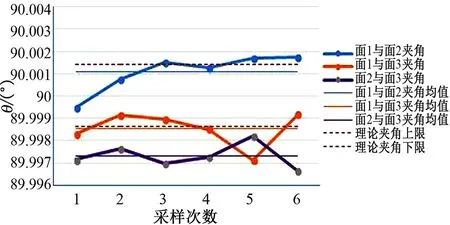
图3 9点/面立方镜夹角Fig.3 Cube-mirror angle of 9 points/surface
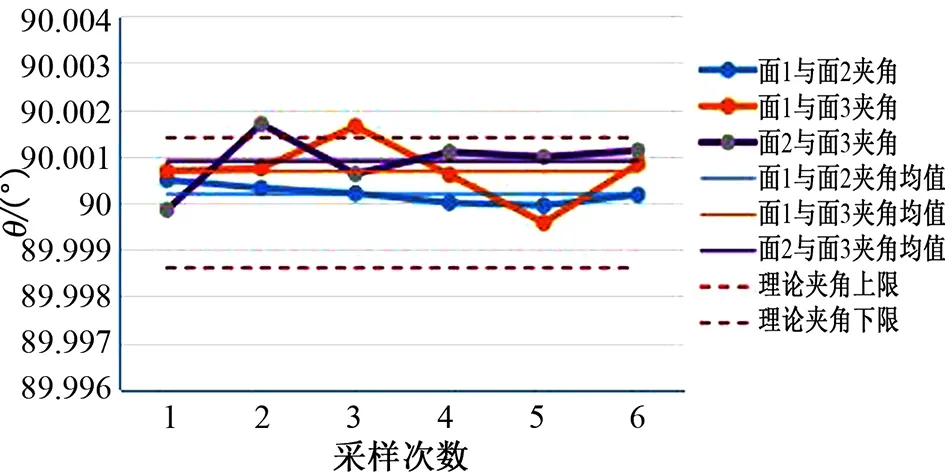
图4 25点/面立方镜夹角Fig.4 Cube-mirror angle of 25 points/surface
从3组试验数据和夹角折线图可以得出以下结果:
(1)不同采样点数的多次试验中立方镜相邻面夹角极差、实验标准差与采样点数相关性不大,其数值不会随着采样点数的增多而变小;
(2)25点/面试验的3条夹角折线大部分能够被理论夹角区间包络,而4点/面和9点/面的3条夹角折线与理论夹角区间重合区域较少;
(3)25点/面试验的3条夹角折线的平均线均在理论夹角区间内,而4点/面和9点/面的3条夹角折线的平均线只有1条在理论夹角区间内。
4 基于蒙特卡罗法的不确定度评定
从试验结果可以看出,试验得到的数值并不能充分表达立方镜夹角的测量精度。为了进一步地分析立方镜夹角测量精度,将夹角测量不确定度作为衡量立方镜标定精度的指标。测量不确定度表征合理赋予的被测量之值的分散性,是与测量结果相关联的参数,是反映测量结果是否可靠的一个重要参数[3]。测量不确定度评定主要有蒙特卡罗仿真法和GUM中的解析法。
蒙特卡罗(Monte-Carlo)仿真法,简称MCM方法,其以大数定律和中心极限定理为理论基础[4]。基于MCM方法估计夹角测量不确定度的流程[5]为:设夹角θ与测点(xi,yi,zi)的函数关系为θ=f(xi,yi,zi),利用MATLAB软件中的normrnd函数产生多维符合正态分布的随机数作为随机误差注入到测点坐标上,然后通过函数模型计算θ。相同的模拟仿真过程执行m次,就可以得到θ的m个可能的测量值,对θ={θi|i=1,2,…,m}进行统计,就可以得到θ的测量不确定度。
设立方镜相邻两个平面方程分别为
A1x+B1y+z+C1=0
(1)
A2x+B2y+z+C2=0
(2)
立方镜相邻面夹θ为
(3)
设每个测点的不确定为u0,则
uxi=uyi=uzi=u0
u0主要由测量机示值误差引起。所用型号的坐标测量机示值误差为(2.2+3L/1000)μm,立方镜测量范围为20mm,综合考虑测量重复性误差等因素,得到测量机误差约为3μm,服从正态分布,则单点测量不确定度u0=3/3=1μm。
因此,蒙特卡罗仿真时,利用MATLAB程序产生一组样本容量为1000000的随机数,且随机误差服从如下分布
σ~N(0,0.001)mm
将立方镜两个表面的25个测点/面的测点坐标作为输入,通过注入产生的随机数,得到1000000组测点坐标,每组包含25个测点。利用奇异值分解法分别计算每组测点对应的A、B等参数,再利用数学模型计算夹角θ,对1000000组的夹角θ求实验标准差,得到夹角θ的不确定度为0.002861°。为了给解析法求解夹角不确定度提供输入,计算了两个平面方程中的A、B的相关系数,分别为-0.0286和0.7632。
为了获得夹角测量不确定度与每个平面测量点数的关系,利用蒙特卡罗仿真方法计算了4个测点/面、9个测点/面、36个测点/面、49个测点/面、64个测点/面等多种情况下的各个参数的不确定度及夹角不确定度,计算数据如表5所示。
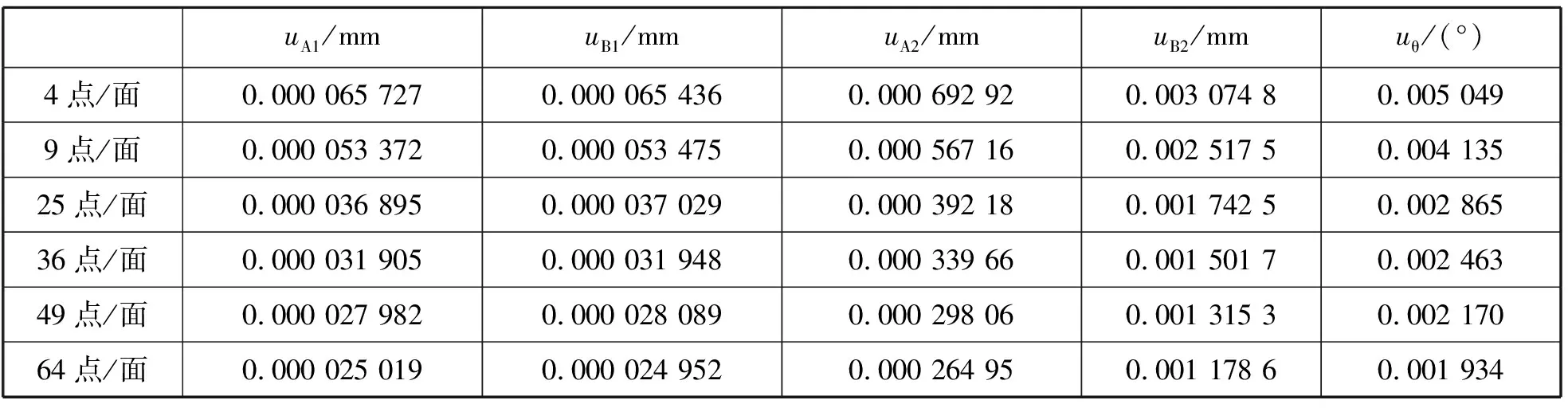
表5 不同测点数量的测量不确定度Tab.5 Measurement uncertainty of different sampling strategies
从表中数据可以看出,夹角测量不确定度随着测点数量的增加而减小,最小接近0.002 0°。但是其减幅随着测点数量增加呈减小趋势。
5 基于解析法的不确定度评定
解析法是GUM导则[6]提供的不确定度评价方法,是一种基于不确定度传播规律的方法,GUM中对不确定度的解析法评估提供了定义和标准程序。使用解析法评定测量不确定度的基础是输出量与输入量的模型。针对本文的立方镜夹角测量不确定度计算,公式(3)即是表达输出量-夹角与输入量-测点坐标的模型。由于立方镜3组相邻面夹角不确定度评价方法相同,因此以其中一组夹角(关联的两个表面与第4节计算所用的表面相同)为例,使用解析法评定夹角不确定度。
根据GUM中不确定度解析计算法,对式(3)的每个分量求偏导,可得夹角θ的不确定度uθ
(4)
式中:uA1、uA2、uB1、uB2——分别为平面方程中参数的不确定度;rA1B1——参数A1与B1之间的相关系数;rA2B2——参数A2与B2之间的相关系数。
从式(4)中可以看出,计算夹角θ的不确定度首先要确定夹角计算数学模型中A1、B1、A2、B2各参数的不确定度、传递系数及参数之间的相关系数。设测点坐标为(xi,yi,zi),则根据最小二乘原理,平面方程中的待定参数A、B、C由式(5)~式(7)确定。通常假设测点的三维坐标xi、yi、zi之间互不相关,则参数A、B的不确定度可由式(8)、式(9)求得。
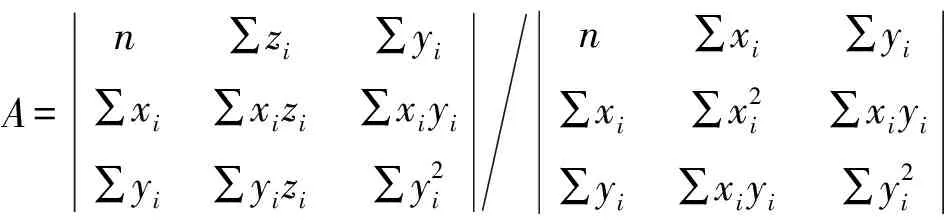
A=n∑zi∑yi∑xi∑xizi∑xiyi∑yi∑yizi∑y2in∑xi∑yi∑xi∑x2i∑xiyi∑yi∑xiyi∑y2i
(5)
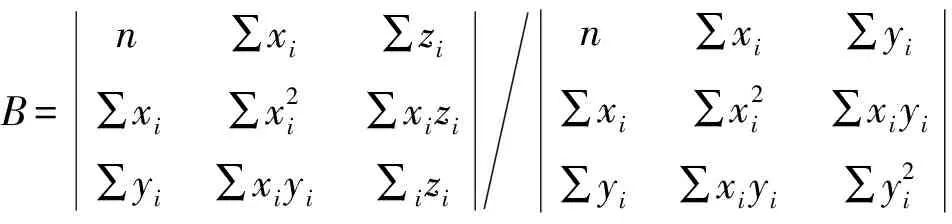
B=n∑xi∑zi∑xi∑x2i∑xizi∑yi∑xiyi∑izin∑xi∑yi∑xi∑x2i∑xiyi∑yi∑xiyi∑y2i
(6)
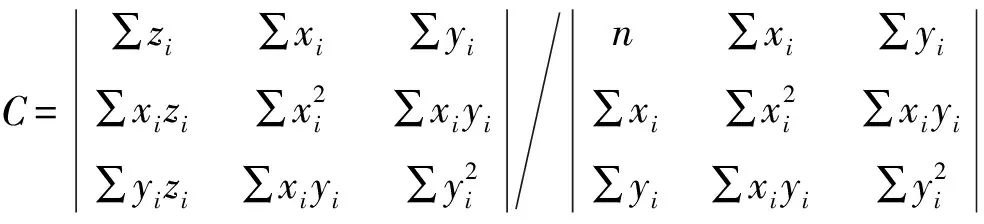
C=∑zi∑xi∑yi∑xizi∑x2i∑xiyi∑yizi∑xiyi∑y2in∑xi∑yi∑xi∑x2i∑xiyi∑yi∑xiyi∑y2i
(7)
(8)
(9)
将两个表面的25个测点/面的测点坐标及测量不确定度带入式(5)~式(9)中,可得
uA1=0.000 037 035
uB1=0.000 037 016
uA2=0.000 392 74
uB2=0.001 744 3
利用以上获得的A1、B1、A2、B2不确定度数据及第4节获得的平面方程参数间的相关系数,计算式(4),可得uθ=0.002 866°。
可见,与解析法计算求得的夹角θ的不确定度相差很微小,两种算法求得的结果一致性较高。
6 结束语
立方镜作为航天器产品的工艺基准,在航天器产品的部装和总装过程中起到了关键作用,装配前通过提前标定目标立方镜和有效载荷的关系矩阵,即可在产品装配状态下实现对不可测的有效载荷的间接测量,从而达到获得和调整有效载荷的安装位置和姿态的目的。立方镜和有效载荷的关系矩阵的标定是影响有效载荷装配精度的主要因素,分析立方镜自身的测量精度有着重要意义。本文利用立方镜夹角测量重复性试验及夹角测量不确定度的解析法和蒙特卡罗方法对立方镜测量精度进行分析,通过立方镜采样试验数据及理论方法计算得到的不确定度可以得到以下几点结论:
(1)不同采样点数的多次试验中可以看出,立方镜相邻面夹角极差、实验标准差与采样点数相关性不大,其数值不会随着采样点数的增多而变小,但25点/面试验的3条夹角折线大部分能够被理论夹角区间包络,且3条夹角折线的平均线均在理论夹角区间内;
(2)立方镜相邻面夹角的测量不确定度随着采样点的数量增多而减小,但不确定度的降幅随着采样点数的增多呈减小趋势;
(3)基于蒙特卡罗法和解析法的立方镜相邻面夹角测量不确定度评定结果相差微小,两种评定夹角测量不确定度的方法一致性较好;
(4)当利用本文提及的三坐标测量机对立方镜平面测量且采点数达到64点/面时,立方镜相邻面夹角的测量不确定度约为0.002 0°;
(5)从多次测量试验数据和理论分析获得的夹角测量不确定度可以看出,多次试验测量获得的立方镜相邻面夹角均落在90°±2uθ区间内,试验数据和理论分析结果是一致的。
基于以上数据和结论,针对航天器产品的工艺基准立方镜的测量提出以下几点建议:
(1)应首先根据立方镜标定精度指标要求评估使用三坐标测量机标定立方镜的精度是否符合指标要求;
(2)应当根据立方镜标定精度指标要求,合理选择三坐标测量机和采样方案;
(3)当大密度的立方镜平面采样点数难以实施时,应评估最少采样点数,且立方镜的采样应重复多次,以多次采样的平均值作为立方镜标定输入条件。

