建立激光跟踪仪地理坐标系与六自由度测量方法的研究

汪 涛 刘 凯 姜云翔 王 强

(北京航天计量测试技术研究所,北京 100076)

1 引 言

目前，六自由度测量主要是建立在仪器测量坐标系的基础之上，比较成熟的专业测量设备有Leica、Faro等生产的激光跟踪仪。

以Leica的AT901-LR型号为例，其点位测量与六自由度测量的主要指标如表1。

在实际工程应用中，会出现被测目标距离主机架设位置大于15m测量半径的情况：如某目标高度超过20m，需要测量目标顶部在风载条件下的晃动参数；如某目标漂浮于距离岸边50m的水面，需要测量其摇摆的参数[1]。对于上述所列举的两个应用场合，其共同特征是无法将主机架设于六自由度测量半径内。

表1 AT901-LR点位测量与六自由度测量指标对比[1]Tab.1 AT901-LR accuracy of points and 6-DOF measurement

为此研究了一种基于点位测量的六自由度测量方法，并引入当地地理坐标系作为测量坐标系。

2 测量原理

2.1 测量设备构成

基于点位测量的六自由度测量需要3套主机+靶球，其测量距离与采样频率以及测量精度与点位测量的参数一致。

在引入当地地理坐标系时，需要方位基准+经纬仪，或者使用陀螺经纬仪，与目前六自由度测量方法所需设备一致。

2.2 测量基本原理

六自由度测量是指空间位置与空间姿态测量，将一个物体看作质点时所具备空间信息为位置，以该质点建立被测轴系后，被测轴系相对外部参考空间存在的旋转量为姿态。

借助外部方位基准与经纬仪，通过下述方法的测量计算，将各台激光跟踪仪测量坐标系转换为统一的当地地理坐标系。

在被测物体上取3个不共线的测量点，按照一定规则建立出被测轴系，实时同步测量3个测量点，即可以解算出被测轴系在当地地理系坐标系下位置与姿态参数。

3 测量实现

3.1 激光跟踪仪建立地理坐标系

在被测目标的外侧架设3台激光跟踪仪与1台经纬仪，在跟踪仪、经纬仪可同时通视的区域布设4个转换点。

使用方位基准或者陀螺寻北的方式，使得经纬仪获取绝对北向方位值。使用一个靶球放置于转换点Tm(m=1,2,3,4)，经纬仪测量靶球的中心，记录靶球在当地地理坐标系下的方位角Hm(m=1,2,3,4)与俯仰角θm(m=1,2,3,4)，激光跟踪仪Gn(n=1,2,3)测量记录靶球在跟踪仪测量坐标系下的点位数据(Xnm,Ynm,Znm)(n=1,2,3,m=1,2,3,4)。

数据采集过程中，在同一个转换点，旋转靶球进行多次采集计算均值作为测量结果，减小靶球球度误差代入。

由跟踪仪测量出T1～T4四点直角坐标后，可以按公式(1)计算出T1T2、T2T3、T3T4长度

(1)

由经纬仪测量出T1～T4相对于经纬仪极坐标后，可以按公式(2)表达为直角坐标形式

(2)

可以按公式(3)计算出∠T1JT2、∠T2JT3、∠T3JT4

(3)

G1-跟踪仪；J-经纬仪；T1、T2、T3-分别为三个转换点；θ1、θ2、θ3-经纬仪分别对三个转换点的俯仰角图1 激光跟踪仪与经纬仪对转换点测量示意Fig.1 Laser tracer and theodolite measure tranformation points

如图1所示，在J-T1T2T3构成的四面体中，使用割线迭代算法[2]计算数值解，求解JT1、JT2、JT3长度。设JT1初值为经纬仪仪器高，则有公式(4)

(4)

同理,也可由T2～T4三点得到JT2、JT3、JT4的长度，由T3、T4、T1三点得到JT3、JT4、JT1的长度，将上述的结果进行均值计算后得到JT1～JT4的长度。

以跟踪仪G1为例，测量坐标系经过旋转矩阵与平移矩阵转换后得到经纬仪坐标系[3]，表达式如公式(5)

(5)

按公式(6)求差去除平移矢量

(6)

求旋转矩阵见公式(7)

(7)

求平移矢量见公式(8)

(8)

同理可以计算出另外两台激光跟踪仪的旋转矩阵R2、R3，以及平移矢量M2、M3。

3.2 多台激光跟踪仪六自由度测量

基于上述坐标系转换后，激光跟踪仪所测量的点位数据为当地地理坐标系下的输出，且多台跟踪仪与经纬仪坐标具有相同的原点。

图2 三个测量点构建直角坐标系Fig.2 Build coordinate system by three measurment points

已知某时刻A、B、C三点坐标为(XA,YA,ZA)、(XB,YB,ZB)、(XC,YC,ZC)，则O点坐标如公式(9)

(9)

(10)

计算X轴、Y轴不水平度如公式(11)

(11)

计算X轴、Y轴方位如公式(12)

(12)

式(9)、(11)、(12)即为被测轴系在当地地理坐标系下的六自由度参数。当被测轴系与被测目标存在初始偏差时，需要将被测轴系转换到被测目标的坐标系上，例如被测轴系为船体的纵、横轴，被测目标为惯导设备，本文不再细述。

4 坐标转换测试

使用一台Leica TM5100A电子经纬仪和一台Leica LTD709激光跟踪仪对上述坐标转换算法进行试验。表2为激光跟踪仪与经纬仪对转换点的测量数据；表3为单台激光跟踪仪的原始测量数据，以及采用表2数据转换为地理坐标系后的数据。

表2 转换点测量数据Tab.2 Transformation data

表3 测量数据及转换后数据Tab.3 Measurement data and transformed data mm

5 误差分析

误差来源：(1)由于经纬仪北向方位的获取属于北向传递的过程，不作分析，认为经纬仪本身能够获得无误差的北向值；(2)经纬仪与激光跟踪仪在转换坐标系时的测量误差，导致激光跟踪仪坐标系与当地地理坐标系之间存在偏差；(3)激光跟踪仪测量三个点的点位测量误差；(4)三台激光跟踪仪测量不同步引入的误差，该误差只对动态测量产生影响，且与运动速度有关；(5)解算过程中的舍入误差等其他误差。

以Leica公司T3000电子经纬仪、AT901-LR为例进行概略分析，电子经纬仪角位置测量不确定度为uc=0.5″，测角误差受目标距离的影响不考虑；激光跟踪仪的点位各分量最大测量误差为0.010mm +0.008mm/m。80m边界处两点相对距离的最大误差计算如下

(0.010mm+80m×0.008mm/m)×2=1.3mm

若测点间距离为2000mm，则两测点解算姿态时两方向合成误差为

arctan(1.3mm/2000mm)=0.037°

在动态测量过程中，受到时间不同步的影响，将造成三个测量点的相对位置变化的现象，具体误差受跟踪仪与测点的布局、运动速度等影响。图3所示为最佳的测量布局(T1～T4不共面)。

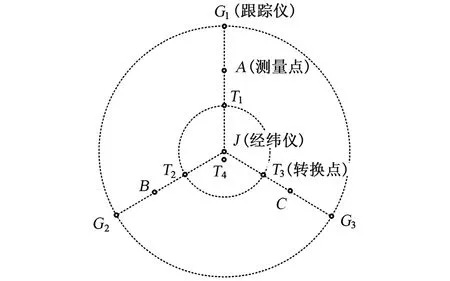
图3 转换点与经纬仪原点的相对关系图Fig.3 Transformation point and theodolite origin

6 结束语

本文所研究的测量方法，可以完成两个独立的功能，一是实现以点位测量范围进行六自由度测量，一是建立当地地理坐标系，使得所测为地理系姿态，便于惯性导航等产品测试应用。提供大范围动态六自由度测量的技术途径，其位置测量精度受坐标系转换有所降低，但其姿态测量是在点位测量的基础上得到，能够获得较高的测角精度。