机械臂运动学标定技术发展概况

谢习华 李智勇 周烜亦 张志赟 范诗萌

(1.中南大学高性能复杂制造国家重点实验室，长沙 410083;2.山河智能装备股份有限公司，长沙 410100)

1 引 言

利用机械臂对物体进行转载和定位已广泛应用于国防、工业、医疗等领域，但随着控制要求的不断提高，机械结构越加复杂，机械臂控制模型的建立以及精度计算的难度也逐渐增加。目前广泛应用的工业机器人其重复定位精度已达0.01mm[1]，但由于受零件制造误差、装配误差、负载变化等因素的影响，其绝对定位精度仍为毫米级[2]，这极大限制了机械臂在高精度装配、定位等任务中的应用。

机械臂运动学标定是一种提高机械臂定位精度的方法，它只对运动学控制模型的参数进行修改而不改变机械臂的硬件配置，因此具有良好的经济性。运动学控制模型代表了笛卡尔坐标系与机械臂关节空间之间的对应关系，控制模型的准确性直接决定了机械臂的绝对定位精度的高低，因此，如何通过标定的方法得到准确的控制模型受到国内外研究学者的广泛关注。根据标定方法的不同，运动学标定可分为基于模型的参数运动学标定、自标定和无参数运动学标定。本文针对每种标定方法的研究现状、标定特性以及存在的问题进行了总结，并探讨机械臂标定方法的发展方向。

2 基于模型的参数运动学标定

基于模型的参数运动学标定是一种建立和求解运动学误差模型的方法，实现笛卡尔空间与关节空间之间的精确转换。基于模型的参数运动学标定过程，可分为运动学建模、末端执行器姿态测量、参数辨识和误差补偿四个步骤。

2.1运动学建模

机械臂标定的运动学模型需要具有三个特点:模型的完备性、模型的连续性以及参数的最少化。基于以上三个原则，通过对现有的运动学建模方法分析，可以将其分为两大类：基于局部连杆坐标系(MLCS)的运动学标定模型和基于全局坐标系(MGCS) 的模型[3]。

基于局部连杆坐标系(MLCS)需要建立所有连杆坐标系，通过一系列相邻坐标系之间的转换实现基础坐标系和末端执行器坐标系之间的转换。MLCS方法基于DH方法，国内外学者开发了不同的建模方法，如改进的DH方法、S模型方法、CPC模型方法和MCPC模型方法。MCPC是MLCS中最先进的运动学标定方法之一，它具有完备性、连续性和非冗余参数的特点[4]。与建立DH方法的连杆坐标系相比，MCPC方法连杆坐标系的定义是任意的。

基于全局坐标系(MGCS)只需要建立基础坐标系和末端执行器的坐标系，不需要建立每个连杆的坐标系。该方法是基于零参考系模型，并根据螺旋理论发展到POE模型。POE法是利用工件坐标系和基础坐标系进行运动学建模，对建模过程进行了简化，因此具有广泛的适用性。和其他运动学建模方法相比，POE法在对连接参数修正的同时也对关节的零点进行标定，能有效的提高末端的姿态精度。王一等[6]以POE为基础建立了6自由度机器人正向运动学模型，用映射法建立空间网格，利用PSO优化的神经网络对机器人完成了标定。吴永强等[7]利用POE方法建立误差模型，对MOTOMAN-MH80机器人进行标定，使其绝对定位精度提高了80%以上。

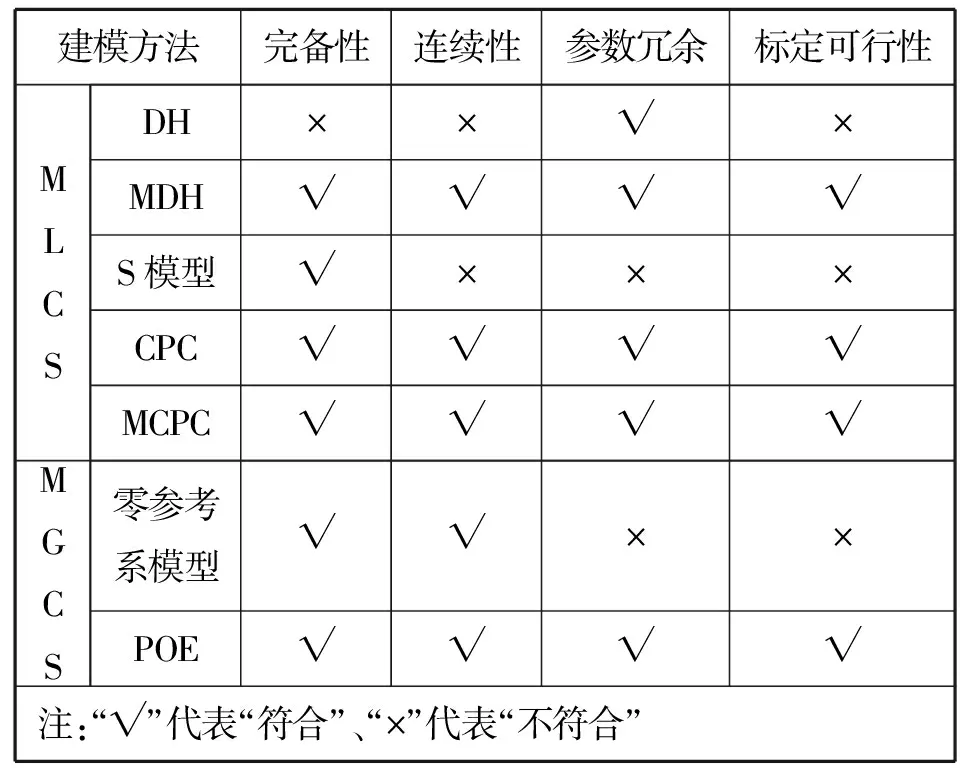
表1 各种运动学建模方法比较Tab.1 Comparison of various kinematics modeling methods

对常用的运动学建模方法进行比较，如表1所示。目前，国内大多数用于机械臂标定的运动学建模方法还是DH法，DH法只有4个连杆参数，当机械臂相邻关节轴线平行时，其在轴线方向的微小误差可能会导致在轴线的垂直方向较大变化，这些变化会导致机械臂的奇异性问题，从而导致运动学模型的不连续性。目前将MCPC法、POE法等高级运动学建模方法用于机械臂标定的还很少。

2.2末端执行器测量

在运动学标定过程中，末端执行器的姿态测量精度直接决定了标定精度。在大多数标定方法中使用外部测量设备来获得所需的信息，如三坐标测量机、激光追踪器、经纬仪、球杆仪、视觉或机械的设备，不同的测量装置有不同的测量精度。此外，每个设备的操作复杂性也不同。常用的测量设备包括:

(1)三坐标测量机

三坐标测量机(CMMS)是一种可以测量物体的几何特性的仪器，如图1所示，它可以在移动轴上安装探测器。该探头可分为机械、光学、激光等多种类型，测量精度高，可靠性高，缺点是占地面积大，成本高。张立杰等[8]利用CMMS确定球面机构的近似球心，以此为原点建立了测量坐标系，完成了球面5R并联机构的运动学标定。

图1 Heaxgon三坐标测量仪 Fig.1 Heaxgon three coordinate measuring instrument

图2 Leica激光跟踪仪Fig.2 Leica Laser Tracker

(2)激光跟踪仪

激光跟踪仪是目前最为先进的末端姿态测量设备，由于其测量精度高、测量范围大和无接触式测量等优点被广泛应用于机械臂的标定，如图2所示。Newman[9]利用激光跟踪仪对P8机器人进行标定，对其结构参数进行辨识修正，减小了31%的测量误差。但因为两方面的原因极大限制了激光跟踪仪的应用，一是激光跟踪仪是利用激光实现无接触高精度测量，因此对于激光的连续性要求较高，但在实际使用过程中激光跟踪仪很容易受各种影响而断光，从而导致测量需从头开始，降低了测量效率；二是目前激光跟踪仪产品少、价格高，配置一套标定激光跟踪仪设备需要近百万元的费用，因此对于小规模标定实验经济性差。

(3)球杆仪

球杆仪主要被用于各种机床的标定，也可用于一些自由度较低的机械臂的标定。其工作原理是利用球杆仪连接移动末端和工作台，通过测量得到的圆形轨迹与标准圆比较从而得到末端的移动精度以及误差类型，如图3所示。球杆仪测量系统操作简单、精度高且成本低，但由于其接触测量的特性，利用球杆仪的标定范围小，且不适用与多自由度机械臂的标定。

图3 REN-ISHAW球杆仪Fig.3 REN-ISHA Ballbar

图4 AVT工业摄像机Fig.4 AVT Industrial View Camera

(4)摄像机

摄像机是机器人运动学标定的一种常用测量装置，如图4所示。由于其成本低、操作简单、精度高，在工业领域得到了广泛的应用。随着相机的测量技术的成熟，越来越多的学者选择相机作为运动学校准的测量仪器。

此外，还有6D测量系统，如光学追踪器，以及6D探针。然而，这些系统的成本极大地限制了其应用，而且所提供的精度与CMMS的精度没有可比性[10]。在某些情况下，由于实验条件和设备的限制，只能获得位置数据。使用多组位置数据，可以计算姿态数据，从而实现运动学标定。

2.3参数辨识

运动学识别是根据末端执行器位姿测量值以及相应关节位置测量值来计算机器人运动学模型参数的过程。参数辨识一般是用于线性误差模型的求解，但机械臂的运动学模型参数误差是高度非线性的，因此参数辨识的结果往往存在偏差，但通过多次迭代的方法可以提高参数辨识的精度。

最小二乘法作为一种优化方法也被广泛地应用于运动学模型的参数辨识中，但由于其收敛速度慢、迭代次数多导致计算量大，因而在使用中也具有一定的局限性。扩展卡尔曼滤波法也被用于参数辨识，它是一种经典的非线性系统求解方法，能够较好的处理参数辨识中的不确定性问题，但扩展卡尔曼滤波法在辨识中容易发散，且辨识精度相对较低。广义逆法[11]将优化函数线性化，并通过计算系数矩阵的广义逆矩阵的方式求解方程，计算较为简单快捷，但需进行近似处理。罗天洪等[12]基于扩展卡尔曼滤波和配准算法对SCARA机器人进行了参数辨识和误差补偿，利用扩展卡尔曼滤波器对所有影响机器人末端轨迹精度误差因素进行综合考虑，对采集的数据进行滤波，避免了采集数据的误差。Renders[13]在运动学参数识别中应用了一种参数估计方法：极大似然估计法。白云飞等[14]针对运动学模型参数辨识过程中存在的参数不连续和计算收敛速度慢的问题，利用公差限制参数的范围，准确快速地完成了对6参数模型的6R机器人的参数辨识。R.Furutain等[15]利用装有多个标准球的金属板对关节式坐标测量机进行运动学参数辨识。

2.4误差补偿

机械臂运动学标定的目标是实现误差补偿，误差补偿是利用高精度测量工具的测量数据对运动学模型中的参数偏差进行修正。由于机械臂的定位精度受多种误差因素的影响，因此其误差补偿算法也不相同。广泛应用的误差补偿算法主要有以下几种[16]：

(1)基于微分算法的定位误差补偿方法：通过微分变换将机械臂的目标姿态向与误差相反的方向进行特定的微分变换，重新计算得到机器人的名义位姿，最后求取名义位姿下的运动学逆解，得到工业机器人实际的连杆参数。

(2)基于N-R算法的定位误差补偿方法：核心思想是利用N-R算法迭代求解工业机器人关节角的补偿角度，最终将得到的关节补偿角作用于机器人控制器，以实现对机器人的定位误差补偿。

(3)基于相邻位姿误差的空间插值算法进行定位误差补偿：将给定的样本点按特定的规划方法，在一定的区间内分割为若干网格点，首先进行区域误差补偿，最终采用插值拟合的算法对彼此相邻的网格点乃至整个区间进行误差补偿，实现对机器人末端位姿的校正。

3 自标定

基于模型的参数标定和无参数标定方法对测量的数据具有很强的依赖性，数据的准确性对标定结果具有显著的影响，因此要有较好的标定效果必须使用高精度的测量设备，但此类设备一般较为昂贵，而且使用环境有一定的要求，以空间机器人为例，在无重力情况下，地面上常用的测量设备由于失效等问题而无法使用。

针对上述提到的问题，重点研究自动测量和自主计算的问题，提出了自标定方法，自标定也称为闭环标定。目前主要采用的自标定方式有两种：一种是基于物理约束的自标定；一种是利用视觉实现机械臂自标定。

3.1基于物理约束的标定方法

施加物理约束主要是通过在末端执行器上安装一个探针，机械臂在操作空间运动，只有当探测器的前端接触到约束平面时，才会记录下机械臂的关节读数和笛卡尔坐标值。通过一系列与约束平面有关的数据进行求反，可以计算出机械臂的运动学参数。这个过程中，既不需要外部传感器测量，也不需要人为干预，完全通过机械臂的自主测量和自主计算完成标定。Joubair[17]还对方法进行了优化，在约束平面的基础上还加入了距离约束，利用一个安装了3个直径300mm球体的三角板来采集数据，对FANUC-200iC机器人进行了标定，如图5所示，成功将机械臂绝对定位误差从0.698mm缩小到0.086mm。

图5 FANUC-200iC机器人自标定实验Fig.5 FANUC-200iC robot self-calibration experiment

3.2基于视觉的标定方法

随着硬件技术和图像处理技术的高速发展，机器视觉被广泛应用于各个行业，其中视觉测量也是一大研究热点，利用视觉测量具有非接触式测量和速度快等优点。根据摄像机安装位置的不同，可以将视觉标定分为手眼标定和固定视觉系统标定。手眼标定是将摄像机安装在机械臂末端，随末端执行器一起运动，而固定视觉系统标定是将摄像机安装在空间一固定位置，其位置不随机械臂运动而改变。比如， Kavita Ravi[18]等人在机械臂的末端安装摄像机，通过处理采集的图像获取机械臂的关节角度信息，从而完成机械臂的运动学参数标定，如图6所示。

图6 基于视觉的手眼标定系统Fig.6 Visual hand-eye calibration system

而固定视觉系统标定是将摄像机安装在空间一固定位置，其位置不随机械臂运动而改变。比如L.Richter等[19]将红外相机固定在三角架上，在机械臂上设置标记点，由相机得到标记点的位移，利用最小二乘法进行参数辨识，实现机器人标定。Nicolas等[20]利用相机作为外部视觉传感器，将标定板固定在6轴并联机器人平台上，完成了对机器人标定并减少了运动学参数的数量，如图7所示。

图7 固定视觉标定系统Fig.7 Fixed visual calibration system

然而，与其他复杂的测量设备相比，在覆盖较大的工作空间时，相机获得的测量数据精度较低。

4 无参数运动学标定

基于模型的运动学标定可以得到精确的运动学参数，从而得到准确的正运动学模型和逆运动学模型。运动学参数的标定是运动学标定的中间过程，国外一些学者提出了一些不考虑运动学参数的运动学标定方法。在笛卡尔空间中补偿末端执行器位置的正运动学标定，以及在关节空间中补偿关节变量的逆运动学标定，它们被统称为非参数运动学标定。同时，由于基于模型的运动学标定方法的复杂性，通过开发无参数误差模型来近似误差而不是直接建模是一种很好的方法。下面详细介绍用于建立误差映射关系的各种算法。

4.1插值

双线性插值作为一种常用的插值方法，在机器人非参数运动学标定中得到了广泛的应用。双线性插值法的应用是建立在末端位置误差为均匀分布的情况下，但实际过程中是不存在的，从而导致利用双线性插值法得到的映射关系函数不太准确，补偿精度较低。为了解决这一问题，王胜千[21]将模糊理论引入到插值方法中，通过建立控制表来存储预先定义好的输入-输出关系，根据控制表设计一模糊逻辑控制器，从而 实现模糊离线插值。Bai Y等[22]对各种插值方法进行了比较研究，如双线性、三次样条和模糊误差插值技术。仿真结果表明，采用模糊误差插值技术与双线性和三次样条相比较，可以得到更准确的补偿结果。

由于末端执行器的位置误差在模糊插值中作为输入，采用模糊插值法进行补偿的精度仍然较低。此外，构建一个模糊插值的查询表需要花费很长时间和大量存储空间。为了克服这一缺点，Bai Y[23]提出了一种新的在线模糊插值方法，通过与传统的基于模型的离线插值方法比较，在相对紧凑的工作空间中，其精度和对复杂模型的适用性方面都优于传统的离线模糊插值方法。

4.2神经网络

算法随着计算机技术的提高已发展得相当成熟，包括神经网络、模糊逻辑和遗传算法等，已广泛应用于各行业。机器人控制系统通常是高度非线性和多耦合的复杂系统，它们精确的运动控制模型很难获得。神经网络可以通过调节参数不断逼近复杂的非线性函数，因此利用神经网络来进行非参数运动学标定是一种可行的标定方法。

神经网络建立的模型可以考虑机械臂末端执行器位置误差的所有因素[24]。基于模型的运动学标定方法的优点是可以量化误差因素的权重，但并不是所有误差因素都能反映在误差模型中，然而神经网络很擅长处理这类问题。利用神经网络处理标定问题有两种方式：

一种是直接利用神经网络建立末端执行器实际位置与关节角度之间的关系，实现关节角度空间到笛卡尔坐标系空间的直接转换，如图8所示。该方法无需建立机械臂的运动学模型，能够避免机械臂自身参数误差对定位精度的影响，从而简化了标定过程，但此种方法需要大量的实验数据，机械臂在未投入工作前很难获取大量的数据。而且神经网络对数据的依赖很强，网络训练的好坏与训练数据有直接的关系。因此，如何在数据量有限的情况下能够获得较好的训练效果成为广泛研究的热点。

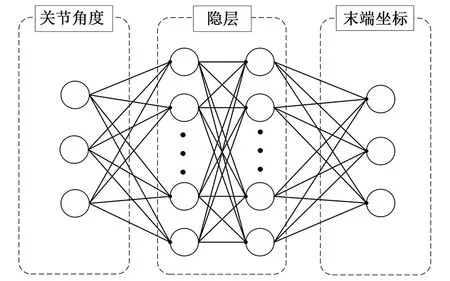
图8 神经网络直接标定Fig.8 Direct calibration based on neural network

另一种是利用神经网络得到机械臂控制的误差模型，再结合运动学模型得到实际控制模型。当神经网络与运动学正解结合用于正运动学标定时，期望的坐标位置是作为神经网络的输入，经过训练的神经网络模型可以得到期望位置与实际位置的误差，从而得到实际的位置坐标，如图9所示。

图9 神经网络正运动学标定Fig.9 Forward kinematics calibration based on neural network

当神经网络与运动学逆解结合用于逆运动学标定时，理论关节变量是作为神经网络的输入，经过训练的神经网络模型可以得到关节变量误差，从而得到实际关节变量，如图10所示。根据神经网络所使用的条件，确定输入层和隐藏层的节点数。王战中等[25]利用基于神经网络的机器人逆运动学标定法对一6自由度机器人进行了标定，并利用遗传算法优化了神经网络的权值与阈值，结果证明该方法可以进一步提高标定精度。

图10 神经网络逆运动学标定Fig.10 Inverse kinematics calibration based on neural network

机械臂在未投入工作前很难获取大量的数据。而且神经网络对数据的依赖很强，网络训练的好坏与训练数据有直接的关系[26]。因此，如何在数据量有限的情况下能够获得较好的训练效果成为广泛研究的热点。

对以上各种机械臂运动学标定方法进行比较，如表2所示。

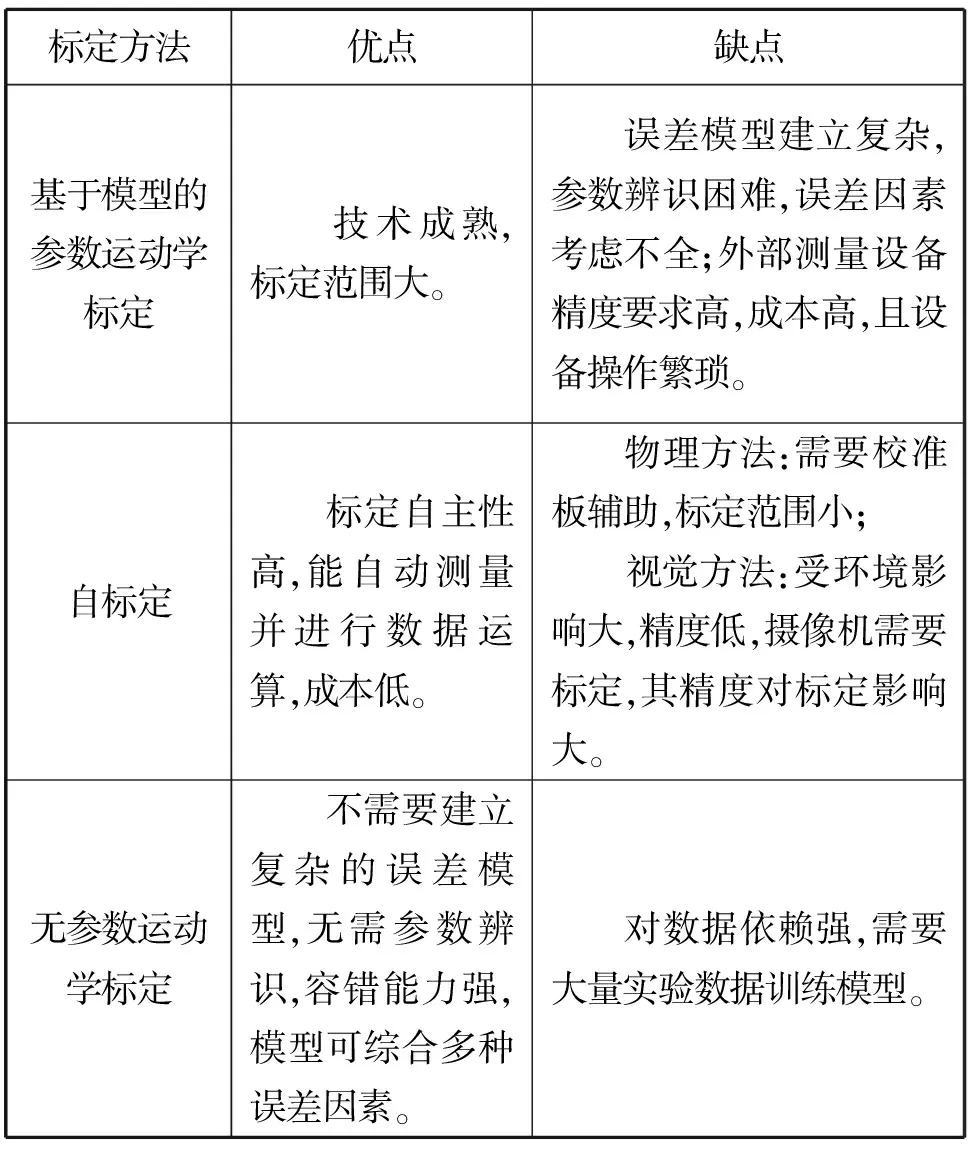
表2 机械臂各种运动学标定方法比较Tab.2 Comparison of various kinematics calibration methods of manipulator

5 结束语

到目前为止，国内外诸多学者对运动学标定进行了大量研究，并取得了许多研究成果，部分研究成果已成功应用于机器人标定。然而，在运动学标定中仍存在许多问题，有待进一步研究和探讨。

5.1 对于基于模型的运动学参数标定，在建立误差模型的过程中，经常忽略或假定传感器的关节角误差。然而，在实际应用中，由于传感器精度的问题，关节角测量的误差对运动学参数误差有较大的影响。因此，如何将关节角测量误差引入到运动学参数标定模型中，建立一个完整的运动学误差模型，需要进一步研究。

5.2 在机器人运动学参数标定过程中，由于重力效应，连杆会变形，特别是对于具有较大跨度的机器人，它将产生关节传动系统的扭转变形。由于在测量过程中每个角度都是不同的，因此由重力和重力转矩引起的变形也不一样，这给运动学参数的标定带来了随机性。因此，如何采取有效措施消除重力和重力转矩对运动学参数标定的影响是非常重要的。

5.3 对于现有的自标定技术，其工作空间受校准板的限制。同时，校准板的加工精度和算法的迭代精度对运动学标定精度有很大的影响。为了扩大自标定的应用，可以用数字电子校准板代替传统校准板，也可以避免标准单位网格点的加工误差对校准精度的影响。另外，现有的标定方法非常复杂，计算复杂度高，处理时间长，因此实时校准和快速校准是进一步的研究趋势。

5.4 各种机器人与机械臂越来越多应用于各个行业，其运动学精度的要求也越来越高，因此机械臂运动学的实时标定成为未来的研究趋势。神经网络作为一种智能算法，不仅可以精确地逼近任意连续非线性函数，而且具有很强的鲁棒性和独立学习能力，为网络自适应重建提供了方便。视觉作为一种简单的测量方法，能够实时的得到机械臂任意时刻的末端位置，同时也能证明机器人的高度自适应。随着神经网络收敛效率的提高和视觉测量系统精度的提高，该组合在自适应和实时方面具有相当大的优势，将成为未来机器人运动学标定的主要研究趋势。