中低速磁浮轨道不平顺检测算法及其仿真计算*

杨 铭 林国斌 毕 晟

(1. 同济大学道路与交通工程教育部重点实验室， 201804， 上海； 2. 同济大学磁浮交通工程技术研究中心，201804，上海；3. 中国民航工程咨询公司， 101300， 北京//第一作者，硕士研究生)

中低速磁浮的轨道状态对列车运行的安全性和舒适性有很大影响[1]，因此，需要对轨道的状态进行及时的监测和维护。由于中低速磁浮F型轨道和传统轨道交通工字型轨道形面相比差异较大，因此传统轨道交通的轨道检测设备不能满足中低速磁浮的轨道检测要求。此外，用于轨道施工验收阶段的测量方法一般需要较长时间，而且精度得不到保证，因此有必要寻找适合中低速磁浮轨道不平顺检测的方法[2]。

1 中低速磁浮轨道不平顺

中低速磁浮轨道不平顺是指在轨道悬浮检测面沿列车运行方向的高低变化[3]。中低速磁浮轨道不平顺将使列车运行过程中悬浮传感器检测的间隙和加速度数值不断波动，从而引起列车垂向振动。由于悬浮间隙范围仅为0～16 mm，垂向振动幅度超过此范围时，将导致悬浮架与轨道之间接触，影响列车运行的安全性和舒适性。

不同于传统轨道交通，中低速磁浮列车1节车厢具有相对独立的5个悬浮架，轨道不平顺对列车运行舒适性的影响主要体现在对于1个悬浮架的作用，因此在1个悬浮架范围(2.8 m)内的轨道不平顺对列车运行的舒适性尤为重要。

1.1 轨排不平顺

中低速磁浮轨排不平顺主要体现在1个悬浮架范围内的轨道单点高低变化和轨道连续高低变化。其中,轨道单点高低变化是某1根轨枕处轨道明显高于或低于周围轨道高度，这是由轨道1根轨枕发生高低变化而导致的轨道不平顺；轨道连续高低变化是在某两根轨枕之间的轨道存在高低变化，而轨枕两侧的高度分别与这两根轨枕的高度相当。

1.2 轨道接缝错台

轨道接缝(以下简称“轨缝”)错台是指：由于两个轨道梁的轨面不在同一高度而在轨道接缝处产生的垂向高低差[4]。轨缝错台的危害在于使垂向出现突变的偏差，对中低速磁浮列车运行的舒适性和安全性有着重要影响。

1.3 轨缝折角

轨缝折角是指轨缝两侧的轨道线型不处于同一角度时存在的折角偏差。其危害在于使轨道之间角度发生突变，导致列车运行颠簸和晃动。

2 中低速磁浮轨道动态监测评价算法

中低速磁浮轨道动态监测评价算法是基于同一悬浮架同一侧的2个悬浮传感器的4个间隙检测探头采集的悬浮间隙数据，通过对4组间隙数据的计算和分析，来监测车辆悬浮架范围内的线路轨道不平顺。图1为中低速磁浮轨道间隙传感器位置关系图。图1中，4个间隙检测探头分别安装在2个悬浮传感器上，2个悬浮传感器分别沿轨道运动方向安装于悬浮架的两端。一组间隙传感器探头间距为d，两组间隙传感器探头间距为L。

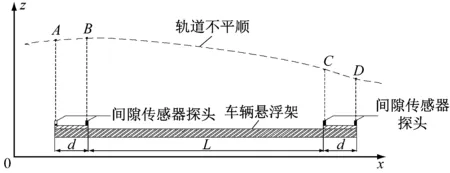
注：A、B、C、D表示4个间隙测点

图1 中低速磁浮轨道间隙传感器位置关系示意图

2.1 四点直线度计算

四点直线度监测示意如图2所示。图2中，针对4个间隙测点相对对于悬浮架的坐标A(x1,z1)、B(x2,z2)、C(x3,z3) 、D(x4,z4)，采用最小二乘法拟合获取同一时刻4个间隙测点的第一拟合直线，再根据4个间隙测点与对应拟合直线的偏差值获取中低速磁浮轨道在当前时刻所处位置的四点直线度。

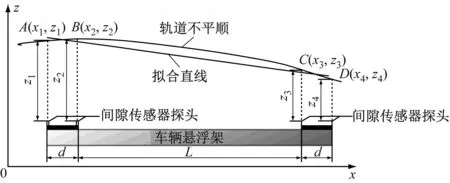
图2 四点直线度监测示意图

图2中，4个测点连线为轨道不平顺示意曲线。设4个间隙测点通过最小二乘法拟合的直线为：

z=k1x+b1

(1)

式中：

x，z——分别表示拟合直线的横坐标和纵坐标；

k1，b1——分别表示A、B、C、D四测点拟合直线的斜率和截距。

令:

(2)

式中：

Dmin——多项式的最小值；

i——间隙传感器的编号；

zi——i点的纵坐标；

xi——i点的横坐标。

根据式(1)，可求出拟合直线的斜率和截距：

(3)

(4)

然后求得z方向上的偏差值Ei：

Ei=zi-k1xi-b1

(5)

平面直线度误差为：

f=|Emax-Emin|

(6)

式中：

Emax，Emin——分别表示最大偏差值和最小偏差值。

2.2 轨缝错台计算

通过间隙值的突变来判断轨道之间的缝隙大小。悬浮架上的4个间隙传感器探头将依次通过轨缝，在第一个传感器探头通过轨缝且第二个传感器探头还未通过轨缝时，4个间隙测点相对对于悬浮架的坐标分别为A0(x1,z1)、B0(x2,z2)、C0(x3,z3)、D0(x4,z4)(见图3)。设A、B、C三点通过最小二乘法拟合的直线方程为z=k2x+b2，在D点处，计算z方向与拟合直线的偏差即为轨缝错台值：

O=z4-(k2x4+b2)

(7)

式中:

O——轨缝错台值；

k2，b2——分别表示A、B、C三测点拟合直线的斜率和截距。

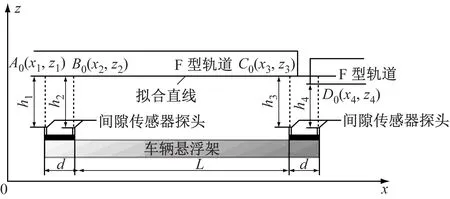
图3 轨缝错台监测示意图

2.3 轨缝折角计算

与轨缝错台监测的原理相似，通过间隙值的突变来判断轨道之间的缝隙大小。悬浮架上的4个间隙传感器探头将依次通过轨缝，若当前时刻为第三个间隙传感器探头通过轨缝且第二个间隙传感器探头未通过轨缝的时刻，则分别获取当前时刻前两个间隙测点和后两个间隙测点相对于悬浮架的坐标，前两个测点所成的直线与后两个测点所成的直线相交的锐角即为轨缝处的折角偏差。

前两个测点A、B相对于车辆悬浮架的坐标分别为(x1,z1)、(x2,z2)。通过A、B两点做直线，得到：

z=k3x+b3

(8)

(9)

式中：

k3，b3——分别表示A、B两测点拟合直线的斜率和截距。

后两个测点C、D相对于车辆悬浮架的坐标分别为 (x3,z3) 、 (x4,z4)。通过C、D两点做直线，同理可得直线方程：

z=k4x+b4

(10)

k4,b4——分别表示C、D两测点拟合直线的斜率和截距。

则轨缝折角值为两直线所夹锐角θ：

θ=arctank3-arctank4

(11)

2.4 中低速磁浮轨道动态监测算法的适应性分析

悬浮架自身刚度很大，悬浮架的在xoz平面内运动形式为沿z向上下变化(移动值为b)以及与x轴产生倾角θ。

对于悬浮架在列车运行过程中几何方位不断变化下的测量，通过如下两种情况进行比较分析。第一种情况为：在同一位置时，悬浮架保持水平姿态进行测量，此时4个测量点的坐标分别A(x1,z1)、B(x2,z2)、C(x3,z3)、D(x4,z4)。第二种情况为：在水平状态的基础上，沿z向移动b，并绕Y轴旋转θ，此时4个测量点的坐标分别为Am(x1,m,z1,m)、Bm(x2,m,z2,m)、Cm(x3,m,z3,m)、Dm(x4,m,z4,m)。

相对于水平状态，在运动状态下，对x坐标和z坐标分别进行转换，得到：

(12)

在四点直线度计算过程中，水平状态下四点拟合直线斜率为ki，截距为bi，偏差值为Ei，直线度为f；运动状态下四点拟合直线斜率为ki,m，截距为bi,m,偏差值为Ei,m，直线度为fm。

运动状态下四点拟合直线斜率为：

(13)

由式(11)～(13)，可得：

ki，m=ki

(14)

运动状态下四点拟合直线截距为：

(15)

由式(11)～(15)，可得：

bi，m=cosθ·bi

(16)

运动状态下四点偏差值为：

Ei，m=cosθ·Ei,i=1,2,3,4

(17)

运动状态下四点直线度为：

fm=cosθ·f

(18)

式中：

f——水平状态下的直线度；

fm——运动状态下的直线度。

同理，监测轨道错台值时，水平状态下三点拟合直线斜率为k2，截距为b2，错台值为O；运动状态下三点拟合直线斜率为k2，m，截距为b2,m，错台值为Om。

将Am、Bm、Cm三点拟合直线方程，如下所示：

zm=k2,mxm+b2,m

(19)

运动状态下错台值为：

Om=O·cosθ

(20)

同理，监测轨道折角值时，水平状态下A、B两点拟合直线斜率为k3，C、D两点拟合直线斜率为k4，折角值为δ；运动状态下A、B两点拟合直线斜率为k3，m，C、D两点拟合直线斜率为k4,m，折角值为δm。具体如下所示：

k3，m=k3

(21)

k4，m=k4

(22)

δm=k3，m-k4，m=k3-k4=δ

(23)

其中，将悬浮架沿z向移动b，受结构约束，波动范围为0～16 mm，倾角正切值tanθ为：

(24)

式中：

Δh——悬浮架两端间隙差(取-16～16 mm)；

Lx——悬浮架长度(取2.8 m)。

tanθ取值范围为-0.005 71～+0.005 71，对应cosθ取值范围为0.999 98～1，最大误差约为1/50 000。该值远小于悬浮控制传感器测量精度(精度为量程的1%)。因此，悬浮架因倾角产生的误差对整个动态检测的影响可忽略，即认为cosθ≈1。同时，计算过程中，沿z向移动值b在四点间隙值可以相互抵消，指标值不收沿z向移动值b的影响。基于以上分析，充分证明了动态监测评价算法的适应性。

3 中低速磁浮轨道动态监测评价算法仿真

3.1 轨道不平顺的仿真

对于悬浮架，本文前述已对中低速磁浮轨道动态监测方法的适应性分析进行了论证，悬浮架的姿态对由4个间隙测点测量的轨道不平顺指标无影响。因此在仿真过程中，可忽略悬浮架的动态变化。

3.2 轨道单点高低变化的仿真计算

在轨道单点高低变化的仿真计算中，首先模拟在3根轨枕范围，即3 m内中间轨枕高低发生的变化。在悬浮架采集的4路间隙信号中取两端的间隙信号2、间隙信号3进行分析，并根据4路信号计算求得直线度。

图4为轨道单点高低变化仿真。由图4可知，在3根轨枕范围内，轨道单点高低变化对轨道直线度具有显著影响。由于悬浮架长度为2.8 m，略小于3根轨枕的长度，存在4个监测探头均监测直线位置的情况，此时直线度为0。

a) 轨道不平顺

b) 间隙信号2

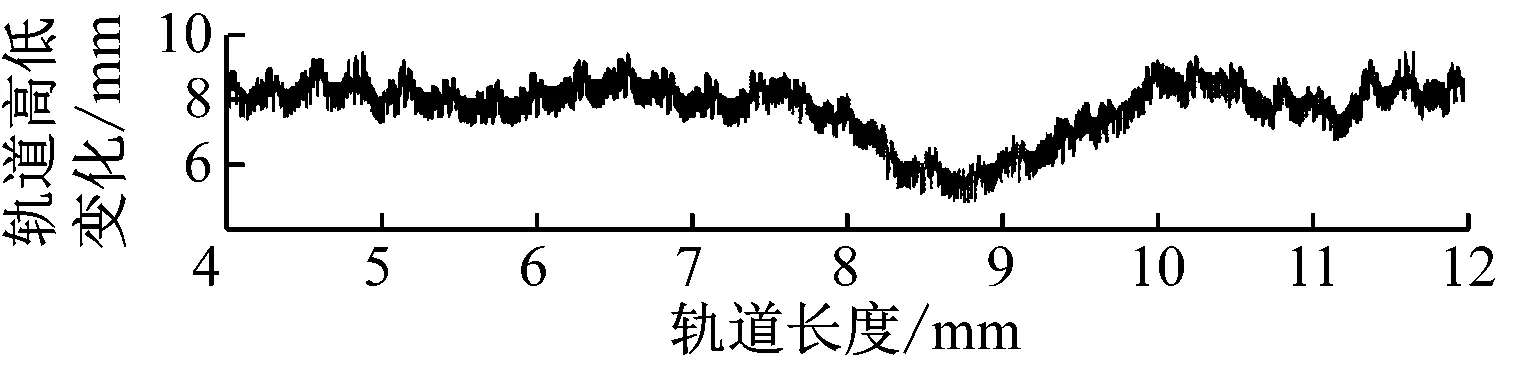
c) 间隙信号3

d) 直线度

3.3 轨道连续高低变化的仿真计算

在轨道连续高低变化的仿真计算中，需模拟在4根轨枕范围，即4.5 m内中间两根轨枕之间高低发生的变化。与轨道单点高低变化的仿真类似，在悬浮架采集的4路间隙信号中取两端的间隙信号2、3进行分析，并根据4路信号计算求得直线度。

图5为轨道连续高低变化仿真。由图5可知，在4根轨枕范围，即4.5 m内，轨道连续高低变化对轨道直线度具有显著影响。在前两个监测探头刚进入轨道连续高低变化区域和后两个监测探头临离开轨道连续高低变化区域时，直线度达到峰值。

a) 轨道不平顺

b) 间隙信号2

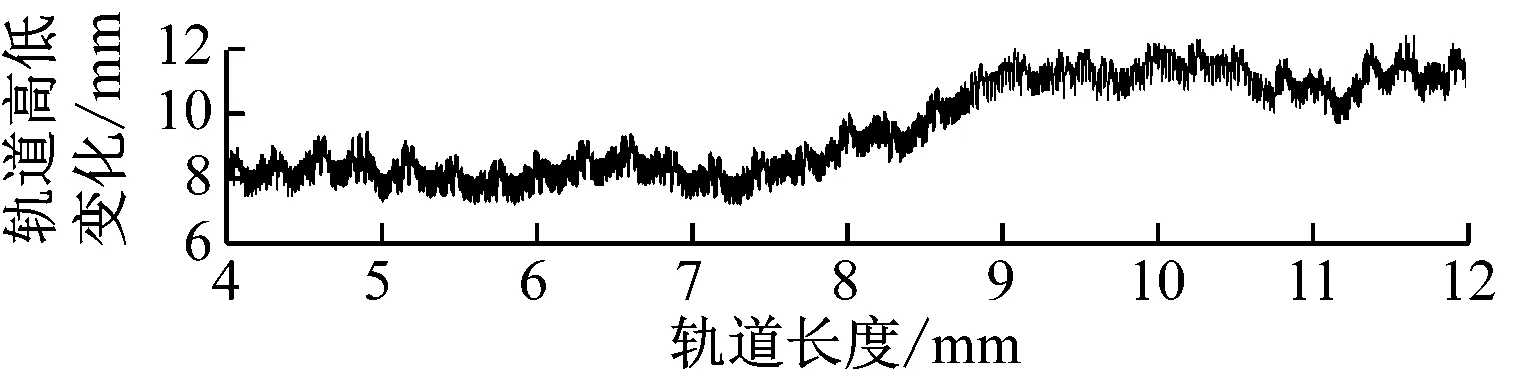
c) 间隙信号3

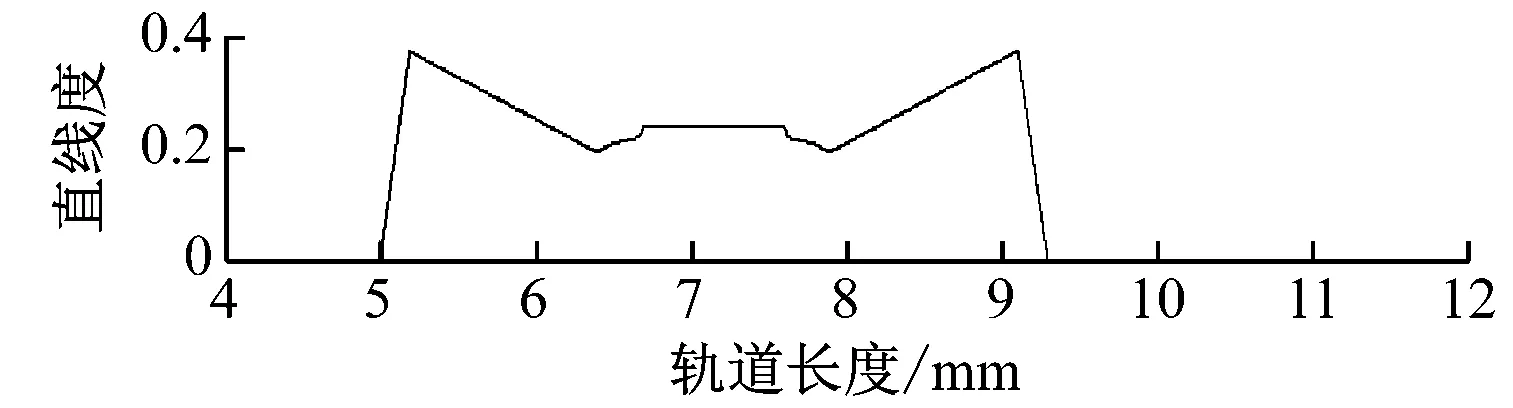
d) 直线度

3.4 轨缝错台的仿真计算

由于轨缝错台值主要通过第一个测点(间隙信号4)与其他3个测点比较计算得到，因此在悬浮架采集的4路间隙信号中取两端的间隙信号4进行分析。由图6的轨缝错台变化仿真图可知，间隙信号4基本反映了轨道错台情况，通过错台值能够准确表示高低突变。由于监测探头3、4之间有一定距离，因此错台值出现一段平台。

3.5 轨缝折角的仿真计算

在悬浮架采集的4路间隙信号中取两端的间隙信号2、间隙信号3进行分析，并根据4路信号计算求得折角。由图7的轨缝折角变化仿真图可知：悬浮架通过轨缝折角过程中，首先，前两个监测探头进入折角区段，折角值先变为负值；接着，后两个探头进入折角区段后，折角值归零；而后，前两个探头通过轨缝，进入折角反向区段，折角值达到峰值；最后，随着后两个探头、前两个探头离开折角区段，折角值依次归零、变负、归零。

a) 轨道不平顺

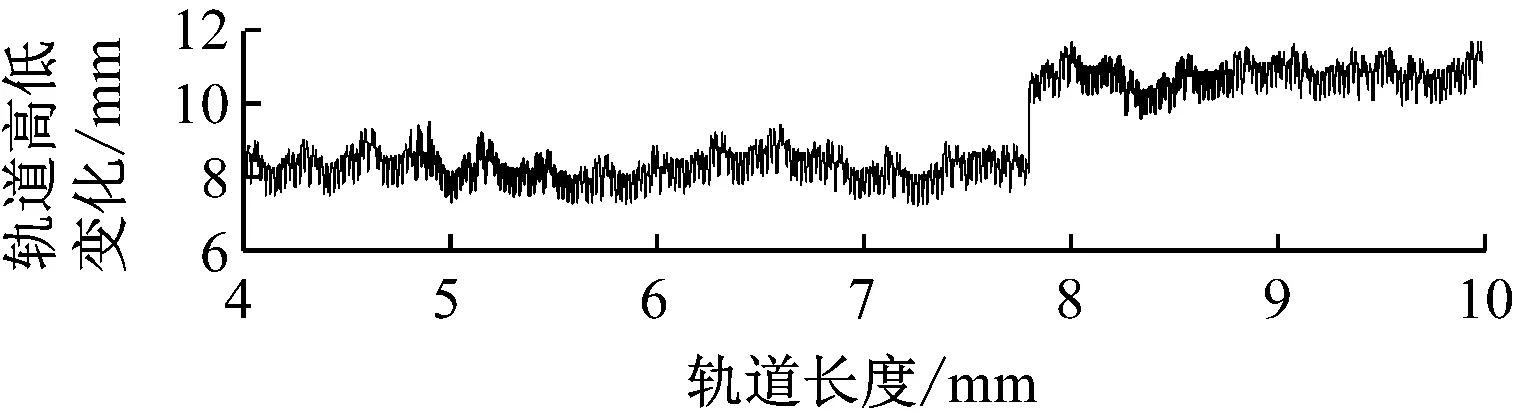
b) 间隙信号4

c) 轨缝错台变化

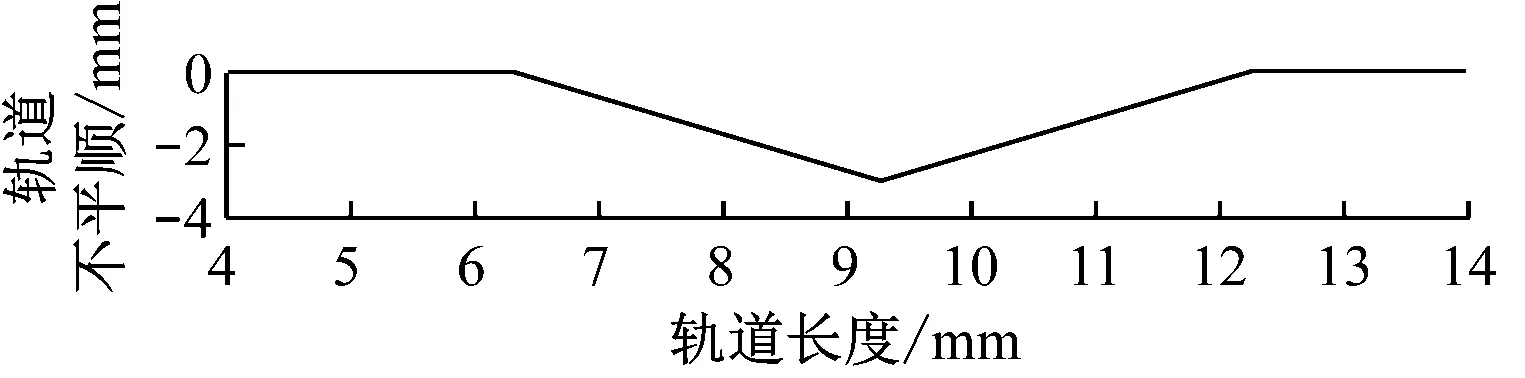
a) 轨道不平顺

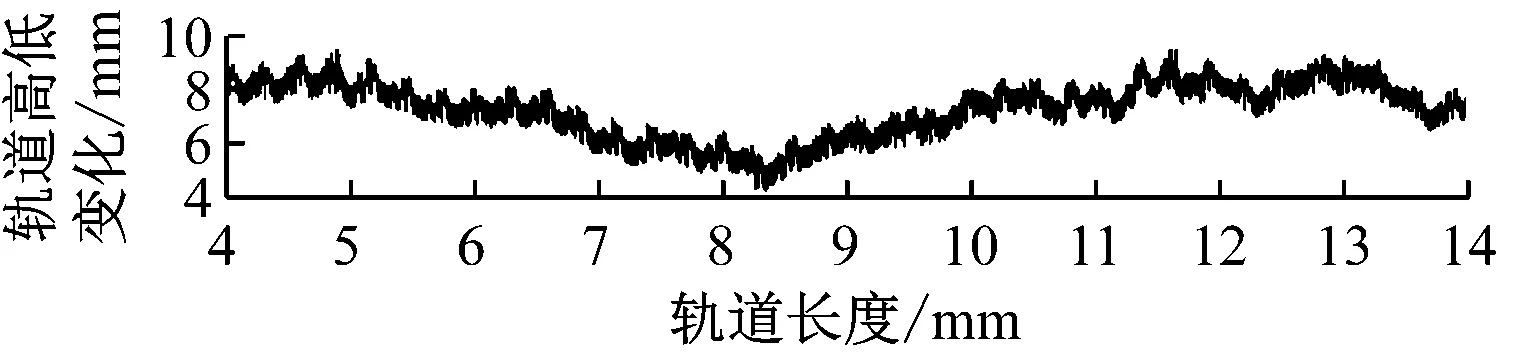
b) 间隙信号2

c) 间隙信号3

d) 轨缝折角

3.6 仿真结果分析

模拟3根轨枕范围内轨道单点高低变化值分别为1 mm、1.5 mm、2 mm、2.5 mm、3 mm、3.5 mm、4 mm时相应的轨道四点直线度；模拟4根轨枕范围内轨道连续高低变化值分别为1 mm、1.5 mm、2 mm、2.5 mm、3 mm、3.5 mm、4 mm时相应轨道的四点直线度；模拟轨缝错台不平顺值分别为1 mm、1.5 mm、2 mm、2.5 mm、3 mm、3.5 mm、4 mm时相应轨道错台指标值；模拟轨枕6 m范围内，轨缝两端折角变化值分别为1×10-3rad、1.5×10-3rad、2×10-3rad、2.5×10-3rad、3×10-3rad、3.5×10-3rad、4×10-3rad时相应轨缝折角指标值。由图8可知，轨道不平顺仿真值与轨道不平顺指标值具有较高的线性关系，可作为测量指标值和轨道实际不平顺相关性的参考。轨道四点直线度、轨缝错台指标值、轨缝折角指标值这三种轨道不平顺指标能够反映轨道不平顺的实际情况。

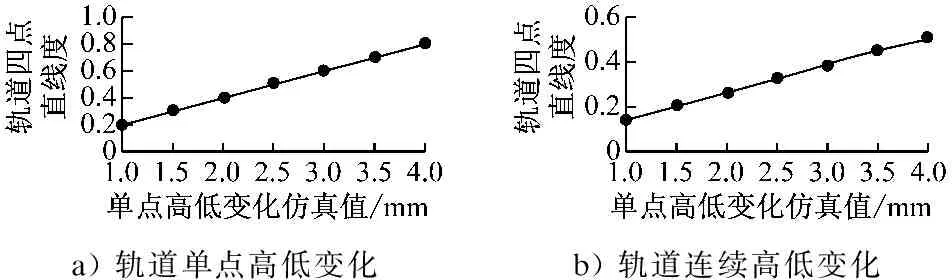
a) 轨道单点高低变化b) 轨道连续高低变化

c) 轨缝错台d) 轨缝折角

图8 仿真结果分析图

4 结论

(1) 该检测算法基于中低速磁浮列车上的悬浮控制传感器和加速度传感器，简化了检测设备，能够满足高效、便捷的要求。

(2) 对悬浮架倾斜产生的误差进行了分析，结果表明该误差对动态检测的影响可忽略。

(3) 从仿真结果可以看出，仿真值和指标值的线性关系较高，验证了中低速轨道动态监测评价算法的有效性。