基于PSO-RBF神经网络的磁浮车悬浮间隙传感器非线性校正方法*

顾艳华 彭 涛 廖珍贞 张晨昊 靖永志

(1.南京信息职业技术学院通信学院，210023，南京；2.西南交通大学电气工程学院，611756，成都//第一作者,讲师)

0 序言

磁浮车悬浮间隙传感器需要实现的功能是检测悬浮电磁铁磁极表面与轨道之间的有效悬浮气隙大小。中低速磁浮列车系统中，F型轨道的检测面为A3钢材料，其一般采用电涡流式测距传感器非接触地测量悬浮间隙值。然而电涡流式测距传感器只是在较小范围内的输入输出特性近似成线性关系。磁浮控制系统间隙检测范围是 0～20 mm，一般要求间隙的检测精度为±0.4 mm，涡流传感器在如此大量程范围内具有显著的非线性特性，而若不能解决电涡流式间隙传感器的非线性问题，悬浮系统将无法获得准确的间隙值，列车电磁悬浮系统无法通过闭环控制得到稳定悬浮状态，所以间隙传感器使用时必须进行非线性校正才能满足悬浮控制系统的要求。

传感器常用的非线性校正方法很多，一般可分为软件校正和硬件校正。文献[2]通过改进的车用霍尔传感器磁场结构的方法优化传感器的非线性就是一种硬件校正方法。文献[3]针对湿度传感器易受温度影响的问题，采用基于Laguerre 多项式的湿度非线性校正和温度补偿的复合校正模型就是一种软件方法。径向基函数(Radial Basis Function，简为RBF)神经网络能以任意精度逼近任意连续函数[4]，且在许多情况下，RBF比BP神经网络性能更加优秀。本文选用RBF神经网络搭建悬浮间隙传感器输入输出非线性特性的逆特性模型，通过选择合理的神经网络结构，结合粒子群优化(Particle Swarm Optimization,简为PSO)算法对网络参数进行优化，将逆模型补偿器作为非线性校正环节引入传感器。基于悬浮间隙传感器实测样本数据的仿真试验，证明了基于PSO-RBF神经网络逆模型补偿器非线性校正方案的有效性。该方法校正后的传感器具有优秀的线性度参数，能够提高悬浮间隙检测的精确度和线性度，其校正误差在悬浮控制系统的误差要求范围之内。

1 磁浮车悬浮间隙传感器的原理与特性

磁浮车悬浮间隙传感器实质上是一种电涡流测距传感器，电涡流传感器是基于被测金属导体在高频交变磁场内的涡流效应而工作的,其工作原理如图1所示。由图1可知，悬浮间隙传感器探头线圈与被测轨道之间的间隙为δ，当线圈两端施加高频激励源时，有同频率的交流电流i1流过检测线圈，根据电磁感应定律，检测线圈周围将产生同频交变磁场φ1，被测轨道导体由于受到交变磁场的影响将在轨道表面感应出电涡流i2，根据楞次定律，轨道表面的电涡流i2又会产生交变磁场φ2，其方向与φ1方向相反[5]。检测时，悬浮间隙的变化将会引起轨道表面电涡流的变化，最终表现为线圈阻抗的变化，通过测量电路将阻抗变化转换为电信号的变化即可得到悬浮间隙值的变化，从而实现间隙值的检测。

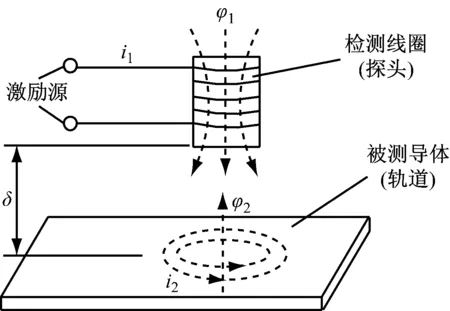
图1 悬浮间隙传感器涡流感应工作原理

电涡流传感器的检测原理和测量电路导致传感器在较大量程范围内时，其输入输出特性为非线性关系。实际的电涡流悬浮间隙传感器在0～20 mm范围内时传感器的原始静态输入输出特性曲线如图2所示。由图2可知，在气隙值较小时输出电压变化较快，而随着气隙值增大，输出电压变化缓慢，可见传感器非线性特性非常严重。

2 基于PSO-RBF神经网络的校正模型

2.1 逆模型补偿器非线性校正原理

若电涡流悬浮间隙传感器的输入输出特性用非线性函数y=f(δ)表示，其中：函数值y代表传感器原始特性输出值，函数f(*)代表传感器由输入到输出的非线性特性映射关系。传感器要实现对间隙值的检测，要求其输出y与δ之间的映射关系是单调的，则必然存在一个相应的反函数δ=f-1(y)，反函数f-1即是悬浮间隙传感器原始特性的逆特性函数。因此，可以设计一个逆模型补偿器(见图3)，将其引入到悬浮间隙传感器检测系统中即可实现悬浮间隙传感器的非线性校正功能[6]。将图3中补偿器的特性函数设为d=g(y)=f-1(y)，显然d应等于δ，即通过逆模型补偿器实现了对传感器的非线性校正。

图2 悬浮间隙传感器非线性特性曲线

图3 逆模型补偿原理框图

2.2 RBF网络模型

逆模型补偿器需要建立补偿对象的逆模型，逆模型的建立一般采用软件实现，常用的方法有查表法、多项式逼近法和神经网络人工智能建模等方法。因为径向基函数神经网络具有能以任意精度逼近任意连续函数的特性，而在各种系统建模中得到广泛应用。标准RBF神经网络的基本结构如图4所示，RBF神经网络一般由输入层节点、隐含层神经元、输出层神经元及输出权值矩阵组成[7]。

图4所示的神经网络中输入层有n个节点，隐含层具有h个径向基神经元，输出层具有m个输出层神经元。输入向量表示为x=(x1,x2,…,xn)T∈Rn，输出向量表示为y=(y1,y2,…,ym)T，φi(i=1,2,…,h)表示网络中间隐含层第i个径向基函数，ci(i=1,2,…,h)表示中间隐含层第i个基函数的数据中心，Rh×m表示连接隐层神经元和输出节点的权值矩阵，W表示输出权重矩阵,∑表示将输出层选择线性传递函数作为输出节点的神经元。

图4 RBF神经网络基本结构

常用的基函数为高斯函数：

(1)

(2)

其中，ωij是第i个隐含层神经元到第j个输出节点的权值。

一般通过最小化误差指标函数训练RBF网络，选取均方误差函数为：

(3)

其中，N代表训练样本点的个数，ej代表第j个节点的输出误差，可以表示为：

(4)

其中dj代表目标输出。

2.3 PSO算法

粒子群优化算法是一种群体智能算法，它起源于对鸟类觅食行为的研究，这种优化算法具有较强的全局优化能力并且收敛速度较快，它的缺点是在求解高维优化问题时存在容易早熟的问题。PSO算法把待求解问题的解用解空间中粒子的形式表示，每个粒子可以按照一定的速度在解空间中自由飞行，标准粒子群优化学习算法的数学模型如下式8]：

(5)

其中，vi,k和xi,k分别代表第i个粒子在第k次迭代时的速度和位置；pi,k代表第i个粒子自身在前k次迭代中适应度最高的粒子，也即是个体最优；pg,k代表所有粒子在前k次迭代中适应度最高的粒子，也即是全局最优；ω代表惯性权重，它是上一代粒子飞行速度惯性在当代粒子飞行速度中的体现，若需要粒子群具有较强的全局搜索能力则需要较大的惯性权重，当需要粒子群提高局部搜索能力时应选择较小的惯性权重；r1和r2是取值在0和1之间的独立随机数；a1和a2是加速因子，分别代表了粒子自我学习和向粒子群中优秀个体学习的能力。

3 仿真试验

3.1 试验样本数据获取

初始设计的RBF神经网是不能够正常工作的，需要采集适当的样本数据对网络进行适当训练。较多的样本数据可以更好地表现原始数据的特性，但会增大网络的训练时间；而过少的样本数据不能反应数据的原始特性，训练出来的网络泛化性会降低，因此，样本数的选择应能体现数据的特性且不宜过多。在0～20 mm全量程范围内，根据间隙值均等分布的原则选取41个数据样本点，并对其进行归一化处理以方便RBF网络计算，样本数据如图5所示。图5中，选取样本中均等分布的21个样本点作为训练样本，在网络参数优化学习时使用；选取其余20个样本点作为测试集来验证网络对陌生样本预测时的泛化性能。

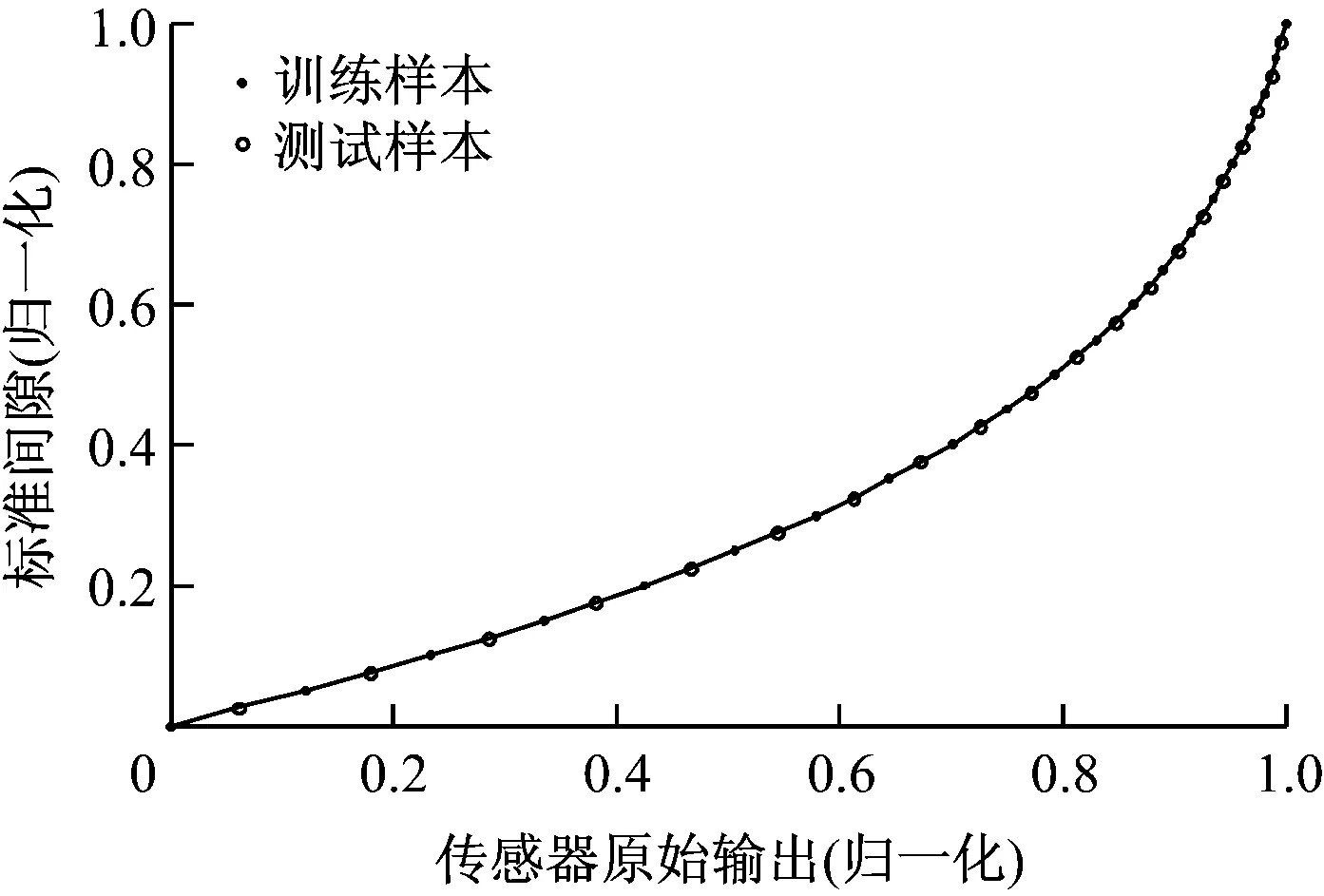
图5 数据样本归一化特性曲线

3.2 RBF神经网络参数的确定

对RBF神经网络训练的目的实际上是对RBF网络的参数寻优以找到一个多维曲面来尽可能地接近目标曲面，对于将高斯径向基函数作为隐层神经元的神经网络，需要确定的参数主要是径向基函数的个数，径向基函数的中心和宽度，以及网络的输出权值。

悬浮间隙传感器非线性校正模型为单输入单输出系统，因此其输入层和输出层均只有一个神经元。RBF神经网络的结构主要取决于隐含层神经元节点的个数，隐含层神经元的个数越多，网络的逼近能力越强，但网络也越复杂；神经元个数越少，网络越简单，但同时网络逼近能力亦随之降低。本文通过仿真试验最终选择5个隐含层神经元的网络结构。RBF网络隐含层神经元的中心值、阈值和输出权值参数的训练，采用粒子群优化算法，具体按式(6)将各优化参数用各粒子进行编码。

(6)

其中，pi表示第i个粒子；bj,i表示第i个粒子、第j个基函数中心；σj,i表示第i个粒子、第j个基函数的阈值；wj,i表示第i个粒子、第j个输出权值。将RBF神经网络误差评价指标，即式(3)所示的均方误差函数作为粒子优化适应度函数。

粒子个数的选择根据具体问题有所差别，粒子个数过少，优化效果和速度难于保证；粒子个数过多，计算量大以及相应的运算时间加长。因此，对于不太复杂的问题，粒子个数可以在20～40范围内进行选择。本文粒子个数设为30，惯性权重ω从0.9随迭代次数线性递减到0.5，a1=2.7，a2=1.3。

3.3 仿真结果与分析

最大迭代次数设为104次，误差指标设定为0.000 1，采用PSO算法对5个隐含层节点的RBF神经网络进行10次训练，将训练样本和测试样本的最大误差及优化迭代次数列于表1中，为方便分析，将每次训练由1至10进行编号。

表1 各次仿真试验结果对比

从表1可以看出，粒子群优化算法具有非常明显的随机性，每次寻优过程不同导致优化结果也不相同。由于隐含层神经元个数设置较少而误差指标要求又很高，导致PSO算法一般需要较多的迭代次数才能收敛，甚至在达到最大迭代次数时仍然没有达到误差指标。10次试验中仅第2次和第8次在限定迭代次数内达到了误差指标，其于8次在达到最大迭代次数时仍然没有得到符合误差指标的优化参数，其中第6次训练结果的误差最大。第2次、第8次和第6次训练过程的误差收敛过程如图6所示。由图6可知，3次试验在前100次迭代时误差指标均得到有效降低，在4 000次附近时第2次和第8次的误差迅速降低到了设定值10-4，而第6次实验的误差在10-4附近，此后在达到最大迭代次数之前误差指标无明显变化，这是因为此时各粒子趋近相同，失去了各相异性，以及跳出局部最优解的能力。

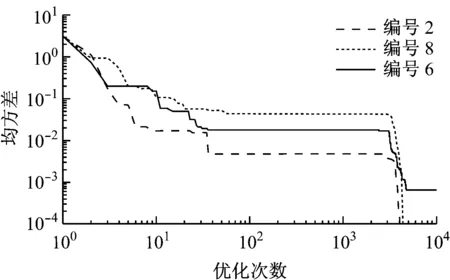
图6 各次仿真试验训练的误差收敛曲线

编号为2和8的优化迭代次数和误差较为接近。以编号2的网络为例，用训练好的网络对所有数据样本进行测试，其结果如图7所示。由图7可知，校正后的传感器特性基本为一条斜率为1的直线，表明引入RBF补偿器校正后的传感器输出与真实悬浮间隙值成严格的线性对应关系，其线性度为0.45%，表明所设计的RBF网络经PSO算法优化后实现了悬浮间隙传感器的线性校正。

图7 RBF非线性校正效果

编号2和编号8试验的校正误差如图8所示。由图8可知，训练集和测试集的最大误差分别为0.09 mm和0.10 mm，表明网络对训练样本和测试样本具有同样精准的预测效果，也验证了训练集与测试集选择的合理性和科学性。由于两个RBF网络的结构相同，均具有5个隐含层神经元，因此两次训练结果的误差分布趋势相近，而两次优化得到的网络参数不同，所以两个网络的误差分布不完全重合。但两个网络的误差曲线都表现出相同的波动特性，这与RBF神经网络的局部逼近能力有关。与某一神经元隐含层节点中心具有特定距离的样本，其校正误差较小；而其它偏离该位置的样本，其校正误差将偏大。

图8 编号2和编号8试验的校正误差

4 结语

针对电涡流式磁浮车悬浮间隙传感器在0～20 mm测量范围内输入输出严重非线性特性问题，设计了基于RBF神经网络的非线性校正补偿器。通过选择合理的网络结构，结合粒子群优化算法对神经网络各参数进行优化。基于实际传感器样本数据的仿真实验表明所设计的PSO-RBF神经网络能够高精度地逼近传感器逆模型。该种补偿方法可以有效消除非线性误差，经校正后的传感器线性度可达0.45%，全量程的检测误差小于0.1 mm，能够满足悬浮控制系统的精度要求。